洞庭湖水沙模拟的投影寻踪回归和支持向量机模型比较研究

伍小铁

（湖南省新田水文站 郴州市 425700）

李正最

（湖南省水文水资源勘测局 长沙市 410007）

洞庭湖是长江中游典型的吞吐型调蓄湖泊，随着三峡工程的建设与运行，其防洪功能已显著提高[1,2]，但与此同时其径流与输沙量关系也发生了很大变化[3,4]。为了探明洞庭湖水沙出入湖量变化和相互关系，选择合适的模拟方法非常重要。目前投影寻踪回归（PPR）[5，6]和支持向量机（SVM）模型[7,8]均已成功运用到多个专业领域，但很少有人将这两种模型进行比较。本文根据洞庭湖的系列实测水文资料，将洞庭湖径流与输沙量关系看作是一种多路水沙交互作用的复杂的小样本和非线性问题，基于PPR 和SVM 模型对洞庭湖径流与输沙量关系进行了模拟与验证，并对模拟误差进行了对比。

1 投影寻踪回归（PPR）和支持向量机（SVM）原理

1.1 投影寻踪回归（PPR）

投影寻踪是用于分析和处理非正态、非线性数据的一种新方法，其基本思想是：利用计算机技术，把高维数据通过某种组合投影到低维子空间上，并通过极小化某个投影指标，寻找出能反映原数据结构或特征的投影，以达到研究和分析高维数据的目的。投影寻踪回归模型如下：

设y=f（X）和X=（x1，x2，…，xp）分别为一维和p维随机变量，为了客观反映高维非线性数据结构特征，投影寻踪回归采用一系列岭函数的“和”去逼近回归函数，即：

式中：Gm（Zm）为第m 个岭函数；M 为岭函数的个数；Zm=aTmX 为岭函数的自变量，它是p 维随机变量X 在am方向上的投影；am为投影方向。

投影寻踪回归模型仍然采用最小二乘法作为极小化判别准则，即以式（1）中的参数amj、Gm和岭函数个数M 的适当组合，使下式

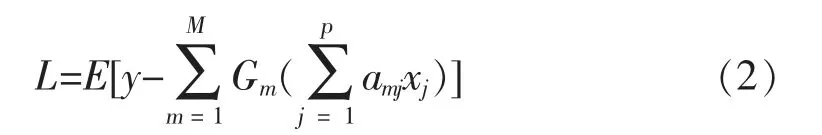
达到极小。

当前，建立投影寻踪回归模型一般均采用Friedman 和Stuetzle 提出的多重平滑回归技术方法。设非线性系统的数学模型为：

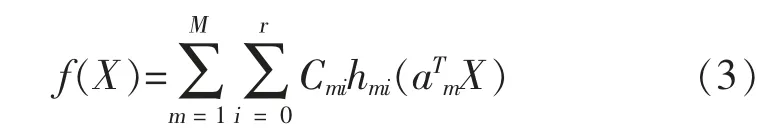
式中：r 为多项式的阶数，C 为多项式系数，hm表示正交的契比雪夫多项式，采用递推形式计算：

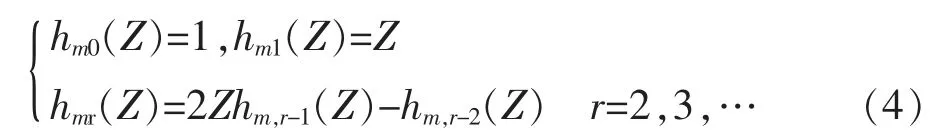
根据样本值估计式（2）中的参数，确定回归函数f（X）进行回归预测。对于式（1）中的非线性系统模型，实现投影寻踪回归的步骤如下：

step1：确定岭函数的个数M。

step2：选择M 个彼此正交的投影方向a1，a2，…，aM，建立初步回归模型：

step3：分组优化。即将amj（j=1，2，…，p）和Gm[即hmi（i=0，1，…，r）]划为一组，m=1，2，…，M，共有M组。除去其中一组外，对另外的M-1 组用step2 中得到的值作为初值，对留下的一组参数寻优。求得结果后。把这一组参数的极值点作为初值，另选一组参数寻优，反复多次直到最后选取的一组参数值，使式（1）不再减小为止。

step4：参数处理，并输出回归模型：

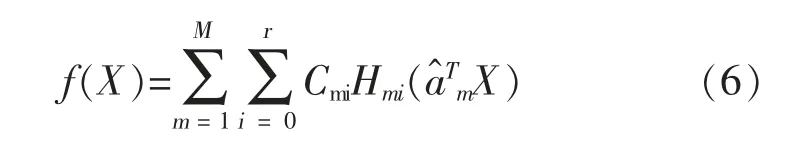
1.2 支持向量机（SVM）回归

支持向量机的基本思想是用少数支持向量代表整个样本集，本质上是通过某一事先选择好的非线性函数φ（·）将训练集数据X 映射到一个高维线性特征空间H，在这个维数可能为无穷大的线性空间中按结构风险最小化原理构造最优分类面。并利用原空间的核函数取代了高维特征空间ω 和Φ（x）的点积运算，从而避免了复杂的点积计算。对于给定的样本数据集{（xi，yi）|i=1，2，…，l} ，其中xi为输入值，yi为预测值。要求拟合的函数形式为：

根据结构风险化最小原则即要寻求最优回归超平面使：

式中：C 为调节训练误差和模型复杂度之间折中的正则化常数； ε 为不灵敏损失函数。则支持向量机的回归问题就等价于解决一个二次规划问题。最优化问题为：

SVM 用来估计回归函数时，常分为线性和非线性拟合回归两类。由上式可求得线性回归函数为：

对于非线性的情况，引入核函数即可。此时求得的是非线性回归函数为：

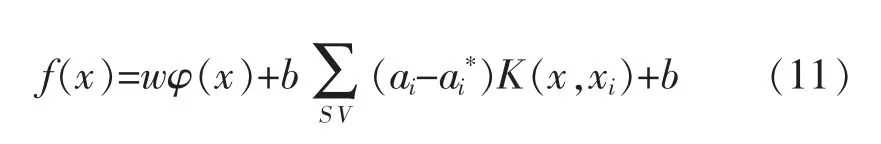
其中K（x，xi）=φ（x）φ（xi）称为核函数。核函数的选择必须满足Mercer 条件，常见的核函数有：

（1）多项式核函数。

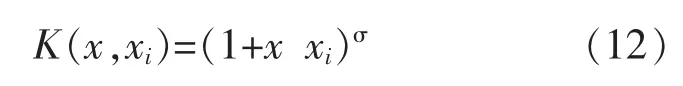
此时的SVM 是一个σ 阶多项式分类器。

（2）径向基函数。

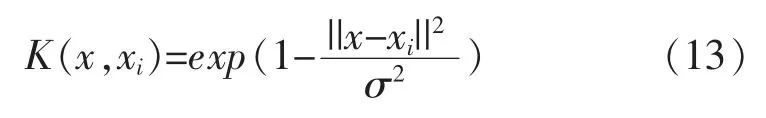
此时的SVM 是一种径向集函数分类器。

（3）Sigmoid 核函数。

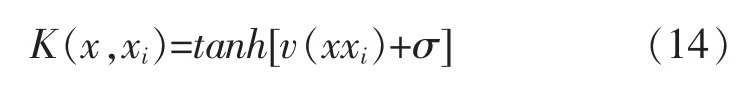
此时的SVM 是一个单隐层感知器神经网络。

目前最常见的支持向量机是Suykens J.A.K 于1999年提出了最小二乘支持向量机，采用二次规划方法代替传统的支持向量机来解决函数估计问题。最小二乘支持向量机在利用结构风险原则时，在优化目标中选取了不同的损失函数。核函数参数σ 和最小二乘支持向量机参数的取值对模型的推广预测能力有很大的影响，若取值不当，均会增大模型误差，其取值通常是采用试算法或经验法，本文采用混沌优化算法对峰值识别最小二乘支持向量机模型的参数σ、C 进行优化选取。

2 洞庭湖水沙模拟与比较分析

2.1 研究区概况与数据来源

洞庭湖位于湖南北部、长江荆江南岸，跨越湘鄂两省。北面有松滋、太平、藕池和调弦口（于1958年封堵），分泻长江水沙，南有湘、资、沅、澧四水汇入，周边汩罗江、新墙河等中小河流直接入湖，经洞庭湖调蓄，于城陵矶汇入长江，是长江中下游重要的调蓄型湖泊，对分泻荆江洪水和保障下游径流供给起着十分显著的作用，洞庭湖河网水系结构见图1。新中国成立以来，长江中游河段经历了调弦口封堵、下荆江系统裁弯取直、葛洲坝和三峡水库建成发电等；湖南省湘、资、沅、澧四水流域包括柘溪、五强溪等干流骨干性工程在内的13 000 多座各种水利工程和水土保持工程，但是一些工程并没有取得预期效果，如下荆江裁弯工程等[9]。

本研究的水文泥沙数据来源于洞庭湖区水文年鉴和主要水文站监测资料。

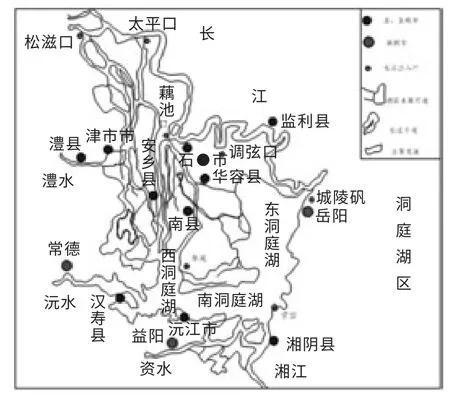
图1 洞庭湖区河网水系结构

2.2 模型整体结构

洞庭湖水沙系统具有十分明显的非线性特征，因此在建模的具体手段上分别选用投影寻踪回归和支持向量机两种方法。用1956～2004年洞庭湖区水沙序列进行模型拟合，以2005～2008年洞庭湖区水沙序列进行模型检验。洞庭湖出口城陵矶站的径流量和输沙量可简单地表述为以下非线性结构，即：

式中：Qd为城陵矶出口断面的径流量；Sd为城陵矶出口断面的泥沙；Qu为四水入流量；Su为四水来沙量；Qλ为三口分流量；Sλ三口分沙量，q 为区间产水量；V 为洞庭湖调蓄量；X地形为洞庭湖区地形特性；φ（·）为水量交换作用函数，Ψ（·）为水沙交互作用函数。

由于洞庭湖区域水下地形变化较大，加之城陵矶以上区域尚有3.96×104km2无水文站网控制，区间产水产沙量尚存在很大的不确定性。因此在建模时不宜直接涉及区间产流产沙和调蓄变化的计算。综合考虑洞庭湖河网结构的特点和水文资料获取的可能性，水沙交互模型的具体输入输出处理如下：

（1）以荆江三口新江口、沙道观、弥砣寺、管家铺、康家岗5 个水文站和湘、资、沅、澧四水的湘潭、桃江、桃源、石门4 个控制站的径流作为系统输入，以城陵矶站径流作为系统输出，建立洞庭湖水量交换模型；

（2）以荆江三口新江口、沙道观、弥砣寺、管家铺、康家岗5 个水文站和湘、资、沅、澧四水的湘潭、桃江、桃源、石门4 个控制站的径流和泥沙，以及洞庭湖水量交换模型的输出作为系统输入，以城陵矶站泥沙作为系统输出，建立洞庭湖水沙交互模型。

2.3 模拟与预测误差

按照建模序列和检验序列，分别统计两种模型的最大误差和绝对平均误差。因检验序列过短不宜独立计算误差标准差，故按建模序列和检验序列合并计算。主要误差指标计算公式如下：

式中：ei为第i 个样本的拟合（预报）误差；yi为第i 个样本实测值；yi为第i 个样本拟合或预测值；emax为最大拟合或预报误差；max（·）为取大运算符；ABS（·）为绝对值运算符；emean为平均绝对误差；Se为误差标准差；n 为样本总数。

对上述建立的二种模型分别进行回顾检验和外推预报，以式（17）计算相对误差，误差分布情况见图2。对于所建立的二种模型，用城陵矶站年径流和年输沙量按式（17）～（20）统计误差，计算结果见图3。

2.4 结果比较分析

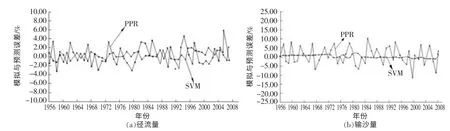
图2 洞庭湖径流与输沙量关系模型拟合与检验误差分布

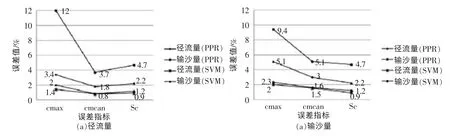
图3 洞庭湖径流与输沙量关系拟合与检验误差统计

从图2 和图3 可以看出，所建立的两种模型均具备一定的复杂系统仿真能力。而就模型的类别而言，以SVM 模型的精度较高，PPR 略低；就模型的输出物理量而言，两种模型的径流量模拟输出精度均高于输沙量，说明江湖水沙演化中输沙量的影响因素更为广泛，演化机制更为复杂，非线性特征更为显著；就模型的推广和泛化能力而言，PPR 检验序列精度对建模序列精度有所下降，SVM 检验序列精度基本与建模序列相匹配，没有表现出明显的下降趋势。可见SVM 的有效性和可信性较好，其系统数据与模型数据之间具有较好的一致性，因而其对复杂水网水沙交互作用的拟合和推广能力较强。因此，运用SVM 模型模拟计算的洞庭湖水沙出入湖量和区域泥沙淤积情况，可供江湖治理决策参考。

3 结 语

本文利用洞庭湖近50年来的水文观测资料，基于投影寻踪回归和支持向量机分别建立了洞庭湖径流与输沙量两种非线性仿真模型，得到以下结论：

（1）通过两种模型的误差比较，SVM 模型的精度较高，说明SVM 模拟和预测的结果与实测值吻合度高，试用、可操作性强，为复杂水网区的水沙分析提供了一种新方法。

（2）支持向量机的推广性能与模型的参数选择有很大关系。因此，如何根据训练样本选择合适的模型参数，以保证建立好的模型有很好的推广性能，成为设计支持向量机关键一步。

（3）通过模拟可以看出，两种模型中洞庭湖的径流量输出精度均高于输沙量，说明洞庭湖输沙量变化涉及因素更多，而不仅仅与径流量有关。影响输沙量因素，有待进一步研究。

[1] 穆锦斌，张小峰. 荆江-洞庭湖水沙变化影响分析[J]. 水利水运工程学报，2011，（1）: 84-91.

[2] 李景保，代勇，欧朝敏，等. 长江三峡水库蓄水运用对洞庭湖水沙特性的影响[J]. 水土保持学报，2011，25（3）: 215-219.

[3] 马元旭，来红州. 荆江与洞庭湖区近50年水沙变化的研究[J].水土保持研究，2005，12（4）: 103-106.

[4] 毛北平，梅军亚，张金辉，等. 洞庭湖三口洪道水沙输移变化分析[J]. 人民长江，2010，（2）: 38-42.

[5] FRIEDMAN,J.H.，TUKEY，J.W. A projection pursuit algorithm or exploratory data analysis [J]. IEEE Transactions on Computer，1974，23（9）: 881-890.

[6] 王顺久，侯玉，张欣莉，等. 流域水资源承载能力的综合评价方法[J]. 水利学报，2003，（1）: 88-92.

[7] VAPNIK，V.N. The nature of statistic learning theory[M].New York:Spring Verlag，1995.

[8] 李正最，谢悦波. 基于支持向量机的洞庭湖区域水沙模拟[J]. 水文，2010，30（2）: 44-49.

[9] 潘庆燊. 下荆江人工裁弯30年[J]. 人民长江，2001，32（5）:27-29.