“知道者悖论”解析

张 莹，雒自新

(1.西安电子科技大学外国语学院，西安 710071;2.西安交通大学人文社会科学学院，西安 710049)

悖论问题是困扰人类心智千年的难题。有的哲学家甚至认为整个一部哲学史可以看作是与各种悖论做斗争的历史。在为数众多的悖论当中最著名当数说谎者悖论，这不仅因为它具有十分悠久的历史，更是因为该悖论以最为简单的形式告诉人们，通常对“真”这一我们日常生活中普遍使用的概念的直觉理解是包含矛盾的。考虑语句(L):L是假的。那么L这句话是真的还是假的呢?如果L为真，那么它说的是自己为假，因而它为假;如果L为假，那么说它自身为假是假的，因此它又为真。这显然是矛盾的，但我们又找不出问题究竟出在哪里。语句L被称为“说谎者语句”，“说谎者悖论”这一名称由此而来。

对说谎者悖论的探讨已经持续了两千多年，但遗憾的是至今仍没有就该悖论的解决意见达成一致。值得注意的是进入20世纪中后期以来，一类型新的悖论走进了研究者们的视线，并逐渐得到了逻辑学家与哲学家们的重视，这就是知道者悖论。在持续多年的研究过程中，该悖论多层面的理论意义与学术价值逐步得以彰显［1］。与说谎者悖论类似，知道者悖论当中也涉及类似的语句，即所谓知道者语句(K):认知主体i知道K为假，该悖论由此而得名。然而，许多学者对“知道者悖论”(Knower Paradox)这一概念所指称的对象却并不清楚，甚至与其简化形式或者其前身——绞刑悖论——相混淆。另外，在道义逻辑中也有所谓知道者悖论。因此，澄清“知道者悖论”这一概念就显得非常必要。

一、知道者悖论的前身

知道者悖论的起源可以追溯到20世纪40年代在欧洲民间流传的“突然演习问题”。在持续多年的研究中，“突然演习问题”逐渐演变为一个著名的哲学问题——“绞刑悖论”。也就是说，知道者悖论来源于其前身——绞刑悖论，但与该前身却并不完全相同。

绞刑悖论描述的是如下场景:法官向一名罪犯宣判，他被判处绞刑，而且该罪犯将在从宣判之日的第二天起的10天中的某一天被执行绞刑，但这次绞刑是一次令罪犯出乎意料的绞刑，意思是说，在执行绞刑的前一天晚上，罪犯不会知道绞刑将在第二天执行。这看似一则很正常的宣判，然而当这名聪明的罪犯听到该宣判时，心中一阵窃喜:按照该宣判，自己不会被执行绞刑。为什么呢?该罪犯的如意算盘是这样的:根据法官的宣判，绞刑不可能在这10天中的最后一天执行，这是因为如果在最后一天执行，那么由于前9天都没有执行绞刑，所以在倒数第二天(也就是第9天)晚上，我就会知道第二天(也就是最后一天)将执行绞刑，但这不满足法官所宣判的这次绞刑的“意外性”，因而绞刑不可能在最后一天执行。绞刑也不可能在倒数第二天执行，因为如果在倒数第二天执行，那么由于前8天都没有执行绞刑，而前面的推理已经排除了绞刑在最后一天执行的可能性，所以在倒数第三天(也就是第8天)晚上，我就会知道第二天(也就是倒数第二天)将执行绞刑，这再一次不满足法官所宣判的绞刑的“意外性”，因而绞刑不可能在倒数第二天执行。按照同样的思路进行推理，可以依次排除绞刑在倒数第三天、倒数第四天……执行。于是该罪犯断定法官的宣判是不可实现的。然而，法官就在接下来的第四天突然来到该罪犯面前对他执行了绞刑，这大大出乎该罪犯的意料，从而不折不扣地实现了之前的宣判。可悲的是，该罪犯到死都没有明白为什么自己无懈可击的推理当中却包含着矛盾。

前面，我们以非形式的方式叙述了绞刑悖论。尽管该悖论还有诸多实质相同的其他版本，比如克里普克(S.A Kripke)［2］宁愿称之为“意外考试悖论”，但我们还是遵循蒯因(W.V.Quine)的称谓将之称为“绞刑悖论”。经过奥康纳(D.O’Connor)［3］、斯克利文(M.Scriven)［4］、蒯因［5］、沙乌(R.Shaw)［6］、蒙塔古(R.Montague)和卡普兰(D.Kaplan)等哲学家与逻辑学家的深入研究与整理，前述非形式叙述的绞刑悖论已经发展成一个关于“知识”概念的严格的自指悖论。

从前述非形式叙述不难看出，绞刑悖论中绞刑不可能执行的推导与天数无关。因此，在这里为简洁明了起见，只考虑有两个可选择日子的情形，这不会影响问题的实质。如果用p代表罪犯，F代表“绞刑发生在第一天”，S代表“绞刑发生在第二天”，f表示第一天，z表示宣判的当天，A代表法官的判决。Ki(x)解释为“认知主体i知道x”。符号I(s，t)是一种缩写，它表示“从s可以合乎逻辑地推导出t”。则法官的宣判的严格形式如下(其中(「﹁A⏋表示语句﹁A的标准名称的哥德尔数):

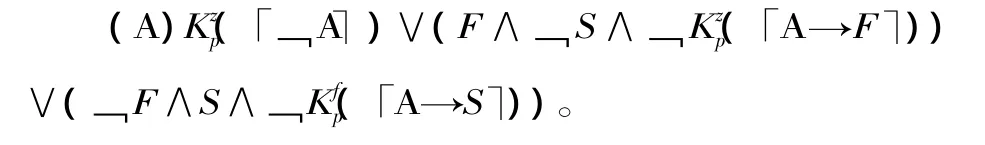
绞刑悖论所描述的情境(也就是推导出矛盾所使用的前提)的严格形式如下:

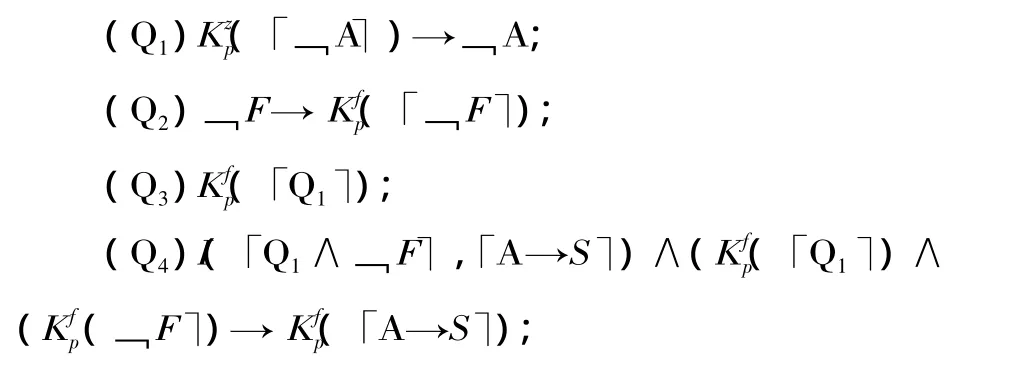
在以上8条前提中，Q1表示“如果罪犯在宣判之日知道﹁A，那么﹁A为真”，即“知识蕴含真理”原则，这是最基本的认知规则。Q4、Q6与Q8表达的则是知识的演绎封闭性。Q2、Q3、Q5与Q7表达罪犯作为正常的具有起码理性的认知主体所具有的基本认知与记忆能力，例如Q2表示“如果绞刑在第一天没有执行，那么罪犯在第一天知道这一点”。

法官的宣判A可以经由哥德尔自指定理在扩充的形式算术系统当中得到表达，即是扩充的形式算术系统当中的一条定理。在形式算术系统当中经过严格的逻辑推理，既可以推出A，即宣判必定能实现;又可以推出﹁A，即宣判不能实现(具体推导过程详见参考文献［7］，本文限于篇幅略去)。于是，矛盾就产生了。

矛盾的产生表明，Q1～Q8这组前提假设与“初等语法”(即形式算术)原则是不相容的。也就是说，如果我承认这组前提假设是合理的，并且与此同时也承认“初等语法”的合理性，那么一个货真价实的逻辑悖论就产生了。这就是知道者悖论的前身——绞刑悖论。这个悖论的重要性恰恰“来自于这些假定的直觉合理性。无疑地，在发现这个悖论之前，人们也肯定会有把体现在Q1～Q8中的认识论原则充分形式化的要求，这即使不是必需的，至少不是不可能的”［7］89。

二、知道者悖论的严格刻画

前述绞刑悖论严格的形式刻画是由蒙塔古和卡普兰在其1960年发表的文章中给出的［7］，他们认为该悖论的出现必将会引出哲学认识论上的某些新探讨，因此他们在给出这种刻画之后，对该问题进行了进一步深入的思考。蒙塔古和卡普兰发现，可以考虑一个从该悖论引申出来的更简单的结果，这样就会使问题变得更加尖锐。如前所述，绞刑悖论中绞刑不可能执行的推导与天数无关。也就是说，即使只考虑一个而不是两个可能的执行绞刑日期，仍然可以得到一个严格的悖论。在这种情形下法官的宣判为如下形式:“除非罪犯在宣判之日晚上知道本宣判为假，否则下述要求将被满足:绞刑在接下来的一天执行，而罪犯在宣判之日晚上不知道基于本宣判‘绞刑在接下来的一天执行’为真。”

实际上，可以沿着这条思路继续进行下去，执行绞刑的可能日期的数目可以进一步缩减至零。此时法官的“宣判”只是断言下面这个唯一的要求将被满足:“罪犯在宣判之日晚上知道本宣判为假。”该“宣判”可以用如下公式表达:

在皮亚诺算术系统(或者与之等价的鲁滨逊算术系统)当中引入一个一元谓词Ki(x)(对该谓词的解释如前)，并且引入与Q1、Q3和Q4类似的表达认识论规律的一般规则作为定理:

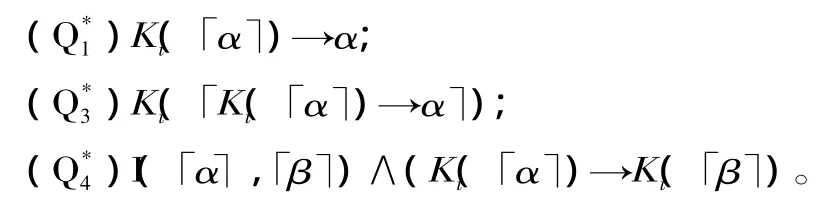
由哥德尔自指定理得，下述表达法官的宣判的公式是该形式系统中的定理:

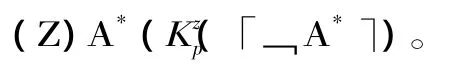
由此所得到的系统记作T，在T中可作如下演绎推导:

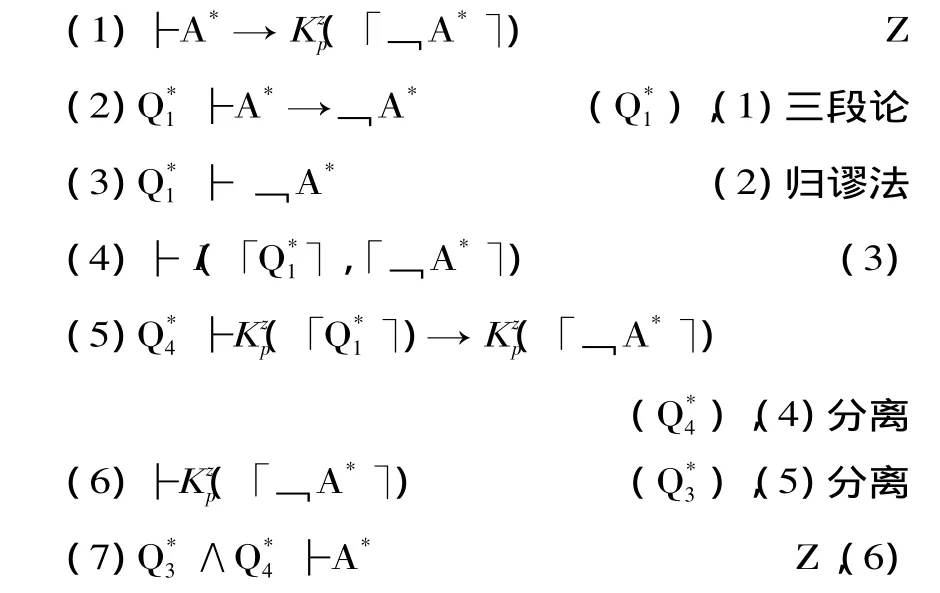
在上述推导当中，式(3)得到了﹁A*，而(7)得到了A*，这显然是矛盾的。语句A*是说，其自身的否定为认知主体p所知道。这与著名的说谎者语句(即“本语句为假”)的形式十分类似，因而可以将语句A*称为“知道者语句”。

三、简化的知道者悖论

在多年的研究当中，知道者悖论有时候也以它的简化形式出现。从以上知道者悖论的严格形式刻画的过程中不难看出，哥德尔自指定理起到了至关重要的作用，因为该定理使得法官的宣判这一自指语句经符号表达之后成为形式算术系统的一条定理。稍加分析可知，由哥德尔自指定理所得，与前述(Z)类似的同样是皮亚诺算术系统或者鲁滨逊算术系统的定理。在以上解释之下，语句A＊＊的意思是:认知主体p不知道A＊＊。相比之下，语句A＊＊在结构上比前面的语句A*更接近于“说谎者语句”L:L↔﹁T(「L⏋)。如果把知道者语句构造为A＊＊，则稍加修改认知规则以及推导建构所依赖的形式系统，就可以构造出知道者悖论的另一个简化版本(相应地，前面提到的可以称之为知道者悖论的经典版本)。

同理，在皮亚诺算术系统或者鲁滨逊算术系统中添加一个被解释为“认知主体i知道哥德尔数为x的语句”的一元谓词Ki(x)。把如下表达认知规则的公式和推理规则分别作为公理和推导规则引入该系统:

由此所得到的系统记作T*，在T*中可作如下演绎推导:

显然，式(3)和(5)矛盾，于是悖论得以建构。在许多对知道者悖论的研究文献当中，所针对的实际上是知道者悖论的该简化形式，可以称之为“简化的知道者悖论”。

四、道义逻辑中的知道者悖论

值得注意的是，在相关文献中还有一类所谓的“知道者悖论”——“道义逻辑中的知道者悖论”(the paradox knower in deontic logic)。所谓“道义逻辑”(Denotic Logic)也称规范逻辑，是研究“应该”“允许”“禁止”等概念的广义模态逻辑的分支之一。道义逻辑中的知道者悖论如下，考察下面 3 个语句［8］:

(I)在赵六看守仓库期间王五在仓库放火。

(II)如果在赵六看守仓库期间王五在仓库放火，那么赵六应该知道这件事。

(III)王五不应该在仓库放火。

这3个语句看起来都很正常，并没有什么特别之处，而且我们也能够理解它们的意思。然而，如果以它们为前提，再加上如下两条规则，就可以推导出矛盾:

(D)被应该的东西蕴含的东西也是应该的。

(V)赵六知道王五在仓库防火“蕴含”王五在仓库放火。

由(IV)、(V)和规则(D)得:

(VI)王五应该在仓库放火。

这样，(III)和(VI)矛盾。

矛盾的导出所依赖的前提包括:表达事实的语句(I)、符合直觉的道义语句(II)和(III)、基本道义规则“被应该的东西所蕴含的东西也是应该的”、认知规则，以及经典逻辑中的分离规则。这些前提均为具有“道义思维”的认知共同体所普遍接受。这就是所谓“道义逻辑中的知道者悖论”。从以上推导过程不难看出，如果没有认知规则，就得不出(V)，而若没有(V)就无法应用道义规则(D)，也就不可能得到(VI)。也就是说在这里的矛盾的导出中起到了至关重要的作用，“道义逻辑中的知道者悖论”由此而得名。

五、结论

知道者悖论是关于“知道”的严格意义的逻辑悖论。所谓严格意义的逻辑悖论“指谓这样一种理论事实或状况，在某些公认正确的背景知识之下，可以合乎逻辑地建立两个矛盾语句相互推出的矛盾等价式”［9］。由于该悖论以最为简单的形式告诉人们，通常对“知道”这一概念的理解是包含矛盾的，所以知道者悖论得到了来自任何关注知识概念的学科的广泛重视。尤其是进入21世纪以来，知道者悖论研究取得了迅速发展［10］。

与经典版本相比，在简化的知道者悖论当中，矛盾的导出并没有用到认知规则而是代之以推理规则(NK)。但显然，在系统T*中，从公理和(NK)出发可以推导出和

在道义逻辑中的知道者悖论当中，矛盾的导出本质地涉及到了认知规则(Q*1)，因而与知道者悖论及其简化形式与前身有着十分密切的联系。但很显然，两者之间也存在着本质上的不同:道义逻辑中的知道者悖论还本质地涉及到了基本道义规则，因而是一个比知道者悖论更为复杂的问题。

综上所述，在不同的情境当中，由于背景知识的不同，“知道者悖论”(Knower Paradox)这一概念与4个悖论相关。因此，对知道者悖论进行研究，首先应该明确这4个悖论之间的联系与区别。

［1］雒自新.知道者悖论及其价值［J］.科学技术哲学研究，2010(4):46-49.

［2］Kripke S A.On Two Paradoxes of Knowledge［C］//Philosophical Troubles:Collected Papers.Oxford:Oxford U-niversity Press，2011:27.

［3］O’Connor D.Pragmatic Paradoxes［J］.Mind，1948(57):358-359.

［4］Scriven M.Paradoxical Announcement［J］.Mind，1951(60):403-407.

［5］Quine W V.On a So-Called Paradox［J］.Mind，1953(62):65-67.

［6］Shaw R.The Paradox of the Unexpected Examination［J］.Mind，1958(67):382-384.

［7］Montague R，Kaplan D.A Paradox Regained［J］.Notre Dame Journal of Formal Logic，1960(1):79-87.

［8］Feldman F.The Paradox of the Knower［J］.Philosophical Studies，1989(55):93-100.

［9］张建军.逻辑悖论研究引论:修订［M］.北京:人民出版社，2014:7.

［10］雒自新.“知道者悖论”研究新进展述评［J］.哲学动态，2009(7):81-85.