基于分类分析的集装箱码头泊位分配研究

杨露，余丽婷，陆克斌

全球超过80%以上的货物都是通过水路运输，现代港口成为国际供应链的重要环节。泊位作为重要的港口资源，其建设投资巨大，一旦集装箱码头建成就很难更改泊位位置，所以合理的集装箱码头泊位分配至关重要。合理的泊位分配可减少单船在港时间和所有船次在港总时间，提高集装箱码头作业效率。

国内外学者对码头泊位分配进行了很多研究。孙少文等［1］建立船舶总在港时间最小的离散泊位分配模型，对潮汐运动影响下的靠泊计划进行分析。杨斌等［2］建立以最小化船舶总的加权作业时间为目标的混合整数规划模型，研究船舶优先权的离散泊位优化调度问题。王致远等［3］建立基于低碳经济下的泊位—岸桥分配模型研究泊位分配以及港口的岸桥分配问题。乐美龙等［4］研究中转港班轮运输背景下的泊位分配和子箱区指派联合计划问题。彭建良等［5］构建群岛泊位分配问题模型，结合混合粒子群算法求解，期望实现船舶总在港时间最小化的目标。张恒等［6］建立了双港泊位分配协同优化模型，该模型不仅能够进一步优化两港总的延误时间，而且能够明显减少船舶燃油消耗量。Ji Ming Jun等［7］建立评价指标体系并采用Monte Carlo模拟解决连续泊位分配问题。C.Bierwirth等［8］采用分类技术研究泊位分配及岸桥调度问题。Yan Shang Yao等［9］采用网络建模方法解决动态泊位分配问题。M.M.Rodriguez等［10］基于鲁棒性研究泊位分配及岸桥调度问题。Pang King Wah等［11］采用整数规划模型和迭代分解启发式方法解决泊位分配问题。T.Robenek等［12］采用混合整数规划方法解决港口泊位分配及岸桥分配问题。Hu Qing Mi等［13］采用多目标混合整数规划模型解决泊位和岸桥调度问题。Lin Shi Wei等［14］采用模拟退火算法（SA）解决泊位分配问题。Gao Zhi Jun等［15］采用遗传算法使停泊时间最小化来解决泊位分配问题。

以上研究基本上是从泊位分配问题的角度出发，未对泊位分配过程中产生的大量历史数据进行分析。然而对于集装箱码头泊位分配而言，大量的历史数据具有很大的研究价值。因此，笔者将采用数据挖掘分类技术中的ID3方法对集装箱码头泊位分配的历史数据进行分析，挖掘得出泊位分配分类规则，将此分类规则应用于泊位分配中，据此得到泊位分配新策略，起到改进码头经济效益的作用。

一、问题描述

集装箱码头泊位分配，就是为到港的船舶分配预靠泊位，供其卸货、装货作业，以减少单船在港时间和在港总时间，提高集装箱码头生产效率，从而使港口利润最大化。

在泊位分配众多的影响因素中，有些因素对泊位分配是随机性的，并无规律可循，也无直接的意义，所以并不列入因素选取范围。然而针对一些对泊位分配过程中起到重要影响的因素要加以分析，确定是否列入选取因素。基于以上选取原则，最终选取的因素如下：（1）码头岸壁线总长度；（2）岸桥数目；（3） 船舶船长；（4）服务时间；（5）集装箱箱量。

有别于其他泊位分配问题，笔者基于数据挖掘技术，采取泊位分配模型，通过分析船舶靠泊是准时还是延时，结合上述考虑的因素作为船舶属性，最终得到泊位分配分类规则，达到预期设想的效果。即，如果泊位分配得当，可提高泊位运作的效率，减少船舶在港时间，尽可能增加经济效益。

二、泊位分配模型建立

（一）模型选取

总结前面的问题描述，将连续泊位靠泊计划数学模型选取如下：

（1）按照25 m为一个小单位，将集装箱码头岸线长度划分为若干个小单位的泊位。

（2）对于每一艘靠泊的船舶，将其船长乘以靠泊安全距离系数后，也按照25 m为一个单位，将集装箱船长折算为该单位的整数倍。

（3）只有在空闲连续泊位的长度大于船长时，该船才能按照优先级原则进行靠泊装卸作业。

（4）对于船长不超过150 m的船舶，根据集装箱箱量，分配给该船的岸桥数量不超过3个。

（5）对于船长超过150 m的船舶，根据集装箱箱量，分配给该船的岸桥数量不超过4个。

（6）设定每个岸桥每小时的平均装卸速度为40个TEU。

（7）设定码头岸线上的岸桥总数量为18台，此数据可以根据集装箱港口码头的实际岸桥数量进行更改。

（二）模型假设

对该数学模型的假设如下：

（1）任何一艘船舶在抵港之后，都不会因为等待时间过长，而在没有靠港之前，出现驶离港口的现象。

（2）不存在船舶为了节省码头操作费而不充分利用空闲岸桥数量的现象。

（3）任何船舶，在靠港、集装箱装卸作业完成之后，不允许出现在港逗留而不立刻驶离港口的现象。

（4）对于同时抵港的集装箱船舶，即靠泊优先级相同的船舶来说，本数学模型会通过对其随机选择来重新安排各自的优先级进行靠泊。

（5）为了达到连续泊位靠泊计划更好的比较效果，这里为每艘船上分配3台岸桥。

三、数据获取

（一）数据准备

笔者选取某集装箱码头一段时间内的泊位分配作为实际研究案例，以此集装箱码头此段时期内的进港船舶预期船期、装卸量等数据作为研究对象，数据来源于该码头的数据库。

该数据库中各主要数据表的基本结构如下：（1）船舶基本信息表，其中包括主要的数据内容有船号、船名、船长、层数、贝数、排数；（2）船舶装卸量信息表，其中包括主要的数据内容有船号、船名、进口箱量、出口箱量；（3）船舶停靠信息表，其中包括主要的数据内容有船号、船名、到港标志、出发港、靠泊时间、离泊时间、泊位、卸货开始时间、卸货结束时间、装货开始时间、装货结束时间；（4）岸桥分配信息表，其中包括主要的数据内容有船名、预靠泊位、岸桥数。

根据选取的因素进行数据选取，对多表进行连接，得到了与泊位分配数据挖掘相关的信息数据表，其内容包括如下：船号、船长、箱量、靠泊时间、等待时间、开始作业时间、离泊时间、计划离泊时间、延迟离泊时间、泊位，岸桥数。各数据表之间的关系如图1所示。

图1 数据表关系图

（二）数据选取

对数据库中的四个表中数据进行选取，得到用于数据挖掘的信息数据表。现列举信息数据表中部分数据如表1：

（三）数据预处理

本问题已经将1 000 m长的码头岸线划分为40个25 m长的小单位泊位。为了更好地根据船舶的长度来分配相应数量的泊位长度，下面先将船长在乘以靠泊安全距离系数之后，化成25 m的整数倍，根据表1，乘以安全系数后的船长结果如表2所示。

表2 乘以靠泊安全系数后的船长

再将船长四舍五入为25 m的整数倍，得到表3。

表3 化为25 m整数倍后的船长

这样，就可以将船长化为25 m小单位的泊位的 整数倍，每艘船所占的小泊位数量如表4所示。

表4 每艘船所占的25 m小泊位个数

根据表1、表2、表3，再根据已知的船长和表4中每艘船所占的泊位，就可以得出具体每艘船所占的泊位位置。因岸桥每小时平均装卸速度为40个TEU，此泊位分配模型已假设每艘船分配3台岸桥，即每艘船每小时平均装卸速度为120个TEU，所以此处把每艘船的箱量化为其每小时装卸速度的倍数，如表5所示。

表5 每艘船相比每小时装卸速度的箱量倍数

通过表1计算每艘船的服务时间，并将服务时 间化整，计算结果如表6。

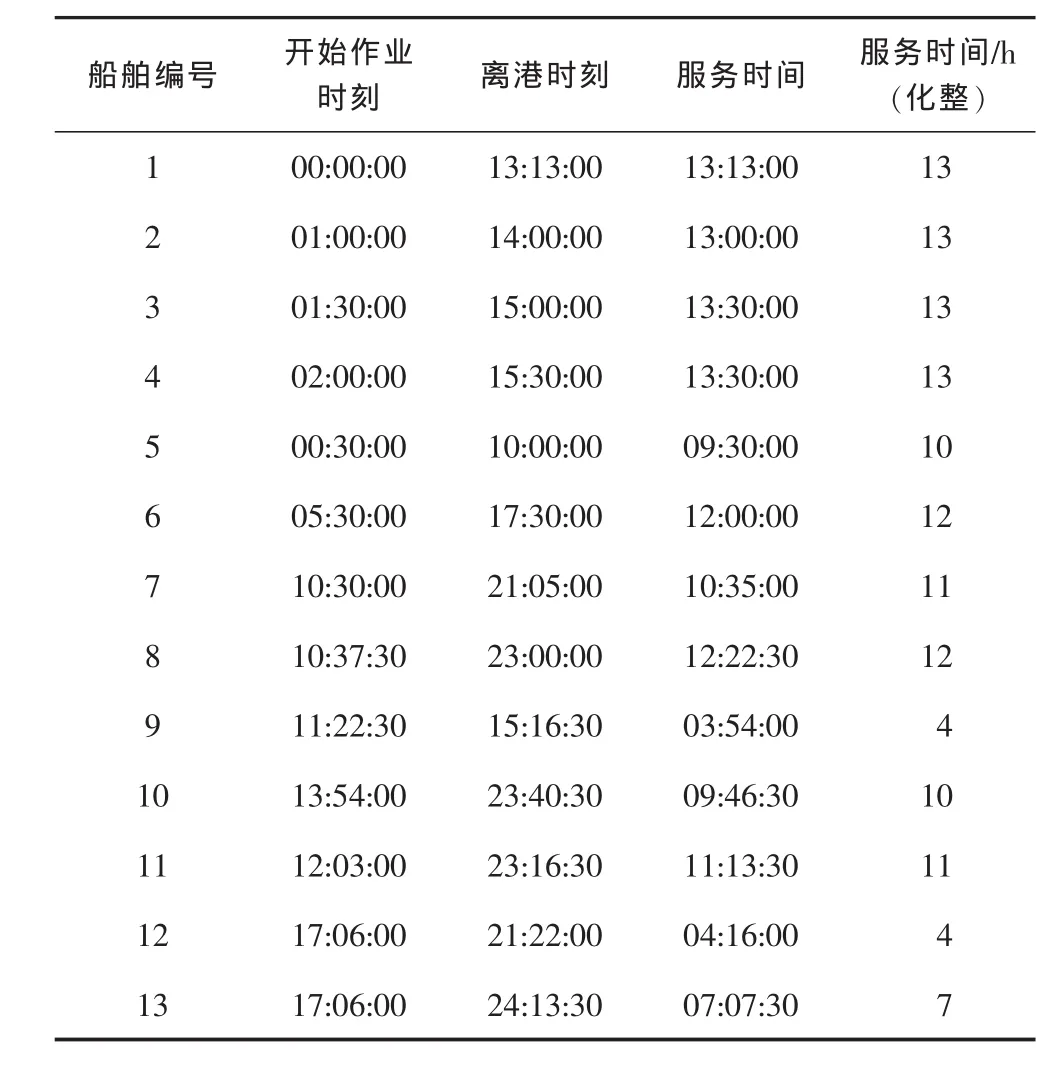
表6 每艘船的服务时间

四、基于ID3方法的泊位分配分类分析

（一）离散化信息表

用一个泊位分配实例进行说明，选取码头一天内靠泊的船舶进行分析，假设有包括5个属性和1个决策的13个样本，信息系统（IS）表如表7所示。A、B、C、D、E 表示 IS的属性，F 表示决策， 其中 F=1表示有泊位分配，F=0表示无泊位分配。在表中，假定VA=[95.7，201.3]，VB=[468，1 485]，VC=[3:54:00，13:30:00]，VD=[4，8]。

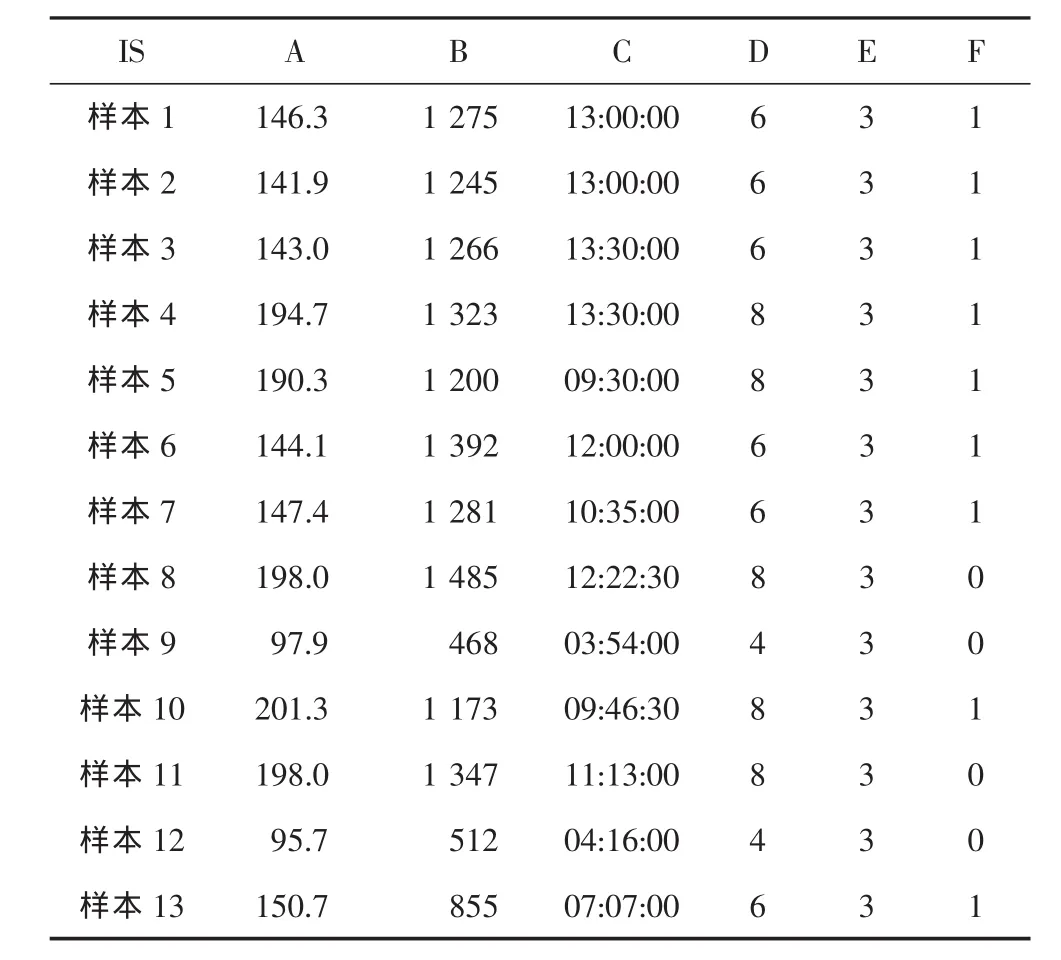
表7 信息系统（IS）初始样本

（二）简化表格

通过一些步骤，可以将表7简化为表8。

表8 新信息系统（IS）

（三）ID3方法分类分析

采用决策树中常用的ID3方法对表8进行分类分析，过程如下：

1.信息熵的计算

信息熵的计算公式为：

在实际计算中，P（ui）用类别为 ui的样本所占总样本的比例来替代，即 P（ui）=|ui|/|S|，|S|表示训练样本集中样本的总数，|ui|表示类别为ui的样本数。

对于表 8 所示的样本集，u1=“准时”，u2=“延时”，|S|=13，|u1|=9，|u2|=4，

P（u1）=，从而有

2.属性A的条件熵计算

条件熵的计算公式为：

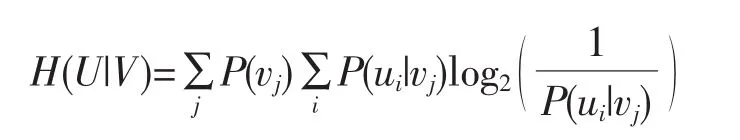
其中，P（ui|vj）表示属性 A 取值 vj时，类别 ui的条件概率，即 P（ui|vj）=|ui|/|vj|。对于表 3 到表 7 所示的样本集，A=船长，取值 v1=150 m，v2=200m，v3=100 m。在船长取值150 m的样本数有6个，取值200 m的样本数有5个，取值100 m的样本数有2个，所以有：

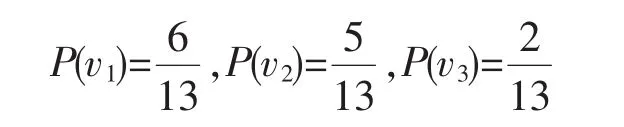
船长为150 m的6个样本中全部都准时靠泊，所以有：

P（u1|v1）=1

H（U|V）=0.393

3.属性A的互信息计算

属性A的互信息Gain（A）的计算公式为：

Gain（A）=H（U）-H（U|V）

V为属性A的所有输出状态集。

对于表8所示的训练样本集，A=船长的互信息Gain（船长），其值为：

Gain（船长）=H（U）-H（U|V）=0.890-0.373=0.517bit

类似可得：

Gain（箱量）=0.890-0.432=0.458bit

Gain（服务时间）=0.890-0.308=0.582bit

Gain（泊位）=0.890-0.373=0.517bit

4.建立决策树的根节点和分枝

ID3方法中选择互信息最大的属性即服务时间作为根节点，在13个样本中对服务时间的6个取值进行分枝。6个分枝分别对应6个子集，分别是F1={1，2，3，4}，F2={5，10}，F3={6，8}，F4={7，1}，F5={9，12}，F6={13}。其中，F1中样本的服务时间属性为13 h，F2中样本的服务时间属性为10 h，F3中样本的服务时间

同理有：属性为12h，F4中样本的服务时间属性为11h，F5中样本的服务时间属性为4h，F6中样本的服务时间属性为7h。其中，F1、F2、F6中所有样本的类别属性取值都为准时靠泊，因此对应该分枝的节点为叶子节点，并标识为准时。F5中所有样本的类别属性取值都为延时靠泊，因此对应该分枝的节点为叶子节点，并标识为延时。其余两个子集的类别属性既含有准时又含有延时，将递归调用建树算法。

5.递归调用

分别对F3和F4子集调用ID3方法，在每个子集中对余下的属性求互信息。

（1）F3中服务时间的取值全为12h，在余下的两个属性中求互信息最大的属性，即船长属性。以它为该分枝的根节点，再向下分枝。由于船长取值为100m的样本在类别属性上的取值均为准时靠泊，该分枝的节点为叶子节点，标识为准时。（2）同理，可得出F4的分类情况。

应用数据挖掘中的分类方法分析表8中的集装箱码头泊位分配数据。完整的泊位分配模型如图2所示。

根据图2分类分析泊位分配模型，最终得到如图3所示的决策树。

图2 分类分析泊位分配模型

图3 ID3决策树

（四）规则获取

根据图3得到的ID3决策树，直接提取分类规则，并以IF-THEN形式表示。对从根节点到叶节点的每一个路径都可以是一条规则。分类规则提取如下：

规则1：IF 服务时间=“13h” THEN 该船属于“准时靠泊”。

规则2：IF 服务时间=“10h” THEN 该船属于“准时靠泊”。

规则3：IF 服务时间=“12h”and 船长=“150m”THEN 该船属于“准时靠泊”。

规则4：IF 服务时间=“12h”and 船长=“200m”THEN 该船属于“延时靠泊”。

规则5：IF 服务时间=“11h”and 船长=“150m”THEN 该船属于“准时靠泊”。

规则6：IF 服务时间=“11h”and 船长=“200m”THEN 该船属于“延时靠泊”。

规则7：IF 服务时间=“4h” THEN 该船属于“延时靠泊”。

规则8：IF 服务时间=“7h” THEN 该船属于“准时靠泊”。

（五）仿真验证

笔者对集装箱码头泊位分配进行仿真系统建模，分别分析原策略和分类规则集成于仿真系统得到的泊位分配新策略，进而实现对集装箱码头泊位分配问题的优化。

使用原始数据中实际的泊位分配策略，根据泊位分配分类规则得到的新策略分配相同参数下的18条船次，比较两策略下的在港总时间。根据仿真实验，得到两种泊位分配策略情况下18船次的单船在港时间，绘制两次仿真结果的折线图，进行直观比较，如图4所示。

图4 仿真结果比较

其中，横坐标为船次；纵坐标为单船在港时间，单位为小时；蓝色的柱状为原泊位分配策略，红色的柱状为数据挖掘后的新泊位分配策略。

根据图4仿真结果比较，可以看出，应用分类规则的泊位分配策略，单船在港时间趋于稳定，且避免了一次作业用时过长的问题，可以减少集装箱码头作业的长时间等待。在此基础下，18船次在港总时间也是重新分配的情况下用时较短，节约了大约2 h的在港总时间。该结论证明本次数据挖掘得到的泊位分配分类规则为集装箱码头泊位分配提供了新策略，减少了单船在港时间和所有船次在港总时间，提高了集装箱码头生产效率。

[1]孙少文，杨斌，胡志华.潮汐影响下的港口离散泊位分配问题研究[J].合肥工业大学学报（自然科学版），2014（32）.

[2]杨斌，岳宇菲.离散泊位分配装卸量加权延迟最小化策略[J].河南科技大学学报，2014（35）.

[3]王致远，范元伟.低碳经济下港口泊位—岸桥分配问题 [J].物流科技，2015（2）.

[4]乐美龙，赵彦营.基于最优靠泊位置的泊位分配和子箱区指派联合计划[J].系统工程，2015（33）.

[5]彭建良，李仁健，李修琳.基于混合粒子群算法的群岛泊位分配问题研究[J].工业工程，2014（17）.

[6]张恒，陈秋双.考虑船舶废气排放的港口群协同泊位分配研究[J].交通运输系统工程与信息，2014（14）.

[7]Ji Ming Jun， Zhu Hui Ling， Wang Qing Bin， Zhao Rui， Yang Yong Zhi.Integrated Strategy for Berth Allocation and Crane Assignment on a Continuous Berth Using Monte Carlo Simulation[J].Simulation，2015（1）.

[8]Bierwirth C，Meisel F.A Follow-up Survey of Berth Allocation and Quay Crane Scheduling Problems in Container Terminals[J].European Journal of Operational Research，2015（3）.

[9]Yan Shang Yao， Lu Chung Cheng， Hsieh Junh Siao， Lin Han-Chun.A Network Flow Model for the Dynamic and Flexible Berth Allocation Problem[J].Computers and Industrial Engineering，2015（81）.

[10]Rodriguez M M，Salido M A，Barber F.Robust Scheduling for Berth Allocation and Quay Crane Assignment Problem[C].Mathematical Problems in Engineering，2014.

[11]Pang King Wah，Liu Ji Yin.An Integrated Model for Ship Routing with Transshipment and Berth Allocation[J].IIE Transactions，2014（12）.

[12]Robenek T，Umang N，Bierlaire M，Ropke S.A Branchand-price Algorithm to Solve the Integrated Berth Allocation and Yard Assignment Problem in Bulk Ports[J].European Journal of Operational Research， 2014（2）.

[13]Hu Qing Mi， Hu Zhi Hua， Du Yu Quan.Berth and Quaycrane Allocation Problem Considering Fuel Consumption and Emissions From Vessels[J].Computers and Industrial Engineering，2014（1）.

[14]Lin Shi Wei，Ting Ching Jun.Solving the Dynamic Berth Allocation Problem by Simulated Annealing[J].Engineering Optimization，2014（3）.

[15]Gao Zhi Jun，Cao Jin Xin，Zhao Qing Yu.Optimization Research of Berth Allocation and Quay Crane Assignment at Container Terminal Based on the Genetic Algorithm[J].Applied Mechanics and Materials，2014（5）.