基于大间隔编码的空间非负矩阵分解

Foundation items: Supported by the National Natural Science Foundation of China(61073112,61373060),the Natural Science Foundation of Jiangsu Province,China(BK2012793)and the Ph.D.Program Foundation of the Ministry of Education of China(20123218110033)

基于大间隔编码的空间非负矩阵分解*

刘大琨谭晓阳

(南京航空航天大学 计算机科学与技术学院, 江苏 南京 210016)

摘要：虽然基于局部的表示方法在图像处理中具有很好的鲁棒性,但非负矩阵分解只有隐式局部约束,导致分解不唯一和基图像不够局部.另外,局部性与判别性作为样本表示的重要性质几乎没有在非负矩阵分解中被同时考虑过.为此,文中提出了基于大间隔编码的空间非负矩阵分解,将图像数据看作像素构成的二维网络,借鉴网络中的知识将空间信息嵌入基图像,不但施加了显式的局部约束,而且能够弥补数据向量化损失的空间信息.同时,利用大间隔约束学到的额外一维空间平衡重建误差和判别性约束对基图像的影响.在AR数据库和扩展的YaleB数据库上的人脸识别实验结果表明,相比于非负矩阵及其他几种典型的扩展方法,基于大间隔编码的空间非负矩阵分解更加鲁棒.

关键词：模式分类；非负矩阵分解；空间约束；判别的子空间表示；大间隔约束

收稿日期：2014-12-15

基金项目：* 国家自然科学基金资助项目(61073112,61373060);江苏省自然科学基金资助项目(BK2012793);教育部博士点基金资助项目(20123218110033)

作者简介：刘大琨(1984-),男,博士生,主要从事机器学习、模式识别、计算机视觉研究.E-mail： liudakun315@nuaa.edu.cn

文章编号：1000-565X(2015)05-0120-06

中图分类号：TP391

doi:10.3969/j.issn.1000-565X.2015.05.019

如何从冗余的高维数据中提取鲁棒的且富有信息的表示一直以来都是各个领域较为重视的研究方向.在机器学习领域,表示学习作为研究特征变换的方向备受关注[1].但作为机器学习的一个重要分支,计算机视觉不仅增加模型的复杂度以提高表示向量的适用性,并且关注基图像的局部性与可理解性.以人脸图像为例,基向量应当提取人脸上具有语义信息的局部区域,如眼睛、鼻子、嘴等.这就需要对表示学习的模型施加一个有效的约束.为此,Lee等[2]提出了非负矩阵分解(NMF):将数据矩阵X∈Rd×m分解为两个非负矩阵B和H的乘积,即X≈BH.虽然非负矩阵分解不是一个复杂的系统,但它具有很好的特性:学到的基图像是局部的且有理论保证[3],而且符合人的直觉和认知过程,即人对于事物的认识往往从局部开始,通过非负的加权组合得到对整体的认识,而事物的局部表示也应当是非负的.

目前,对于非负矩阵分解的研究大多集中于两个方面:①施加各种具有针对性的显式局部约束[4-6].相比于整体表示方法,基于局部的表示具有更好的鲁棒性[7],而NMF的局部约束是隐式的,因此施加各种具有针对性的显式局部约束是研究的主要方面.虽然这些方法在一定程度上提高了NMF的表示能力,但忽视了图像数据特有的结构特点,即图像数据中像素之间的邻接关系.图像中像素关系的保持不但能够减轻数据向量化造成的信息损失,而且能够将图像本身内在的空间结构信息传递给模型.因此,基于像素位置的空间约束能够产生局部化的基向量.②对表示向量施加关于样本之间关系的先验信息.样本的标号信息是最早也是被重点研究的[8-10].然而,判别性与局部性约束从来没有被同时考虑过.尽管判别性和局部性能够在一定程度上相互影响,但它们的作用完全不同.仅仅施加局部约束得到的局部基图像可能具有一定的语义性,但缺乏判别力,对解决实际问题没有帮助,而仅仅考虑判别约束的则无法将先验信息有效地融入到模型中,使得学到的基图像不会具有期望的局部结构.

为此,文中提出了一种带有空间约束的判别性NMF:基于大间隔编码的空间非负矩阵分解(MMSNMF),即将图像看作由像素点组成的二维网络,采用网络结构中的度量方法计算像素之间的关系,并将拉普拉斯嵌入[11]作为空间正则化约束基图像,同时利用大间隔约束表示向量的判别性,以平衡表示向量的判别性和重建误差在模型优化中对基图像的影响.

1空间NMF模型的建立及优化

1.1模型的建立

从矩阵分解的角度来看,NMF中数据的维度和个数在数据矩阵中的地位是等价的.换句话说,NMF可以看作是对每一维特征向量的非负重建,而不仅仅是对样本的非负重建.于是,可以利用拉普拉斯正则化[12]将特征之间的结构关系嵌入非负矩阵分解中.另一方面,传统的Fisher判别准则在判别子空间表示中具有较好的理论性和实用性,对NMF的判别性约束往往都是基于该准则.但基于Fisher判别准则的NMF的判别性和数据重建误差最小化都直接约束低维表示向量.在模型优化中,表示向量的判别性导致局部的基图像,最小化重建误差产生整体的基图像[13],因此很难平衡两者之间的关系.相比之下,大间隔[14]通过函数间隔施加判别性约束,其中学到的投影向量张成额外的判别子空间,故它比非负矩阵分解的子空间维度多一维用于约束判别性,这样可以有效地减少对低维表示向量的直接约束,平衡判别性与重建在模型优化中对基图像的影响.基于大间隔编码的空间NMF模型如下:

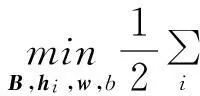
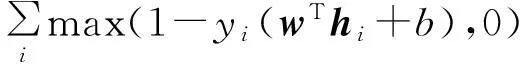
(1)

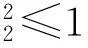
这是一个二分类模型,其中,xi是数据向量,trace(BTLB)是对基矩阵B的空间正则化,L是空间结构约束矩阵,hi是xi的子空间表示,α是正则化参数,k是子空间维度,w是权重向量,yi是样本标号,b是偏差,max(1-yi(wThi+b),0)是铰链损失,用于最大化表示向量的函数间隔.

空间结构约束矩阵L是反映像素相互关系的拉普拉斯矩阵[11],用于保留二维数据的空间信息:如果两个像素在图像上是相邻的,那么在基图像上对应位置的元素或者同时位于局部区域内部,或者同时位于局部区域外部.对于图像上像素之间邻接关系的计算,由于将图像看作像素组成的二维网络,因此可以采用网络结构中的度量方式计算.其中,比较常见的网络结构是4相邻和8相邻网络,由于8相邻网络结构存在一定的模糊性(相同的两个点之间有多种不同的通路,因而有不同的距离),故文中采用4相邻网络结构及其相应的D4距离.设图像上任意两个点p、q的坐标分别是(x,y)、(s,t),则p、q之间的距离表达式为

(2)

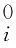
(3)

最后,通过相似度矩阵得到相应的拉普拉斯矩阵.

1.2模型的优化

为了简化优化过程,将模型(1)整理为

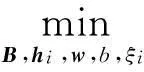
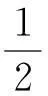
(4)

s.t.B≥0,hi≥0,ξi≥0,yi(wThi+b)≥1-ξi.

此目标函数中所有的变量可以分成3个部分:基矩阵B、关于大间隔投影的变量(w,b,ξi)、表示矩阵H(hi是H的第i列向量).文中采用交替优化求解方法,即固定任意两个而优化其他部分.

由于基矩阵和表示矩阵可以通过矩阵分解方法初始化,因此首先固定基矩阵来交替优化关于大间隔投影的变量和表示矩阵,称为内部交替优化.

在内部交替优化中,当表示矩阵H和基矩阵B被固定后,模型(4)就转化为支持向量机的形式:

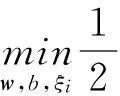
(5)

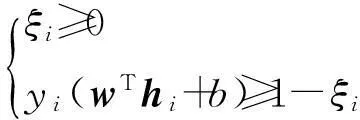
因此,可以利用各种现有工具包求解w、b、ξi.

当变量B和w、b、ξi都被固定后,模型(4)转化为一个标准的二次规划问题:

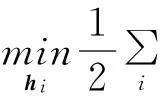
(6)

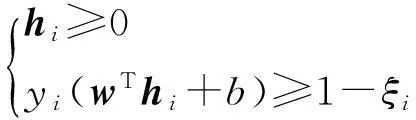
由于样本相互独立,式(6)可以进一步解耦为

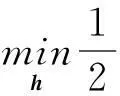
(7)

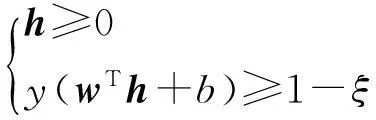
在求解B时,由于基矩阵仅与表示矩阵相关,因此在其他变量固定的情况下,模型(4)转化为带有空间约束和非负约束的矩阵分解:

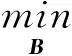
(8)

s.t.B≥0.

由于非负约束,这里采用投影梯度法来优化基矩阵.

2实验及结果分析

为了比较基矩阵的局部结构和表示矩阵的判别性对图像分类鲁棒性的影响,本实验侧重于从无噪声或低噪声的人脸图像中提取有效的模式,对光照和遮挡的人脸图像进行身份识别.这里采用的是AR和扩展YaleB人脸数据库.同时,将NMF[2]、局部约束的NMF(LNMF)[4]、带有稀疏约束的NMF(NMFsc)[5]、带有像素散度惩罚的NMF(空间NCA和空间NMF)[6]以及基于Fisher判别准则的NMF(FNMF)[8]作为对比算法.

2.1数据库介绍以及参数设定

AR数据库[15]包含70个男性和56个女性的人脸图像.每人共有26幅图像,它们是在相同的条件下等数量地采集于两个不同的时间.每个时间采集的图像包含4种表情图像、3种光照图像、2种遮挡图像及光照和遮挡共同影响的图像.实验中仅使用了100个人(50个男性和50个女性)的受单噪声影响的图像,并且所有图像对齐且向下采样到25×25.

扩展的YaleB数据库[16]包含28个人的16128幅图像.这些图像共包含9个姿态和64种光照(水平和垂直方向上不同角度的光源对人脸进行照射)效果.实验中使用仅受光照影响的图像,并且所有图像向下采样到40×45.

MMSNMF的空间正则化参数在AR人脸数据库和扩展的YalebB人脸数据库上均设为0.7,LNMF对基矩阵和表示矩阵的正则化参数在两个数据库上均分别设为0.1和0.2,NMFsc对基矩阵和表示矩阵的稀疏度约束在两个库上均分别设为0.5和0.1,空间 NMF和空间NCA的像素散度惩罚系数在两个数据库上均设为0.3,FNMF中内类和类间散度矩阵的正则化参数在两个数据库上均设为1.

2.2识别受光照影响的人脸图像

在AR或扩展的YaleB人脸数据库中,每次实验随机选择5个人的图像进行多类身份识别.由于AR人脸数据库中每人只有2幅完全无噪声的图像,因此选择受噪声影响较小的图像作为训练集.由于扩展的YaleB人脸数据库中没有完全干净的人脸图像,因此选择受光照影响相对较小的图像作为训练集,即选择光源在水平和垂直方向上与人脸中心夹角小于35°的图像作为训练集,其余光照图像作为测试集.图1展示了两个人脸数据库中的部分训练样本和光照图像测试样本示例.

图1　两个数据库中的训练样本和光照图像测试样本示例

Fig.1Examples of training samples and test samples of illumination images in two databases

在对比算法中选择支持向量机作为分类器,并采用一对多的方式训练分类器.测试样本的标号根据每个分类器的打分确定.具体地,每次选其中一个人的训练集作为正类,其余人的训练集作为负类,训练5个分类器(由于正、负类样本数不平衡,设置支持向量机中平衡正、负类的正则化参数C为100).于是,每个分类器会对测试样本给出属于每个标号的置信度,以置信度最高的身份标记测试样本.由于FNMF中没有考虑多类的情况,因此对任意两个人的训练图像分别学习分类器,并以与某个人相关的所有分类器给出的置信度均值作为测试样本相对于该类的置信度.每次实验重复10次,并以平均精度来统计各方法的性能.不同子空间维度下各种方法在两个人脸数据库上的识别性能如图2所示.从图中可知,带有判别性的方法的识别性能要优于仅带有空间约束的方法,而融合了判别性与空间约束的MMSNMF则具有更好的识别性能:NMSNMF的最高识别性能在AR和扩展的YaleB数据库上分别比FNMF高4.67%和3.11%.

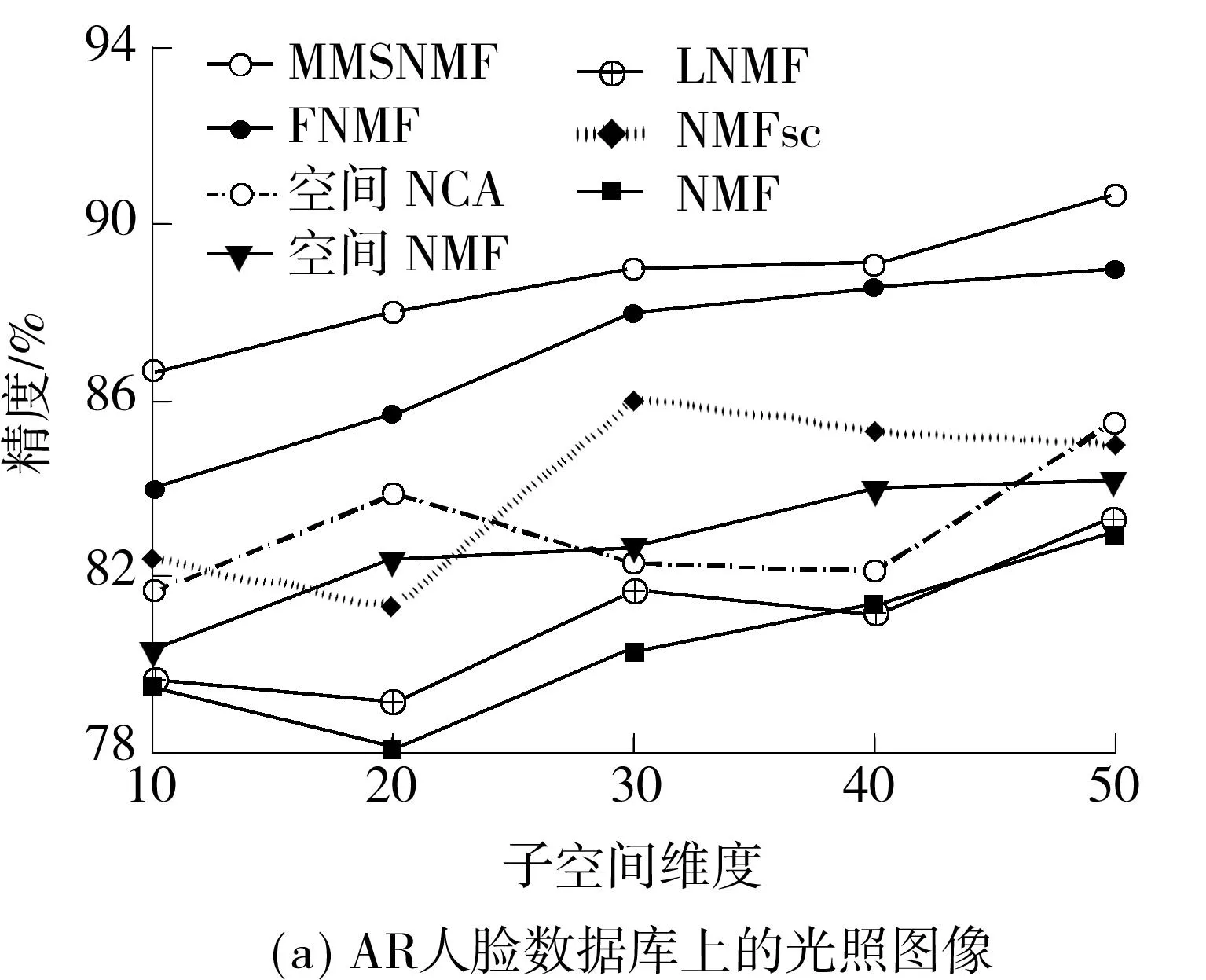
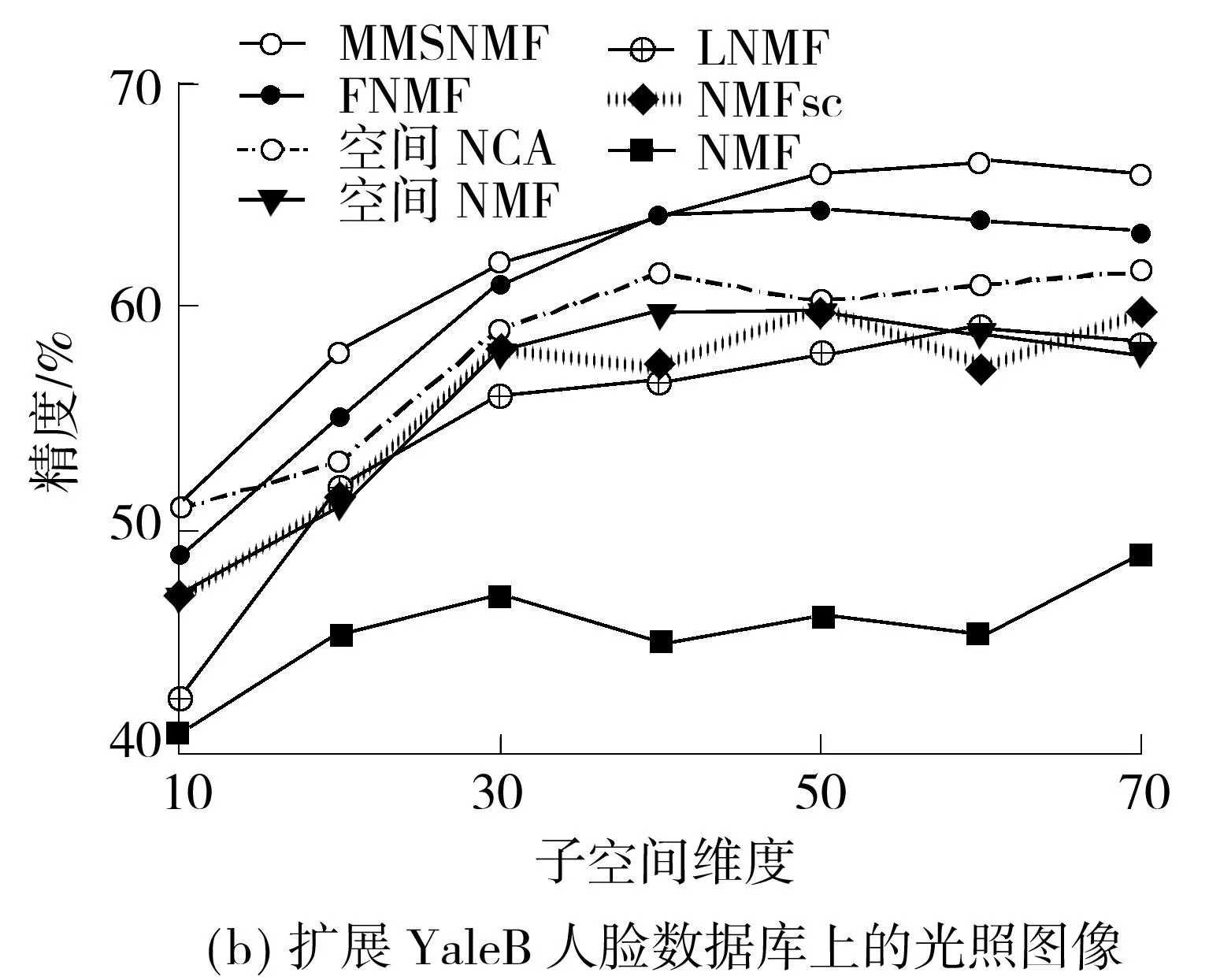
图2不同子空间维度下几种方法对光照图像的平均识别精度

Fig.2Average identification accuracies of several methods for illuminating images with different subspace dimensions

2.3识别受遮挡影响的人脸图像

由于不是专门解决遮挡问题,因此仅考虑几种比较简单的遮挡情况.在AR人脸数据库中,遮挡主要是墨镜和围巾(见图3(a)).扩展的YaleB人脸数据库中没有部分遮挡图像,故人为加入遮挡进行实验,即随机地遮挡训练图像中的一个区域,遮挡部分占图像面积的10%,如图3(b)所示.

图3　实验使用的部分遮挡图像示例

Fig.3Examples of partial occlusion images used in the experiments

整个实验过程与2.2节相同.不同子空间维度下几种方法识别部分遮挡图像的平均性能如图4所示.相比于光照实验,部分遮挡实验因遮挡面积较小,特别是扩展的YaleB人脸图像,噪声对图像的影响相对较小,因此几种方法在适当子空间维度下都能获得比较理想的性能,但从两个人脸数据库来看,MMSNMF的最高识别精度在AR和扩展的YaleB人脸数据库上分别比FNMF高3.00%和1.34%.

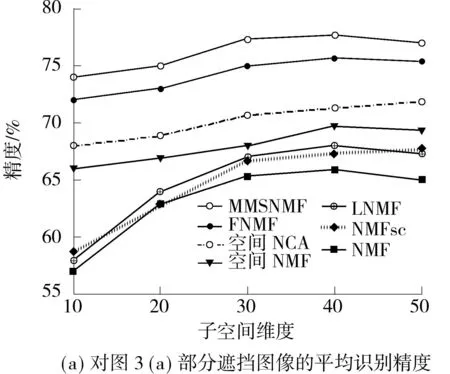
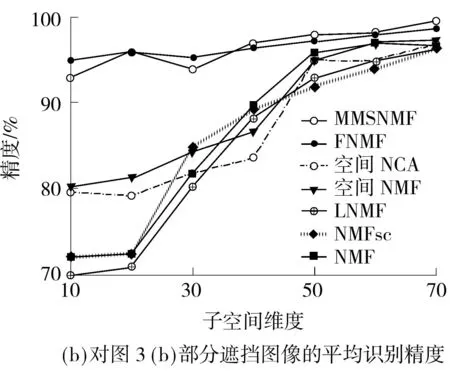
图4不同子空间维度下几种方法对部分遮挡图像的平均识别精度

Fig.4Average accuracies of several methods for identificating partial occlusion images with different subspace dimensions

各种方法在两个人脸数据库上的基图像如图5所示.其中,AR和扩展YaleB人脸数据库上子空间维度分别为10、30.为显示清晰,对所有的基图像进行了规整化.两种算法的测试精度与参数α的关系如图6所示,其中α=0时模型变为大间隔的NMF.由此可见,相比于仅仅施加大间隔约束,兼具判别性和空间性的MMSNMF具有更好的性能.

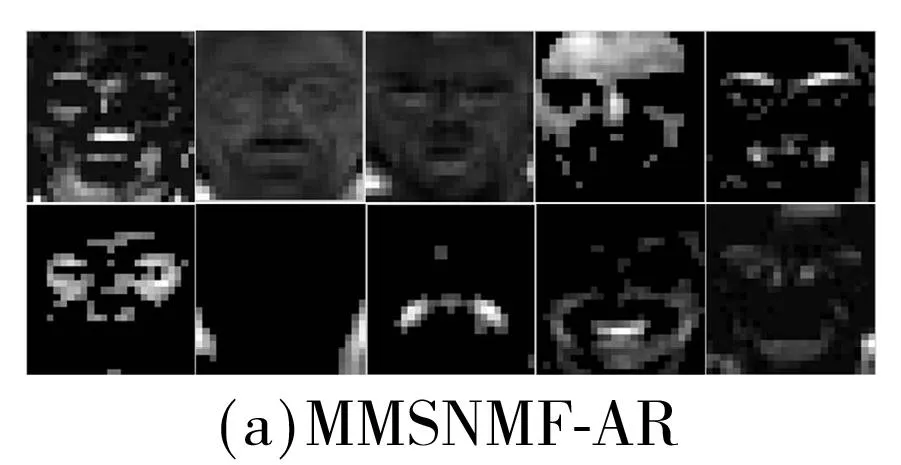
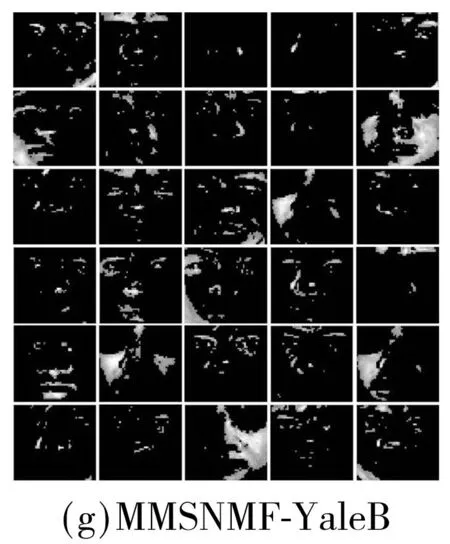
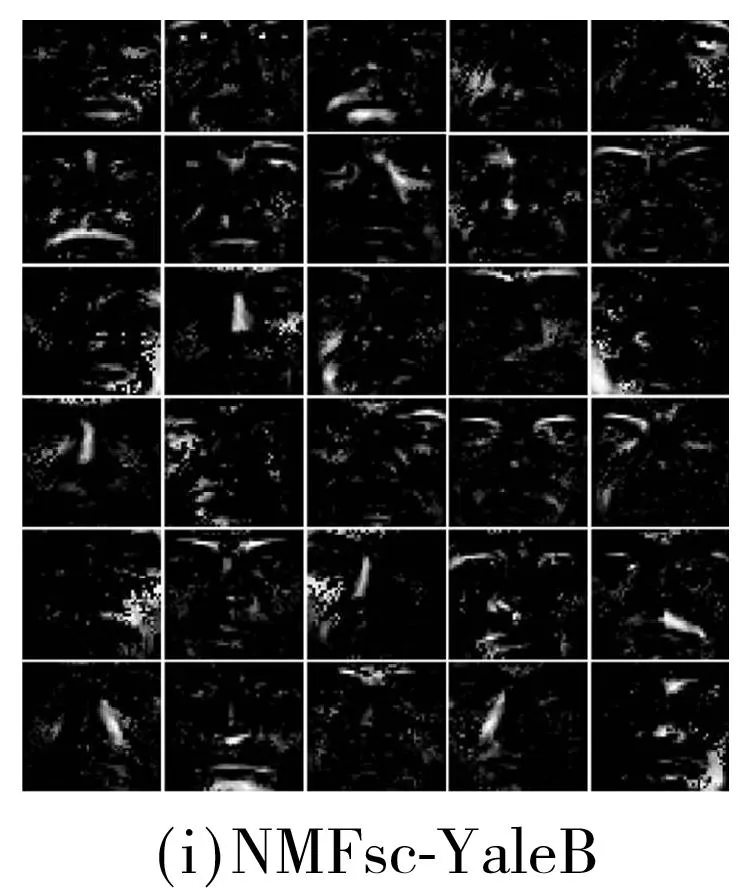
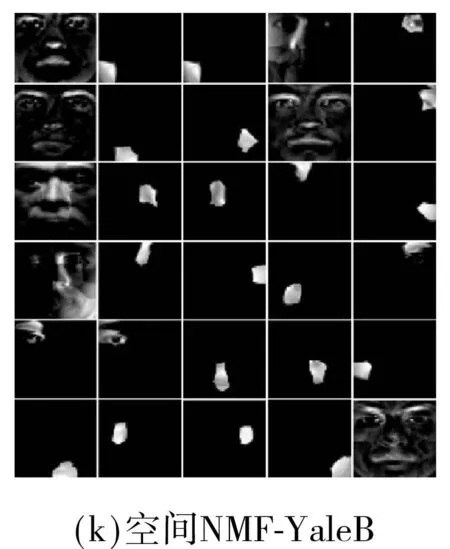
Fig.5Basis images of several methods on two face databases

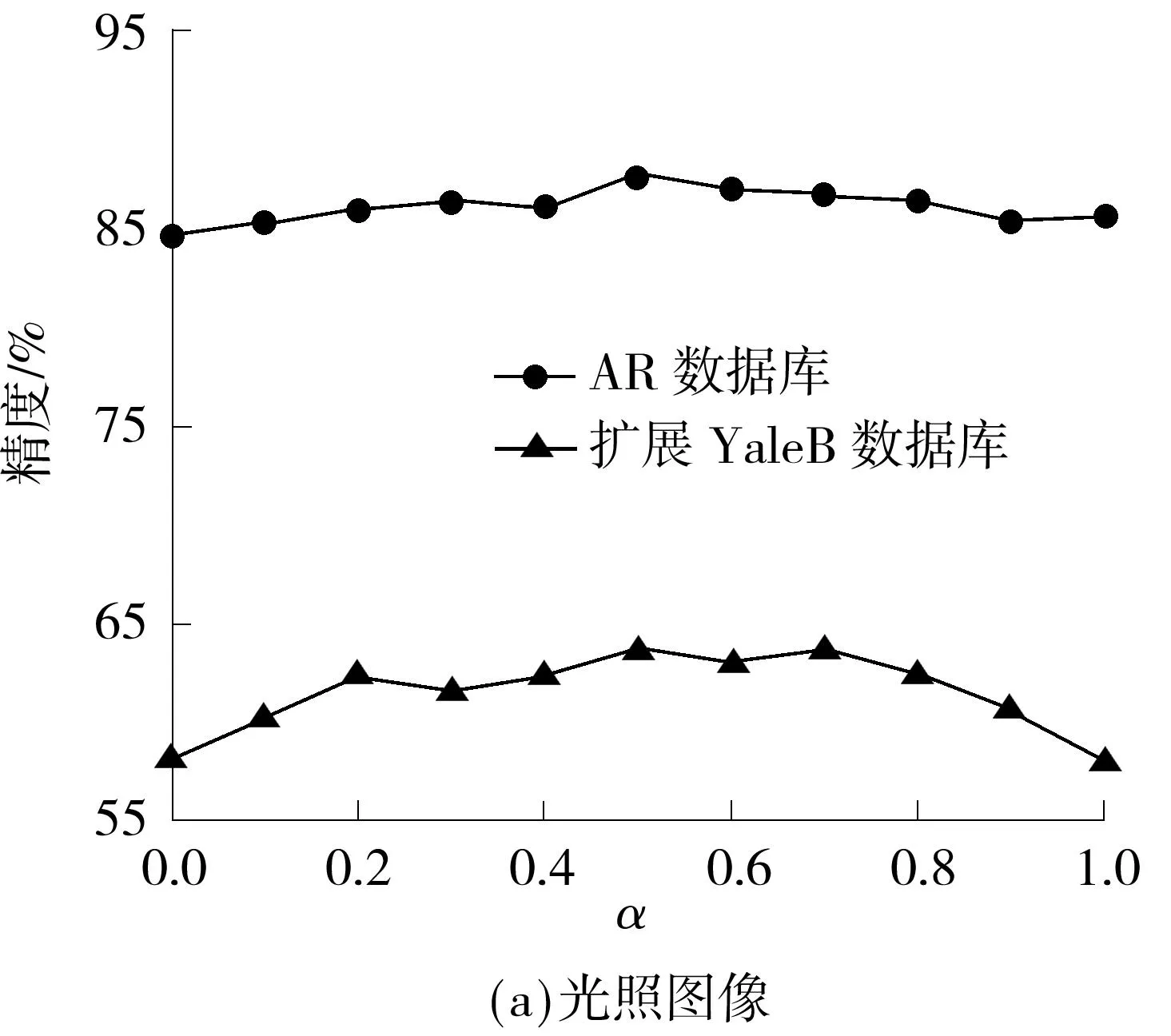
图6不同α取值下MMSNMF对光照图像和部分遮挡图像的测试精度

Fig.6Test accuracies of MMSNMF for illumination images and partial occlusion images with different values ofα

3结论

基于大间隔编码的空间NMF是一种有监督的空间NMF,它通过4相邻网络结构中的度量方式计算像素之间的邻接关系,并借鉴拉普拉斯嵌入将图像中像素之间的空间信息嵌入到NMF的基图像中.另一方面,为了缓和重建误差和判别性约束在模型优化中对基图像的矛盾,文中模型采用了大间隔编码施加判别性约束.实验结果表明,局部性与判别性约束对于NMF都是不可或缺的.

参考文献：

[1] Bengio Y,Courville A,Vincent P.Representation lear-ning:a review and new perspectives [J].IEEE Transactions on Pattern Analysis and Machine Intelligence,2013,35(8):1798-1828.

[2]Lee D D,Seung H S.Learning the parts of objects by non-negative matrix factorization [J].Nature,1999,401(6755):788-791.

[3]Donoho D,Stodden V.When does non-negative matrix factorization give a correct decomposition into parts [M].Advances in Neural Information Processing Systems 16.Cambridge:MIT Press,2003:1141-1148.

[4]Li S Z,Hou X W,Zhang H J,et al.Learning spatially localized,parts-based representation [C]∥Proceedings of the 2001 IEEE Computer Society Conference on Computer Vision and Pattern Recognition.Colorado Springs:IEEE,2001:I-207-I-212.

[5]Hoyer P O.Non-negative matrix factorization with sparseness constraints [J].Journal of Machine Learning Research,2004,5:1457-1469.

[6]Zheng W S,Lai J H,Liao S,et al.Extracting non-negative basis images using pixel dispersion penalty [J].Pattern Recognition,2012,45(8):2912-2926.

[7]张颖,余英林.鲁棒性增强的ART1神经网络 [J].华南理工大学学报:自然科学版,1994,22(5):72-79.

Zhang Ying,Yu Ying-lin.Improvement of ART1 neural architecture in robustness [J].Jouranl of South China University of Technology:Natural Science Edition,1994,22(5):72-29.

[8]Wang Yuan,Jia Yunde.Fisher non-negative matrix facto-rization for learning local features [C]∥Proceedings of Asian Conference on Computer Vision.Jeju island:Sprin-ger,2004:27-30.

[9]Zafeiriou S,Tefas A,Buciu I,et al.Exploiting discriminant information in nonnegative matrix factorization with application to frontal face verification [J].IEEE Transactions on Neural Networks,2006,17(3):683-695.

[10]Kumar B,Kotsia I,Patras I.Max-margin non-negative matrix factorization [J].Image and Vision Computing,2012,30(4):279-291.

[11]Belkin M,Niyogi P.Laplacian eigenmaps and spectral techniques for embedding and clustering [M].Advances in Neural Information Processing Systems 14.Cambri-dge:MIT Press,2001:585-591.

[12]Ando R K,Zhang T.Learning on graph with Laplacian regularization [M].Advances in Neural Information Processing Systems 19.Cambridge:MIT Press,2006:19-25.

[13]Fidler S,Skocaj D,Leonardis A.Combining reconstructive and discriminative subspace methods for robust classification and regression by subsampling [J].IEEE Transactions on Pattern Analysis and Machine Intelligence,2006,28(3):337-350.

[14]Lian X C,Li Z,Lu B L,et al.Max-margin dictionary learning for multiclass image categorization [C]∥Proceedings of the 11th European Conference on Computer Vision.Hersonissos:Springer,2010:157-170.

[15]Martínez A M,Kak A C.PCA versus LDA [J].IEEE Transactions on Pattern Analysis and Machine Intelligence,2001,23(2):228-233.

[16]Georghiades A S,Belhumeur P N,Kriegman D.From few to many:illumination cone models for face recognition under variable lighting and pose [J].IEEE Transactions on Pattern Analysis and Machine Intelligence,2001,23(6):643-660.

Spatial Non-Negative Matrix Factorization Based on Max-Margin Coding

LiuDa-kunTanXiao-yang

(College of Computer Science and Technology,Nanjing University of Aeronautics and Astronautics,Nanjing 210016,Jiangsu,China)

Abstract:Although the parts-based representation results in strong robustness in image processing, the local constraint in non-negative matrix factorization(NMF) is implicit, which leads to insufficient uniqueness and locality. Meanwhile, as two important property indexes, locality and discriminant in feature extraction are seldom considered in NMF simultaneously. In order to solve this problem, a discriminative NMF on the basis of max-margin coding is proposed. In this method, image data are regarded as a 2D network of pixels, and, on the basis of network knowledge, spatial information is embedded into basis images, which not only imposes an explicit local constraint but also compensates the spatial information loss caused by data vectorization. Additionally, an extra 1D space learned from max-margin constraint is adopted to balance the effects of reconstruction error and discriminative constraint on basis images. Experimental results on AR and extended YaleB databases for face recognition show that, in comparison with NMF and some of its variants, the proposed max-margin coding-based spatial NMF is more robust.

Key words: pattern classification;non-negative matrix factorization;spatial constraint;discriminative subspace representation;max-margin constraint