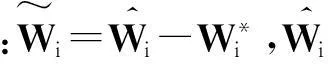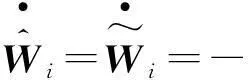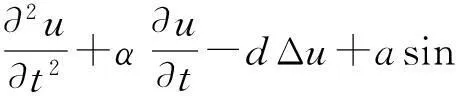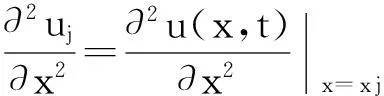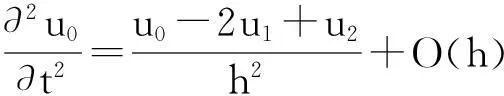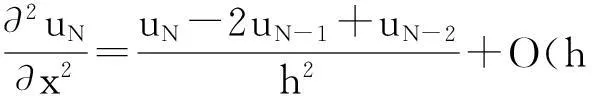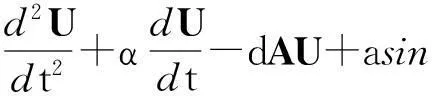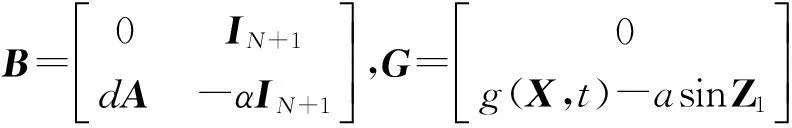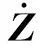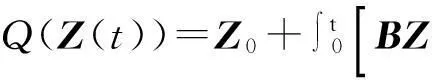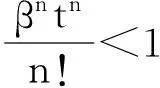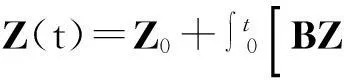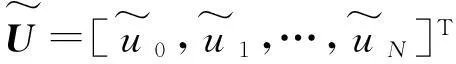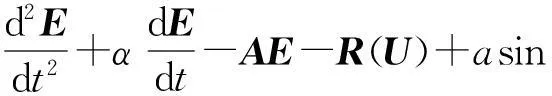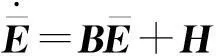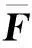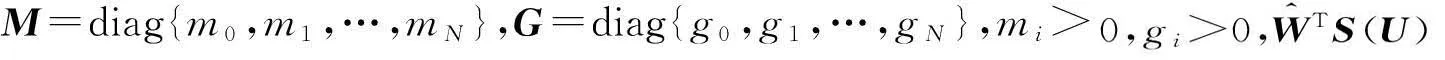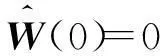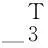基于确定学习的有阻尼受迫Sine-Gordon方程的辨识

Foundation item: Supported by the National Science Fundation for Distinguished Young Scholars of China(61225014)

† 通信作者： 王聪(1968-),男,博士,教授,主要从事智能控制、动态模式识别研究.E-mail: wangcong@scut.edu.cn

基于确定学习的有阻尼受迫Sine-Gordon方程的辨识*

董训德1,2王聪1†

(1.华南理工大学 自动化科学与工程学院, 广东 广州 510640; 2.华南理工大学 数学学院，广东 广州 510640)

摘要：文中就一类有阻尼受迫Sine-Gordon方程的系统动态进行辨识研究.首先利用有限差分理论,将由偏微分方程描述的无穷维Sine-Gordon方程近似为由一组常微分方程描述的有限维系统,然后证明该近似系统解的存在唯一性和收敛性,最后利用确定学习对该近似系统的系统动态进行辨识.实验结果表明,文中方法可实现该类Sine-Gordon方程系统动态的局部准确辨识.

关键词：Sine-Gordon方程；系统辨识；确定学习；动力学

基金项目：* 国家杰出青年科学基金资助项目(61225014)

作者简介：董训德(1985-),男,博士生,主要从事系统辨识及确定学习研究.E-mail: dong.xd@mail.scut.edu.cn

文章编号：1000-565X(2015)05-0073-05

中图分类号：TP11;N945.14

doi:10.3969/j.issn.1000-565.2015.05.012

收稿日期：2014-09-19

在众多的偏微分方程中,Sine-Gordon(SG)方程是包含时间变量的许多重要的数学物理方程之一,是一个无穷维的分布参数系统,经常出现在场论和微分几何中,并且几乎在所有的物理分支和科学理论领域都有着广泛的应用.从20世纪三四十年代开始,SG方程得到了较大的应用和发展,特别是在固体物理、低温物理、电磁学及力学领域.Josephson[1]首次将SG型本构关系用于超导体中的Josephson结,其方程形式为

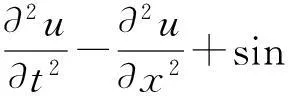
(1)

其中u=u(x,t).

作为一个有着广泛应用的数学物理方程,SG方程的动力学研究[2-4]、参数辨识[5-6]、解析解[7-9]和数值解[10-11]的求取等都受到了很多学者的关注.其中,在动力学方面主要研究系统吸引子的存在性、维数估计等问题,对SG方程的辨识研究主要针对系统参数进行辨识,而对更全面、更本质地表达系统动态行为的系统内部动态辨识却鲜有研究.实际上,分布参数系统具有无穷维性质,对其辩识是一个极具挑战性的课题.到目前为止,在此方向上的研究重点主要集中在参数辨识、系统可辨识性和辨识方法3个方面[12-13].分布参数系统的辨识与持续激励(PE)条件的满足紧密相关[12-14],持续激励条件是系统辨识领域中的一个核心概念[15-16],在分布参数系统辨识和集中参数系统辨识中都起着重要的作用.然而,对于一般的非线性系统辨识,PE条件通常难以描述并得到预先验证[17].

最近,笔者在对径向基函数(RBF)神经网络的持续激励特性研究的基础[12]上提出了确定学习理论[18].确定学习运用自适应控制和动力学系统的概念与方法,研究了未知动态环境下的知识获取、表达、存储和利用等问题.针对产生周期或回归轨迹的连续非线性动态系统,确定学习可以对其未知系统的动态进行局部准确辨识.

利用确定学习理论,文中对如下有阻尼受迫SG方程:

(2)

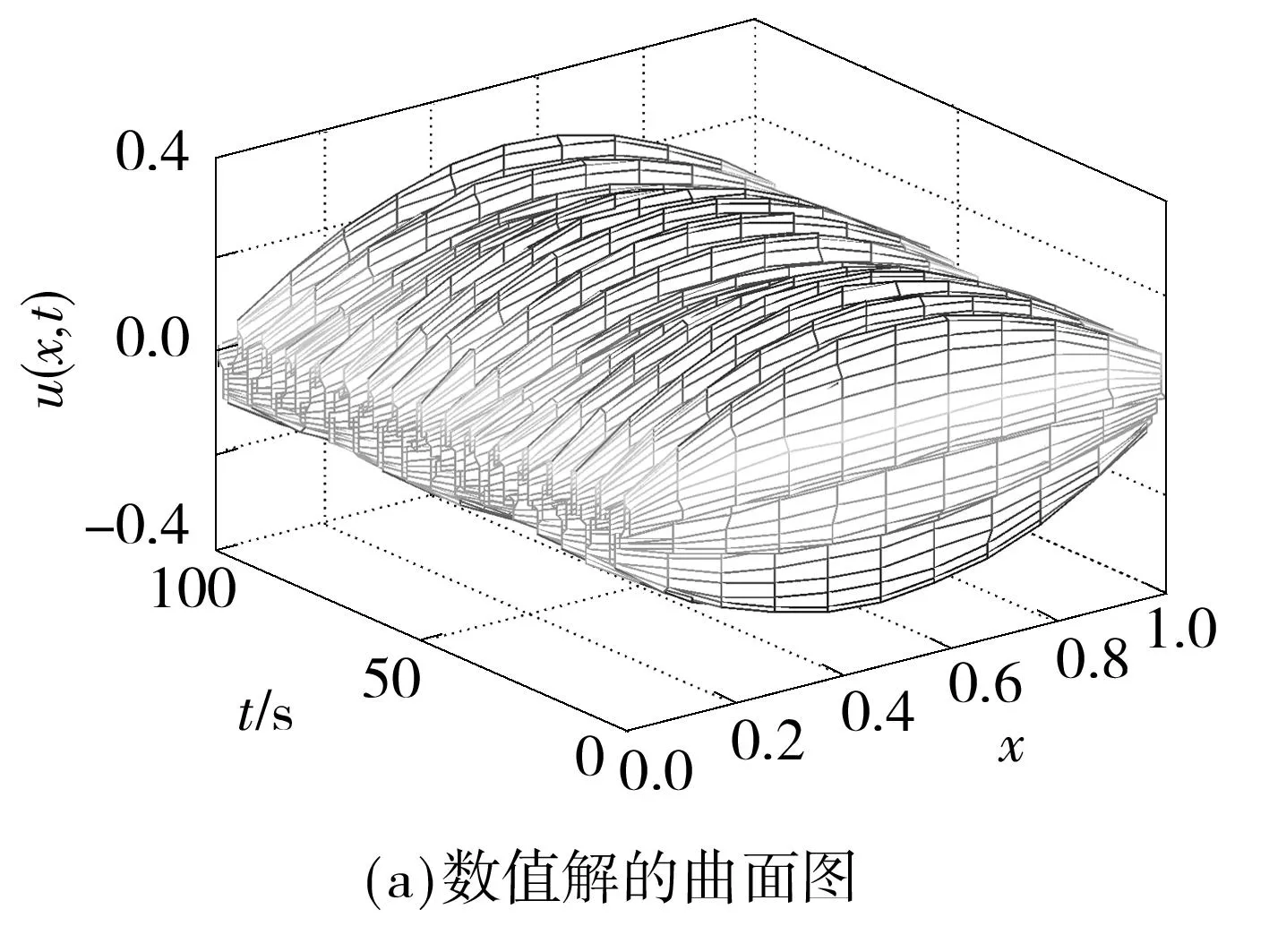
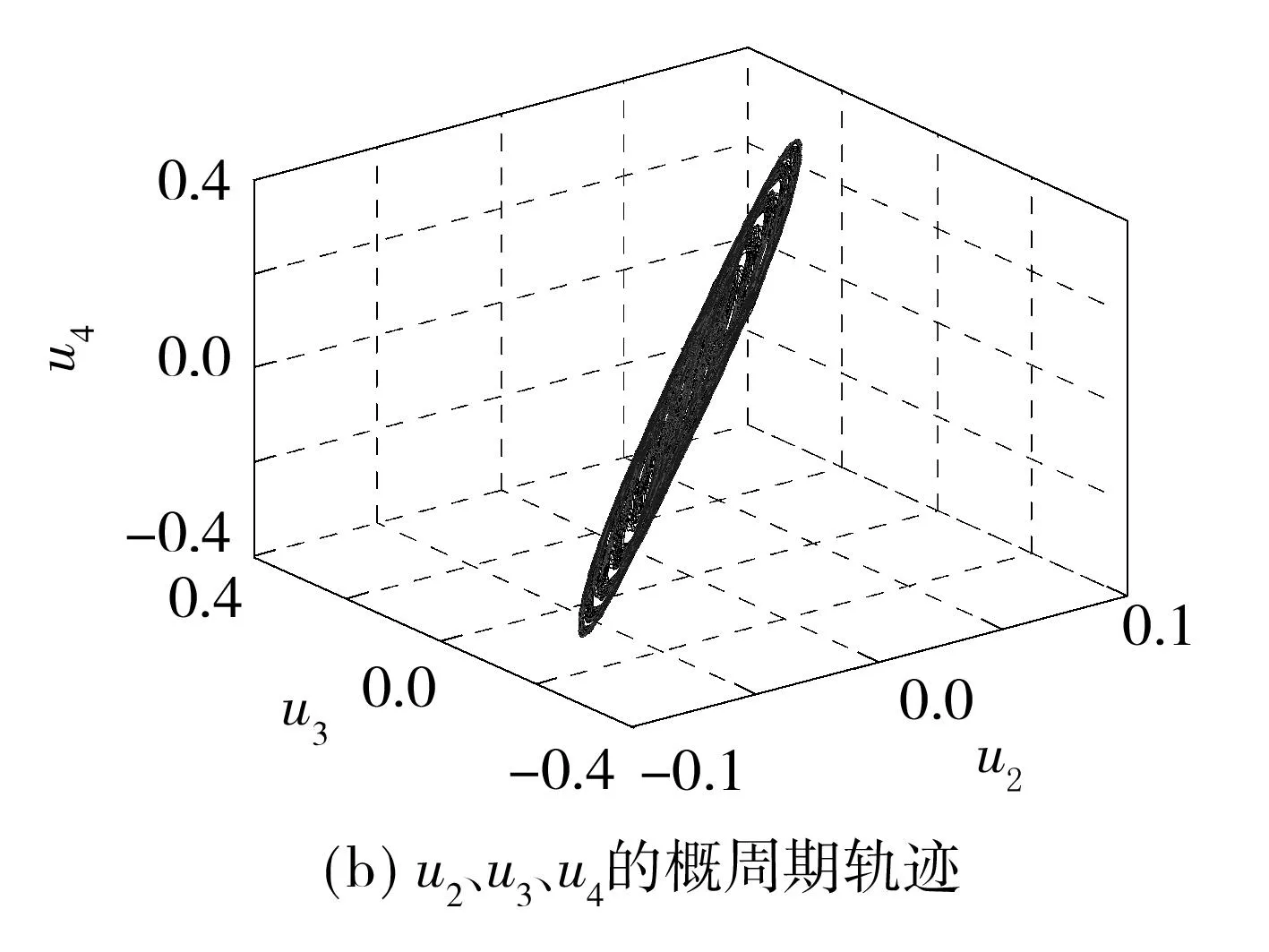
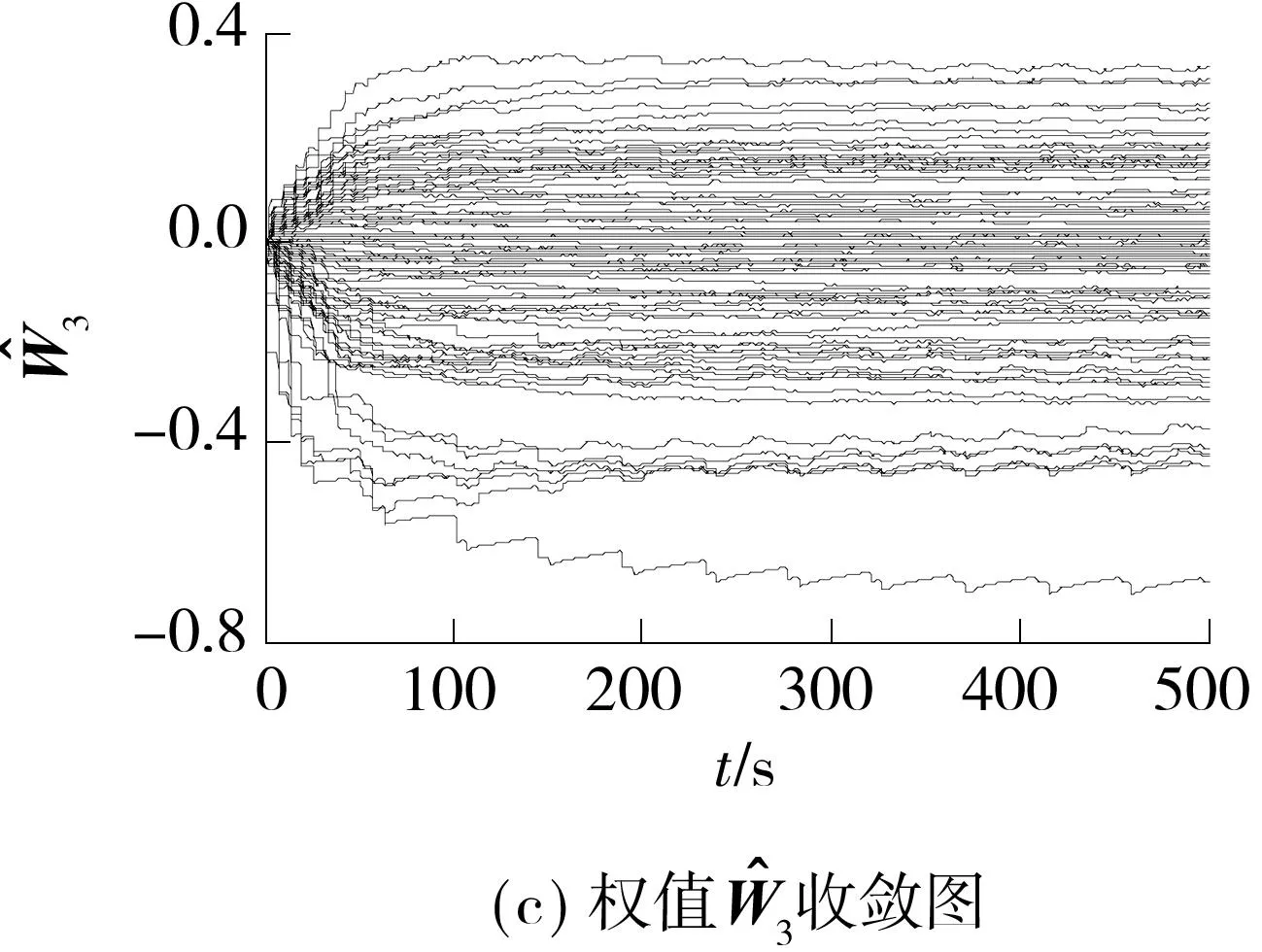
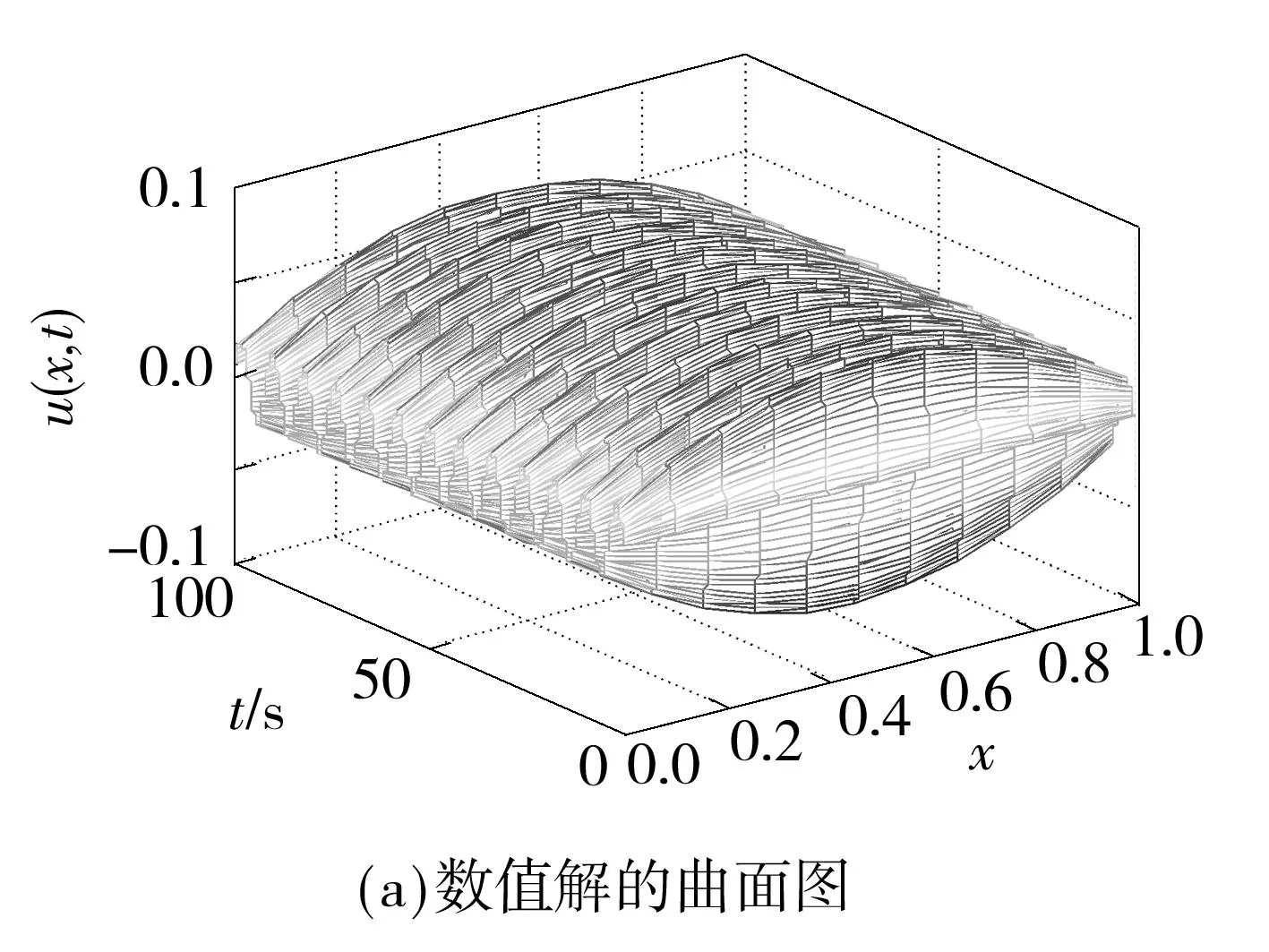
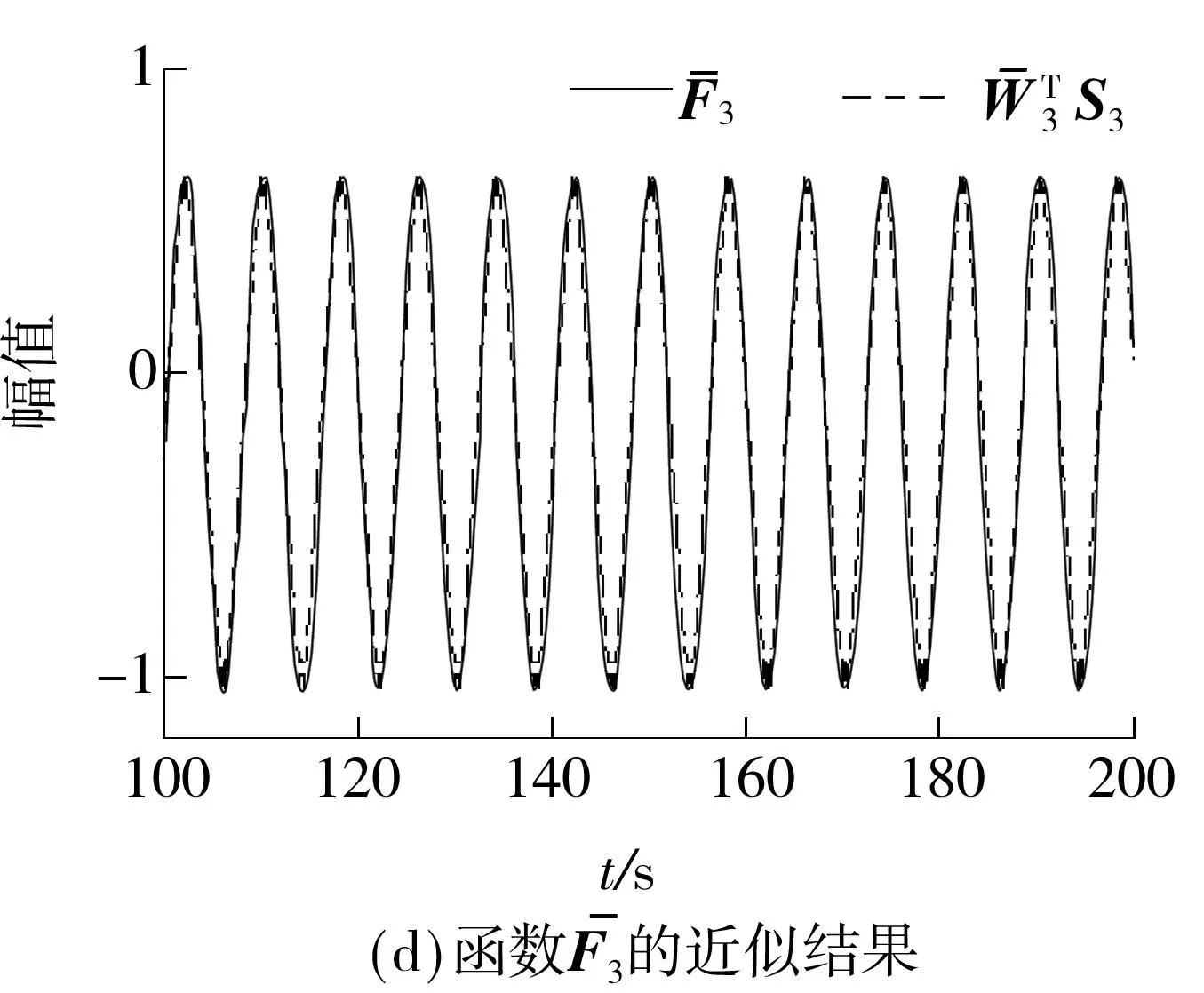
(1)若d=1,g(x,t)是t的概周期函数,且0

(2)若g(x,t)=I(x)+f(x)sin(ωt),且a=1,则可得到方程

1确定学习理论

考虑如下的非线性动态系统:

(3)

式中:x=[x1,x2,…,xn]T∈Rn,是可测的系统状态;p是系统的常值参数向量,不同的p产生不同的动态行为;F(x;p)=[f1(x;p),f2(x;p),…,fn(x;p)]T,是未知的光滑非线性向量场.假定系统状态x保持一致有界,即x(t)∈Θ⊂Rn,∀t≥t0,其中Θ是一个紧集,且以x0为起点的系统轨迹φζ(x0)是回归轨迹.

考虑如下的动态径向基函数(RBF)神经网络模型:

(4)

(5)

(6)

2Sine-Gordon方程的有限维近似

文中采用有限差分法的一种特殊形式——直线法[21]来实现SG方程的有限维逼近,针对SG方程,将空间偏导数用有限差分来代替.为叙述方便,考虑如下的一维有阻尼受迫SG方程:

(7)

(8)

其中,h是空间等分间隔.

注1由于j=0和j=N时,式(8)会产生两个虚拟点-1和N+1,因此当j=0和j=N时分别使用如下公式:

在此基础上,记U=[u0,u1,…,uN]T,系统(7)可离散为如下形式:

(9)

(10)

(11)

2.1解的存在性和唯一性分析

对任意给定的初始条件Z(0)=Z0,首先在距离空间C[0,T]中构造一个到其自身的映射Q:

其距离定义为

ρ(x,y)=‖x-y‖∞，x,y∈C[0,T].

为简化起见,下文中把下标∞省略.显然Z∈C[0,T],任取S∈C[0,T],有

(12)

对式(12)两边求微分易知,Z(t)为系统(11)的解.这就证明了系统(11)解的存在性和唯一性.

2.2解的收敛性

(13)

做适当变换可以得到如式(11)的形式:

由拉格朗日中值定理可知:

另外,

(14)

又由于

因此可以得到:

由Gronwall不等式可知:

这就证明了系统(11)的解收敛到系统(10)的解.

3SG方程近似系统的动态辨识

为方便分析,将系统(10)改写为

(15)

(16)

(17)

设计如下基于Lyapunov的权值学习律:

(18)

其中,Γ=ΓT>0,σ>0是一个很小的设计参数.

考虑由式(16)-(18)组成的自适应系统,由确定学习理论[18,22]可知,对任意始于U0=U(0)的周

4仿真结果

5结论

文中对满足一定条件下的有阻尼受迫SG方程的系统动态进行了辨识,由于SG方程是一个无穷维的分布参数系统,文中采用有限差分方法对其进行降维处理,将其近似为一组常微分方程组,并对近似系统解的存在唯一性和收敛性进行了研究,最后证明了其系统动态可利用确定学习理论实现准确辨识.仿真结果表明,具有回归轨迹的有阻尼受迫SG方程的系统动态确实得到了准确辨识.

图1　系统(2)在条件(I)下的仿真结果

图2　系统(2)在条件(II)下的仿真结果

参考文献：

[1]Josephson B D.Possible new effects in super conductive tunneling [J].Physics Letters,1962,1(7):251-253.

[2]Johnson S,Biswas A.Breather dynamics of the Sine-Gordon equation [J].Communications in Theoretical Phy-sics,2013,59(6):664-670.

[3]Gulevich D R,Gaifullin M B,Kusmartsev F V.Controlled dynamics of sine-Gordon breather in long Josephson junctions[J].The European Physical Journal B:Condensed Matter and Complex Systems,2012,85(1):1-5.

[4]Li Fei,Pan Chang-ning,Zhang Dong-xia,et al.Chaotic dynamics of a Josephson junction with nonlinear damping [J].Chinese Physics Letters,2010,27(5):050501-050503.

[5]Gutman S,Ha J H.Identification problem for damped Sine-

Gordon equation with point sources [J].Journal of Mathematical Analysis and Applications,2011,375(2):648-666.

[6]Ha J H,Nakagiri S.Identification of constant parameters in perturbed Sine-Gordon equations [J].Journal of the Korean Mathematical Society,2006,43(5):931-950.

[7]Roblesr-Pérez A M.Almost periodic solutions of forced Sine-Gordon equation [C]∥Proceedings of 2003 International Conference on Differential Equations.Singapore:World Scientific Publishing Co Pte Ltd,2005:258-263.

[8]Sun Y.New travelling wave solutions for Sine-Gordon equation [J].Journal of Applied Mathematics,2014,2014:841416.

[9]Yang Z,Zhong W P.Analytical solutions to Sine-Gordon equation with variable coefficient [J].Romanian Reports in Physics,2014,66(2):262-273.

[10]Jiang Z W,Wang R H.Numerical solution of one-dimensional Sine-Gordon equation using high accuracy multiquadric quasi-interpolation[J].Applied Mathematics and Computation,2012,218 (15):7711-7716.

[11]套格图桑.Sine-Gordon型方程的无穷序列新精确解[J].物理学报,2011,60(7):070203.

Tao Ge-tu-shang.New infinite sequences exact solutions to Sine-Gordon-type equations [J].Acta Physica Sinica,2011,60(7):070203.

[12]Demetriou M A,Rosen I G.On the persistence of excitation in the adaptive excitation of distributed parameter systems [J].IEEE Transactions on Automatic Control,1994,39(5):1117-1123.

[13]Demetriou M A,Rosen I G.Adaptive identification of se-cond-order distributed parameter systems [J].Inverse Problems,1994,10(2):261-294.

[14]Hong K S,Bentsman J.Direct adaptive control of parabolic systems:algorithm synthesis and convergence and stability analysis [J].IEEE Transactions on Automatic Control,1994,39(10):2018-2033.

[15]Narendra K S,Annaswamy A.Stable adaptive systems [M].Englewood Cliffs:Prentice-Hall,1989.

[16]Sastry S S,Bodson M.Adaptive control:stability convergence and robustness [M].Englewood Cliffs:Prentice-Hall,1989.

[17]Gevers M.A personal view of the development of system identification:a 30-year journey through an exciting field [J].Control Systems,2006,26(6):93-105.

[18]Wang C,Hill D J.Deterministic learning theory for identification,recognition,and control [M].Boca Raton:CRC Press,2009.

[19]朱澍,周盛凡.有阻尼受迫Sine-Gordon方程的全局周期吸引子[J].数学学报,1999,42(5):809-814.

Zhu Shu,Zhou Sheng-fan.Global periodic attractor for the damped and driven Sine-Gordon equation [J].Acta Mathematic Sinica,1999,42(5):809-814.

[20]Powell M J D.The theory of radial basis function appro-ximation in 1990 [J].Advances in Numerical Analysis,1992,2:105-210.

[21]Schiesser W E.The numerical method of lines [M].San Diego:Academic Press,1991.

[22]Wang C,Hill D J.Deterministic learning and nonlinear observer design [J].Asian Journal of Control,2010,12(6):714-724.

Identification of Damped and Driven Sine-Gordon

Equation Based on Deterministic Learning

DongXun-de1,2WangCong1

(1.School of Automation Science and Technology, South China University of Technology, Guangzhou 510640, Guangdong, China;

2.School of Mathematics,South China Unirersity of Technology,Guangzhou 510640,Guangdong,China)

Abstract:Discussed in this paper is the identification of dynamics of a class of damped and driven Sine-Gordon (SG) equation.Firstly,SG equation described by partial differential equation(PDE), which is infinite dimensional,is approximated by a set of ordinary differential equation with finite dimension by means of finite difference method. Then, the existence, uniqueness and convergence of the solution of the approximated system are proofed. Finally, the dynamics of the approximated system is identified on the basis of deterministic learning. Experimental results show that the proposed method helps achieve locally accurate identification of SG equation dynamics.

Key words: Sine-Gordon equation;system identification;deterministic learning;dynamics