基于原问题求解的非稀疏多核学习方法

Foundation items: Supported by the National Natural Science Foundation of China(11301106) and the Natural Science Foundation of Guangxi Province(2014GXNSFAA1183105)

† 通信作者： 丁立新(1967-),男,教授,博士生导师,主要从事机器学习、智能计算及其理论研究.E-mail: lxding@whu.edu.cn

基于原问题求解的非稀疏多核学习方法*

胡庆辉1,2丁立新1†刘晓刚2李照奎1

(1.武汉大学 计算机学院∥软件工程国家重点实验室， 湖北 武汉 430072;

2.桂林航天工业学院 广西高校机器人与焊接技术重点实验室培育基地， 广西 桂林 541004)

摘要：传统的多核学习方法通常将原问题转换为其对偶问题再进行求解,但直接求解原问题比求解对偶问题有更好的收敛属性.为此,文中提出了一种在原问题上求解、LP范数约束的非稀疏多核学习算法,首先采用次梯度和改进的拟牛顿法求解支持向量机(SVM),然后通过简单计算求解基本核的权系数.由于拟牛顿法具有二次收敛性,并且不需要计算二阶导数来得到Hessian矩阵的逆,因此文中算法具有更快的收敛速度.仿真结果表明,文中算法不仅具有较好的分类精度和泛化性能,还具有较快的收敛速度及很好的可扩展性.

关键词：多核学习;拟牛顿法;两步优化;支持向量机

基金项目：* 国家自然科学基金资助项目(11301106);广西自然科学基金资助项目(2014GXNSFAA1183105);广西高校科研重点资助项目(ZD2014147);广西高校科研项目(YB2014431);桂林航天工业学院科研基金资助项目(Y12Z028)

作者简介：胡庆辉(1976-),男,在职博士生,桂林航天工业学院副教授,主要从事多核学习、监督学习、半监督学习及数据挖掘研究.E-mail: huqinghui2004@126.com

文章编号：1000-565X(2015)05-0078-08

中图分类号：TP181

doi:10.3969/j.issn.1000-565X.2015.05.013

核方法是一种有效解决非线性模式识别的方法,但传统的核方法绝大多数是基于单个特征空间映射的单核学习方法,它需要手动选择核函数,调整其参数,不同的核函数及参数设置往往使得模型的性能表现出很大差别,并且对于包含有异构信息[1]、在高维特征空间分布不平坦[2]以及不规则的样本数据[3],采用单核进行映射对数据的处理不一定合适.近年来,基于多个核函数组合的多核学习方法得到了广泛的研究[4-11].多核学习方法是一种灵活性更强的基于核的学习方法,相对于传统的单核学习方法,它有更强的可解释性和可扩展性,在解决实际问题,如信号处理中的语音识别[12]、生物信息中蛋白质之间相互作用的抽取[13]以及数据挖掘中异常数据的检测[14]等方面,往往能够取得更好的泛化性能.

通常,一种简单且有效的多核学习方法是考虑多个基本核函数的线性凸组合[6-7,10-17].在多核学习框架下,样本在特征空间中的表示问题转化为基本核与权系数的选择问题.近年来,人们已经提出了多种有效的多核学习方法,如基于二次约束型二次规划(QCQP)的方法[4]、半定规划(SDP)方法[15]和半无限线性规划(SILP)方法[16].以上方法的优化目标函数都包含了混合范数正则化项,导致算法的收敛速度慢,为此文献[6]中提出了一种简单多核学习方法(SimpleMKL),将混合范数正则化项转化为加权二范数正则化项,并证明了两者的等价性,从而将目标函数转化为凸优化问题.随后针对该问题的权系数,人们提出了不同的优化方法,如文献[7]的二阶牛顿优化算法(HessianMKL)和文献[9]的扩展分层优化算法(LevelMKL)等.

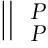
传统的多核学习方法通常是将目标函数转化为鞍点问题并通过原问题的对偶进行求解,而求解原问题与求解对偶问题是等价的.研究表明,直接求解原问题比求解对偶问题有更好的收敛属性[18].文献[19]中将目标函数转换为双凸优化问题,并利用截断牛顿法直接求解原问题,实现了稀疏的多核学习;文献[20]中采用了预处理共轭梯度法求解原问题,实现了非稀疏的多核学习.与前面的方法不同,文中提出了一种新的基于原问题求解的非稀疏多核学习方法(QN-MKL),首先采用次梯度和改进的拟牛顿法subLBFGS[21]求解支持向量机(SVM),然后通过计算求解基本核的权系数,最后通过实验验证该方法的有效性.

1多核学习的基本问题

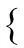
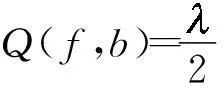
(yi,f(xi))=max(0,1-yi

决策超平面定义为

由于标量b只改变超平面的位置而不改变方向,为了便于计算,这里将b省略,即φ(x)=f(x).最后可以通过f(x)的符号判断x所属的类别:若f(x)>0,则x属于+1类;若f(x)<0,则x属于-1类.

式中,αi为膨胀系数.则式(1)转化为

其中α=(α1，α2,…,αn)T.

设φm:X→Hm(m=1，2,…,M)为给定的M个不同特征映射,Hm对应的核函数为km(·),则基于多核学习方法的目标是学习这M个核的线性凸组合,即

其中θm为基本核的权系数.在多核学习框架下,决策函数定义为

将式(6)代入式(5),得到基于原问题求解的多核学习的优化目标函数为

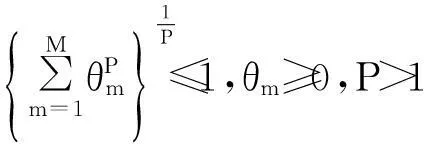
式中,Km为第m个核对应的Gram矩阵,Km(i)为Km的第i列向量.文中对权系数θ施加了P>1范数约束,以得到核函数的非稀疏组合.

2优化过程

文中采用传统的两步优化方法对Q(α,θ)进行优化[6,8-9].首先固定θ,优化关于α的非平滑函数,然后固定α,优化关于θ的带约束非线性单调函数,重复这两个过程直到满足事先设定的收敛准则.

固定θ,函数(8)是关于α的非平滑凸优化问题,文中利用次梯度和改进拟牛顿法subLBFGS[21]来求解α.

在优化α的过程中,为了使用subLBFGS算法,首先设E、R和W分别表示输入数据集中被错误分类、被分在边界区域及被正确分类的样本数据下标集合,即

subLBFGS算法在寻找下降方向p时,需要从当前迭代的任意次梯度开始,式(8)关于α的次梯度(梯度)为

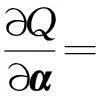
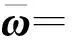
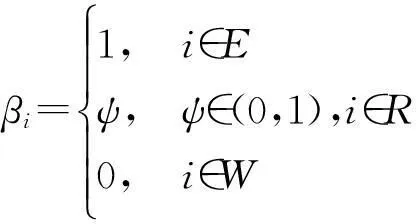
对于给定的下降方向p,需要计算该方向与次微分内积的上确界,即

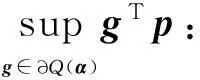
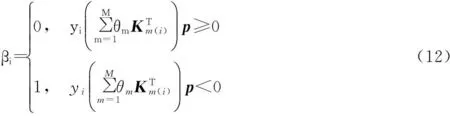
得到了确切的下降方向p后,需进行一维线性搜索确定最佳步长η,即求解如下最小化问题:

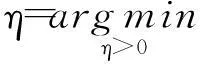
求解α的具体算法描述如下:

{ 输入:初始的α

输出:优化后的α

初始化t=0,Bt=I,αt=α;

利用式(10)计算当前任意次梯度gt;

repeat

利用subLBFGS寻找下降方向pt;

if pt=null then

break;

endif

利用式(13)执行一维线性搜索,寻找最佳步长ηt;

st=ηtpt;αt+1=αt+st;

利用式(10)计算任意次梯度gt+1∈∂Q(αt+1),使

(αt+1-αt)Tst>0;

利用BFGS公式更新矩阵Bt+1;

t=t+1;

until满足收敛条件}

求解基本核的权系数的方法如下:

由式(7)有

(14)

式中,αi(m)为第m个核对应的第i个膨胀系数,结合式(4)可得α(m)=θmα.于是式(8)转化为

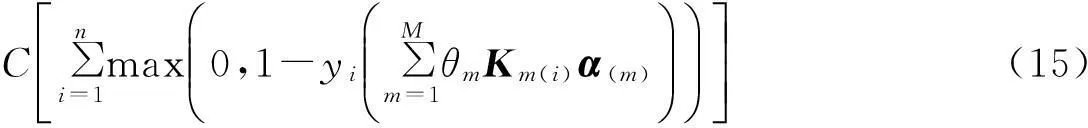
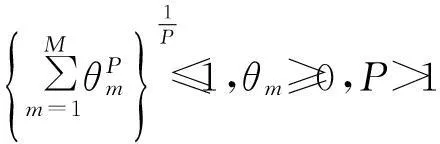
固定α(m)(m=1,2,…，M),求解θ等价于求解如下带约束的最小化优化问题:

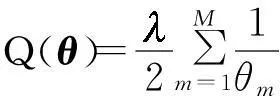
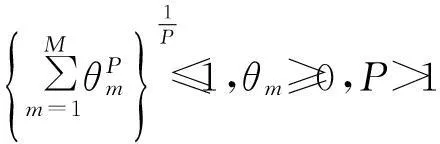
优化式(16),最后得到权系数

(m=1,2,…，M)

QN-MKL算法描述如下:

{ 输入:数据集(x1，y1)，…,(xn，yn)

输出:α,θ

repeat

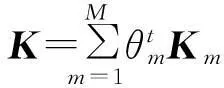
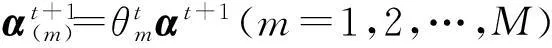
用式(17)计算θt+1;

t=t+1;

until满足收敛条件}

QN-MKL算法的循环是两步优化的过程,可以以循环次数或权系数的收敛作为结束条件.

3实验

为验证文中算法的性能,文中比较了标准SVM(采用libsvm软件包)、简单多核学习算法SimpleMKL[6]、二阶牛顿法HessianMKL[7]、基于原问题求解的算法PrimalMKL[19]、LP范数约束的非稀疏多核学习算法LP-MKL[11]和文中算法的实验结果.使用的标准数据集见表1,实验环境为Windows8 64位操作系统,Intel(R)Core(TM)i5 2.80GHz,16GB内存,仿真软件为Matlab7.10.0.499.

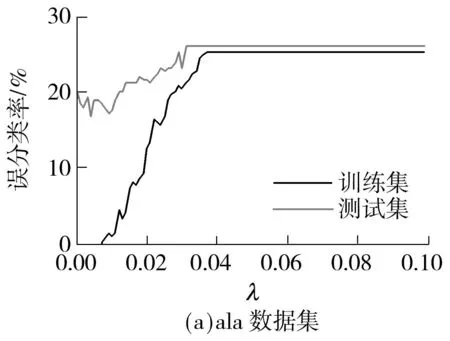
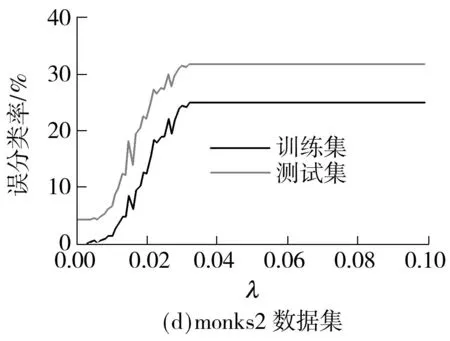
3.1参数设置

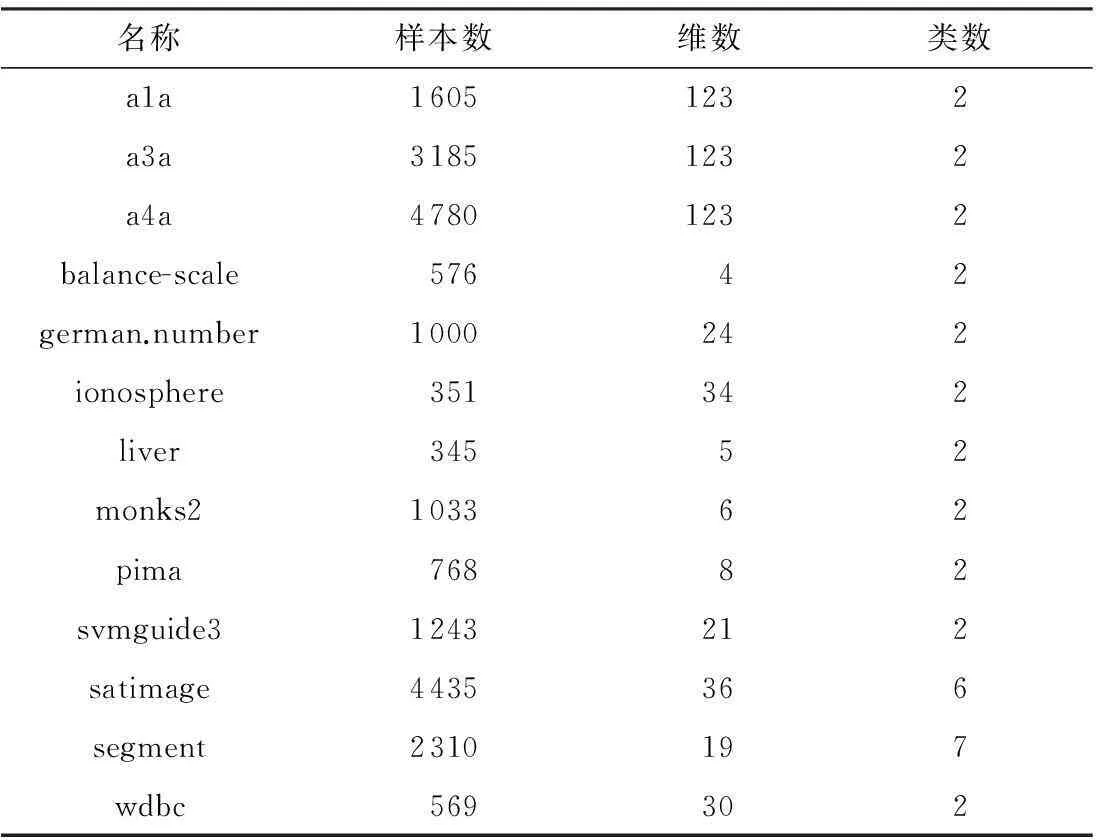
表1　数据集信息

3.2实验结果分析

(1)性能比较

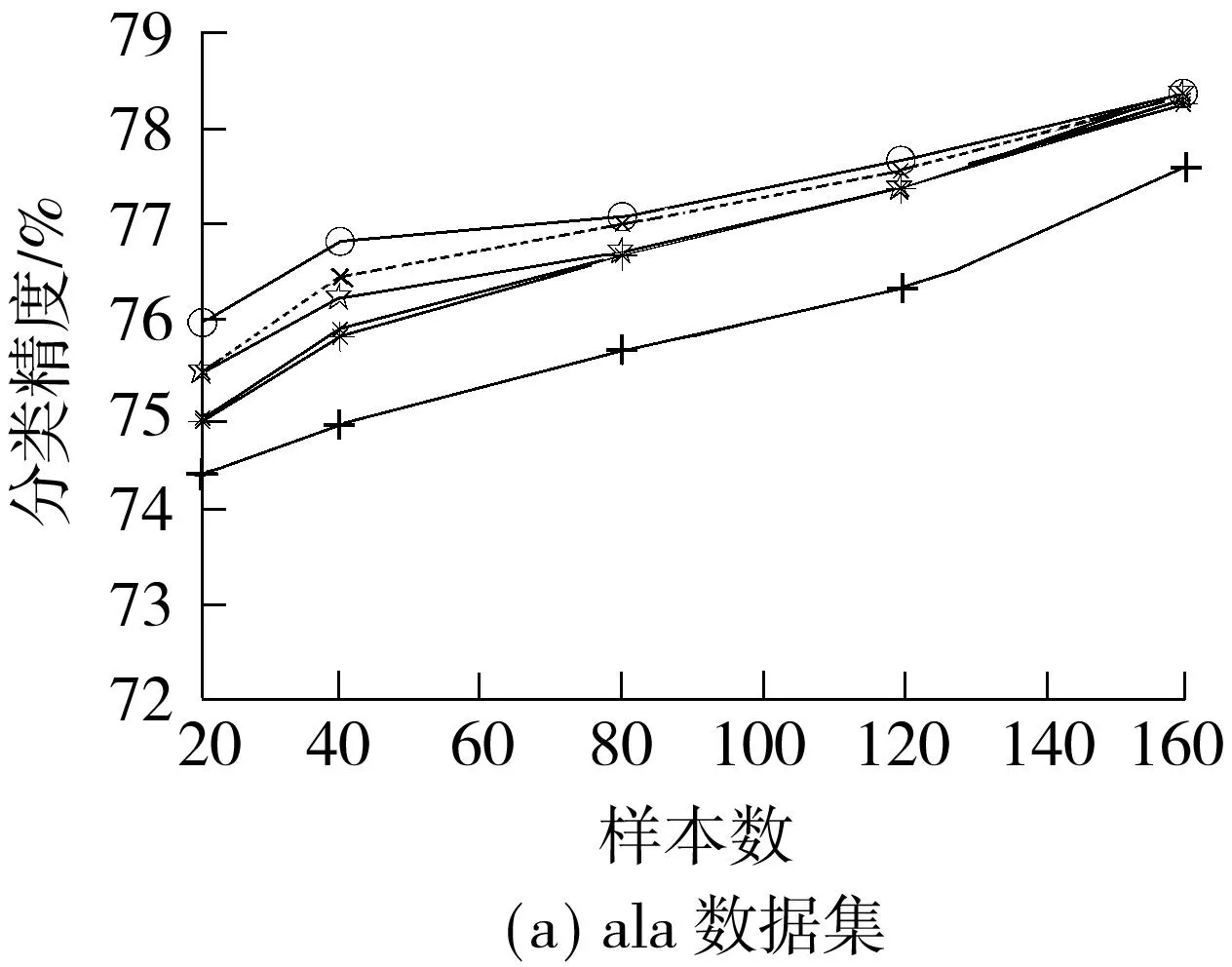
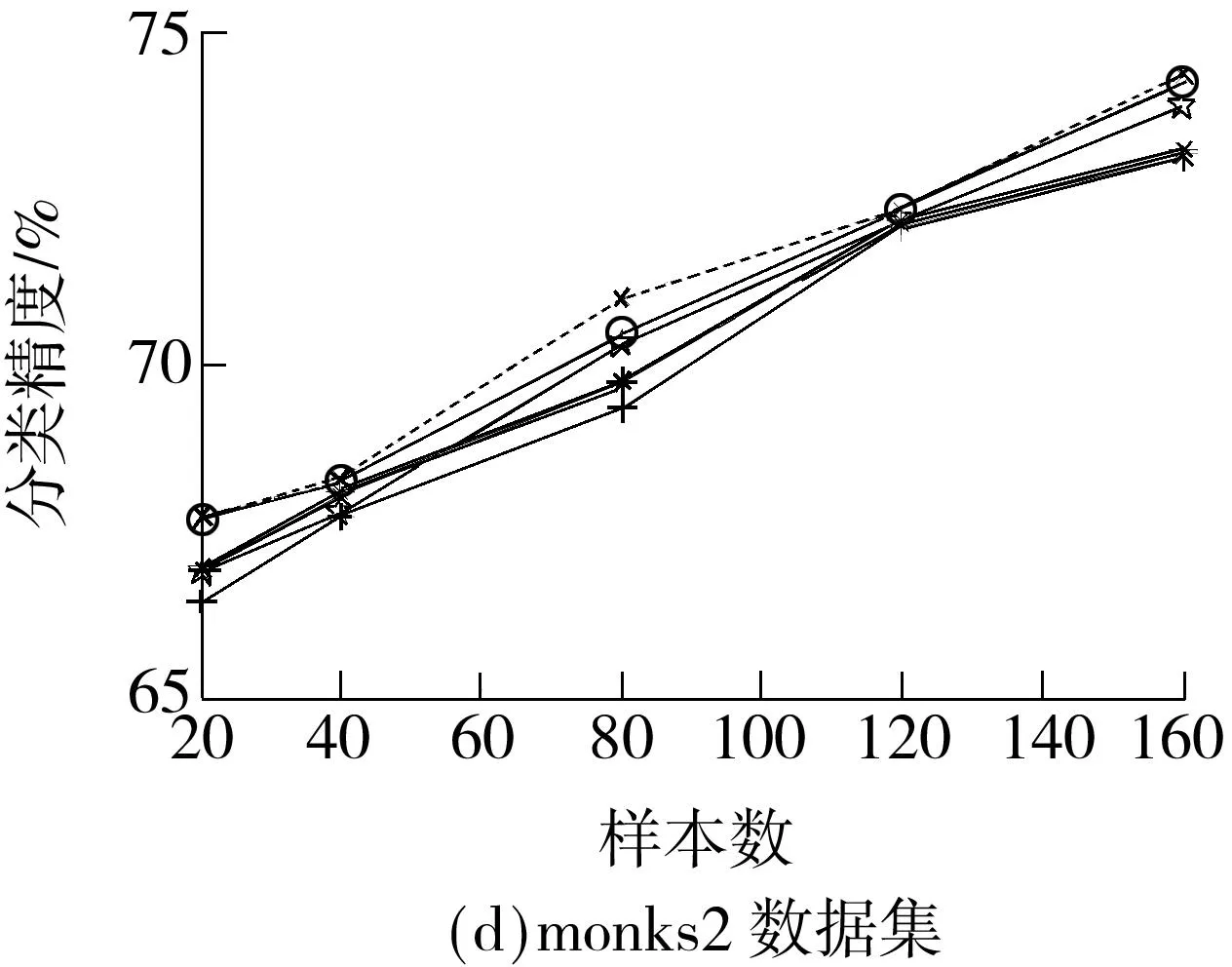
首先在6个数据集(a1a、balance-scale、ionosphere、monks2、wdbc、pima)上随机选择一定数据作为训练集,其余作为测试集,每种情况执行10次,得到几种算法的分类精度与训练样本数之间的关系如图1所示.除monks2数据集以外,QN-MKL都保持有较好的分类性能,特别是在训练样本较少的情况下,QN-MKL的分类精度高于其他算法,这表明QN-MKL具有较好的泛化性能.

随机选择13个数据集中30%的数据作为训练集,其余作为测试集,每种情况运行10次求平均,最后得到6种算法对测试集的平均分类精度和标准差,如表2所示.从表中可以看出,单核的SVM分类结果较差,非稀疏多核学习算法LP-MKL、QN-MKL的分类精度要比其他稀疏学习算法高,QN-MKL与LP-MKL的分类精度比较接近.

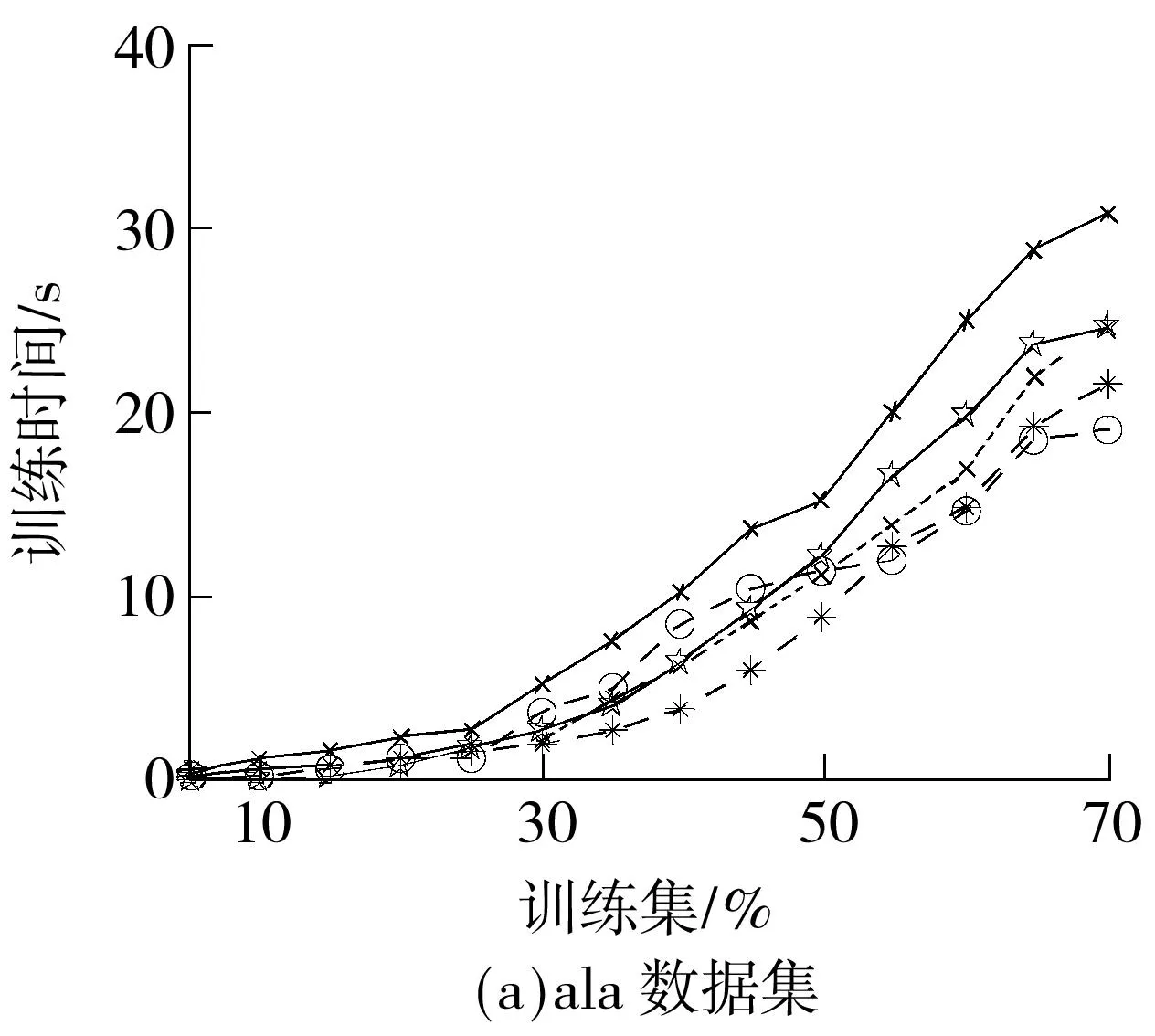
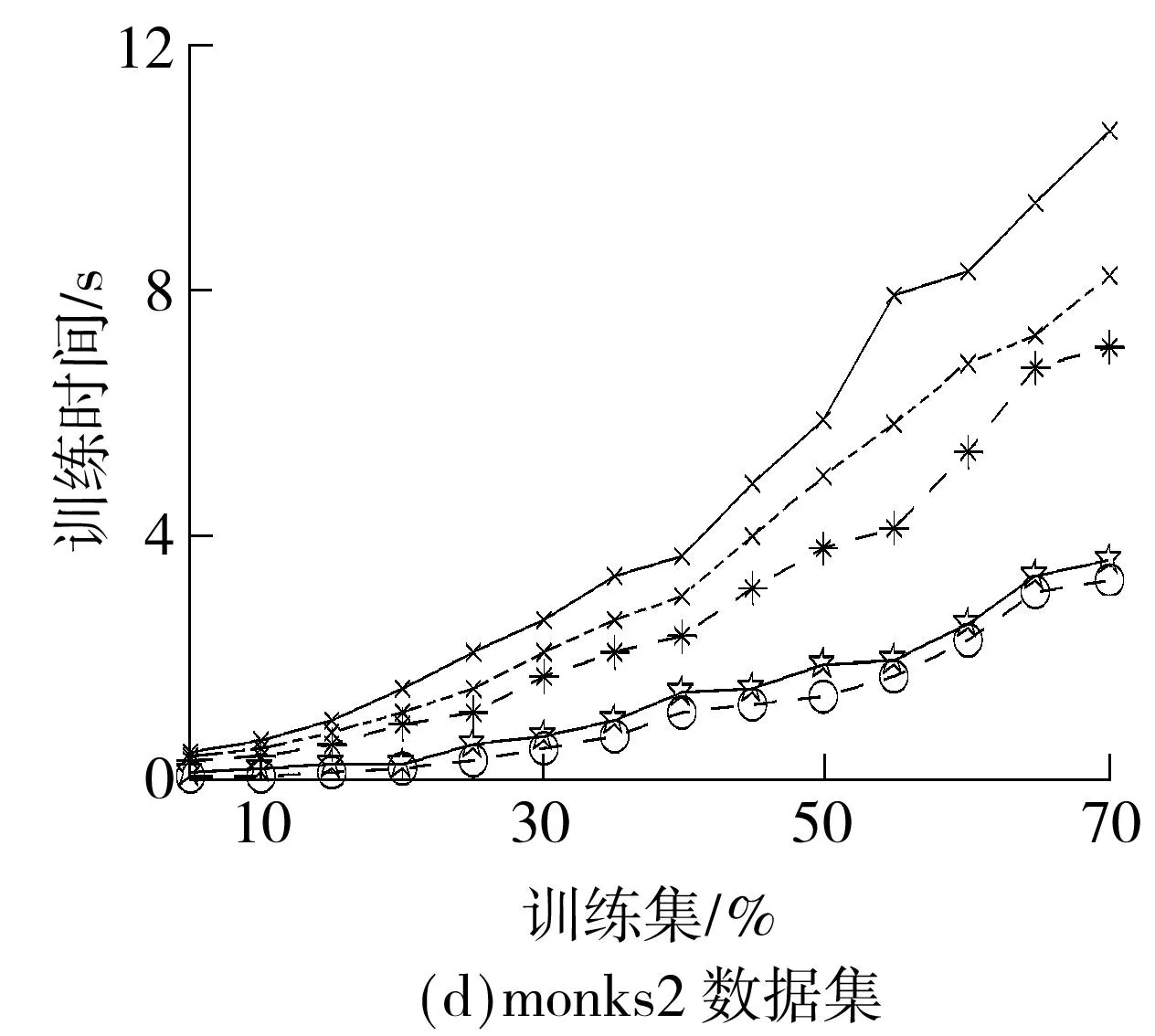
(2)训练时间比较

训练时间不包含Gram矩阵的生成时间.实验针对每种情况运行10次求平均,最后得到在6个数据集上5种算法的训练时间与训练集大小之间的关系,如图2所示.可以看出,LP-MKL在所有数据集上的训练时间最长,这说明非稀疏的多核学习方法的收敛速度相对较慢.稀疏多核学习方法SimpleMKL 和HessianMKL的训练时间比较接近,但SimpleMKL的训练时间要比HessianMKL稍长,这是由于两者在计算权系数时,分别采用了梯度投影和二阶牛顿法,后者有更快的收敛速度.PrimalMKL的训练时间波动比较大,在monks2、pima及wdbc数据集上表现较好,而在其他数据集上表现稍差.虽然QN-MKL获得权系数的非稀疏解,但由于采用了拟牛顿法求解SVM,故相对于其他算法有更快的收敛速度,在大多数据集上花费的训练时间有明显的降低.

(3)权系数的收敛趋势

为便于绘图,本实验选择了7个高斯核(σ分别为2-3,2-2,…,22,23),P=6,两步优化的迭代次数与权系数θm的收敛趋势如图3所示.从图中可以知道,文中算法迭代10次左右后趋于收敛,收敛过程非常平稳,并且绝大多数情况下总的迭代次数小于10,这表明文中算法具有很好的收敛性.

　

　

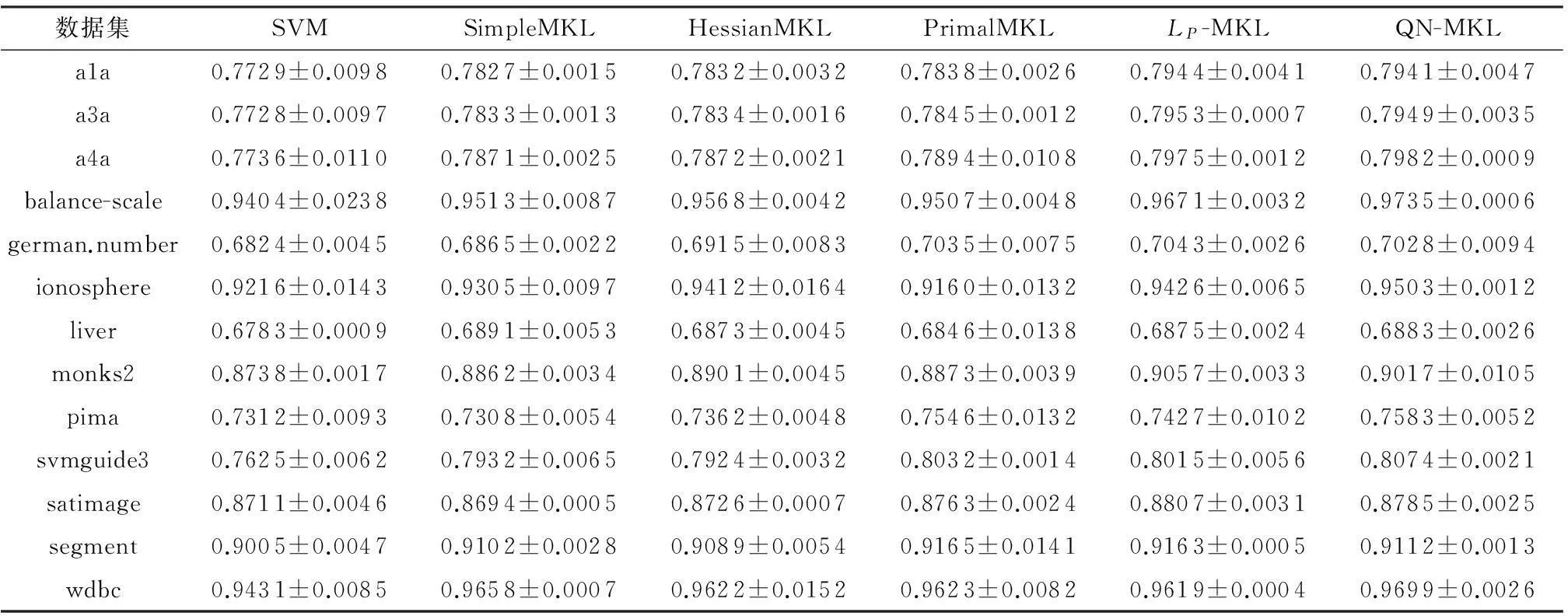
数据集SVMSimpleMKLHessianMKLPrimalMKLLP-MKLQN-MKLa1a0.7729±0.00980.7827±0.00150.7832±0.00320.7838±0.00260.7944±0.00410.7941±0.0047a3a0.7728±0.00970.7833±0.00130.7834±0.00160.7845±0.00120.7953±0.00070.7949±0.0035a4a0.7736±0.01100.7871±0.00250.7872±0.00210.7894±0.01080.7975±0.00120.7982±0.0009balance-scale0.9404±0.02380.9513±0.00870.9568±0.00420.9507±0.00480.9671±0.00320.9735±0.0006german.number0.6824±0.00450.6865±0.00220.6915±0.00830.7035±0.00750.7043±0.00260.7028±0.0094ionosphere0.9216±0.01430.9305±0.00970.9412±0.01640.9160±0.01320.9426±0.00650.9503±0.0012liver0.6783±0.00090.6891±0.00530.6873±0.00450.6846±0.01380.6875±0.00240.6883±0.0026monks20.8738±0.00170.8862±0.00340.8901±0.00450.8873±0.00390.9057±0.00330.9017±0.0105pima0.7312±0.00930.7308±0.00540.7362±0.00480.7546±0.01320.7427±0.01020.7583±0.0052svmguide30.7625±0.00620.7932±0.00650.7924±0.00320.8032±0.00140.8015±0.00560.8074±0.0021satimage0.8711±0.00460.8694±0.00050.8726±0.00070.8763±0.00240.8807±0.00310.8785±0.0025segment0.9005±0.00470.9102±0.00280.9089±0.00540.9165±0.01410.9163±0.00050.9112±0.0013wdbc0.9431±0.00850.9658±0.00070.9622±0.01520.9623±0.00820.9619±0.00040.9699±0.0026

　

　

　

　

　

　

(5)基本核的可扩展性

本实验验证基本核个数对训练时间的影响,选择了4个数据集,基本核的个数分别在1～17取值,随机选择50%的样本进行训练,执行10次求平均,最后得到训练时间与基本核个数之间的关系,如图5所示.除数据集monks2以外,随着M的增加,训练时间基本上呈线性变化,这表明了文中算法有较好的可扩展性,可适用于大规模的核学习.

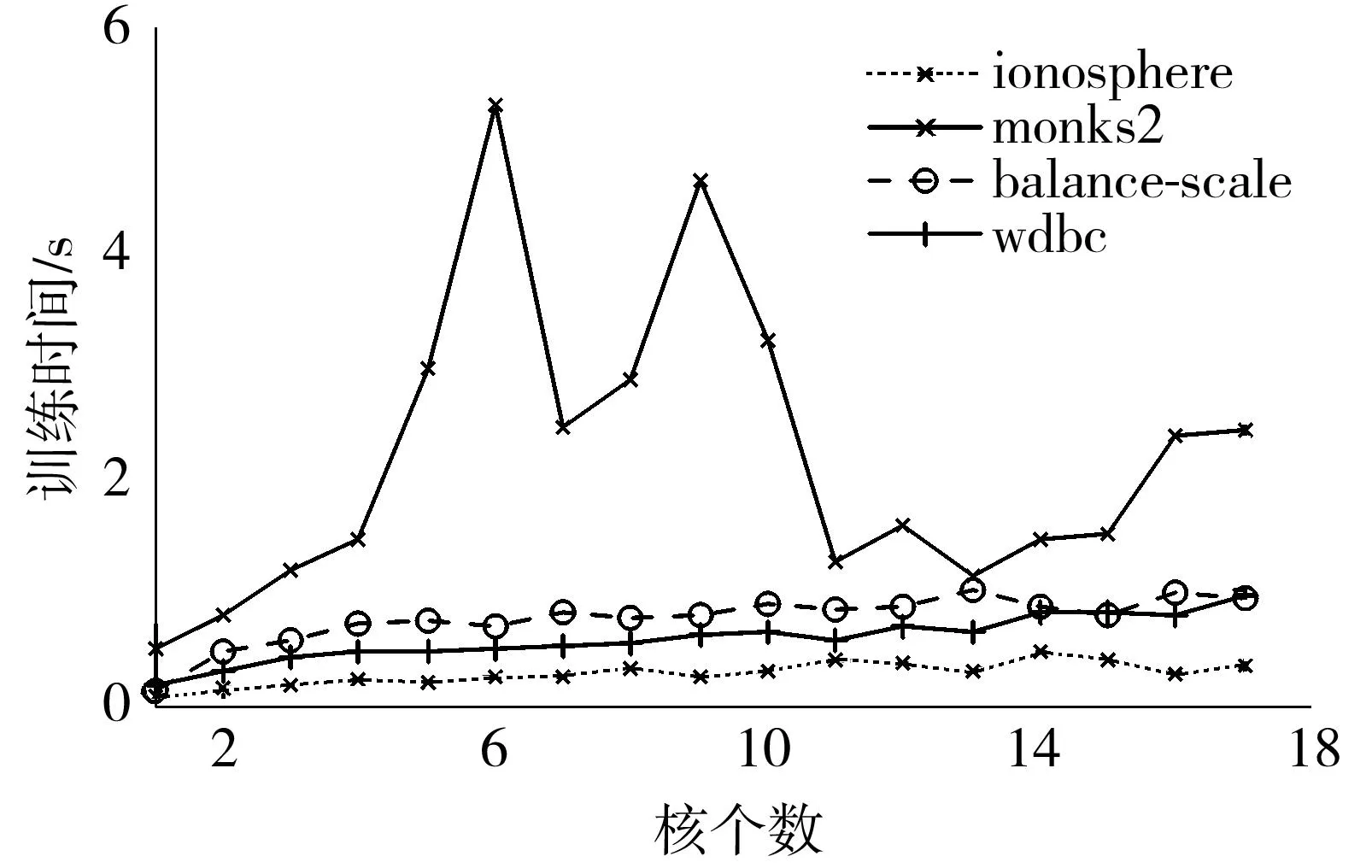
图5　基本核个数对训练时间的影响

Fig.5Influence of the total number of basic kernels on training time

4结论

文中提出了一种非稀疏多核学习算法,在原问题上分别采用两步优化方法对SVM和权系数进行求解.在优化SVM时,利用了次梯度和改进的拟牛顿法解决模型的非平滑问题.实验结果表明:QN-MKL与非稀疏多核学习算法LP-MKL有相似的分类精度,但QN-MKL的训练时间要远远小于LP-MKL;相比于L1范数约束的算法,在绝大多数数据集上QN-MKL的分类精度表现得更好且训练时间较少,这主要得益于非稀疏核组合的优点及拟牛顿法的超线性收敛属性;文中算法具有较好的收敛性和可扩展性.今后拟将文中算法扩展到半监督多核学习的框架.

参考文献：

[1]Bach F R.Consistency of the group lasso and multiple kernel learning [J].Journal of Machine Learning Research,2008,9(6):1179-1225.

[2]Zheng D N,Wang J X,Zhao Y N.Non-flat function estimation with a multi-scale support vector regession [J].Neurocomputing,2006,70(13):420-429.

[3]Ong C S,Smola A J,Williamson R C.Learning the kernel with hyperkernels [J].Journal of Machine Learning Research,2005,6(7):1043-1071.

[4]Lanckriet B G,Jordan M.Multiple kernel learning,conic duality,and the SMO algorithm [C]∥Proceedings of the 21th International Conference on Machine Learning.Banff:ACM,2004:41-48.

[5]傅贵,韩国强,逯峰,等.基于支持向量机回归的短时交通流预测模型 [J].华南理工大学学报:自然科学版,2013,41(9):71-76.

Fu Gui,Han Guo-qiang,Lu Feng,et al.Short-term traffic flow forecasting model based on support vector machine regression [J].Journal of South China University of Techno-logy:Natural Science Edition,2013,41(9):71-76.

[6]Rakotomamonjy A,Bach FR,Canu S,et al.SimpleMKL [J].Journal of Machine Learning Research,2008,9(11): 2491-2521.

[7]Chapelle O,Rakotomamonjy A.Second order optimization of kernel parameters [C]∥Proceedings of the 21th Advances in Neural Information Processing Systems Workshop on Kernel Learning:Automatic Selection of Optimal Kernels.Vancouver:MIT Press,2008:1-4.

[8]Gönen Mehmet,Alpayd1n Ethem.Multiple kernel learning algorithms [J].Journal of Machine Learning Research,2011,12(7):2211-2268.

[9]Xu Z,Jin R,King I,et al.An extended level method for efficient multiple kernel learning [C]∥Proceedings of the 21th Neural Information Processing Systems.Vancouver:MIT Press,2008:1825-1832.

[10]Kloft M,Brefeld U,Laskov P,et al.Non-sparse multiple kernel learning [C]∥Proceedings of the Workshop on Kernel Learning:Automatic Selection of Optimal Kernels.Whistler:MIT Press,2008:1-4.

[11]Kloft M,Brefeld U,Sonnenburg S,et al.LP-norm multiple kernel learning [J].Journal of Machine Learning Research,2011,12(5):953-997.

[12]汪洪桥,孙富春,蔡艳宁,等.多核学习方法 [J].自动化学报,2010,36(8):1037-1050.

Wang Hong-qiao,Sun Fu-chun,Cai Yan-ning,et al.On multiple kernel learning methods [J].Acta Automatica Sinica,2010,36(8):1037-1050.

[13]Longworth C,Gales M J F.Combining derivative and pa-rametric kernels for speaker verification [J].IEEE Tra-nsactions on Audio,Speech and Language Processing,2009,17(4):748-757.

[15]Das S,Matthews B L,Srivastava A N,et al.Multiple kernel learning for heterogeneous anomaly detection: algorithm and aviation safety case study [C]∥Proceedings of the 16th International Conference on Knowledge Discovery and Data Mining.Washington: ACM,2010:47-56.

[16]Lanckriet G R G,Cristianini N,Bartlett P,et al.Learning the kernel matrix with semi-definite programming [J].Journal of Machine Learning Research,2004,5(1): 27-72.

[17]Sonnenburg S,Ratsch G,Schafer C,et al.Large scale multiple kernel learning [J].Journal of Machine Lear-ning Research,2006,7(7):1531-1565.

[18]Melacci S,Belkin M.Laplacian support vector machines trained in the primal [J].Journal of Machine Learning Research,2011,12(5):1149-1184.

[19]Hao Zhifeng,Yuan Ganzhao,Yang Xiaowei,et al.A primal method for multiple kernel learning [J].Neural Computer & Application,2013,23(3/4):975-987.

[20]Liang Zhizheng,Xia Shixiong,Zhou Yong,et al.TrainingLPnorm multiple learning in the primal [J].Neural Network,2013,46(7):172-182.

[21]Yu J,Vishwanathan S V N,Gunter S,et al.A quasi Newton approach to nonsmooth convex optimization problems in machine learning [J].Journal of Machine Learning Research,2010,11(5):1145-1200.

[22]Kimeldorf G,Wahba G.Some results on tchebycheffian spline functions [J].Journal of Mathematical Analysis,1971,33:82-95.

A Non-Sparse Multi-Kernel Learning Method Based on Primal Problem

HuQing-hui1,2DingLi-xin1LiuXiao-gang2LiZhao-kui1

(1.School of Computer∥State Key Laboratory of Software Engineering,Wuhan University,Wuhan 430072,Hubei,China;

2.Guangxi Colleges and Universities Key Laboratory Breeding Base of Robot and Welding Technology,

Guilin University of Aerospace Technology,Guilin 541004,Guangxi,China)

Abstract:Traditional multi-kernel learning (MKL) methods mainly solve primal problems in the dual. However, the solving in the primal may result in better convergence property. In this paper, a novel Lp-norm-constraint non-sparse MKL method, which optimizes the modal in the primal, is proposed. In this method, firstly, support vector machine (SVM) is solved by means of subgradient and improved quasi-Newton method. Then, basic kernel weights are obtained via simple calculations. As quasi-Newton method is of second-order convergence property and acquires inverse Hessian matrix without computing the second-order derivative, the proposed method is of higher convergence speed than that of conventional ones. Simulated results show that the proposed method is of comparable classification accuracy, strong generalization capability, high convergence speed and good scalability.

Key words: multi-kernel learning; quasi-Newton method; alternating optimization; support vector machines