巧借东风，化难为易——一个基本图形在中考复习中的应用

王雪丽

（浙江省温岭市松门镇中学）

巧借东风，化难为易
——一个基本图形在中考复习中的应用

王雪丽

（浙江省温岭市松门镇中学）

在历年的中考题中，以加菲尔德证明勾股定理时所采用的构图为基础进行演变，形成一类基本图形，结合平行四边形、平面直角坐标系、函数知识的综合题目，它们都可由两个三角形相似得到相应的边之间的关系，从而进行解题。引导学生注重对已获得的知识、解题经验进行归纳和转化，进一步发展解题能力，提高中考复习的有效性。

构造；加菲尔德图形；相似三角形

美·波利亚说：“求解某个数学题目所需的材料是我们以前所获得的数学知识中某些与之相关的内容，比如以前解过的某些题目或者以前证明过的某些定理。”应用一些基本图形及基本结论可以提高学生相应的解题能力。

1876年，美国第20任总统詹姆斯·琼·加菲尔德（A·Garfield, 1831～1881），他在《新英格兰教育日志》上发表了勾股定理的证明，如图1，通过构造两个全等的直角三角形，利用同一图形整体面积等于局部面积之和，从而证明了勾股定理。惊叹于证明的巧妙构思之余，更对于他的构图产生了一些思考。

如图1，已知∠B=∠D=∠ACE=90°可得∠ECD=∠CAB，所以△ABC～△ECD，若两个三角形的相似比为1，则△ABC≌△ECD。

图1

如图1这样的基本图形，我们称之为加菲尔德图形，也叫做三垂足共线图形。从上述的证明中我们发现加菲尔德图形有个基本结论，若∠B=∠D=∠ACE=90°，则△ABC～△ECD。

这一基本图形的基本结论在中考题中有较广泛的应用，特别在求线段长度、点的坐标以及函数等问题时，应用这一基本图形，可达到事半功倍的效果。

一、在有些数学题中直接提炼加菲尔德图形，应用基本图形的结论构造方程求解

例1（.2014年山东省枣庄市）如图2，将矩形ABCD沿CE向上折叠，使点B落在AD边上的点F处，若AE=BE，则长AD与宽AB的比值是_______。

图2

二、在很多数学题中，加菲尔德图形是隐性存在的，这就需要学生在解题过程中去构造加菲尔德图形

图3

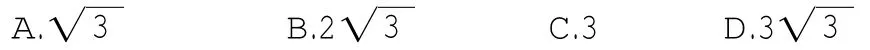
图4

图5

例3（.2014年江苏省南京市）如图5，在矩形AOBC中，点A的坐标是（-2，1），点C的纵坐标是4，则B、C两点的坐标分别是 （ ）

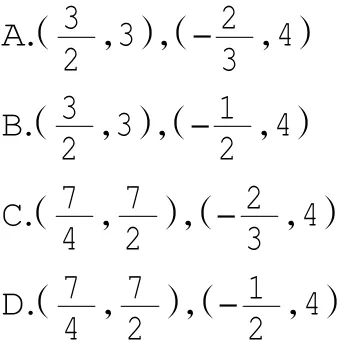
解析：求点的坐标常联想到过点作坐标轴的垂线段，从而求点坐标问题可转化为求垂线段的长度问题，如图6，过A、B、C分别作AD⊥x轴于点D，BE⊥x轴于点E，CG⊥y轴于点G,交BE于点F。构造两个加菲尔德图形，易得△DAO～△EOB～△FBC，又由于BC=AO，则△DAO≌△FBC，结合已知条件易得，OE=，CG=。故选B。

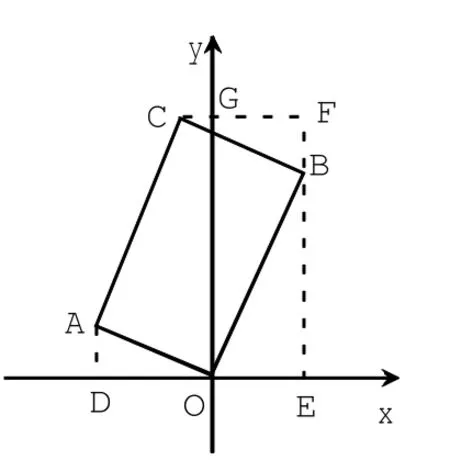
图6

分解和重组是思维的重要活动。复杂的综合题是由一些常见的基本题目、基本图形组合而成的。对于这一类题目，我们可以采用庖丁解牛的手法，把复杂的问题分解成简单的问题；应用基本图形及其结论可使复杂的问题迎刃而解，这种化难为易、化繁为简的解题思想初中数学中考复习很重要。

三、迁移图形

当∠B=∠C=∠AED=a时，加菲尔德图形的结论仍成立。我们把类似于图7的基本图形叫做M型图形，也叫做三等角顶点共线图形。它们有共同结论：△ABC～△ECD。

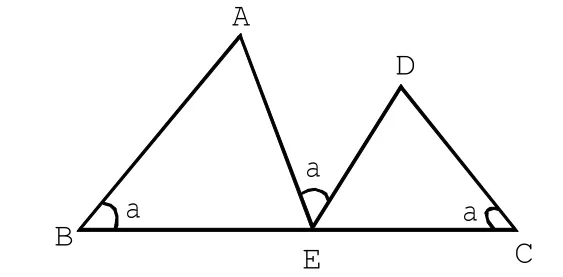
图7

引导学生熟悉和掌握一系列基本图形及其相关结论，能够把问题从陌生熟悉化，从复杂简单化，从困惑明朗化。引导学生注重对题目条件的分析、结论的分析，以及条件和结论之间联系的分析。归纳出解决问题的通性、通法，既能夯实基础，又能达到让学生懂一题，晓一类，通一片的效果。推动学生数学能力的发展和数学思维的进步，从而提高中考复习的有效性。

［1］波利亚.怎样解题：数学思维的新方法［M］.涂泓，冯承天，译.上海：上海科技教育出版社，2013.

［2］王金战，王志进.中考抢分36计：数学［M］.吉林教育出版社，2011.

·编辑 张珍珍