平直出口段对微喷管性能的影响
【基础理论与应用研究】
平直出口段对微喷管性能的影响
童军杰1,2,方运惠1,马晓茜2
(1.广州航海学院 船舶工程系,广州510725; 2.华南理工大学 电力学院, 广州510641)
摘要:以Fluent 6.3为工具,进行数值模拟求解二维稳态可压缩N-S方程,分析了喷管有无平直出口段以及平直出口段长度对扩张比为5.4的收缩-扩张微喷管内压力和速度分布影响,进而分析了对微喷管的流量系数和推力效率影响;计算结果表明:喷管有无平直出口段以及平直出口段长度l,将会影响微喷管出口区域流体压力分布和速度分布;与喷管出口无平直出口段相比,当喷管出口有平直出口段时,流体压力最低值和速度最大值靠近喷管出口中心区域,并且影响区域增加;当喉部特征雷诺数Re较小时,流量系数Cd和推力系数ηF随l的增加先增大再减小;随着Re的增加,流量系数Cd和推力系数ηF的变化变小。
关键词:模拟;微喷管;出口段;推力;流量
收稿日期:2014-07-12
基金项目:国家重点基础研究发展项目(2011CB201500); 广东省博士启动项目(1209386)
作者简介:童军杰(1976—),男,博士,副教授,主要从事能源与动力研究;
doi:10.11809/scbgxb2015.01.038
中图分类号:V430
文章编号:1006-0707(2015)01-0137-04
本文引用格式:童军杰,方运惠,马晓茜.平直出口段对微喷管性能的影响[J].四川兵工学报,2015(1):137-140.
Citation format:TONG Jun-jie, FANG Yun-hui,MA Xiao-qian.Impact on of Straight Outlet Section to Micro-Nozzle Performance[J].Journal of Sichuan Ordnance,2015(1):137-140.
Impact on of Straight Outlet Section to Micro-Nozzle Performance
TONG Jun-jie1,2, FANG Yun-hui1, MA Xiao-qian2
(1.Department of Ship Engineering, Guangzhou Maritime Institute, Guangzhou 510725, China;
2.School of Electric Power, South China University of Technology, Guangzhou 510641, China)
Abstract:The Fluent 6.3 software was applied to simulate the supersonic flow in micro nozzle. The simulation was complemented by computing steady 2-D Navies-stokes equations to analyze the pressure contour and velocity contour inside the micro nozzle which has straight exit section and the length of straight exit section l . Also the performances of flow coefficients and thrust force efficiencies were studied. The numerical results show that whether the nozzle has straight exit section or not and the section length l will affect the pressure contour and velocity contour inside the thruster. Compared to the nozzle that has no straight exit section, the increased minimum pressure region and the maximum velocity region are close to the center of exit in the nozzle that has straight exit section. When the throat Reynolds number Re is small, the flow coefficient Cd and thrust coefficient ηF firstly increase then decrease with the increase of l. With the increase of Re, the variation of the flow coefficient Cd and thrust coefficient ηF for higher Re are smaller than for lower Re.
Key words: simulation; micro-nozzle; outlet section; thrust; flow
微喷管主要用于微型航天器的精密调姿及轨道定位。由于尺度的微型化引起的低雷诺数和比表面积增大引起的下粘性损失增大带来的影响比常规尺度更为明显。对微喷管的几何结构设计将影响微喷管的性能参数。综合文献资料,有关几何结构对微喷管性能的影响的研究,主要包括:扩张角及其大小对微喷管推进性能的影响[1-4];喉部曲率半径及部队称性对微喷管推进性能的影响[5-7];喉部尺寸对微喷管性能影响[8]。
综合目前文献资料,关于微喷管出口几何结构对微喷管推进性能的影响研究,却很少有相关报道。为了研究喷管出口段几何结构对微喷管性能的影响,本文以Fluent 6.3软件为工具,研究了喷管有无平直出口段以及平直出口段长度,对微喷管流量系数与推力效率等推进性能的影响。
1物理模型
1.1微喷管的几何模型
本文基于Bayt[2]算例为参考,分析刻蚀深度远大于喉部宽度的微喷管,微喷管的形状及坐标系的建立如图1所示,各个尺寸如下:喷管进口宽度Win=80 μm,喉部宽度Wt=19 μm,半收缩角θ1=45°,半扩张角θ2=20°,几何扩张比Wout/Wt=5.4,喷管出口长度l=0~54 μm。
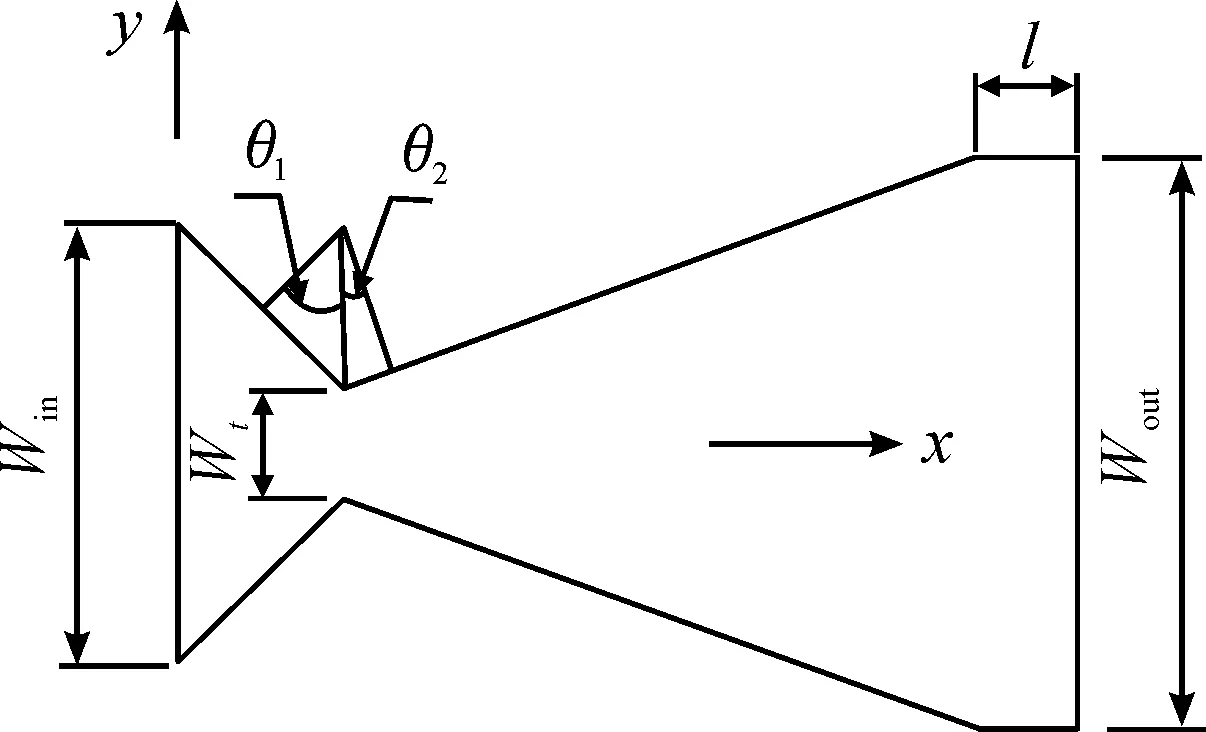
图1 微喷管几何外形示意图
1.2计算区域及网格划分
由于计算的微喷管是对称的,为了节省计算时间,因此在计算过程中,取其一半作为计算对象。考虑微喷管外流场对微喷管计算的影响,计算区域包含了喷嘴出口外的影响区域,计算区域和边界条件设定如图2所示。在计算区域内,采用四边形结构网格,在喷嘴喉部与壁面附近加密喷嘴外计算区域网格的数目为15 000,当喷管出口长度l分别为0、19 μm、38 μm、 54 μm和72 μm,喷嘴内计算区域网格的数目为15 600,16 680,17 760,18 840和19 920。
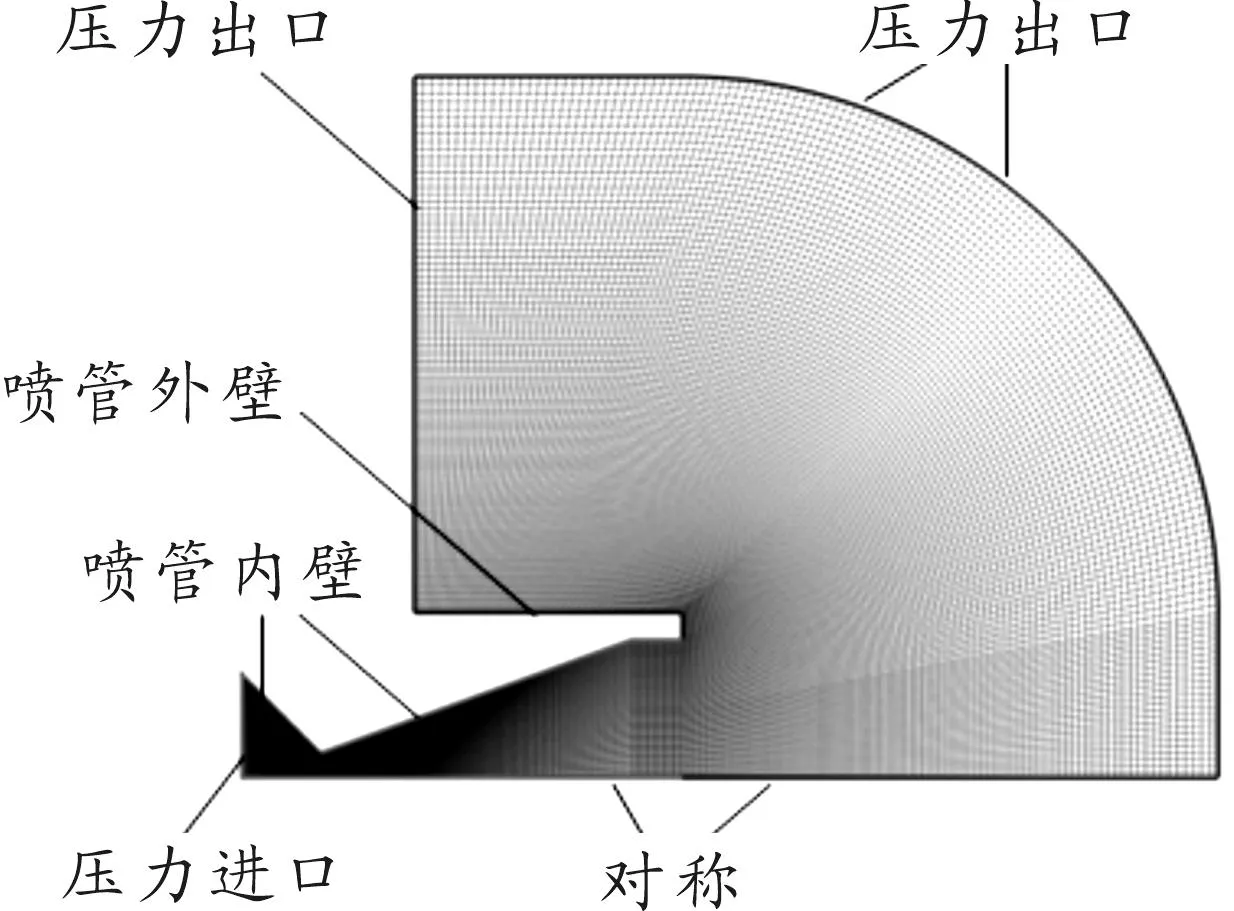
图2 计算区域及网格划分
1.3控制方程
考虑到微喷管内气体的稀薄效应,使用N-S方程结合一阶壁面滑移和温度跳跃边界条件,对喷管进行二维数值模拟N-S通用方程[9]
div(ρUΦ)=div(ΓgradΦ)+S
(1)
式(1)中:ρ为流体密度;U为流体速度矢量;Γ为广义扩散系数;S为广义源项;Ф为通用变量。通用控制方程涵盖了本文求解运用到的连续方程、动量方程和能量方程。
速度一阶壁面滑移边界条件[3]
(2)
壁面温度跳跃边界条件[3]为
(3)
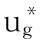
1.4物性参数及边界条件设置
微喷管中的流体为氮气,满足理想气体状态方程,氮气动力黏度随温度的变化遵从sutherland[7]方程。
理想气体状态方程
pV=RgT
(4)
氮气动力粘度随温度的变化遵从sutherland[7]方程
(5)
其中:μ0为参考温度T0=273.11k时的动力粘度,在此对应的值为1.663×10-5kg/m·s;S1为常数106.67K。
流体入口设定为压力入口条件,在本文算例中,喷管喉部特征雷诺数Re分别为200、500、800、1 100、1 400、1 700和2 000,相对应喷管进口压力p*分别为0.71bar、1.78bar、2.85bar、3.91bar、4.98bar、6.05bar和7.12bar,流体出口压力设定为20Pa,模拟流体出口为较高真空度的微喷管的流动。
喉部特征雷诺数Re为准一维理想等熵膨胀时喷管喉部的雷诺数,用来表示喷管内流体流动时惯性力的相对大小
(6)
其中:ρt,ut,μt和Lt为准一维等熵膨胀时喷管喉部处y方向截面平均密度,平均速度,平均动力粘度和喉部特征长度,
在喷管进出口几何尺寸不变的情况下,喉部特征雷诺数Re越大,喷管进口压力越大,喷管流量越大,喷管内部流动惯性力也越大。
2计算结果及讨论
2.1计算方法验证
通过计算,本文所有算例微喷管的流场Kn值均小于0.03,满足N-S方程结合一阶壁面滑移边界条件和温度跳跃条件假设的正确性。其中Kn定义为平均自由程λ与特征几何长度D的比值。
2.2流场计算结果
对于流场计算结果,选取喉部特征雷诺数为1400,喷管出口平直长度为0μm与38μm的流场进行分析。图3和图4 分别为喉部特征雷诺数为1 400,喷管出口平直长度l为 0μm的静压力分布和流速分布对y轴进行镜像,并与相应的喷管出口平直长度l为0μm静压力分布和流速分布在喷管出口处进行拼接得出来的流场图。
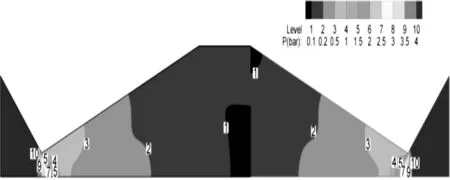
图3 Re=1 400时平直长度l=38 μm
从图3中可以看出,对于平直长度l=38μm和 l=0μm,在喷管内大部分区域,喷管内的压力分布大致相等。在喷管出口附近,压力分布出现明显变化,当喷管出口平直长度l=38μm时,喷管内的压力最低值靠近喷管出口中心区域;相比较平直长度l=38μm,当喷管出口平直长度l=0μm时,喷管内的压力最低值靠近壁面附近,喷管内的压力最低值区域减小。
从图4中可以看出,对于平直长度l=38μm和 l=0μm,在喷管内大部分区域,喷管内的速度分布大致相等。在喷管出口附近,速度分布出现明显变化,当喷管出口平直长度l=38μm时,喷管内的压力最低值靠近喷管出口中心区域;相比较平直长度l=38μm,当喷管出口平直长度l=0μm时,喷管内的速度最大值区域向壁面附近靠近,喷管内的速度最大值区域减小。
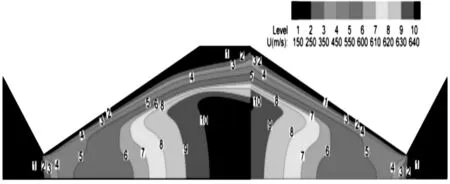
图4 Re=1 400时平直长度l=38 μm 和
2.3性能计算结果
图5为微喷管流量系数在不同喉部特征雷诺数下随喷管出口平直长度的变化规律图。图6为微喷管推力效率在不同喉部特征雷诺数下随喷管出口平直长度的变化规律图。
其中,流量系数Cd为二维喷管流体的流量与相应不考虑粘性的理想气体的准一维喷管的流量比值。推力系数ηF为二维喷管出口的x方向推力大小与相应的不考虑粘性的理想气体准一维情况下喷管出口的推力大小比值。
从图5中可以看出,当Re较小时,随着喷管出口平直长度l的增加,流量系数Cd随l的增加先增大再减小。随着Re的增加,流量系数的变化较小。
从图6中可以看出,当Re较小时,随着喷管出口平直长度l的增加,推力系数ηF随l的增加先增大再减小。随着Re的增加,推力系数的变化较小。
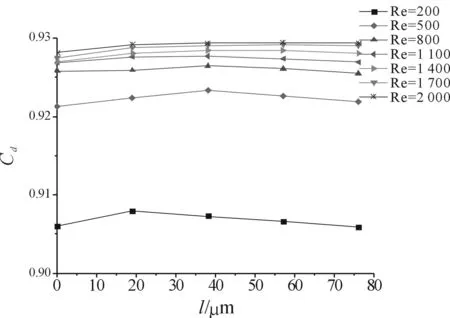
图5 Re=200~2 000时流量系数 C d随l变化
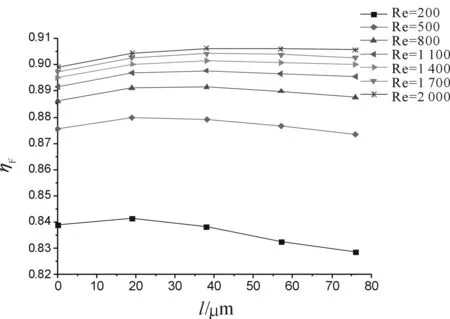
图6 Re=200~2 000时推力系数 η F随l变化
2.4分析与讨论
1) 与喷管出口无平直出口段比较,当喷管出口有平直出口段时,在喷管出口附近,压力分布出现明显变化,喷管内的压力最低值靠近喷管出口中心区域;同时,喷管内的压力最低值区域增加。
分析认为,在喷管出口壁面附近,由于喷管出口平直段对流体的挤压与约束,使得壁面处附近流体压力得到部分补偿,因而喷管内的压力最低值靠近喷管出口中心区域。同时,由于在平直出口段,流体继续膨胀,压力继续降低,因而喷管内的压力最低值区域增加。
2) 与喷管出口无平直出口段比较,当喷管出口有平直出口段时,在喷管出口附近,速度分布出现明显变化,喷管内的速度最大值区域靠近中心处,喷管内的速度最大值区域增加。
分析认为,在喷管出口壁面附近,由于喷管出口平直段对流体的挤压与约束,使得壁面处流体偏向中心区域流动。因而喷管内的速度最大值区域靠近中心处。
同时,由于在平直出口段,流体继续膨胀,速度继续增加,因而喷管内的速度最大值区域增加。
3) 当Re较小时,随着喷管出口平直长度l的增加,流量系数Cd随l的增加先增大再减小。随着Re的增加,流量系数的变化较小。
分析认为,在喷管出口壁面附近,由于喷管出口平直段对流体的挤压与约束,喷管出口处流体流向偏离x方向的发散度减小。因而,适当的喷管出口长度将提高流量系数Cd。
当Re较小时,随着喷管出口平直长度l的增加,粘滞阻力的影响增加,因而较大的喷管出口长度l使得流量系数Cd减小。
4) 当Re较小时,随着喷管出口平直长度l的增加,推力系数ηF随l的增加先增大再减小。随着Re的增加,推力系数的变化较小。
分析认为,在喷管出口壁面附近,由于喷管出口平直段对流体的挤压与约束,喷管出口处流体流向偏离x方向的发散度减小,喷管出口x方向的推力增加,因而,适当的喷管出口长度将提高喷管的推力。
当Re较小时,随着喷管出口平直长度l的增加,粘滞阻力的影响增加,因而喷管出口的推力将减小。
3结论
通过数值计算分析了喷管出口接近真空环境下,分析了喷管有无平直出口段以及平直出口段长度l对扩张比为5.4的收缩-扩张微喷管内压力和速度分布影响,进而分析了对微喷管的流量系数和推力效率影响。
与喷管出口无平直出口段比较,当喷管出口有平直出口段时,在喷管出口附近,压力分布和速度分布出现明显变化,喷管内的压力最低值和速度最大值靠近喷管出口中心区域,其影响区域增加。 当Re较小时,随着喷管出口平直长度l的增加,流量系数Cd和推力系数ηF随l的增加先增大再减小,随着Re的增加,流量系数Cd和推力系数ηF变化较小。
参考文献:
[1]KimSC.Calculationsoflow-Reynolds-numberresistojetnozzles[J].JournalofSpacecraftandRocket,1994,31(2):259-264.
[2]BaytRLAnalysis,FabricationandTestingofaMEMS-basedMicropropulsionSystem[D].Ph.D.Dissertation,MIT,Cambridge.
[3]张根烜.基于多孔介质内燃烧的微小型化学推进系统的数值研究[D].北京:中国科学技术大学,2006.
[4]WangMR,LiZX,NumericalsimulationsonperformanceofMems-basednozzlesatmoderateorlowtemperatures[J].MicrofluidicsandNanofluidcs,2004(1):62-70.
[5]IvanovMS,MarkelovGN.Numerialstudyofcoldgasmicronozzleflows.AIAA99-0166.
[6]童军杰,徐进良.喉部结构对微喷管性能的影响[J].航空动力学报, 2009,24(5):15-19.
[7]WangMR,LiZX.NumericalsimulationsonperformanceofMems-basednozzlesatmoderateorlowtemperatures[J].MicrofluidicsandNanofluidcs,2004(1):62-70.
[8]王福军.计算流体动力学分析[M].北京:清华大学出版社,2004:7-13.
(责任编辑蒲东)


