导弹贮存可靠性试验中右删失数据的分布选择方法

【后勤保障与装备管理】

导弹贮存可靠性试验中右删失数据的分布选择方法

刘天放1，吴进煌2，刘海波2，唐培锋3

(1.海军航空工程学院 研究生管理大队，山东 烟台264001； 2. 91872部队，北京102442；

3. 91980部队，山东 烟台264000)

摘要：针对导弹贮存可靠性试验中右删失数据在数据处理时分布未知的问题，提出了一种分布选择方法。以右删失数据的PL估计作为数据分布选择的基准，计算常见分布下的参数估计，得到可靠度函数估计，计算各分布下可靠度函数曲线与PL估计曲线间的拟合距离，选取拟合距离最小的分布作为数据的拟合分布。

关键词：右删失；参数估计；PL估计；分布类型

收稿日期：2014-08-02

作者简介：刘天放(1988—)，男，硕士研究生，助理工程师,主要从事装备综合保障研究。

doi:10.11809/scbgxb2015.01.026

中图分类号：E927

文章编号：1006-0707(2015)01-0091-04

本文引用格式：刘天放，吴进煌，刘海波，等.导弹贮存可靠性试验中右删失数据的分布选择方法[J].四川兵工学报，2015(1):91-94.

Citationformat:LIUTian-fang,WUJin-huang,LIUHai-bo,etal.ProcessingMethodofRightCensoredDataDistributioninStorageReliabilityTest[J].JournalofSichuanOrdnance,2015(1):91-94.

ProcessingMethodofRightCensoredDataDistribution

inStorageReliabilityTest

LIUTian-fang1, WU Jin-huang2, LIU Hai-bo2, TANG Pei-feng3

(1.GraduateStudents’Brigade,NavalAeronauticalandAstronauticalUniversity,Yantai264001,China;

2.The91872ndTroopsofPLA,Beijing102442,China; 3.The91980thTroopsofPLA,Yantai264000,China)

Abstract:For the right censored data distribution is unknown in data processing, we proposed a distribution method. Took the loss of data PL estimates as the data distribution selecting reference to right censored, we calculated the parameter estimation under common distribution, then got the reliability function estimation, and calculated the distance between the fitting curve of the reliability function curve and PL to estimate the distribution and to select distribution fitting the minimum distance distribution as the data fitting.

Keywords:rightcensored;parameterestimation;PLestimation;distributiontype

导弹贮存可靠性是导弹在规定的条件下和规定的时间内贮存时，保持规定功能的能力[1]。导弹是长期贮存，一次使用的复杂系统，在其寿命周期内的主要状态是贮存[2]，导弹在经过贮存、维修后，其可靠性一般会降低[3]，因此要对导弹开展贮存可靠性试验来验证各项指标，并对得到的可靠性数据进行分析处理。导弹可靠性试验通常采用截尾寿命试验的方法进行，而导弹可靠性数据分布参数研究需要依靠大量的试验数据分析。

目前在导弹贮存可靠性试验中用截尾寿命试验法所得数据以右删失数据为常见数据类型，使用常用的数据分析方法所包含的信息严重不足，完全观测数据中所使用的分布选择方法用在右删失数据处理中会发生偏差，并不适用，针对此类数据的实用处理方法研究较少。本文针对导弹贮存可靠性试验中的右删失数据分布选择方法较少，提出以右删失数据的PL估计为基准分布曲线估计，从常用的指数、Weibull和正态等常见寿命分布中，选择与PL估计最接近的参数分布作为数据拟合的分布，为导弹可靠性工程中的数据分布选择工作提供一种实用方法，为导弹贮存可靠性试验中的可靠性评估提供技术支持。

1右删失数据的含义

从一定批量的产品中抽取一些试验样品(n个)做试验。当失效判据明确后，可以得到数据(t,n,r)，其中t为贮存年限，n为试验数，r为失效数。这组数据的特点是：① 成功数(n-r)是在t时刻试验时的成功数量，而其贮存寿命T(在这n-r中T>t)到底有多长是未知的；② 当r=0，即无失效数据时，其寿命有多长也是未知的[4]；③ 一般r≤n，特别当r=n时，截尾寿命试验就成为完全寿命试验。所以完全寿命试验是截尾寿命试验的一个极端情况。一般说来截尾样本所含的失效信息总比完全样本少一些，上述数据属于统计学中的生存分析。

生存分析理论研究的对象为非负随机变量T，即根据观测到的数据进行统计推断。生存分析的一大特点，就是讨论含有删失(或区间型)数据的情形。生存分析中常见的有3种类型的数据，包括右删失数据、左删失数据[5]和区间数据。右删失数据是生存分析中一种常见的数据类型。在进行观测试验或者调查时，产品已经发生故障，故障时间明确知道，属于完全观测；如果不知道一个个体的确切寿命，只知道其寿命大于某个值，则称该个体的寿命是右删失的[6]。定时截尾试验是可靠性试验中常用的试验方法，是指试验到指定时间就立即停止试验。而右删失数据在定时截尾试验中出现较为普遍，这时样本中的失效个数是随机的。譬如对40个样品进行寿命试验，事先指定1 000h是试验停止时间，那在1 000h内可能失效15个,也可能失效10个，样品具体寿命不得知，该样品的寿命所得数据即为右删失数据。在工程和医学领域经常出现右删失数据，比如接受过某种治疗的病人的寿命，如果只知道其治疗几年后还健在，则是右删失数据。右删失数据也是导弹使用和试验中常见的一类数据，用定时截尾试验方法得到的导弹贮存可靠性试验中的寿命数据通常并不完全，在试验期间某些故障和缺陷没有完全暴露出来，也就无法准确地反映导弹贮存可靠性的真实状态，因此，导弹在贮存可靠性试验期间各单元元器件所得的右删失型数据的分析对于准确评估导弹贮存可靠性有十分重要的意义。

2右删失数据的分布选择方法

2.1右删失数据的参数估计方法

右删失数据每个数据一般包括2个参数，时间和失效标记，类似结构如表1所示。0代表在这个时间点试件失效，而1代表在这个时间点试件右删失。

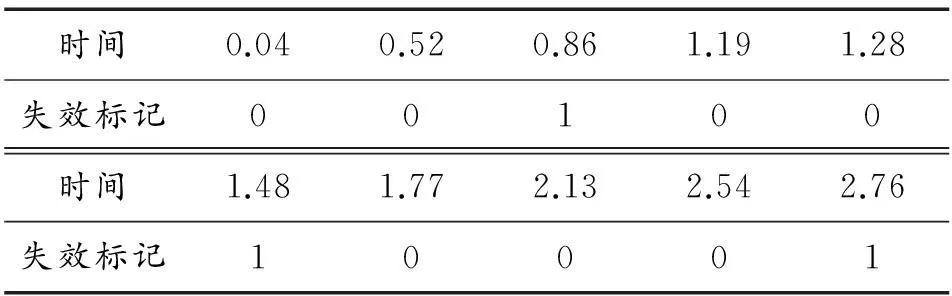
表1　右删失数据结构

在研究对象的分布函数类型完全未知时，生存分析理论针对不同类型的数据有着不同的分析方法，包括寿命表法、PL估计与Turnbull估计。寿命表法需要所分析对象的观测例数较多并分组[7]，这就需要研究的个体在各检测时刻同时进行检测，以确定个体在哪个区间中寿终或右删失，但这与导弹在部队的实际检测情况不相符合。Turnbull估计是针对区间型数据提出的估计方法[8]。右删失数据有几种重要的估计方法，如Product-Limit估计、Nelson-Alan估计、Pererson估计、Breslow估计等都是近几年应用较为广泛的概念，Product-Limit估计最早由Kaplan和Meier提出，因而又叫K-M估计[9]。由于它具有乘积极限的形式，称为乘积限估计。它在生存分析中的地位与经验分布函数在经典统计中的地位相仿，并且两者有相似的渐近性质：相合性、正态性等。模型公式如下

(1)

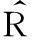
对右删失数据估计的方法，除了Product-Limit估计还有很多种，本文使用PL估计作为对右删失数据的估计方法。

2.2PL估计的理论基础

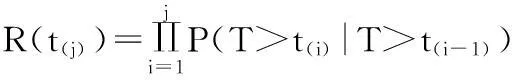
3右删失数据分布选择的具体步骤

3.1数据类型

右删失数据分布选择方法的思路是将待选的分布与PL估计的结果进行对比，从中选取和PL估计相比偏差更小的分布作为最优分布。设右删失数据对n个同样产品的寿命进行观测，得到t1,t2,…,tn，当ti是确切故障，即完全观测时，令δi=0；当ti为右删失数据时，令δi=1。可记录为

(ti,δi),i=1,2,…,n

3.2分布选择步骤

由于试验时间的限制和试验条件的局限，收集到的导弹试验数据为右删失数据，得到数据后，首先计算右删失数据的PL估计，将其作为数据分布的基准，然后计算4种常见分布下的参数估计，进而得到可靠度函数估计，再计算各分布下可靠度函数曲线与PL估计曲线间的拟合距离，选取拟合距离最小的分布作为数据的拟合分布。具体过程如下：

第一步：将右删失数据(ti,δi)按照ti的值从小到大排列，记为

(t(i),δ(i)),i=1,2,…,n

其中，t(1)≤t(2)≤…≤t(n)，当t(i)是确切故障数据时，记δ(i)=0；当t(i)是右删失数据时，记δ(i)=1。

计算该产品可靠度函数R(t)的PL估计如式(1)。

第二步：利用极大似然估计确定常见寿命分布下的可靠度函数估计。常见寿命分布包括指数分布、Weibull分布、正态分布和对数正态分布等。

指数分布适用于具有恒定的故障率的产品、在损耗前进行定时维修的部件、由随机高应力所导致的故障部件以及寿命期内出现耗损的部件；正态分布适用于变压器、灯泡、轮胎磨损等；对数正态分布适用于半导体元器件、金属疲劳、绕组绝缘等；威布尔分布适用于陀螺、电动机、断路器、电子管、电位计、液压传动装置、齿轮、材料疲劳等[11]，常用寿命分布的密度函数表达式，如表2所示。

极大似然估计通过对样本的考察，认为待估参数最像是取什么值作为对参数的估计，其出发点是基于以下统计原理：在一次随机试验中，某一事件已经发生，比如已经得到某个具体的样本X1,X2,…,Xn，则必然认为发生该事件的概率最大[12]。利用极大似然估计得出各常用寿命分布的可靠度函数并做出各个分布估计的曲线图。

表2　指数分布相关性质

第三步：以PL估计曲线与常见分布估计曲线所围面积对两曲线间进行数据拟合，计算各分布下可靠度函数曲线与PL估计曲线间的拟合距离，如图1所示(图2中折线为PL估计曲线，曲线为常见分布下的可靠度估计曲线)，衡量该分布与PL估计间的偏差，选取拟合距离最小的分布作为数据的拟合分布。具体可用公式(2)计算

(2)

第四步：按照第三步，依次计算PL估计曲线与不同常见寿命分布下可靠度估计曲线的拟合距离，选取拟合距离最小的分布作为该右删失数据的拟合分布。

上述方法以右删失数据的PL估计为基准，以常见寿命分布下可靠度估计曲线与PL估计的拟合距离为衡量标准进行数据分布选择，该方法能够定量反映所选参数分布和右删失数据的偏差。

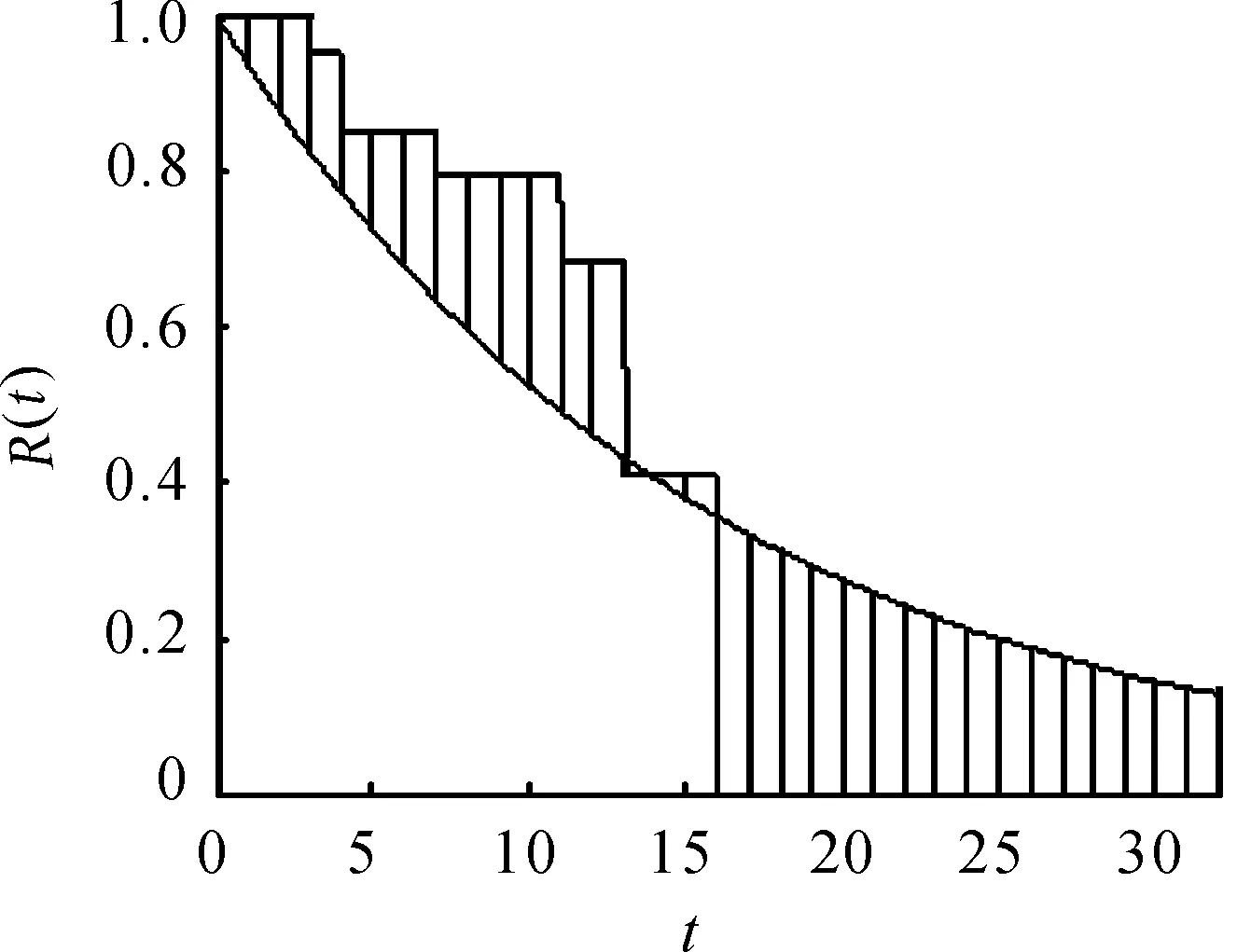
图1　常见分布估计曲线与 PL估计的拟合距离

4算例

某产品的实际贮存寿命记录，见表3，单位：天。试用上述方法，选择该数据的分布类型。

在表3中，第一行为失效时间，第二行为右删失标记，1为右删失，0为完全寿终。

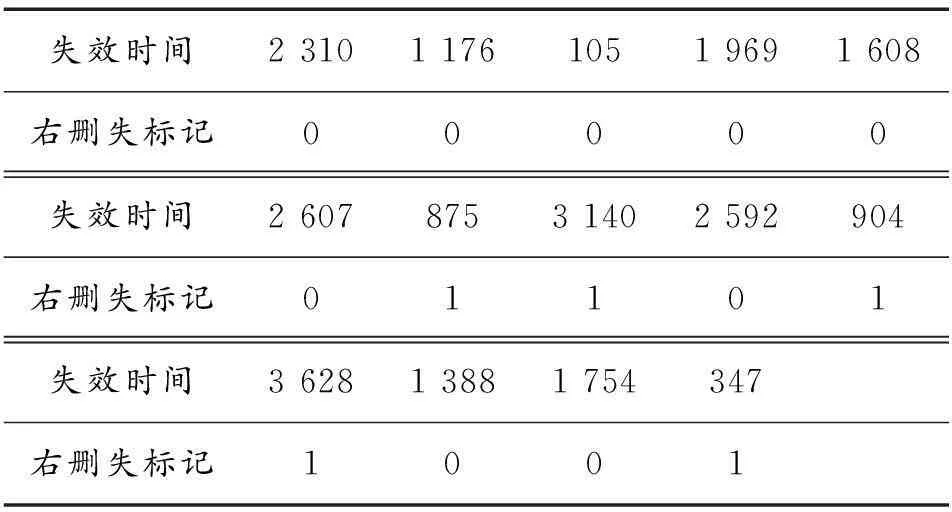
表3　某产品贮存失效记录

根据本文方法，绘制该右删失数据PL估计与常用寿命分布拟合曲线如图2所示，分别计算PL估计曲线与指数分布、威布尔分布、正态分布和对数正态分布拟合曲线间的面积，分别为：指数分布为1155.8，威布尔分布为340.95，正态分布为220.01，对数正态分布为1 609.1，见表4。从表4和图2，可以看出，正态分布的拟合效果最好，因此，选择正态分布作为该产品贮存寿命的拟合分布。

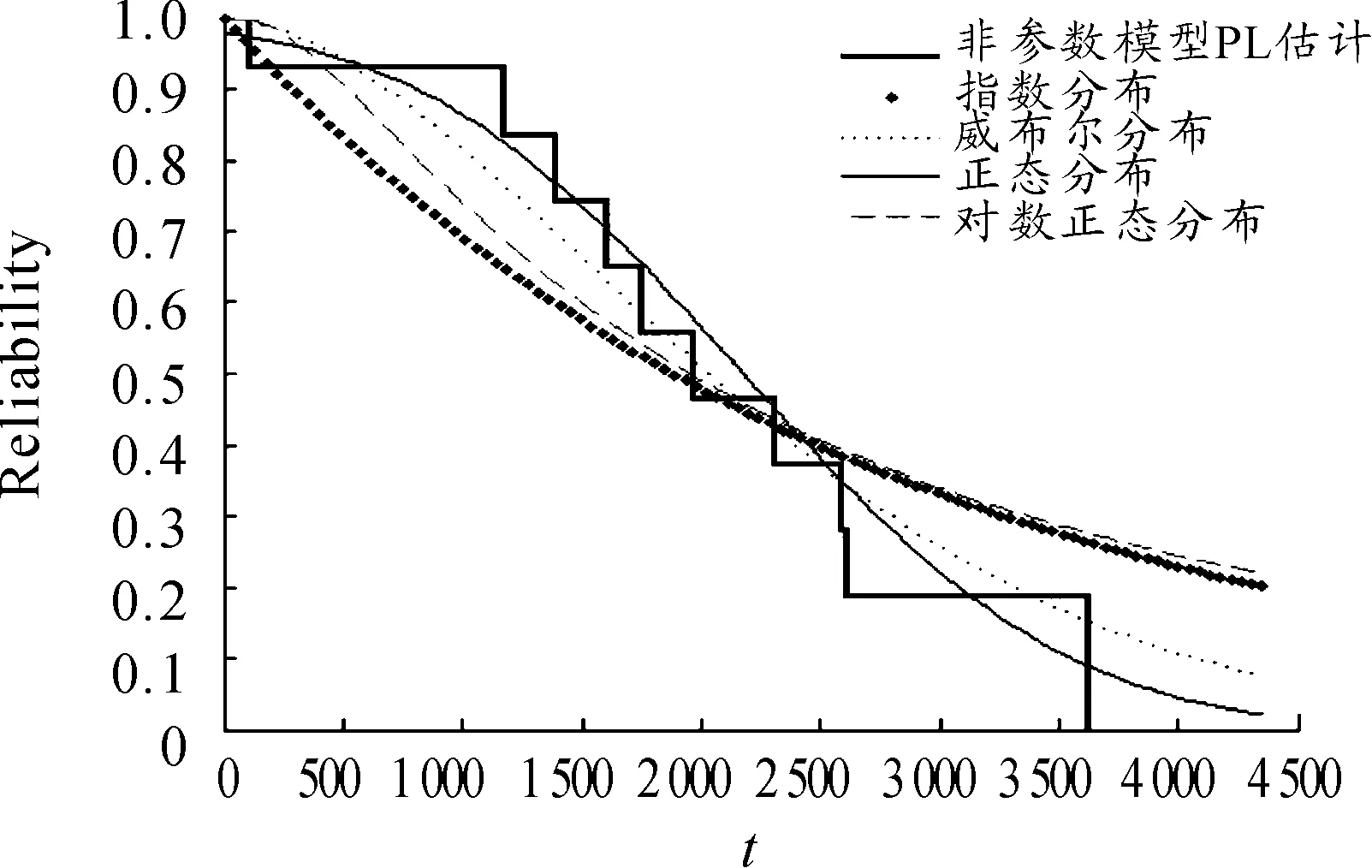
图2　右删失数据非参数估计与参数模型的比较

指数威布尔正态对数正态偏差面积1155.8340.95220.011609.1参数估计μ=2711.4a=2512.0b=1.7μ=2175.7σ=1072.5μ=7.5762σ=1.0364

5结束语

本文针对导弹右删失数据分布未知，缺少有效的参数分布选择方法的问题，以右删失数据的PL估计为基准，以常见(备选)分布下可靠度估计曲线与PL估计的拟合距离(拟合偏差)为衡量标准进行数据分布选择，并列举实例，从而为可靠性参数的描述提供了量化支持。此选择方法可以定量反映备选参数分布和右删失数据的拟合偏差，简单直观，操作方便。

参考文献：

[1]王静.导弹贮存指标体系研究[J].强度与环境，2012,39(2)：58-60.

[2]武文军，刘军，唐兴诚．防空兵部队战术[M]．北京：军事科学出版社，2001.

[3]耿飞，刘雨时．一种基于维修策略的导弹贮存可靠性模型研究[J]．装备制造技术,2009(10)：44-45.

[4]李长福，夏建中，黄跃得，等.考虑删失数据时弹药贮存可靠性评估方法研究[J].兵工学报，1996，17(4)：303-307.

[5]何书元.生存分析中乘积限估计的大样本性质[J].数学进展，1998，27(6)：481-500.

[6]梁薇．右删失数据与经验似然方法[D]．北京：北京大学,2011.

[7]姜英秀.Turnbull估计的计算方法及其比较[D].延边：延边大学，2007.

[8]TurnbullBW.NonparametricEstimationofaSurvivorshipFunctionwithDoublyCensoredData[J].JournaloftheAmericanStatisticalAssociation,1974(69)：169-173.

[9]KapalnEL,MeierP.NonparametricEstimationfromIncompleteObservations[J].JournaloftheAmericanStatisticalAssociation,1958(53):457-481.

[10]陈家鼎．生存分析与可靠性[M]．北京：北京大学出版社,2005:25-30.

[11]陈辉强，魏鑫，高飞.装备可靠性数据处理方法[J].四川兵工学报2010(07):35-37.

[12]吴翊，李永乐，胡庆军．应用数理统计[M]．长沙：国防科技大学出版社,1995：33-34.

[13]樊富友,余智超,陈明,等.制导炸弹贮存可靠性分析与探讨[J].装备环境工程,2013,10(4):102-105

(责任编辑周江川)