基于非线性能量阱的双共振峰振动抑制的力学特性研究

张也弛

（北京空间飞行器总体设计部，北京 100094）

0 引言

早在20世纪中期，Roberson 就指出：在动力吸振器中引入非线性，可以有效地增加振动抑制的带宽，使得动力吸振器的鲁棒性显著提高[1]。非线性能量阱（nonlinear energy sink,NES）是一种可实现高效振动抑制的非线性吸振器，其内部含有的强非线性立方刚度使其具有极为高效的振动能量吸收能力[2]。但同时，含有强非线性刚度也使系统的 力学特性十分复杂，尤其是强非线性系统扩充至三自由度以后，解析分析十分困难。若要对NES 的减振效果有全面认识，则力学特性的分析必不可少。自从NES 的概念提出以来，一些学者对单自由度减振对象连接一个NES 的结构力学特性进行了大量研究。文献[3]给出了非线性能量阱与线性吸振器的振动抑制效果比较，证明了非线性能量阱在振动抑制方面的优越性。文献[4-5]给出了上述 系统的内在哈密顿系统在1:1 内共振条件下的力学分析。文献[6-7]中研究了哈密顿系统周期解在主脊线上的分岔现象，并指出该哈密顿系统对非保守系统的力学特性有重要影响[8]。线性振子与NES 间的能量传递被广泛研究：文献[9-10]中通过一种新的有限相位轨迹手段深入研究能量传递过程，并使得多种能量传递机制得以揭示；文献[11]指出，内在哈密顿系统的1:1 内共振是引发能量传递的最有效机制；文献[12]在此基础上进一步指出，在1:1内共振附近的“超慢”半周期是引发最优能量传递的途径。

文献[13-16]通过解析和试验手段，在简谐载荷作用下对一个线性振子连接一个NES 的结构进行了研究。文献[13]揭示出在产生准周期振动时，NES具有较好的振动抑制效果。文献[14]在文献[13]基础上研究了系统周期解的分岔现象，给出产生准周期振动的两种机制。基于对系统非线性力学的深入研究，Starosvetsky 等人[15-17]发现：NES 产生强调制响应时，其振动抑制效果最出色，因此系统响应的稳定性问题也开始受到关注。

某些对振动敏感的有效载荷对振动环境的要求较高，在进行整星振动试验时，有时会发生局部振动环境不能满足此类有效载荷要求的情况。如果妥善应用NES 进行局部减振，则可在结构定型后较方便地解决此类问题。上述研究已证明了NES对单个共振峰具有良好的振动抑制效果，但在航天应用背景中，振动环境超标现象有时不止出现在一个单一频点附近，而是出现在一个相对单共振峰而言宽得多的频带范围内，这就要求减振装置具备一定的宽频振动抑制能力，但目前对NES 的宽频减振能力的研究是有所欠缺的。

本文研究在正弦激励作用下，NES 对减振对象的两个不同共振峰能否同时实现良好的振动抑制效果，借此分析NES 对较宽频带内的多共振峰的振动抑制能力。为达到这个目的，构造了一个受简谐激励作用的三自由度系统，包括一个两自由度线性主结构和一个连接在其末端的单自由度NES。首先提出使用增量谐波平衡法计算该系统的平衡点（周期解），之后使用Floquet 理论对周期解的稳定性进行判断。通过上述解析分析揭示了该系统内部存在的局部分岔现象，全面认识了系统的力学特性。最后通过数值计算验证了解析分析的结果。

1 系统模型

为了研究NES 的宽频振动抑制能力，首先构造如图1所示的系统（设为S），图中左侧两个方形质量块代表主结构的两个自由度，主结构具有两阶固有频率；右侧的圆形质量块代表单自由度NES。

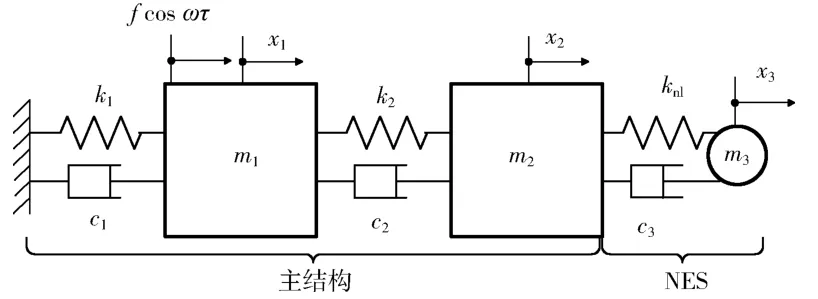
图1 耦合振子结构图 Fig.1 Schematic diagram of the coupled oscillators

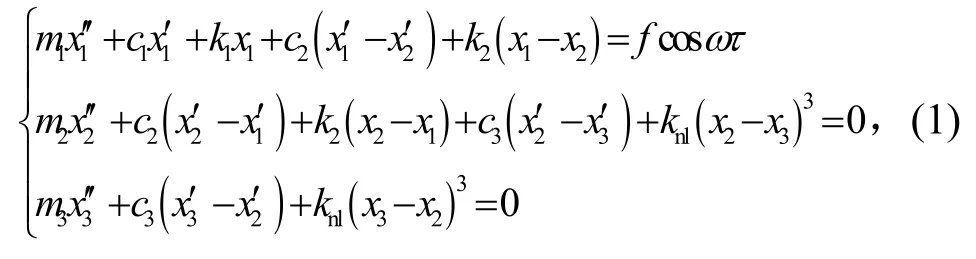
对图1结构建立如下方程：

式中：m1、m2和m3分别为三部件的质量；c1、c2和c3为线性阻尼；k1、k2为线性刚度；knl为立方刚度；f为激励力幅值；ω为激励圆频率；x1、x2和x3分别代表m1、m2和m3的位移。下面分析NES能否对m1、m2的两个不同共振峰同时实现良好的振动抑制效果。

2 系统平衡点的求解及稳定性分析

2.1 基于增量谐波平衡法的平衡点求解

本文的研究中并不限定系统S 中的knl为小量，也就是说系统S 为三自由度强非线性系统。由于对NES 力学特性的研究多针对两自由度系统，解析分析困难相对较小，目前分析手段集中于复变量-平均法（complexification-averaging method,CAM）和谐波平衡法。但对三自由度甚至更高自由度的强非线性系统来说，应用这两种方法简化分析模型不仅十分烦琐，而且由于得不到简单的平衡点解析表达式，也丧失了这些方法的主要优点。

增量谐波平衡（incremental harmonic balance method,IHB）法[18]基于谐波平衡法发展而来，是一种半数值、半解析的方法，具备谐波平衡法的优点，适用于强非线性系统的分析，且求解多自由度非线性系统时，应用IHB 法推导公式更简便。因此，本文首次采用IHB 法求解含NES 的系统的周期解。在求解之前，首先应该推导系统求解方程：

对系统S 引入时间尺度

则系统S 可变换为

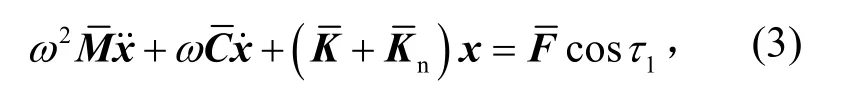
其中：

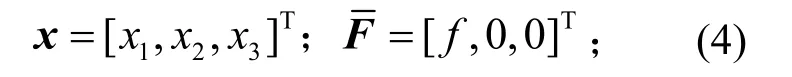
,,分别为系统的质量阵、阻尼阵和线性刚度阵，具体为

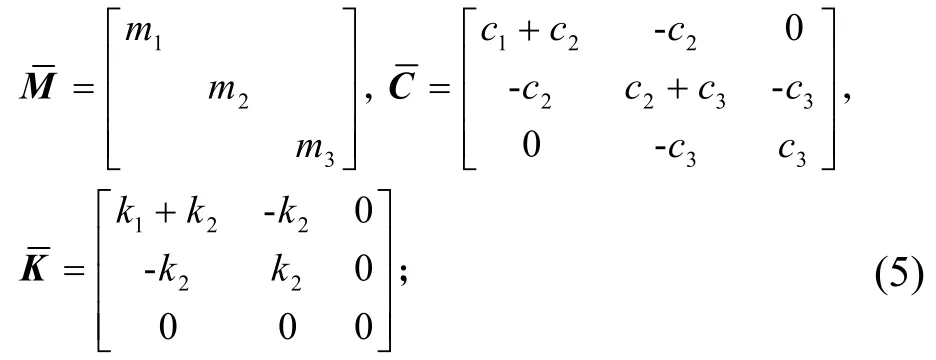
为系统的立方刚度矩阵，具体形式为

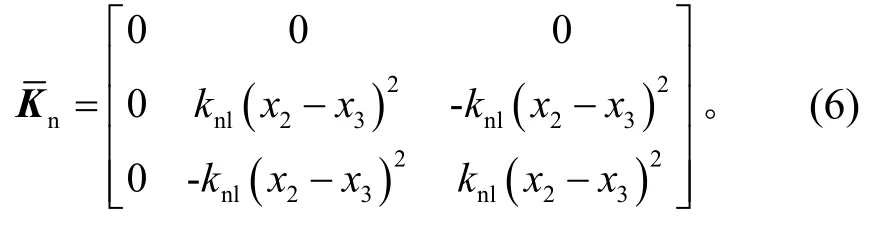
定义系统在激励力大小为F0，激励频率为ω0时的振动状态为xi0，i=1,2,3，则其临近状态可以用增量形式表示为

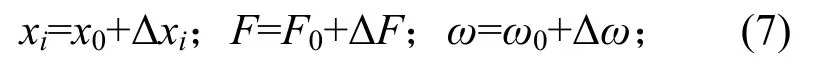
其中Δxi、ΔF和Δω表示微小增量。将式(7)代入式(3)，忽略高阶小量，可得关于Δx的线性微分方程组

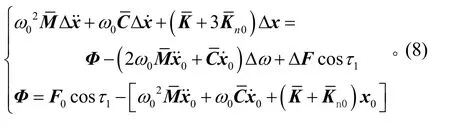
其中：

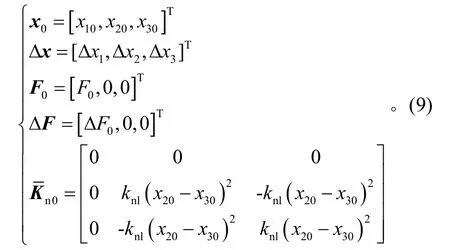
方程(3)内含有立方刚度，假设其稳态周期解为

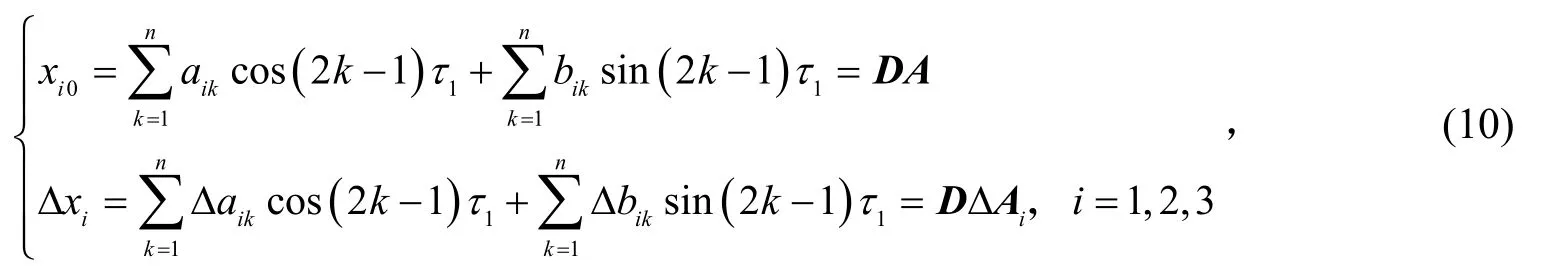
其中：

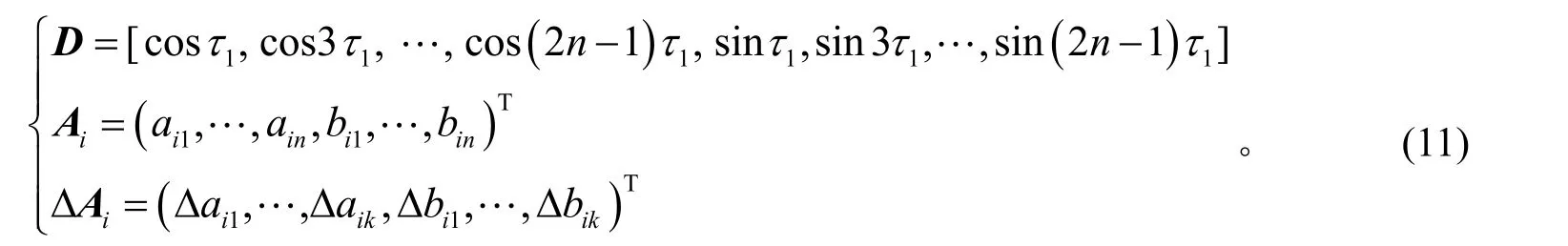
系统的稳态周期解可以表示为

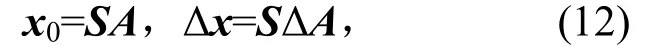
其中：

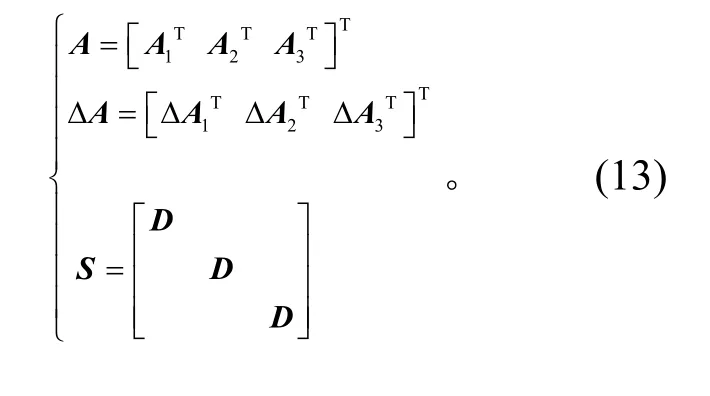
将式(12)代入式(8)，并应用伽辽金平均过程，则有

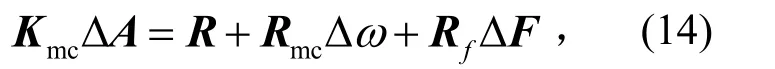
其中：

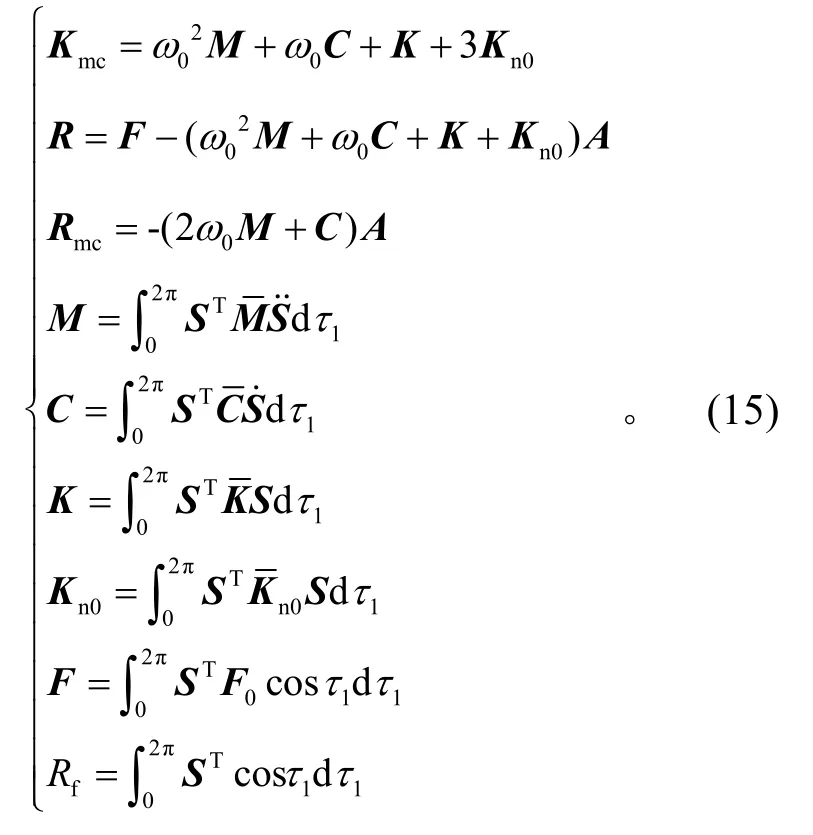
应用牛顿迭代法，可对以上方程进行求解。

2.2 平衡点的稳定性判定

2.1 节对系统S 的平衡点建立了求解方程，本节进一步判定平衡点的稳定性。

由于式(3)在其周期解附近线性化后成为线性时变周期系统，因此在后面的分析中，本文采用Floquet 理论判断周期解的稳定性，求解过程如下。

将式(3)在周期解附近线性化，得到：

其中：

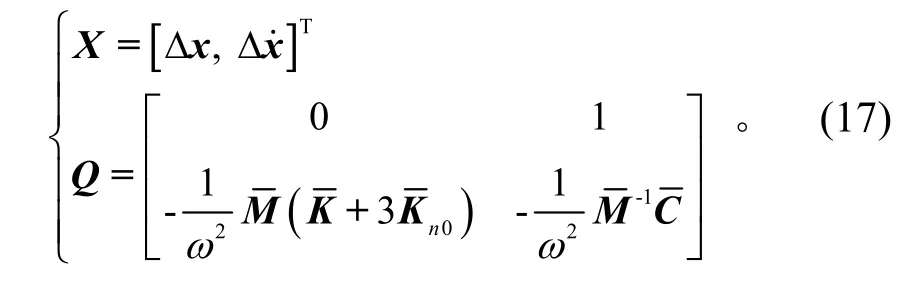
设X(τ1)为方程(16)的基础解矩阵，则由解的周期性易知X(τ1+2π)也为方程的基础解矩阵。对于这2 个基础解矩阵，一定存在非退化矩阵G，使得

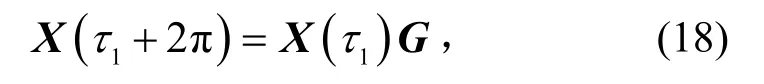
其中G称为Floquet 转移矩阵或单值矩阵。当G的所有特征值的模小于1 时，则系统的周期解渐近稳定；当G的所有特征值的模小于等于1，且模等于1 的特征值只有一次初等因子时，则系统的解稳定；当G至少有1 个模大于1 的特征值或至少有1 个模等于1 的特征值有非一次初等因子时，则系统的解不稳定。单值矩阵G的求解方法如下：

设X含有n个元素，G可采用如下积分求得

其中：y含有n2个元素；H为n2×n2的方阵，且

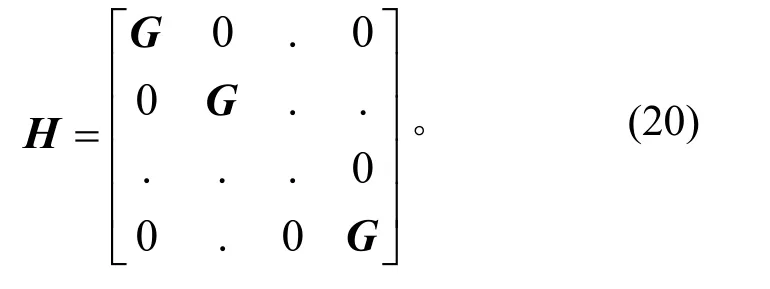
积分初值为

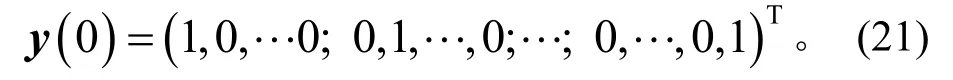
将式(21)从0 积分至2 后，则y(2π)的前n个元素即为G的第1 列，n+1 到2n个元素为G的第2 列，依次类推。

3 结果和讨论

3.1 分析结果及讨论

本节对系统S 进行求解和分析，并用数值解法对解析求解结果进行验证，所有计算在MATLAB软件环境下完成编程。系统参数取m3=0.14,k1=1.5,k2=1.2,c1=0,c2=0.005,c3=0.005,f=0.05,m1=1,m2=1.2,knl=0.2。

图2为由IHB 法计算得到的系统S 中三振子的频率和响应图，A1、A2和A3分别表示x10、x20和x30周期解的幅值，仿真忽略高次谐波，即有图2中用实线表示 经Floquet 理论判断为稳定的周期解，虚线表示不稳定周期解，用小圆圈表示四阶龙格-库塔法对稳定周期解进行的数值验证，数值分析时积分初始值均为0。由图2可见，用小圆圈表示的结果全部分布在IHB 法计算得到的稳定解分支上，即数值结果与解析结果吻合。图3为无NES 连接时两振子的幅值曲线，用来比较说明NES 的减振能力。为了最大限度地排除阻尼对振动的抑制作用，对主结构第一个质量块采取极端的无阻尼假设，即令c1=0。

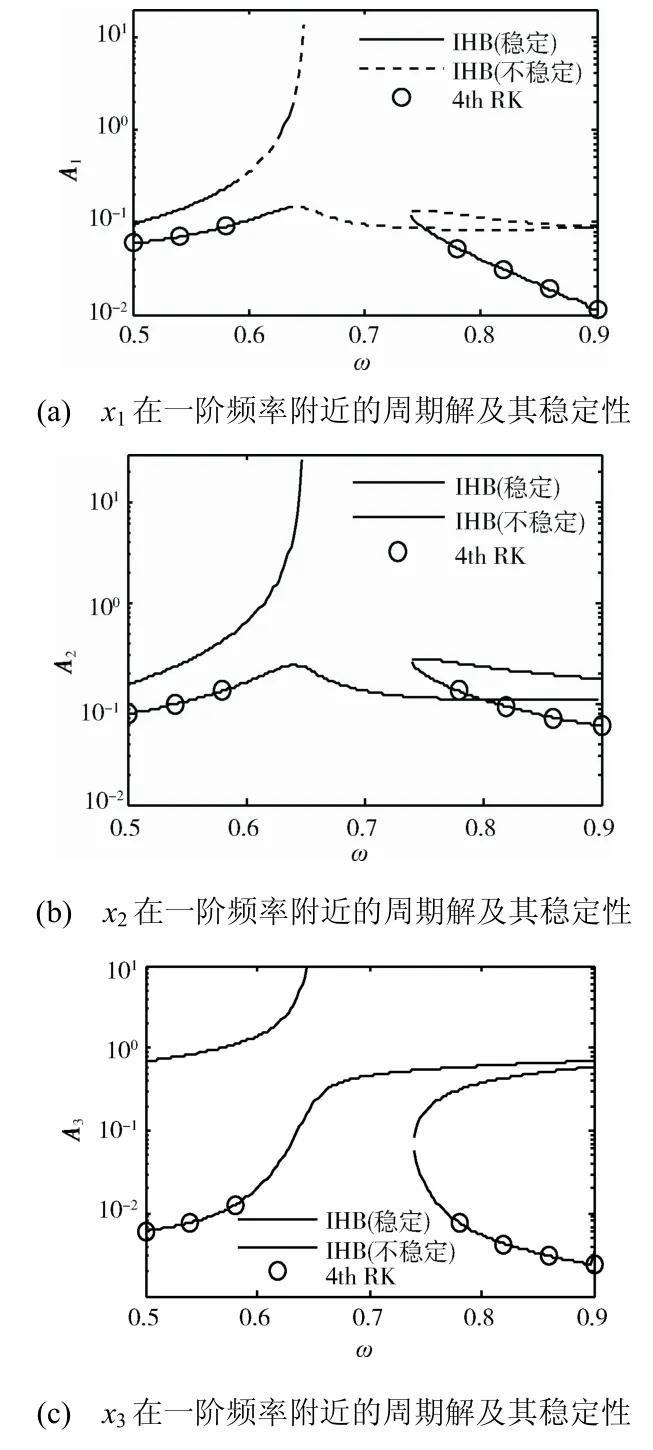
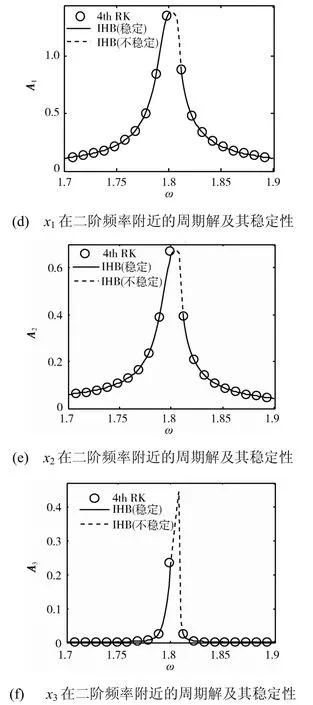
图2 三个振子的幅值-频率曲线 Fig.2 Amplitude-frequency curves of the three oscillators

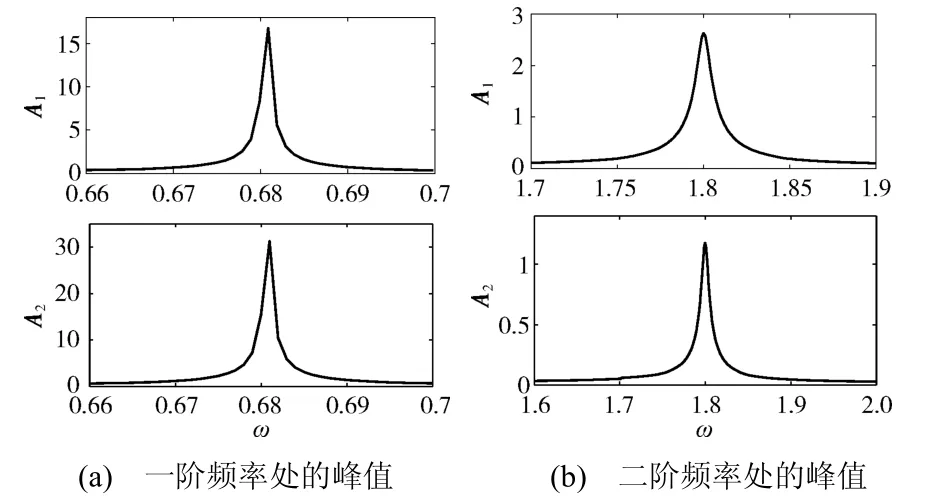
图3 无NES 时两振子的振动峰值 Fig.3 Amplitude of the two oscillators without NES

由图2(a)可见，A1在ω=0.648 时的一组周期解分支上有最大值10.5，虽然此时响应幅值较大，但与图3(a)中A1的峰值相比，该不稳定解分支的最大值也小于无NES 时的系统响应幅值（16.7），说明在该组NES 设计参数取值下，即使在最坏情况下，NES 也不会起到放大振动的作用。

另外由图2(a)～图2(c)可见，该系统存在两种局部分岔现象。其中，随ω变化，虚线与实线的交接点为Hopf 分岔点，当激励频率穿越该点时，周期解的稳定性发生改变；图中同一个ω值对应多个振动幅值的现象说明系统存在鞍结分岔，在鞍结分岔区域，由于存在2～3 个解，系统随初始状态（振子的初始位移、速度或加速度）的不同，对应的周期解的幅值、稳定性都可能发生变化，NES的振动抑制效果也会随初始状态的变化而不同。

在上述参数取值下，在ω=0.648 时，由四阶龙格-库塔法求解得到三振子的位移时程图，见图4。

图4(a)中系统各初值均设为0，此时为调制响应，响应在幅值较小的不稳定周期解附近摆动。图4(b)中积分初值为[x0,] =[1 0,0,20,0,20,0]，此时 初值取在幅值较大的周期解附近，可见系统振幅较大，响应落在上部周期解分支附近，与图3比较可见，此时对峰值的削减略超过30%，远不如图4(a)中的振动抑制效果。但由于底部周期解分支的存在，一般需要系统具有较大初始能量，响应才会跳跃至上部周期解附近，而这种强扰动在实际工程情况中出现的概率较小。因此，一般情况下，主结构 的振动幅值应在底部解分支所确定的幅值附近。同时，图4说明，在ω=0.648 时，随初始条件的不同，系统确实存在2 个不同的周期解，证实了系统内鞍结分岔的存在。这种力学特性使得仅靠数值计算难以得到系统S 的全部解，必须应用解析方法得到系统的全部解分支，才能对NES 的减振效果有全面的认识。因此应用NES 进行航天器局部振动抑制时，必须注意分岔区域的解分支分布。

3.2 与无减振装置情况的比较

经过3.1 节的分析，对系统S 的周期解及其稳定性已经有了全面的认识，解析结果说明系统内不存在振动放大现象，系统在一阶模态附近存在鞍结分岔和Hopf 分岔，在二阶模态附近的力学特性则相对简单。下面基于前面的分析结果，使用四阶龙格-库塔法计算系统在积分初值为0 时的响应，并与无附加NES 的系统进行响应能量的比较，以了解NES 的减振能力。

图5给出了上述两自由度线性主结构在无NES 连接时，在与3.1 节分析中同样激励条件下的振动响应能量曲线。图6为连接NES 后两自由度结构的振动能量图，NES 的质量为减振对象质量的14%。在ω=0.643 附近，周期解受鞍结分岔影响跳跃到了较高的解分支附近，造成了一个局部峰值；但与图5中无NES 的情况相比，NES 仍使第一个振子的2 个振动能量峰值分别降低76%和75%；第二个振子的2 个振动能量峰值分别降低了25%和94%。

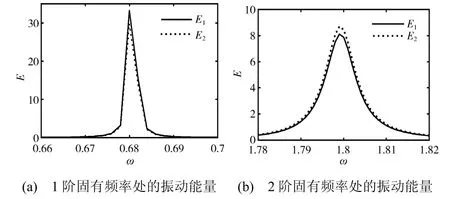
图5 两自由度结构（减振对象）在简谐激励下的 振动能量图 Fig.5 Vibration energy of the two-DOF main structure (which structure for vibration suppression)under harmonic force

另外，本文未进行NES 振动抑制效果最优化的研究，而通过调节NES 参数还可以取得更好的振动抑制效果。图7中NES 的质量为减振对象质量的22%。通过图7与图5比较可知：NES 使第一个振子的 2 个振动峰值分别降低 99.95%和68.8%；第二个振子的2 个振动峰值分别降低了99.9%和92.5%。可见，NES 可同时对2 个振子的2 个共振峰起到良好的振动抑制作用。

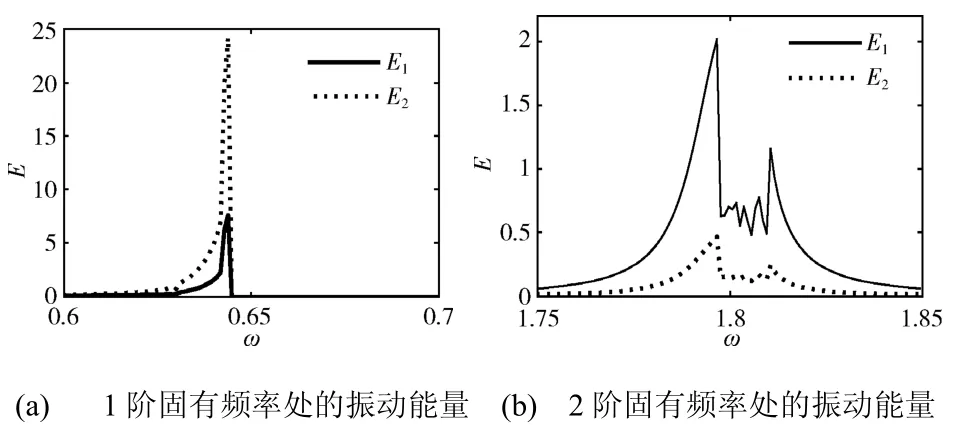
图6 连接NES 后两自由度结构的振动能量图 Fig.6 Vibration energy of the two-DOF main structure with an NES attached

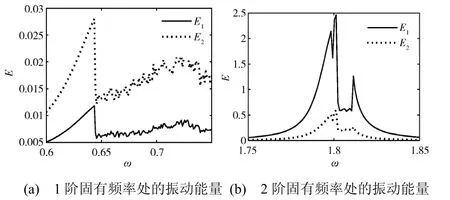
图7 连接NES 后两自由度结构的振动能量图 Fig.7 Vibration energy of the two-DOF main structure with an NES attached

需要说明的是，本文专注于揭示NES 的力学特性，并给出NES 用于减振时的一般性分析与设计方法，未针对某一特定问题。因此，仿真中所有参数均采用了无量纲量，但这并不与工程脱节，在本文研究基础上可进一步拓展至工程实际。例如：取m1=10 kg,m2=12 kg，NES 的质量m3=1.4 kg,k1=15 000 N/m,c3=0.5 N/(m/s),k2=12 000 N/m,c2=0.5 N/(m/s),f=500 N。再将时间尺度缩小100 倍（τ=100t,dx/dτ=dx/100dt）即可换算得到与图2仿真中相同的参数。相对的，图7中2 个受到抑制的振动峰值对应的圆频率分别约为68 和180 rad/s。NES 作为一种被动的振动抑制手段，具有不需要额外能源，鲁棒性、可靠性高，简单易用等特点，在航天器局部多共振峰的抑制方面具有良好的应用前景。

4 结束语

本文对非线性能量阱连接一个两自由度线性主结构的对象进行了研究，首次使用IHB 法求解了系统的周期响应，并用Floquet 理论判断了响应的稳定性。发现系统中存在分岔现象，进一步分析了该现象对NES 的设计和使用可能造成的影响，指出在NES 设计时有必要考虑分岔问题。分析结果表明，单自由度NES 具有良好的宽频振动抑制能力，使第一个振子的2 个振动峰值分别降低了99.95%和68.8%；第二个振子的2 个振动峰值分别降低了99.9%和92.5%。NES 在航天器局部振动抑制、星上敏感单机振动抑制等方面具有良好的应用前景。

（References）

[1] Roberson R.Synthesis of a nonlinear dynamic vibration absorber[J].Journal of the Franklin Institute,1952,254(5): 205-220

[2] Kopidakis G,Aubry S,Tsironis G P.Targeted energy transfer through discrete breathers in nonlinear systems[J].Physical Review Letters,2001,87: 165501

[3] Starosvetsky Y,Gendelman O.Attractors of harmonically forced linear oscillator with attached nonlinear energy sink II: optimization of a nonlinear vibration absorber[J].Nonlinear Dynamics,2008,51(1/2): 47-57

[4] Gendelman O,Manevitch L,Vakakis A,et al.Energy pumping in coupled mechanical oscillators: Part I: dynamics of the underlying Hamiltonian systems[J].Journal of Applied Mechanics,2001,68(1): 34-41

[5] Vakakis A,Gendelman O.Energy pumping in coupled mechanical oscillators: Part II: resonance capture[J].Journal of Applied Mechanics,2001,68(1): 42-48

[6] Lee Y,Kerschen G,Vakakis A,et al.Complicated dynamics of a linear oscillator with a light,essentially nonlinear attachment[J].Physica D,2005,204(1/2): 41-69

[7] Kerschen G,Lee Y,Vakakis A,et al.Irreversible passive energy transfer in coupled oscillators with essential nonlinearity[J].SIAM Journal on Applied Mathematics,2006,66(2): 648-679

[8] Quinn D D,Gendelman O,Kerschen G,et al.Efficiency of targeted energy transfers in coupled nonlinear oscillators associated with 1:1 resonance captures: Part I[J].Journal of Sound and Vibration,2008,311(3/4/5): 1228-1248

[9] Manevitch L I,Kovaleva A S,Manevitch E L,et al.Limiting phase trajectories and non-stationary resonance oscillations of the Duffing oscillator: Part 1: a non- dissipative oscillator[J].Communications in Nonlinear Science and Numerical Simulation,2011,16: 1089-1097

[10] Manevitch L I,Kovaleva A S,Manevitch E L,et al.Limiting phase trajectories and nonstationary resonance oscillations of the Duffing oscillator: Part 2: a dissipative oscillator[J].Communications in Nonlinear Science and Numerical Simulation,2011,16: 1098-1105

[11] Kerschen G,Gendelman O,Vakakis A,et al.Impulsive periodic and quasi-periodic orbits of coupled oscillators with essential stiffness nonlinearity[J].Communications in Nonlinear Science and Numerical Simulation,2008,13(5): 959-978

[12] Sapsis T P,Vakakis A,Gendelman O,et al.Efficiency of targeted energy transfers in coupled nonlinear oscillators associated with 1:1 resonance captures: Part II: analytical study[J].Journal of Sound and Vibration,2009,325(1/2): 297-320

[13] Gendelman O,Gourdon E,Lamarque C H.Quasiperiodic energy pumping in coupled oscillators under periodic forcing[J].Journal of Sound and Vibration,2006,294(4/5): 651-662

[14] Starosvetsky Y,Gendelman O.Quasi-Periodic response regimes of linear oscillator coupled to nonlinear energy sink under periodic forcing[J].Journal of Applied Mechanics,2007,74(2): 325-332

[15] Starosvetsky Y,Gendelman O.Attractors of harmonically forced linear oscillator with attached nonlinear energy sink I: description of response regimes[J].Nonlinear Dynamics,2008,51(1/2): 31-46

[16] Starosvetsky Y,Gendelman O.Response regimes of linear oscillator coupled to nonlinear energy sink with harmonic forcing and frequency detuning[J].Journal of Sound and Vibration,2008,315(3): 746-765

[17] Starosvetsky Y,Gendelman O.Bifurcations of attractors in forced system with nonlinear energy sink: the effect of mass asymmetry[J].Nonlinear Dynamics,2010,59(4): 711-731

[18] 陈树辉.强非线性振动系统的定量分析方法[M].北京: 科学出版社,2006