基于混合FE-SEA方法的航天器支架车声振响应影响分析
朱卫红,赵小宇,邹元杰
(北京空间飞行器总体设计部,北京 100094)
0 引言
声振环境是航天器在任务周期内经受的一类非常重要的力学环境[1]。声振环境频带宽(10~ 10 000 Hz),主要包括发动机的喷流噪声和气动噪声,一般通过整流罩的内声场直接作用于航天器上,可造成结构的疲劳以及关键电子设备的失效,因此航天器声振响应的预示和试验在研制过程中有着举足轻重的地位[2]。在航天器声振试验过程中需要使用地面支撑设备,这就导致了试验时的真实边界非常复杂,且在进行声振预示分析时对这些边界进行精确建模非常困难,比较典型的如星箭系统级噪声试验中的气垫车悬浮边界和航天器整星噪 声试验中的支架车固支边界等。如何在声振预示中评估和处理这类地面支撑设备对声振响应结果的影响就成为一个值得研究的课题。
目前航天器声振预示分析的主要方法包括有限元/边界元方法(FE/BEM)、统计能量分析(SEA)方法和混合有限元-统计能量分析(Hybrid FE-SEA)方法[3]。FE/BEM 方法的特点在于能够对结构和声空间进行精确建模,可获得结构不同位置的响应细节,但是随着分析频率的升高,计算效率急剧降低。统计能量分析方法的特点在于建模简单,计算效率高,然而其基本参数获取困难且只能获得子系统的平均响应,因此在工程应用中有很大的局限性。
混合FE-SEA 方法兼有上述两种方法的优点:对关心的关键结构通过有限元建模获取精确响应,对一些具有高频动力学特性且不关心响应细节的子系统建立统计能量模型,然后将两种模型通过互易关系耦合后进行求解可获得系统响应。
混合FE-SEA 方法自2005年提出以后受到了国内外学者和工程师的关注,并已广泛应用于航空航天领域。2007年,Knockaert 等[4]采用该方法对CALIPSO 卫星的声振随机响应进行了分析并取得了理想的预示结果,其中星体结构为有限元模型,而声场为统计能量模型。2008年,NASA 格林研究中心的Jeffrey[5]采用该方法对ACTS 卫星的发射天线进行了中低频声振响应分析,同时采用边界元法对预示结果进行了评估,结果表明混合FE-SEA法具有很好的预示精度,并且其分析效率高于边界元方法。在国内,邹元杰等[6]采用混合FE-SEA 方法对宽频声激励作用下的卫星结构响应进行了分析,研究了星体结构在混合激励下的响应;罗研朝等[7]运用该方法对含支架组件航天器的噪声响应进行了分析,取得了较好的预示结果;张瑾[8]开展了混合FE-SEA点连接建模理论的研究及试验验证工作。
支架车是航天器在地面研制过程中重要的地面支撑设备。本文基于混合FE-SEA 方法,研究支架车在不同模型和工况下对航天器结构声振响应的影响,研究结果可为后续航天器的声振试验、建模仿真及分析验证提供一定的参考。
1 混合FE-SEA 基本理论
基于波动理论的混合FE-SEA 方法[7]依据系统的特征尺寸与波长的相互关系,将系统划分为多个子系统,若子系统的特征尺寸大于系统波长,则用有限元建模,反之用统计能量分析方法建模,两种不同模型之间的耦合关系则通过统计能量子系统的直接场和混响场的互易关系建立[9]。
假设有限元模型的动力学刚度矩阵为Dd,统计能量模型与有限元模型连接的边界对统计能量模型的辐射矩阵(直接场动刚度矩阵)为Ddir,则整个系统的动力学刚度矩阵为

式中:N为系统中与有限元模型连接的统计能量分析模型的数目。在第m个统计能量模型的混响场中,混响场能量会在连接边界产生受挡力,则该受挡力与混响场能量之间的关系可通过互易关系表示为[10]
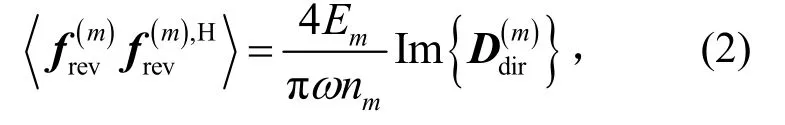
式中:Em表示第m个随机子系统在混响场中的所有能量;nm表示第m个随机子系统的模态密度;ω为圆频率。
求解得到统计能量子系统的能量后,由式(2)求得各个连接边界的受挡力,就可建立整个有限元模型的动力学方程为
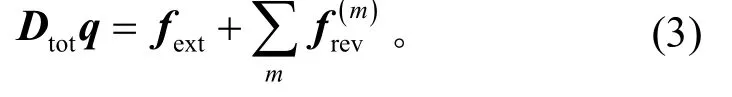
求解式(3)可得到有限元模型上任意一点的响应:
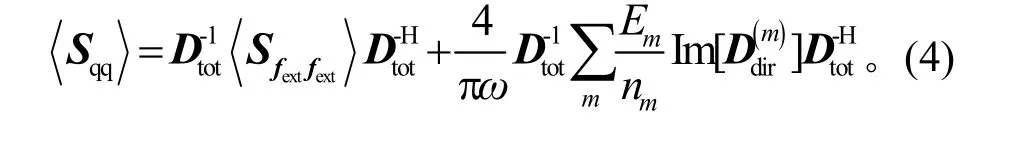
2 分析模型
某着陆器和某通信卫星共享同一台支架车,下面分别对它们进行建模。
2.1 着陆器和支架车分析模型
着陆器结构复杂,有限元建模过程中缓冲机构、氢气瓶和巡视器均等效为集中质量并与着陆器主体承力结构刚性连接。简化后的着陆器有限元模型如图1所示。

图1 着陆器有限元模型 Fig.1 Finite element model of the landing vehicle
支架车主要包括对接环、支撑和基座3 部分。为了避让发动机精测镜光路,对接环与底部基座具有15°的安装角度。支架车结构弹性模量为200 GPa,泊松比为0.3,密度为7800 kg/m3,损耗因子为1%。基座支撑最下端为4 个橡胶垫,其弹性模量为 2.3 GPa,泊松比为0.4,密度为1100 kg/m3。支架 车及其与着陆器组装后(以下简称“组装结构”)的有限元模型如图2所示。
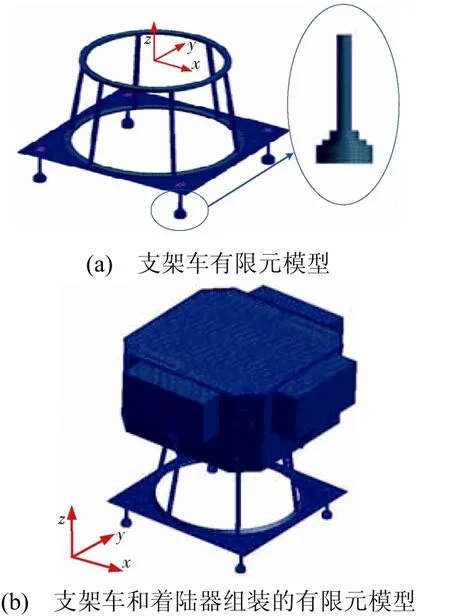
图2 支架车及其与着陆器组装结构的有限元模型 Fig.2 Finite element model of the bracket vehicle and its assembled structure with the landing vehicle
为了研究着陆器结构上各个节点响应的信息,着陆器和支架车均采用有限元进行精确建模,外部声场和内声场则用统计能量模型描述,然后两者通过混合连接建立耦合关系。为了便于对比分析,着陆器和组装结构的声压测点与结构响应测点位置完全相同,图3为结构上6 个加速度测点的位置。
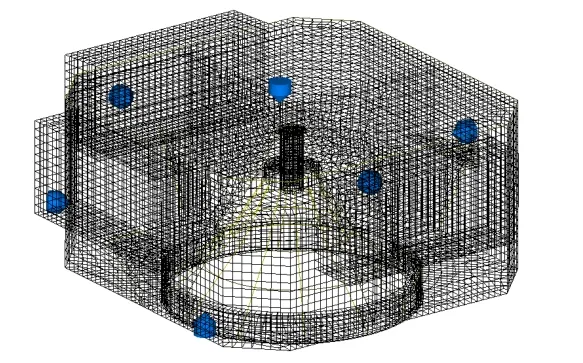
图3 着陆器结构测点布置 Fig.3 Positions of measuring sensors on the landing vehicle structure
2.2 某通信卫星分析模型
对某通信卫星的结构星平台进行建模。为了提高分析效率,对比较复杂的对地天线、南太阳电池板、西天线和主发动机组件均用集中质量代替,传感器分别布置于星体舱壁、对地天线安装处以及北电池板上,星体结构总重量约为4000 kg。简化后的模型节点数48 374 个,单元数48 898 个,损耗因子取1%。星体载荷舱和服务舱根据其几何特性划分为6 个统计能量声腔子系统,然后与星体有限元结构模型耦合求解,外声场声压通过混响载荷直接施加于星体结构外表面。由于该通信卫星模型星箭界面接口与着陆器相同,因此分析所采用的支架车模型也与着陆器的支架车模型相同,具体细节不再详述。
3 预示结果及分析
3.1 着陆器声振预示结果分析
考虑到模型比较复杂,分析频率上限取200 Hz。支架车的模态预示结果如下:表1为固支支架车的前10 阶模态,支架车的一阶模态较低,为6.10 Hz;支架车整体刚度较大,在200 Hz 内仅有26 个模态,部分模态如图4所示。

表1 支架车的低阶模态 Table1 The low order modes of the bracket vehicle

图4 固支支架车的部分模态 Fig.4 Partial modes of the bracket vehicle with clamped boundary
为了分析支架车对系统声振响应的影响,按边界不同建立3 种模型:模型1 为着陆器自由边界,模型2 为着陆器固支边界,模型3 为着陆器+支架车固支边界(实际试验边界)。在未安装支架车时,模型1 共有127 个模态,模型2 共有131 个模态;安装支架车并在其底部施加固支边界条件后(即模型3)共有155 个模态。3 种模型前11 阶模态如表2所示,200 Hz 内各阶模态变化如图5所示。可以看出:安装支架车后,系统的动力学响应变化较大,出现了一些低阶模态(20 Hz 以下),导致组合结构的共振频率总体下移。

表2 3 种着陆器模型的部分模态 Table2 Partial modes for three kinds of landing vehicle models

图5 着陆器模态分析结果 Fig.5 The modal analysis results of the landing vehicle
为了更详细地研究支架车在不同频率处的影响,声振分析带宽取1 Hz,混响载荷采用单位声压谱和整星噪声验收级声压谱两种声压条件进行分析,表3为1/3 倍频程下整星验收级试验条件。
3种模型部分测点加速度响应如图6~图8所示。
以测点9557 为例不难看出,在单位声压谱(白噪声平谱)载荷条件下,3 种模型的差异主要集中于低阶模态(60 Hz 以下),尤其是组合结构出现了低于着陆器基频的耦合模态,因此组合结构响应与未带支架车时相比差异较大:模型1 与模型3 在第1 阶共振峰处的响应差为49.24 dB,第2 阶共振峰处的响应差为25.71 dB;模型2 与模型3 在第1 阶共振峰处的响应差为47.02 dB,在第2 阶共振峰处的响应差为23.21 dB。同时可以看出,随着分析频率的提高,3 种模型的响应差异逐渐减小,如在第11阶模态处,模型1和模型3的响应差减小到0.159 4 dB,模型2 与模型3 的响应差减小到5.692 8 dB。这是由于支架车的安装导致了组合结构出现低于着陆器基频的低阶模态(20 Hz 以下),这些模态分布稀疏,表现为比较明显的共振行为,所以导致低频模态较多的组合结构模型响应与未带支架车的两种模型的响应差异大;但是随着频率的升高,响应主要取决于频带内多个局部模态共同作用,而这些模态主要为着陆器自身结构的模态,因此差异不大。

表3 整星验收级试验声压条件(1/3 倍频程) Table3 Acceptance test sound specification for spacecraft (1/3 octave)
在整星噪声试验验收级声压条件下,模型1 与模型3 的预示结果差别不明显,而模型2 的预示结果在60 Hz 以前有显著差异,如模型1 和模型3 在35 Hz 的响应差为0.166 dB,而模型2 和模型3 的响应差为17.603 0 dB。因此,在实际的噪声试验条件下,采用未带支架车的自由边界模型与实际模型更接近。由于试验条件为典型的梯形谱,所以低频处的响应差对整个分析频带内总方均根值预示结果的影响较小,3 种模型总方均根值偏差不大,模型1 与模型3 的偏差为0.111 8 dB,模型2 与模型3的偏差为0.002 6 dB。因此,在实际的噪声分析时采用自由边界和固支边界的航天器模型替代真实边界模型对结果的影响不大,但是自由边界模型在整个频段内与组合结构模型的响应谱更加吻合,着陆器固支边界模型在较低模态处仍然存在较大的响应差。

图6 测点9557 在不同条件下的加速度响应 Fig.6 The acceleration responses of the sensor 9557 under different conditions

图7 测点11013 在不同条件下的加速度响应 Fig.7 The acceleration responses of the sensor 11013 under different conditions

图8 测点9088 在不同条件下的加速度响应 Fig.8 The acceleration responses of the sensor 9088 under different conditions
3.2 某通信卫星的声振预示结果分析
为了进一步验证上述结论,考虑到模型1 和模型3 在谱型上更加吻合,因此本节以某通信卫星为例重点分析航天器结构在自由边界和组合结构固支边界下的响应。建立整星+支架车固支和整星自由边界两种模型,对比它们在单位声压谱载荷和验收级声压谱试验条件下的响应。模态分析表明,在200 Hz 内,自由边界下整星的模态数为384 个,而组合结构模态数为412 个。表4为两种模型的部分模态,可以看出组合结构的模态频率下移,出现了低于单星基频的耦合模态(低于20 Hz)。
图9~图11分别为对地天线安装处x方向、星体y方向和北电池板z方向在不同载荷条件下的加速度响应对比。从结果可以看出,不论x、y、z方向,支架车对组合结构噪声响应的影响主要集中于低阶模态(20 Hz 以下),如前3 阶共振峰处两者响应差均在12 dB 以上。这是由于在这些模态处结构表现为低频共振行为,而两种模型在该频段处模态分布差异大。但是随着频率升高,这种差异减小,而在单位声压谱下表现得非常明显;在40 Hz 以上,差异影响逐渐消失。考虑到实际噪声试验条件的特征,两种模型在整星验收级声压谱条件下的响应在整个频段差异不大,在25 Hz 以后2 种模型的响应比较接近,就总方均根而言,对地天线安装处2 种模型的偏差为0.248 8 dB,星体处为0.413 2 dB,北电池板处为0.070 8 dB。以上结论与着陆器的分析结论相同。

表4 某通信卫星的部分模态结果 Table4 Partial modes for a communication satellite

图9 不同条件下对地天线安装处x 向加速度响应 Fig.9 Acceleration responses of Earth antenna installation position in x direction under different conditions

图10 不同条件下星体y 向加速度响应 Fig.10 Acceleration responses of the satellite body in y direction under different conditions

图11 不同条件下北电池板z 向加速度响应 Fig.11 Acceleration responses of north solar panel in z direction under different conditions
4 结论
本文应用混合FE-SEA 方法建立了着陆器+支架车和某通信卫星+支架车的组合结构模型,研究了支架车对航天器声振响应的影响,主要结论如下:
1)支架车对组合结构的低频动力学特性影响较大,导致共振频率下移,同时出现了多个低于单个航天器基频的低阶模态。
2)在验收级声压谱试验条件下,相对于未带支架车的固支边界模型,未带支架车的自由边界模型与组合结构模型响应较为接近,因此,航天器在混响室内的声振响应预示可以用组合结构模型或不带支架车的自由边界模型来分析。采用固支边界模型在低阶模态(如着陆器在60 Hz 以下)响应差较大,如果关心低频响应,则不宜采用该模型。
3)支架车对组合结构的声振影响主要集中于低阶模态,随着分析频率的提高影响逐渐消失,有影响的频率上限与具体卫星和支架车形式、参数有关。对于比较高的分析频段,支架车的影响很小,3 种模型均可以选用。
上述研究结论没有考虑支架车和星体结构的应力刚化效应,包含应力刚化效应的支架车声振影响需要进一步的研究。
(References)
[1] 马兴瑞,于登云,韩增尧,等.星箭力学环境分析与试验技术研究进展[J].宇航学报,2006,27(3): 323-331 Ma Xingrui,Yu Dengyun,Han Zengyao,et al.Research evolution on the satellite-rocket mechanical environment analysis &test technology[J].Journal of Astronautics,2006,27(3): 323-331
[2] 向树红.航天器力学环境试验技术[M].北京: 中国科学技术出版社,2008: 59-77
[3] 邹元杰,韩增尧,张瑾.航天器全频域力学环境预示技术研究进展[J].力学进展,2012,42(4): 445-454 Zou Yuanjie,Han Zengyao,Zhang Jin.Research progress on full-frequency predication techniques of spacecraft’s mechanical environment[J].Advances in Mechanics,2012,42(4): 445-454
[4] Knockaert R,Frikha S,Cotoni V.Simulation of a spacecraft acoustic test by hybrid FE-SEA method: application to the CALIPSO spacecraft and comparison with experimental data[C]∥Proceedings of the 1stEuropean Air and Space Conference: Century Perspectives.Berlin,2007
[5] Jeffrey M L,Cotoni V.Vibro-acoustic response of the NASA ACTS spacecraft antenna to launch acoustic excitation,NASA/TM 2008-215168[R],2008: 1-15
[6] 邹元杰,韩增尧.宽频声激励作用下的卫星结构响应分析[C]∥全国结构动力学学术研讨会论文集.南昌,2007: 254-261
[7] 罗研朝,王闯,张熇.基于FE-SEA 方法的航天器含支架组件噪声分析[J].航天器环境工程,2014,31(3): 262-266 Luo Yanzhao,Wang Chuang,Zhang He.Acoustic response predication for a spacecraft unit with bracket based on FE-SEA method[J].Spacecraft Environment Engineering,2014,31(3): 262-266
[8] 张瑾.FE-SEA 方法在航天器力学环境预示中的应用研究[D].北京: 中国空间技术研究院,2011
[9] Shorter P J,Langley R S.Vibro-acoustic analysis of complex systems[J].Journal of Sound and Vibration,2005,288(3): 669-699
[10] Shorter P J,Langley R S.On the reciprocity relationship between direct field radiation and diffuse reverberant loading[J].J Acoust Soc Am,2005,117(1): 85-95

