MATLAB在数字滤波器设计教学中的应用

方 焯 陈西曲 陈良艳 黄海林

（武汉轻工大学，湖北 武汉 430023）

自从1965 年库利和图基发表了快速傅里叶变换算法以来，数字信号处理这一学科蓬勃发展，逐渐成为一门涉及许多学科而广泛引用于许多领域的新兴学科。数字滤波器具有精度高、稳定性好、灵活性强、便于集成、高性能等优点[1-2]，在数字信号处理中发挥着十分重要的作用。

MATLAB 软件是美国MathWorks 公司推出的一套高性能科学计算软件，它具有强大的数值分析、矩阵运算、信号处理和图形显示的功能。信号处理工具箱中包含许多由信号处理领域的权威专家编写的函数，可以直接调用，使编程变得很简单。特别在数字滤波器的设计中，MATALB 软件能够很方便的完成数值计算以及图形的绘制。下面我们具体说明MATLAB 软件分别在IIR（Infinite Impulse Response）和FIR（Finite Impulse Response）数字滤波器设计中的应用。

1 IIR 数字滤波器的设计

IIR 数字滤波器的系统函数包含零点和单位圆内的极点，因此可以用较低的阶数设计出频率选择性较高的滤波器，所用的存储单元少，计算量小、效率高。但IIR 滤波器一般不具有线性相位。设计IIR数字滤波器的思路是先把数字技术指标转换成模拟技术指标，然后设计模拟IIR 滤波器，最后映射成一个等效的数字滤波器。

我们用冲击响应不变法和双线性变换法分别设计巴特沃斯滤波器和切比雪夫滤波器为例说明MATLAB 软件的运用方法。设计IIR数字带通滤波器，给定指标为(1)200Hz＜f＜400Hz，衰减＜2dB，(2)f＜100Hz，f＞600Hz，衰减＞20dB，(3)抽样频率fs=2kHz。

先将模拟信号经过AD 转换得到数字信号，那么所设计数字滤波器的的指标为：

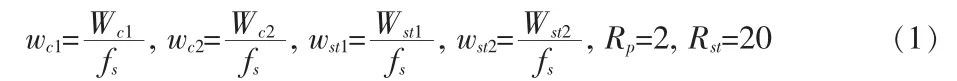
其中Wc1=200 Hz，Wc2=400 Hz 为两个通带截止频率；Wst1=100 Hz，Wst2=600 Hz 为两个阻带截止频率，fs=2000 Hz 为采样频率。wc1，wc2，wst1，wst2分别为转换得到的数字滤波器的两个通带截止频率和两个阻带截止频率。

通常的设计方法是将数字滤波器的技术指标转换成模拟滤波器的技术指标，再将模拟带通滤波器的技术指标转换成模拟低通滤波器的技术指标，然后设计模拟低通滤波器，最后将设计的模拟低通滤波器转换成数字带通滤波器。设计方法非常复杂，然而运用MATLAB 软件来设计非常方便，函数buttord 和cheb1ord 直接根据给定的技术指标返回巴特沃斯滤波器和切比雪夫滤波器的阶数和3dB 的截止频率，再用butter 和cheb1ord 函数返回所设计滤波器的系统函数。用冲击响应不变法设计，先设计出模拟滤波器，再用impinvar 函数将模拟滤波器转换为数字滤波器；用双线性变换法设计可以用该函数直接设计数字滤波器。具体程序代码如下：

fs=2000;%采样频率。

Wc=[2*pi*200 2*pi*400];Wst=[2*pi*100 2*pi*600];%通带截止频率和阻带截止频率。

Rp=2;Rst=20;%通带最大衰减和阻带最小衰减。

wc=Wc/fs;wst=Wst/fs;%所设计的数字滤波器的截止频率。

[N，Wn]=buttord(Wc，Wst，Rp，Rst，'s');%用巴特沃斯滤波器设计，冲击响应不变法，'s' 表示设计模拟滤波器，N 为阶数，Wn 为3dB 的截止频率。

[B，A]=butter(N，Wn，'s');%返回模拟滤波器的系统函数，B 为分子多项式系数，A 为分母多项式系数。

随着烟草行业信息化建设的飞速发展，卷烟工厂基本完成了基础设施建设和各类业务系统建设，这些信息系统之间相对独立，缺乏有机联系，形成了信息孤岛;各业务系统侧重于业务处理，不能进行充分的数据价值挖掘，缺乏为企业领导的综合分析、宏观决策提供有力支持。因此，建设卷烟工厂的数据中心就显得尤为迫切和重要。

[b，a]=impinvar(B，A，fs);%函数impinvar 用冲激响应不变法将模拟滤波器转化为数字滤波器，返回b 和a 分别为数字滤波器的分子和分母多项式系数。

[h1，w1]=freqz(b，a，100);%函数freqz 算出冲激响应不变法设计巴特沃斯数字滤波器的频率响应。

[N，Wn]=buttord(wc/pi，wst/pi，Rp，Rst);%用巴特沃斯滤波器直接设计数字滤波器，得到滤波器的阶数和3dB 截止频率。

[b，a]=butter(N，Wn);%返回数字滤波器的系数。

[h2，w2]=freqz(b，a，100);%函数freqz 算出双线性变换法设计巴特沃斯数字滤波器的频率响应。

[N，Wn]=cheb1ord(Wc，Wst，Rp，Rst，'s');%用切比雪夫滤波器设计模拟滤波器，得到滤波器的阶数和3dB 截止频率。

[B，A]=cheby1(N，Rp，Wn，'s');%得到模拟滤波器的系统函数。

[b，a]=impinvar(B，A，fs);%函数impinvar 用冲激响应不变法将模拟滤波器转化为数字滤波器

[h3，w3]=freqz(b，a，100);%函数freqz 算出冲击响应不变法设计切比雪夫数字滤波器的频率响应。

[N，Wn]=cheb1ord(wc/pi，wst/pi，Rp，Rst);%用切比雪夫滤波器直接设计数字滤波器，得到滤波器的阶数和3dB 截止频率。

[b，a]=cheby1(N，Rp，Wn);%返回数字滤波器的系数。

[h4，w4]=freqz(b，a，100);%函数freqz 算出双线性变换法设计切比雪夫数字滤波器的频率响应。

x=[wc/pi，wst/pi];

y=[-Rp，-Rp，-Rst，-Rst];%技术指标

plot(w1/pi，20*log10(abs(h1))，'+'，w2/pi，20*log10(abs(h2))，'^'，w3/pi，20*log10(abs(h3))，'v'，w4/pi，20*log10(abs(h4))，'o'，x，y，'*');%画图

grid;xlabel('w/pi');ylabel('20Log(|H|)');axis([0，1，-50，10]);

legend(' 巴特沃斯，冲击响应不变法'，' 巴特沃斯，双线性变换法'，' 切比雪夫，冲击响应不变法'，' 切比雪夫，双线性变换法');

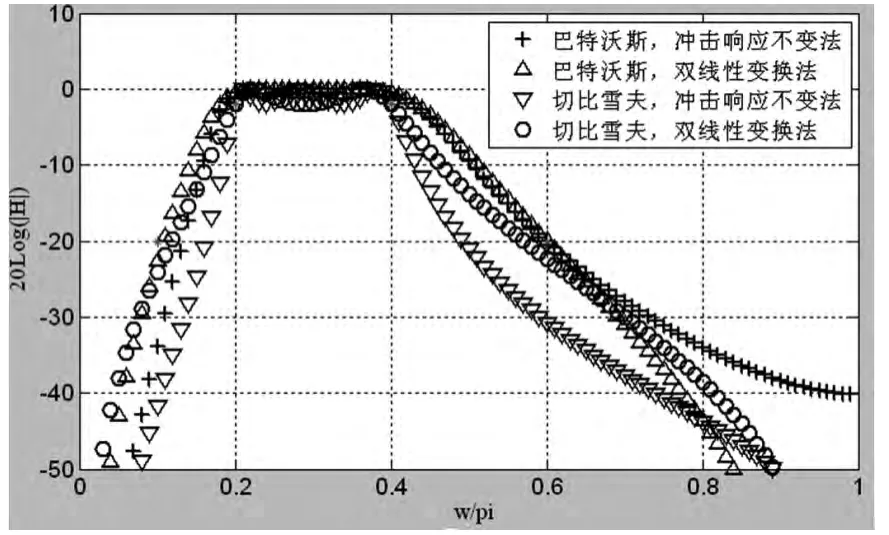
图1 IIR 滤波器的幅频响应曲线

图1 为程序运行后的滤波器的幅频响应曲线。可以看出所设计的4 种数字滤波器通带截止频率为0.2π 和0.4π，w＜0.1π 和w＞0.6π 为阻带，阻带的衰减均大于20dB，满足了数字滤波器设计的技术要求。巴特沃斯滤波器在通带没有出现波纹，而切贝雪夫滤波器在通带出现波纹；双线性变换法实现模拟滤波器到数字滤波器的映射不出现混叠现象，而冲击响应不变法实现该转换高频部分有混叠现象，因此，在高频阻带，冲击响应不变法设计的滤波器的幅频响应曲线会往上翘，所设计的滤波器的特征都符合要求。

2 FIR 数字滤波器的设计

FIR 滤波器的系统函数没有极点，保证了FIR 滤波器是稳定的。FIR 滤波器很容易具有线性相位。设计FIR 滤波器通常有窗函数法和频率采样法。

窗函数法设计FIR 滤波器的基本原理就是在时域逼近理想滤波器的单位冲击响应[3]，从而使所得到的频率响应与所要求的理想频率响应尽可能接近。这种时域逼近时通过在时域加窗的方法得到的，通过给定的技术指标选择窗函数的类型和长度。例如利用窗函数法设计一个线性相位低通FIR 数字滤波器，通带截止频率wp=0.4π，阻带截止频率wst=0.6π，阻带最小衰减50dB。常用的窗函数有矩形窗、三角窗、汉宁窗、海明窗、布莱克曼窗和凯泽窗，每个窗函数加窗后的滤波器的阻带最小衰减不一样，根据阻带最小衰减50dB 我们选择海明窗，然后根据海明窗过渡带的宽度为6.6π/N，结合需要设计的过渡带宽度wst-wp=0.2π 计算出海明窗的长度N。截止频率取通带截止频率和阻带截止频率中心，通过fir1 函数得到FIR 滤波器的系统函数，程序代码如下：

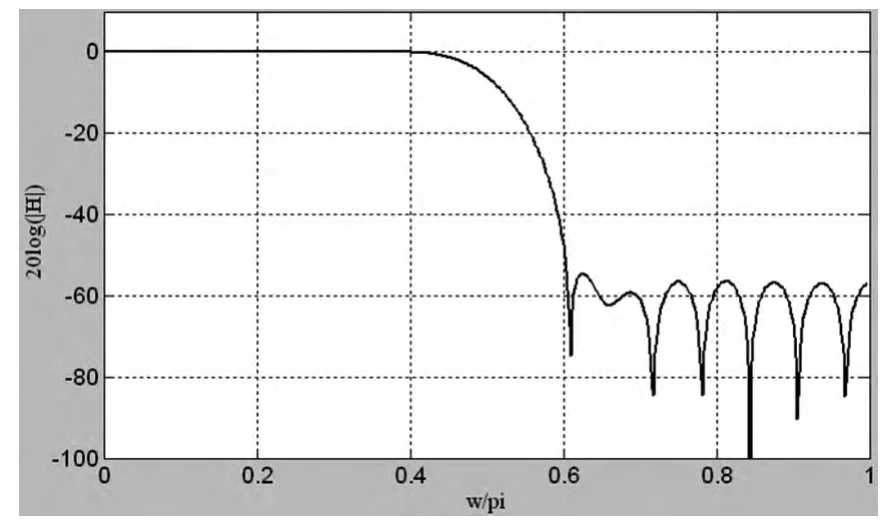
图2 窗函数法设计FIR 数字滤波器的幅频响应曲线

程序运行后，结果如图2 所示。滤波器的长度N=33，阻带截止频率0.6π 的衰减为50dB，达到了滤波器的设计指标。

频率采样法对期望的频率响应在0～2π 之间等间隔地采样，通过采样点的值还原出系统的频率响应。虽然频率采样点与理想的频率响应精确的符合，但是无法控制采样点之间如何插值。抽样点之间的理想频率特性变化越陡峭，则内插值与理想值之间的误差就越大。在过渡带两边会产生肩峰，通带和阻带也会产生波纹。这可以通过增加过渡带抽样点进行优化，例如设计一个低通FIR 数字滤波器，wc=0.5π，抽样点数为N=33，要求滤波器具有线性相位。(1)增加一点过渡带进行优化，过渡带抽样点值为0.5；(2)增加抽样点数至N=65，加两点过渡带优化，过渡带抽样点值为0.5886，0.1065。程序代码如下：

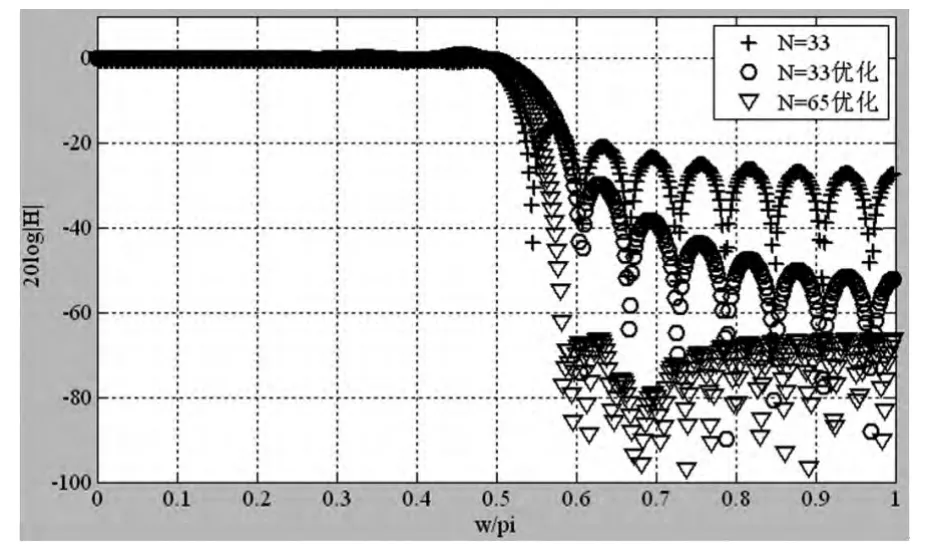
图3 频率采样法设计FIR 数字滤波器的幅频响应曲线

程序运行后，结果如图3 所示。可以看出，增加一点过渡带抽样后，过渡带的宽度由原来的2π/33，增大为4π/33，阻带最小衰减由-17dB 增大为-30dB。可见增加过渡带抽样点，阻带衰减增大，但过渡带变宽了。抽样点数增大到65 后，阻带衰减增大为-65dB，过渡带的宽度约为6π/65。若要阻带衰减增大，又不影响过渡带的宽度，就要增加抽样点数。但增加抽样点数，所设计的滤波器的延时器的数量也增大了，所以需要结合具体的应用及硬件条件选择合适的抽样点数。

3 结论

本文介绍了MATLAB 在IIR 和FIR 数字滤波器设计中的应用。可以看出MATLAB 的引入为数字滤波器的设计提供了便捷的数值计算方法，从大量的数据推导和计算中解放出来，使得数字滤波器的设计简单化、实用化，充分体现了MATLAB 软件在数字滤波器设计中的优越性。

［1］周砚江，顾焕峰，冯佳良.基于SPI 的快速多通道数据采集和数字滤波方法及应用研究[J].电子测量与仪器学报，2008，22(3)：100-104.

［2］高明，张清，赵文才.一种基于DSP 技术的平视显示器视差自动检测方法[J].国外电子测量技术，2010，29(12)：24-27.

［3］陈后金，薛健，胡健.数字信号处理[M].北京：高等教育出版社，2007.