芯块-包壳间隙对燃料棒温度场影响的数值模拟

青 涛 尹春雨 周 毅 武铃珺 辛 勇 郭兴坤

（中国核动力研究设计院核反应堆系统设计技术重点实验室，四川 成都 610213）

0 引言

在反应堆高温、高压和强辐射的运行环境中，燃料棒堆内行为的预测和评价[1]是其设计研究中极为重要的内容之一。由于辐照试验研究成本高、耗时长、在线观察难度大，而且辐照后检查也需要采用较为复杂的手段[2]。因此，随着计算仿真技术的发展，采用合理的有限元模型进行燃料棒堆内行为的数值模拟已经成为辅助设计的发展趋势和重要手段[3-4]。

考虑制造工艺可行性和功能，燃料棒设计时芯块和包壳的几何尺寸需满足公差要求，该公差决定了燃料棒装配时的芯块-包壳间隙，并允许间隙在一定允许范围内变动。芯块-包壳间隙在燃料装管时以及在运行过程中补偿燃料芯块热膨胀和肿胀是必要的，而且合适的芯块-包壳间隙设计是避免堆内运行时芯块-包壳相互作用[5]（Pellet-Cladding Mechanical Interaction，PCMI）的有效基础。

燃料棒设计准则中对燃料芯块的中心温度进行限制以保证包壳的完整性[6]。芯块-包壳间隙和燃料棒线功率是影响燃料棒温度场的重要因素。本文采用Simulation 软件对不同芯块-包壳间隙状态下的燃料棒温度场进行了数值模拟，将芯块-包壳间隙的差异对燃料棒温度场的影响进行了对比研究。

1 有限元模型

1.1 几何模型

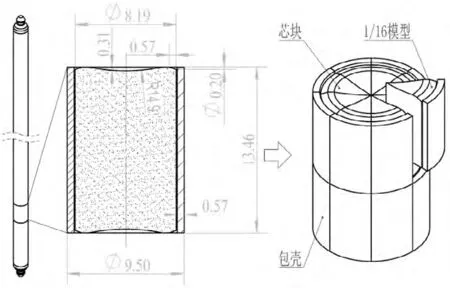
图1 燃料棒几何模型Fig.1 Geometor Model of Fuel Rod

针对燃料棒结构特征的对称性，从长度等于一个芯块高度的燃料棒轴向段上取1/16 结构作为有限元模拟的几何对象，模型见图1。该几何模型中燃料棒包壳外径Φ9.50mm、壁厚0.57mm，芯块直径Φ8.19mm、高度13.46mm，芯块两端设有0.57mm×0.20mm 的倒角和深0.31mm×R14.9mm 的碟形以避免“竹节”效应[7]（Bambooing Effect）带来的燃料芯块和包壳间的应力集中，芯块和包壳之间填充2.0MPa 的氦气。由于燃料棒周向对称性和轴向延续性，取该几何模型能对燃料棒的温度场进行有效模拟。

1.2 基本假设和边界条件

对于芯块、包壳和两者间气体的热学作用做如下假设：

（1）反应堆处于稳态工况，燃料棒的温度场不随时间变化。

（2）仅考虑填充芯块、氦气和包壳之间的热传导，不考虑热辐射效应。

（3）仅在包壳表面与冷却剂换热，忽略燃料棒的轴向传热。

（4）燃料棒包壳外侧冷却剂为稳定流动，并将堆芯释热全部带走。

燃料棒芯块均匀发热，包壳表面与冷却剂接触，热边界条件设置为：

（1）燃料棒线功率186W/cm。

（2）冷却剂温度310℃。

（3）包壳与冷却剂换热系数为20000W/m2.K。

1.3 材料的物性参数

（1）芯块热导率[8]

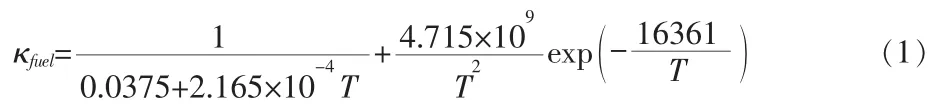
（2）包壳热导率[9]

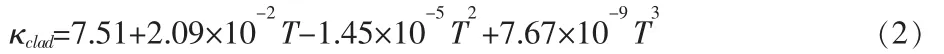
（3）氦气热导率[10]

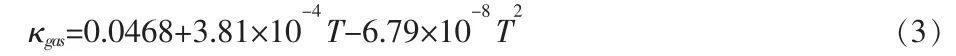
以上各式中：T 为温度，K；κfuel、κclad、κgas分别为芯块、包壳、氦气的热导率，W/m.K。

2 算法的验证

2.1 算法有效性验证

燃料棒核裂变热量的导出需依次经过芯块内的导热、芯块表面到包壳内壁的氦气导热、包壳内壁到包壳外壁的导热、包壳外壁和冷却剂的对流换热，最终由冷却剂流动将热量带出堆芯。下文通过传热学的理论公式计算来验证Simulation 对燃料棒温度场进行数值模拟的有效性。

芯块内的导热实际上是一个具有内热源的固体热传导问题。根据傅立定律[11]推导出半径r 处的芯块温度为：

芯块表面到包壳内壁的氦气导热、包壳内壁到包壳外壁的导热均可看作为一个无内热源环形薄壁层的导热问题。同样可推导出内外壁面的温降为：

包壳外壁和冷却剂的对流换热过程中所传递的热量可牛顿冷却定律[11]计算，并求得：

以上各式中：qv为芯块体积释热率，W/m3；ql为燃料棒线功率，W/m；T(r)为半径r 处的芯块温度，℃；T0为芯块中心温度（r=0），℃；κfuel为芯块热导率，W/m.K；Tn为环形薄壁层内壁温度，℃；Tw为环形薄壁层外壁温度，℃；κ 为薄壁层材料的热导率，W/m.K；Tc包壳外壁温度，℃；Tf为冷却剂平均温度，℃；lfuel为芯块高度，m；h 为包壳与冷却剂换热系数，W/m2.K。

芯块体积释热率qv和燃料棒线功率ql满足如下关系：

式中，Vfuel为芯块体积，m3。

由于材料的热导率为温度的函数，本文理论公式中采用积分热导率[12]计算。根据芯块表面温度等于氦气薄壁层内壁温度、氦气薄壁层外壁温度等于包壳内壁温度，以及公式（4）（5）（6）可分别求得芯块中心温度、芯块表面温度、包壳内壁温度和包壳外壁温度。理论公式计算与Simulation 数值模拟的结果对比见表1。从表中可以看出，除划分较粗糙的网格1 外，两者结果的最大误差均不超过0.52%、0.49%、0.77%、0.60%，说明了数值模拟算法的有效性。另外，通过对数值模拟原理的分析可以看出，产生上述误差的根源主要在于两方面：计算过程中的舍入误差和采用积分热导率计算引起的偏差。

2.2 算法收敛性验证

根据有限元方法的基本原理[13-14]，有限单元划分越密集，求解得到的结果越接近真实情况，因此收敛性验证是进行数值模拟时必不可少的环节。考虑数值模拟时的计算规模，并使求解结果尽可能接近真实情况，本文建立如表1 所示的六种网格模型，每种模型均是在对燃料棒的窄小部分进行适当加密后按网格疏密进行合理设置，网格划分疏密由低到高的排序为：网格1＜网格2＜网格3＜网格4＜网格5＜网格6。

采用上述六种网格划分模型进行燃料棒温度场数值模拟的结果见表1，燃料棒径向温度分布情况的对比见图2。由表和图可以看出，除划分较粗糙的网格1 外，其余五种网格模型相互之间对芯块中心温度、芯块表面温度、包壳内壁温度和包壳外壁温度的计算误差不超过0.016%、0.009%、0.001%、0.016%。结果之间的一致性正好说明了上述网格模型的模拟结果已基本收敛于燃料棒温度场的真实情况。由此，权衡计算规模和结果有效性，下文将采用网格3 进行燃料棒温度场的数值模拟研究。

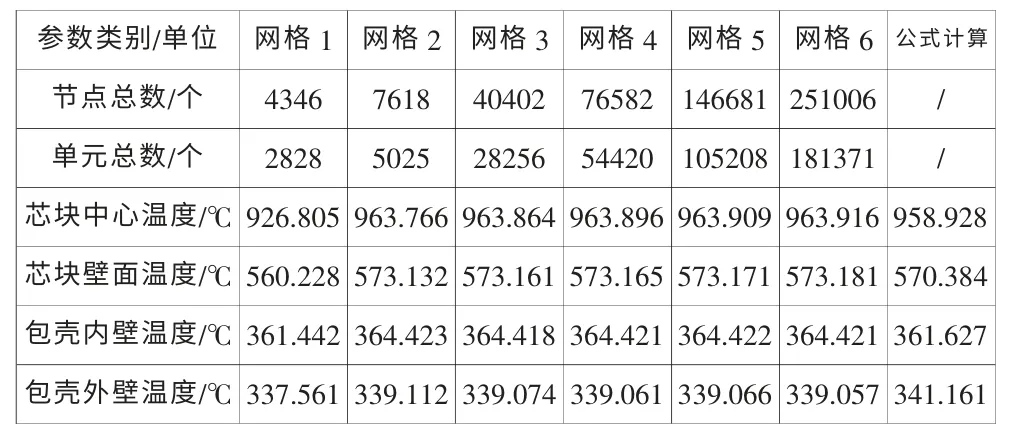
表1 算法有效性验证和收敛性验证结果Tab.1 Validity and Convergence Results of Numerical Simulation

图2 不同网格划分的燃料棒温度Fig.2 Temperature of Fuel Rod in Different Griddings

3 不同间隙状态下的燃料棒温度场

燃料棒芯块-包壳间隙是影响燃料棒温度场的重要因素之一。考虑芯块和包壳制造尺寸的差异，取包壳外径、芯块直径、芯块高度的公差分别为±0.045mm、±0.012mm、±1.27mm，芯块的倒角宽度和高度、碟形深度的公差均为±0.075mm，取模型芯块的发热量为15.647W（保持不变），分析在芯块-包壳的名义间隙、最大间隙和最小间隙状态下芯块和包壳的温度场，数值模拟结果见图3、图4、图5，不同间隙状态下燃料棒包壳和芯块尺寸的取值情况见表2。

表2 不同间隙状态的尺寸取值Tab.2 Dimensions of Different Pellet-Clad Gap States

图3 不同间隙状态下的芯块温度场Fig.3 Temperature Field Diagrams of Pelet in Different Pellet-Clad Gap States

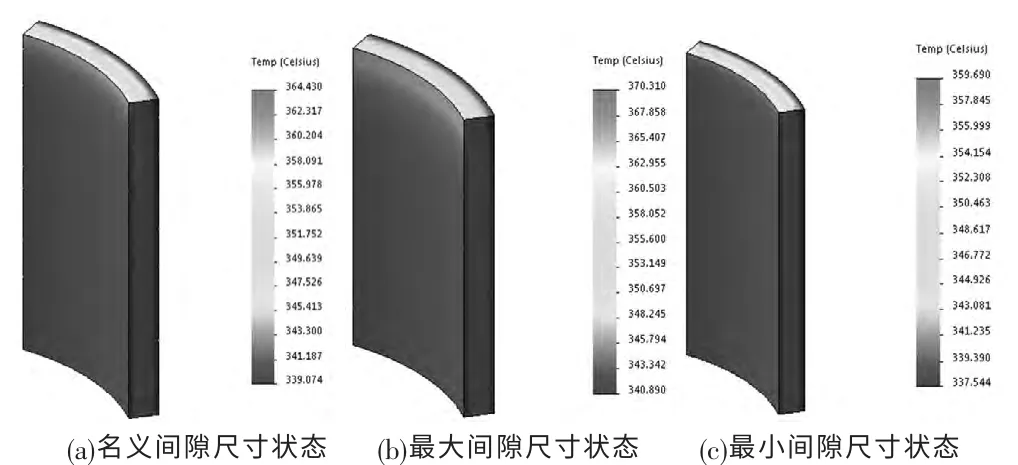
图4 不同间隙状态下的包壳温度场Fig.4 Temperature Field Diagrams of Clad in Different Pellet-Clad Gap States

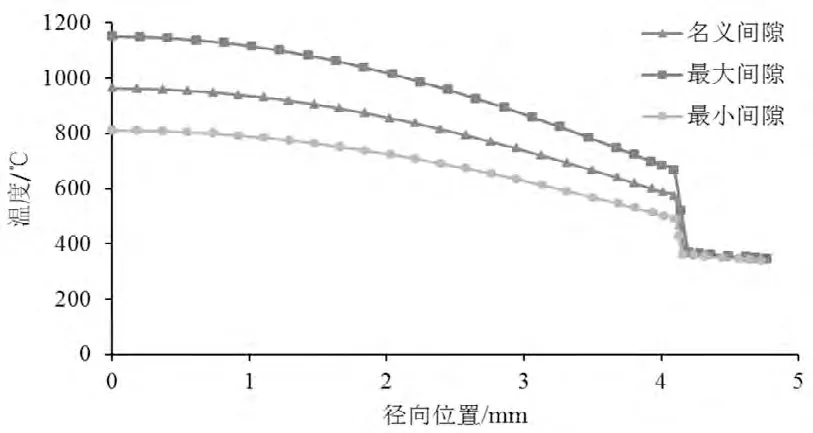
图5 不同间隙状态下的燃料棒温度场Fig.5 Temperature Field of Fuel Rod in Different Pellet-Clad Gap States

从图中可以看出：芯块-包壳间隙变化对芯块温度场的影响明显，但对包壳温度场的影响较小。与名义间隙状态相比，最大间隙状态和最小间隙状态下的芯块中心温度分别升高约188.1℃和降低约152.3℃，芯块表面温度分别升高约94.4℃和降低约83.0℃，包壳内壁温度分别升高约5.9℃和降低约4.7℃，包壳外壁温度分别升高约1.8℃和降低约1.5℃。由此可以看出，如果芯块和包壳的制造尺寸分散性较大，对包壳温度场影响不大，但芯块温度场将可能比名义尺寸下的结果偏离好几百℃，且在更高燃料棒线功率情况下产生的偏差可能更大。

4 不同功率状态下燃料棒温度场

燃料棒线功率将对燃料棒温度场产生重要影响。考虑燃料棒芯块中心温度不允许超过二氧化铀的熔点，堆芯中燃料棒线功率最大应不超过600W/cm。考虑上述名义间隙、最大间隙、最小间隙三种芯块-包壳间隙状态，对燃料棒线功率从0W/cm 到600W/cm 变化范围内的燃料棒温度场进行数值模拟，芯块中心温度的结果对比见图6。

图6 不同功率状态下燃料棒的芯块中心温度Fig.6 Temperture of Pellet in Central of Fule Rod in Different Powers

从图中可以看出，芯块中心温度随燃料棒线功率的变化近似为“S”形规律，在大约中间位置附近发生转折。对比三种不同的芯块-包壳间隙状态的芯块中心温度偏差随燃料棒线功率的变化规律可以看出，在燃料棒线功率达到约300W/cm 之前，最大间隙、最小间隙与名义间隙状态下的芯块中心温度差异几乎随线功率线性增大，且分别在约400W/cm 和350W/cm 时温度差异达到最大，之后随燃料棒线功率的增大，温度差异逐渐下降。在燃料棒线功率变化的过程中，最大间隙与名义间隙状态下的芯块中心温度最大差异达到195.9℃，最大间隙与名义间隙状态下的芯块中心温度最大差异达到166.5℃。

5 不同尺寸状态下燃料棒温度场

根据上文的分析可以看出，不同的芯块-包壳间隙状态对燃料棒温度场产生重要影响。下文将根据芯块和包壳尺寸的制造状态差异，分如下四种芯块和包壳尺寸的情况进行燃料棒温度场的数值模拟，得到芯块中心温度随芯块和包壳径向间隙变化见图6。数值模拟时取燃料棒体积释热率为0.359W/mm3（保持不变）。

（1）大包壳，即包壳尺寸按最大值，芯块尺寸由最小芯块变化到最大芯块。

（2）小包壳，即包壳尺寸按最小值，芯块尺寸由最小芯块变化到最大芯块。

（3）大芯块，即芯块尺寸按最大值，包壳尺寸由最小芯块变化到最大芯块。

（4）小芯块，即芯块尺寸按最小值，包壳尺寸由最小芯块变化到最大芯块。

芯块尺寸变化时，芯块直径、芯块高度、倒角宽度、倒角高度、碟形深度均从最小值变化到最大值；包壳尺寸变化时，包壳外径从从最小值变化到最大值并保持包壳壁厚不变。

图7 不同尺寸状态下燃料棒的芯块中心温度Fig.7 Temperture of Pellet in Central of Fule Rod in Different Dimensions

从图中可以可看出，芯块尺寸和包壳尺寸的变化对芯块中心温度的影响明显，在极限状态下，最小和最大芯块和包壳径向间隙分别为0.23mm、0.11mm，相应最小和最大的芯块中心温度分别为1044.5℃、876.0℃，温度差异达到了168.5℃。从图中还可以看出，芯块中心温度随芯块-包壳间隙变化近似成线性，通过曲线拟合得到的斜率近似为1564℃/mm。另外，与相同的芯块-包壳间隙情况下的小包壳和小芯块状态相比，大包壳和大芯块状态下的芯块中心温度略高，但最大不超过10℃。

6 结论

采用Simulation 软件进行了芯块-包壳间隙对燃料棒温度场影响的数值模拟研究。结果表明：芯块和包壳的尺寸公差造成的芯块-包壳间隙变化对芯块温度场的影响明显，但对包壳温度场的影响较小；不同芯块-包壳间隙状态下的芯块中心温度差异随线功率线性先增大后逐渐减小；芯块和包壳的不同尺寸状态下，芯块中心温度随芯块-包壳间隙变化近似成线性，与小包壳和小芯块相比大包壳和大芯块状态下的芯块中心温度略高。因此，在燃料棒温度场研究时应重点关注芯块-包壳间隙变化和功率变化对芯块温度场，尤其是对芯块中心温度造成的影响。

［1］L.V.Duyn，Evaluation of the mechanical behavior of a metal-matrix dispersion fuel for plutonium burning [D].A thesis for Master Degree，Georgia Institute of Technology，2003

［2］张平，冉木子.燃料元件辐照后破坏性检验[J].原子能科学技术，2005，7(39)：113-116.

［3］杨长江.CARR 堆芯三维流场与温场数值模拟研究[D].中国原子能科学研究院，2006，7.

［4］刘会娟.圆柱形带反射层反应堆的数值传热计算[J].核科学与工程，2010(3)：42-47.

［5］陈彭.秦山核电厂燃料棒PCMI 效应和包壳疲劳分析[J].原子能科学与技术，1998(3)：115-121.

［6］陈宝山，刘承新.轻水堆燃料元件[M].北京：化学工业出版社，2007，6.

［7］N.Marchal，C.Campos，C.Garnier.Finite element simulation of Pellet-Cladding Interaction (PCI) in nuclear fuel rods[J].Computational Materials Science，2009，45(3)：821-826.

［8］P.G.Lucuta，H.S.Matzke，I.J.Hastings，A Pragmatic Approach to Modeling Thermal Conductivity of Irradiated UO2 Fuel：Review and Recommendations [J]，Journal of Nuclear Materials，1996，232：166-180.

［9］MATPRO-09，A Handbook of Materials Properties for Use in the Analysis of Light Water Reactor Fuel Rod Behavior [J]，USNRC TREENUREG-1005，1976.

［10］C.Newman，G.Hansen，D.Gaston.Three dimensional coupled simulation of thermomechanics，heat，and oxygen diffusion in UO2 nuclear fuel rods [J].Journal of Nuclear Materials 2009，392：6-15.

［11］杨世铭，陶文铨.传热学[M].北京：高等教育出版社，2003，12.

［12］邬国伟，核反应堆工程设计[M].北京：原子能出版社，1997，12.

［13］张昭，蔡志勤.有限元方法与应用[M].大连：大连理工大学出版社，2011，8.

［14］王勖成.有限单元法[M].北京：清华大学出版社，2003，7.