最小二乘支持向量机在洪水预报中的应用

丁海蛟，车文刚 (昆明理工大学信息工程与自动化学院，云南昆明650500)

目前在全世界范围内，洪水是最具毁灭性的自然灾害之一，严重影响了正常的农业生产。为了保障正常的农业生产，防洪是非常必要的。所谓防洪，就是指根据具体的灾情特点以及水文事件演进的变化规律，研究并且采用相关的方法和对策，通过预防来减轻洪水灾害所造成的损失。防洪的主要措施有工程措施和非工程措施。工程措施造价高，而且实施的周期长，所以洪水预报作为一项重要的防洪非工程措施，它在预防洪水和防洪预案的制定中有着非常重要的作用。作为洪水预报研究对象之一的河道洪水预报可以分为水位预报和流量预报2种。笔者以河道的水位预报为研究对象，提出了基于最小二乘支持向量机(LS－SVM)的洪水预报方法。

1 洪水预报研究概况

目前有很多洪水预报的方法，例如，法国、英国和丹麦的科学家们共同合作研制了十分具有代表性的分布式水文物理模型，也就是SHE模型［1］;雷晓云等研究了BP神经网络在河道流量预报中的应用［2］;许剑华将最小二乘滤波算法构造时变参数的动态处理模式用在汇流预报模型中的回归型差分方程模型中，并将这种方法在石桥站中进行试用，达到了预期的提高模型预报精度目的［3］。近年来神经网络在预测领域被普遍的应用，但人工神经网络的局部极小点、类型和结构的选择都十分的依赖于经验，这就在很大程度上限制了其更加广泛的应用。

与人工神经网络基于经验风险最小化原则不同，基于统计学习理论的支持向量机方法根据结构风险最小化原则，在最大程度上提高了其泛化能力，其算法的局部最优解就是全局最优解［4］。最小二乘支持向量机(LS－SVM)是支持向量机的改进形式，采用平方项作为优化指标，并且用等式约束代替标准支持向量机的不等式约束，也就是将二次规划问题(QP)转化为线性方程组的求解问题，降低了计算的复杂性、提高了求解的速度。该研究应用LS－SVM建立了单输入单输出(水位—水位)和双输入单输出(水位和流量—水位)2种河道水位预测模型，并且对这2种模型进行了对比。

2 LS－SVM算法 样本数据的个数决定了标准支持向量机算法的复杂程度，因此样本数据越大，相应的二次规划问题(QP)将变得更加的复杂，计算的速度会更慢［5］。而最小二乘支持向量机，采用了不同的优化目标函数，并且用等式约束代替了原来的不等式约束，这不仅降低了计算的复杂性，还提高了求解的速度。

设训练样本集为:{xi，yi}ni=1，其中，xi∈Rd，yi∈{+1，－1}，ф为核函数的匿名映射，则LS－SVM可以表示成如下的约束优化问题:

用Lagrange法求解上述优化问题，则可以转化为求解如下的线性方程组:

式中，H=［φ(x1)Ty1…φ(xn)Tyn］，Y=［y1，…，yn］，→1=［1，…，1］，e=［e1，…，en］，α =［α1，…，αn］，消去 ω、e，得到下式:

式(3)中，Ω =HHT。设 K(xk，xl)= φ(xk)Tφ(xl)，满足Mercer条件，就是核函数，则:

所求的LS－SVM的输出是:

核函数的类型较多，比较常用的有4种［6］，该研究选取最常用的核函数，即RBF核函数:K(xi，x)=exp{－|x－xi|2/2σ2}。其中，正则化参数γ和核宽度σ是LS－SVM必须要进行调整的2个参数，因为正则化参数γ和核宽度σ是作为一个整体使用，所以γ和σ的取值将直接决定了LS－SVM的训练和泛化的能力。

3 LS－SVM预测实验

该研究建立了2个预测模型——单输入单输出(水位—水位)预测模型和双输入单输出(水位和流量—水位)预测模型，如图1所示。

为了验证LS－SVM预测方法的可行性以及有效性，以四川省自贡市某水文站2008年7月～2014年7月(即分别取每年7月份汛期)每天平均的水位数据和流量数据作为LS－SVM模型的样本数据。其中2008年7月～2013年7月的数据作为模型学习和训练的数据，2014年7月的数据作为验证数据。

3.1 样本数据预处理 将样本数据集的所有数据进行归一化处理，这样做的目的是:①避免一些特征值的范围过小，而另一些特征值的范围过大;②避免在进行训练的时候，为了计算核函数而计算内积的时候而引起数值计算困难，可能会影响建模的效果和计算的速度。因此就要将样本数据重新缩放到一个适当的范围内，该研究将样本数据缩放到［0，1］的范围内。归一化公式如下:

在训练结束时，再对数据进行反归一化，这样做的目的是:可以直观地看到预测数据的实际值而并非在［0，1］这个范围内的数值。

3.2 预测结果的评定标准 为了验证预测模型的可行性和有效性，在这里先给出预测结果的评定标准。该研究所采用的精度评定标准来自于中华人民共和国水利部《水文情报预报规范》(SL250－2000)［7］。这里给出一些比较重要的参数取值范围:

(1)结合现场的实际情况和《水文情报预报规范》的有关规定，设置水位许可误差为0.2 m。

(2)合格率。计算公式为:

式中，n是合格预报次数;m是预报总次数。其中:QR≥85.0%时，为甲级精度;70.0%≤QR ＜85.0%时，为乙级精度;60.0%≤QR ＜70.0%时，为丙级精度。

(3)确定性系数

式中，y0(i)为实测值;yc(i)为预报值;y0为实测值均值;n为资料序列长度。其中:DC≥0.90时，为甲级精度;0.70≤DC＜0.90 时，为乙级精度;0.50≤DC ＜0.70 时，为丙级精度。

(4)绝对误差

相对误差

式中，y0(i)为实测值;yc(i)为预报值。

(5)作业预报精度GI为预报误差和许可误差之比。GI≤25.0%，为优秀;25.0% ＜ GI≤50.0%，为良好;50.0% ＜ GI≤100.0%，为合格;GI＞100.0%，为不合格。

(6)经过精度评定，洪水预报方案的精度达到甲、乙2个等级者，可以用于发布正式的预报;方案精度达到丙级者，可以用于参考性预报;丙级以下者，只能用于参考性估报。

3.3 单输入单输出水位预测模型(水位—水位) 首先选取核函数。对于最小二乘支持向量机核函数的选择问题，目前在国际上还没有形成一个统一的选择模式，一般凭借经验来进行选择，而且一般优先考虑径向基函数(RBF核函数)，所以该研究中也选择RBF核函数。其次，确定γ和σ22个参数。根据参考文献［8］，采用网格搜索法寻找最优参数，最终确定 γ=295.6，σ2=301.2。利用2008年7月 ～2013年7月的数据对模型进行训练后，对2014年7月测试集的数据进行预测，预测结果见图2。

对模型的输出进行分析，结果见表1。

为了验证输入的水位影响因子的多少对水位预测结果产生的影响，接下来增加一个影响因子——流量，即把模型变为双输入单输出(水位和流量—水位)。

3.4 双输入单输出水位预测模型(水位和流量—水位) 首先进行核函数的选取，该研究选择RBF核函数;然后确定γ和σ22个参数。根据参考文献［8］，采用网格搜索法寻找最优参数，最终确定 γ=256.7，σ2=300.0。利用2008年7月～2013年7月的数据对模型进行训练后，对2014年7月测试集的数据进行预测，结果见图3。

表1 单输入单输出水位分析

对模型的输出进行分析，结果见表2。

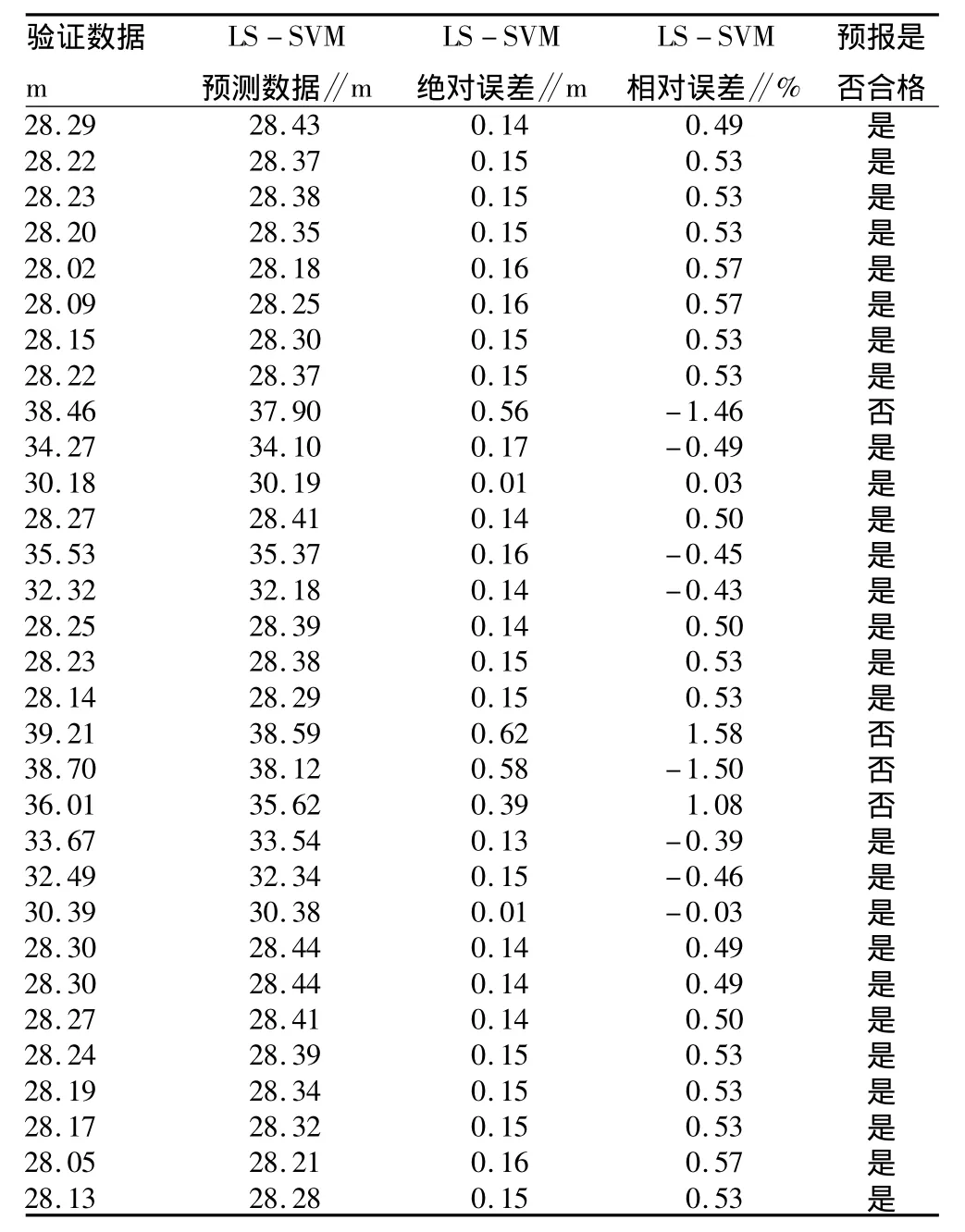
表2 双输入单输出模型水位分析

3.5 结果分析 根据表1、2数据，计算得到2种模型的预测精度:单输入水位预测模型的合格率QR=80.6%，确定系数 DC=0.996 4，GI=94.80%;双输入水位预测模型的合格率 QR=87.10%，确定系数 DC=0.998 5，GI=91.45%。计算表1、2中2种模型的绝对误差与相对误差的平均值，得出如表3所示的2种模型精度对比。

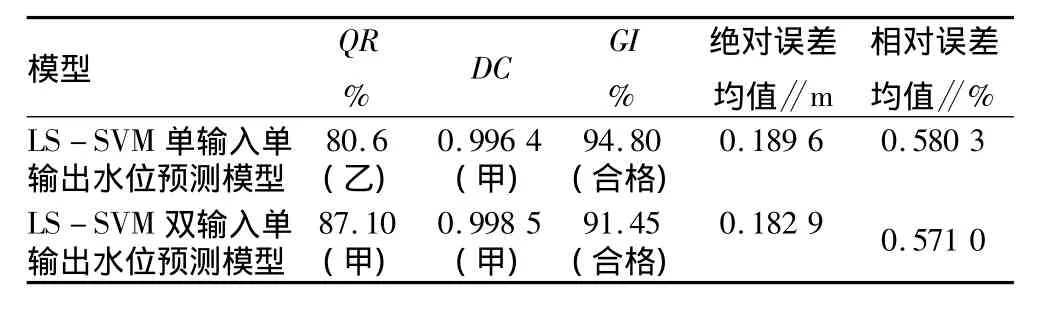
表3 2种模型精度对比

根据表3结果，依据《水文情报预报规范》(SL250－2000)［7］的相关规定可知:通过LS－SVM得到的2种预测模型预测的效果都比较好，均可以用于发布正式的洪水预报。进一步比较得知:基于LS－SVM构建的双输入单输出(水位和流量—水位)预测模型要比单输入单输出(水位—水位)预测模型的预测精度高。也就是说，输入的水位影响因子越多，得到的水位预测模型就会越精确。由于该研究只得到了水位和流量的数据，所以只考虑了水位和流量这2种影响因子，若日后得到其他的水位影响因子的数据，比如河道的断面、降雨量、泥沙量等，就可以得到更加精确的预测模型。

4 结论

该研究应用最小二乘支持向量机(LS－SVM)建立了河道水位预测模型，通过实例分析表明:基于LS－SVM建立的河道水位预测模型是合理可行的，模型的精度等级都达到了乙级以上，可以用于发布正式的洪水预报，这就为农业生产中防洪方案的制定提供了非常有效的支持。由于最小二乘支持向量机需要确定的模型参数仅有γ和σ22个，收敛速度快，预测精度高，因此，LS－SVM的应用前景十分广阔。

［1］ABBOTT M B，BATHURST J C，CUNGE J A，et al.An introduction to the European hydrological system-systeme hydrologique Europeen，“SHE”，2:Structure of a physically-based，distributed modelling system［J］.Journal of Hydrology，1986，87(1):61 －77.

［2］雷晓云，张丽霞，梁新平.基于MATLAB工具箱的BP神经网络年径流量预测模型研究——以塔城地区乌拉斯台河为例［J］.水文，2008，28(1):43 －46.

［3］许剑华.一般线性汇流模型实时预报方法的初步探讨［J］.水利学报，1986(9):72－73.

［4］孙德山，吴今培，侯振挺，等.加权支持向量回归算法［J］.计算机科学，2003，30(11):38 －39.

［5］段华.支持向量机的增量学习算法研究［D］.上海:上海交通大学，2008.

［6］李方方，赵英凯，颜昕.基于Matlab的最小二乘支持向量机的工具箱及其应用［J］.计算机应用，2006，26(S2):358 －360.

［7］中华人民共和国水利部.SL250－2000水文情报预报规范［S］.北京:中国水利水电出版社，2000.

［8］宋小杉，蒋晓瑜，罗建华，等.基于类间距的径向基函数－支持向量机核参数评价方法分析［J］.兵工学报，2012，33(2):203－208.