矩阵方程(AX,YA)=(B1,B2)的埃尔米特广义反汉密尔顿半正定解
杜玉霞,梁 武,汪洪燕
宿州学院数学与统计学院,安徽宿州,234000
矩阵方程(AX,YA)=(B1,B2)的埃尔米特广义反汉密尔顿半正定解
杜玉霞,梁武,汪洪燕
宿州学院数学与统计学院,安徽宿州,234000
摘要:设J∈Rn×n是给定的正交反对称矩阵,即JJT=JTJ=In,JT=-J。如果矩阵A∈Cn×n满足(1)AH=A,JAJ=-AH;(2)∀x∈Cn,xHAx≥0,则称A为埃尔米特广义反汉密尔顿半正定矩阵,所有n阶埃尔米特广义反汉密尔顿半正定矩阵的集合记为HAH。主要利用矩阵自身的结构研究了矩阵方程(AX,YA)=(B1,B2)在集合HAH中有解的充分必要条件;且在有解时解的表达式为。
关键词:矩阵方程;埃尔米特广义反汉密尔顿矩阵;有解条件
1 问题的提出
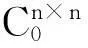
设J∈Rn×n是给定的正交反对称矩阵,即JJT=JTJ=In,JT=-J。如果矩阵A∈Cn×n满足:
(1)AH=A,JAJ=-AH;
(2)∀x∈Cn,xHAx≥0
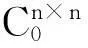
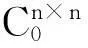
约束矩阵方程问题产生于线性控制领域,它是矩阵计算的一个基本问题,已被广泛研究, 并得到了许多重要的结论,见参考文献[1-6]。文献[1]研究了线性方程AX=B的埃尔米特广义反汉密尔顿半正定解,本文主要利用矩阵自身的结构研究矩阵方程(AX,YA)=(B1,B2)具有反埃尔米特广义汉密尔顿半正定解的充分必要条件及其在有解时解的表达式。
2 相关引理

引理1[1]令:

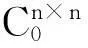

A=YZ++(YZ+)H(In-ZZ+)+(In-

3 问题求解
定理给定矩阵X,B1∈Cn×m1,Y,B2∈Cm2×n,令矩阵:


X1,X2,Y1,Y2∈Ck×(m1+m2)

=rank(Yi),i=1,2
而且,当上述条件成立时,一般解可表示为:
(1)

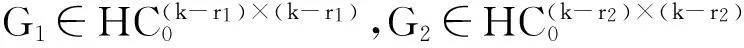

又AH=-A,QHQ=QQH=In








=rank(Yi),i=1,2
而且,一般解可表示为:
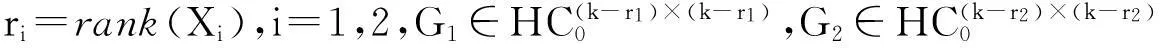
将M1,M2代入引理1中,整理即可得解集合(1)式。
证毕。
参考文献:
[1]张忠志,胡锡炎,张磊.线性矩阵方程的埃尔米特广义反汉密尔顿半正定解[J].数学物理学报,2006,26A(4):612-620
[2]张磊.对称非负定矩阵反问题的可解条件[J].计算数学,1989(11):337-343
[3]袁永新.线性流形上实对称半正定阵的一类反问题[J].高等学校计算数学学报,2000(2):153-158
[4]Xie D X,Zhang L, Hu X Y.The solvability conditions for the inverse problem of bisymmetric nonnegative definite matrices[J].Journal of Computational Mathematics,2000,18(6):597-608
[5]魏平,张忠志,谢冬秀.埃尔米特广义汉密尔顿矩阵的广义逆特征值问题[J].工程数学学报,2010,27(5):820-826
[6]王江涛,张忠志,谢冬秀,等.一类矩阵方程的埃尔米特自反最小二乘解[J].系统科学与数学,2010,30(8):1136-1147
(责任编辑:汪材印)
作者简介:杜玉霞(1981-),女,山东定陶人,硕士,助教,主要研究方向:矩阵方程反问题。
基金项目:安徽省级大学生创新创业训练项目“Matlab辅助线性代数教学及其在实际应用案例中的价值研究”(AH201410379078)。
收稿日期:2015-07-16
中图分类号:O151.21
文献标识码:A
文章编号:1673-2006(2015)10-0094-02
doi:10.3969/j.issn.1673-2006.2015.10.025

