大体积混凝土温升计算方法探讨
刘伟,穆艳君,贾福杰,周良辰,聂凤义,周世玉
(1. 聊城昌润住房开发建设有限公司,山东 聊城 252000;2. 山东聊建集团有限公司,山东 聊城 252000;3. 中国建筑材料科学研究总院 绿色建筑材料国家重点实验室,北京 100024)
大体积混凝土温升计算方法探讨
刘伟1,穆艳君2,贾福杰3,周良辰1,聂凤义1,周世玉1
(1. 聊城昌润住房开发建设有限公司,山东 聊城 252000;2. 山东聊建集团有限公司,山东 聊城 252000;3. 中国建筑材料科学研究总院 绿色建筑材料国家重点实验室,北京 100024)
本文根据某一工程基础筏板大体积施工案例,通过两种计算方法进行大体积温度温升计算,并与实际结构监测结果比较,结果显示,两种方法能够较好的估算最高温度,准确预测最高温度出现时间,可以作为裂缝控制的参考手段之一。
大体积混凝土;温升计算;误差分析
在大体积混凝土施工中,为了控制混凝土的温升,不同的工程师通常会采用不同的方法估算混凝土的温度变化,用来指导施工,以便采取预埋冷却水管等降温以及保温措施。早在 20 世纪 80 年代,《建筑施工手册》[1]就提出了大体积混凝土绝热温升计算公式以及混凝土最高温升计算方法。水工混凝土方面,朱伯芳院士 1999 年在《大体积混凝土温度应力与温度控制》[2]一文中详细阐述了混凝土温度场的计算方法,提出了解析法与有限元计算方法,奠定了我国混凝土温度场计算的基本理论。工民建领域著名裂缝控制专家王铁梦也在 1997 年出版的《工程结构裂缝控制》[3]一书中提出了大体积混凝土温度计算方法及裂缝控制方法。这些方法之间有何差别?它们与工程实测的温度变化的误差有多大?能否指导施工?值得进一步探讨。下面笔者尝试以某一工程基础筏板大体积施工案例,通过两种计算方法进行大体积温度温升计算,并与实际结构监测结果进行比较。
1 工程概况
项目为聊城市昌润住房开发建设有限公司建设的莲湖大厦基础筏板工程,大厦结构体系为框架—核心筒结构。其核心筒基础筏板长 40m,宽 32m,厚度 2.3m,基础筏板混凝土强度等级为 C40,抗渗等级 P8。基础筏板混凝土浇筑为大体积混凝土施工,为避免产生温度开裂,需要对混凝土温升进行计算。
2 混凝土温升计算[4]
下面以笔者亲自测量的工程测温结果为依据,试分析两种温升解析计算方法与实测温度的误差,探讨混凝土温升理论计算方法存在的一些问题。基础筏板施工配合比如表 1 所示,施工期间气温为 20~30℃,环境温度平均温度 25℃。

表1 混凝土施工配合比
从温度控制的角度,需要对混凝土的入模温度和最高温度进行控制,初始温度对混凝土的水化温升速率影响很大,而最高温度决定了混凝土的温升以及后期会产生冷缩温度应力的温差,所以通常要对混凝土的入模温度和最高温度进行计算。
2.1混凝土入模温度估算
根据混凝土搅拌前后热量平衡,得到出机口混凝土温度Ti为:

式中:
Ci——比热,取 Cc=CF=CSL=CH=CS=CG=CAD
=0.837kJ/(kg·℃);
Wi——重量,各种组分重量见表 1 配合比;
Ti——温度,取 Tc=50℃,TF=TSL=TH=TS=TG=25℃,
TW=TAD=15℃。
2.2传统混凝土温升计算方法
根据《建筑施工手册》(第四版)计算如下:
(1)绝热温升

式中:
T——某一龄期的混凝土绝热温升值,℃;
mc——水泥单方用量,kg/m3;
Q——42.5 普通硅酸盐水泥 28d 水化热 375 kJ/kg;
C——混凝土比热,0.96kJ/(kg·K);
ρ——混凝土密度,2400kg/m3;
e——常数,2.718;
t——混凝土的龄期,d;
m——随入模温度变化的系数,查表 2。

表2 系数 m
混凝土龄期 t=∞时,(2) 式中某一龄期混凝土绝热温升值T 即为最大绝热温升 TMAX,据此可以计算绝热温升最大值如下式:
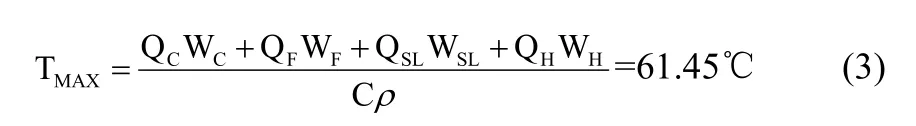
式中:TMAX——混凝土绝热温升最高值,℃;
Q——分别为每千克水泥、粉煤灰、矿粉、HCSA 的水化热量,kJ/kg,日本 Kishi 和 Maekawa 认为粉煤灰的水化热为 209kJ/kg,Bensted 认为粒化高炉矿渣的总水化热值在355~440kJ/kg 范围内,工程所使用的矿渣粉为二级矿渣粉,活性不高,故 QSL应取相对较小的值,这里取 360kJ/kg;
W ——分别为单方混凝土中水泥、粉煤灰、矿粉、HCSA 的用量,kg/m3;
混凝土入模温度估算结果 Tj=23.96℃,根据表 2 用插值法求得 m=0.379。 故得到:

(2)混凝土中心计算温度

式中:
T1(t)——混凝土龄期为 t 时的中心温度,℃;
Tj——混凝土浇筑入模温度,℃;
ξ(t)——t 龄期时的降温系数,根据《建筑施工手册》(第四版)降温系数表,按近似 2.5m 计算。
按照《大体积混凝土温度应力与温度控制》所述,混凝土的最高温度一般龄期 3d 时的温度,本工程 3d 时的计算温度为:
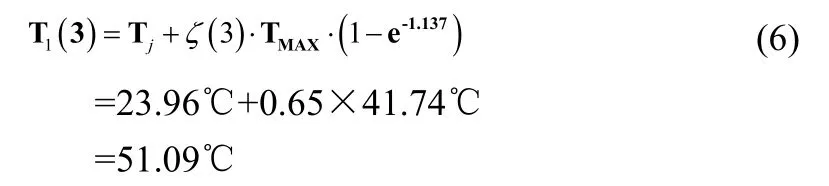
式中:ξ(3)——降温系数,底板属于一维散热,根据龄期和板厚,取 0.65;
同理计算不同龄期时的混凝土中心温度,计算结果见表4。

表4 计算结果
2.3理论解析温升计算方法
根据《大体积混凝土温度应力与温度控制》[2]一书中水化温升的计算方法,考虑到工程结构的实际情况,按第三类边界条件求解混凝土水化热温升,基础筏板以无限大平板计算,底面为绝热,筏板顶面与空气接触,气温 Ta为 0,假设以第三类边界条件处理,可计算如下:
热传导方程:
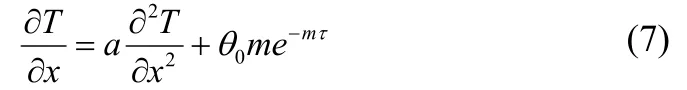
边值条件:τ=0,T=0
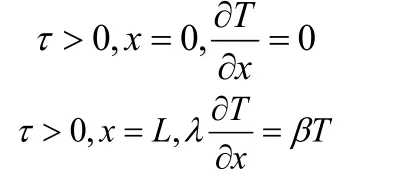
假设初温为 T0,平板无限大并且无热源的,来求解这个方程,设板的厚度为 L,底面为绝热条件,顶面与空气接触,气温 Ta=0,即,

此时,板内平均温度应为,
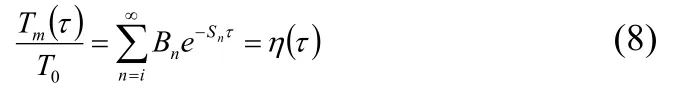
其中,
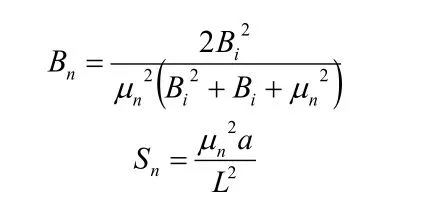
μn为下列特征方程的根,
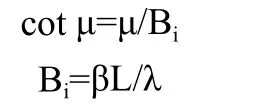
假定在龄期 τ 内有增量 Δθ(τ),它所引起的平均温度升高为 Δθ(τ)η(t-τ)。从 0 到 t 积分,得到平均温度,

基础筏板上表面为第三类边界条件,基础笩板厚度 L 为2.3m,计算虚厚度 λ/β 为 0.1m,比欧准数 Bi=βL/λ=23,导温系数 a=λ/(Cρ)=0.10m2/d,影响系数 m=0.379(1/d),Bn和 Un可根据书 [2] 中表查得,迭代计算结果如表 5 所示,

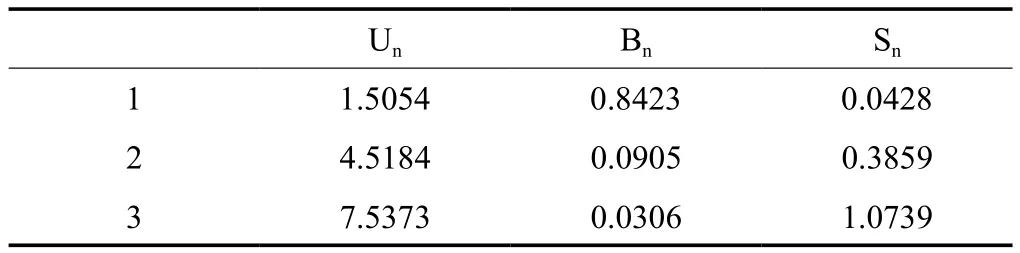
表5 参数迭代计算结果
根据式 (11) 求得混凝土的截面平均温度,

计算结果见表 6。

表6 理论解析法计算结果
3 混凝土温升计算结果讨论
将混凝土实测结果与两种计算方法所得结果作图,如图 1 所示,实测最高温度为 62.8℃,手册法计算最高温度58.14℃,理论解析法计算最高温度 64.47℃,最高温度的误差两种方法分别为 7.4%、2.7%,最高温度出现时间两种方法都相对晚了 3d,这是由于传统计算方法没有考虑水泥细度越来越细,水化速率相比大幅度提高的情况。可以看出,对于最高温的估算,两种方法都能较好的计算出,相比较而言,理论解析法计算的值偏高,并且误差小,偏安全,对于指导大体积工程应用显得更合理一些,而手册所提出的计算方法能考虑到散热条件,对于估算相对体积小一些的混凝土结构具有优势。另外,随着计算机技术和应用的迅速发展,像Ansys、ABAQUS、Marc、MIDAS 等大型有限元软件越来越被大家所接受和使用,日趋完善的有限元分析方法在工程中也得到了越来越广泛的应用,也不失为一个不错的选择。

图1 温度计算结果与实测结果比较
[1] 建筑施工手册[Z].北京:中国建筑工业出版社,2003.
[2] 朱伯芳.大体积混凝土温度应力与温度控制[M].北京:中国电力出版社,1999.
[3] 王铁梦.工程结构裂缝控制[M].北京:中国建筑工业出版社,1997.
[4] 贾福杰.混凝土半绝热温升试验与有限元模拟计算的研究[D].北京:中国建筑材料科学研究总院,2011.
[通讯地址]聊城市经济开发区黄山南路 60 号(252000)
刘伟(1977—),男,工程师。

