不同岩性岩石声发射地应力测试及其应用
彭瑞,孟祥瑞,赵光明,董春亮,左超
不同岩性岩石声发射地应力测试及其应用
彭瑞,孟祥瑞,赵光明,董春亮,左超
(安徽理工大学煤矿安全高效开采省部共建教育部重点实验室,安徽淮南,232001)
为了考虑岩石岩性的影响,对两淮矿区某正在掘进巷道进行钻孔取样,根据柱状图取巷道两相邻水平标高(−850.0 m和−861.8 m,以下称为Ⅰ和Ⅱ水平)作为实验取芯点,其岩性分别为中粗砂岩和砂质泥岩。利用声发射测试仪测得不同水平标高地应力,经理论计算获得相应的主应力,采用ANSYS和FLAC3D在非轴对称应力场(分Ⅰ和Ⅱ水平2种应力加载方法)下进行模拟,并与现场实测结果对比。研究结果表明:Ⅰ和Ⅱ水平的地应力无明显的叠加性。实测巷道不同水平的围岩稳定性(主要指围岩位移分布)与对应水平的应力加载条件下的模拟结果相似;考虑岩石岩性对巷道地应力赋存情况的影响的必要性,同时为该埋藏条件下巷道支护设计提供更加可靠的地应力数据。
岩石岩性;地应力测试;声发射凯赛尔效应;钻孔柱状图;数值模拟;现场实测
地应力是引起地下巷道开挖工程变形和破坏的根本作用力,是进行围岩稳定性分析,实现巷道轴线方向选择、巷道断面形状、支撑设计的必要前提[1−2]。其中地应力测试影响因素的研究及其在各行业中应用情况较多,代表性成果有:探讨断层扰动对地应力测试的影响,并为岩体地下结构稳定性分析、资源开采中岩爆的预测乃至地震的预报与定量评价提供依据[3−4];在非均匀地应力场中,关于巷道围岩稳定性研究[5−7];通过实验测试或理论计算获得某区域地应力场,并利用FLAC3D,模拟该地应力场下[8−13]巷道等建筑结构的稳定性。声发射测试地应力的原理是通过判断Kaiser效应点,进而获得原位岩石的地应力,这项技术在地应力测试领域中,无论是国内还是国外都比较先 进[14−17];很多科研工作者对此项技术进行了不懈地探索;但还需要攻克的难关包括:选取实验测点需考虑的因素、不同角度岩样钻取方法等。本文作者分析岩石岩性对地应力测试的影响。利用钻孔柱状图选取实验点,在实验室中,分别取出巷道相邻2组不同岩性岩石对应的6个方向岩样,经声发射测试仪测试,并根据结果进行计算,获得2组岩性岩石对应埋藏位置处的地应力;获得的地应力测试结果较准确,可真实反映该应力场作用下,无支护巷道开挖面附近围岩的稳定性,从而解决理论分析中,无法充分考虑非均匀应力场(主要指地应力角度、大小的变化),对巷道围岩稳定性影响的问题,以期为矿山等行业提供更加实用、简便的地应力测试方法。
1 地质概况及实验段选取
该矿某掘进巷道附近的岩层钻孔柱状图,如图1所示。从图1可见:巷道地处−852.0 m水平标高,据此选取2个实验点,即在巷道相邻2个水平(Ⅰ水平−850.0 m和Ⅱ水平−861.8 m),分别称为1号测点和2号测点;其中Ⅰ水平对应岩性为中粗砂岩,强度较高;Ⅱ水平对应岩性为砂质泥岩,强度较低。

图1 测点附近的钻孔柱状图
2 实验设计
2.1 测点定向取芯步骤
2.1.1 测点钻孔尺寸和方位选取
在各测点布置一近水平测孔,套取岩芯,钻孔垂直于巷道表面,摆放钻机钻孔,钻孔直径为 90~137 mm,钻孔水平仰角≤5°,3°为最佳水平仰角,在标定待取岩芯之前,先钻取3 m左右的破碎岩芯,既不标定方向也不保留。
2.1.2 定向钻取岩芯的循环操作
首先标定待取岩芯水平方向:假定沿钻孔轴向为方向,垂直钻孔断面为面,向上为方向,水平为方向,利用“岩芯水平定向系统”,对待取岩芯进行水平定向,并建立三维坐标系;接着钻取1 m左右,标定水平方向的岩芯;以后每钻取1 m岩芯,就进行1次水平方向标定,如此循环,直至钻取出7~12 m岩芯;其中“岩芯水平定向系统”是在水准仪的基础上建立的,如图2所示,通过调整带螺纹的套管,将水准仪的水平标记端调整为水平方向;上述方法有效地解决了在深孔中无法直接标记岩芯方向的情况。

图2 巷道断面取芯原理图
2.2 岩样钻取实验
二次定角度钻取岩样:将标定水平方向的岩芯封存后带回实验室,利用钻机和“二次定角度取样装置”,钻取6个方向岩样。图3所示为二次定角度取芯装置。图3(a)所示为实验室传统的取样图,假定圆柱体岩芯的轴向为轴方向,岩芯断面为面,可以钻取,和方向岩样。图3(b)所示为团队自行设计的“二次定角度取样装置及其辅助装置”,获2项专利授 权[18−19]。该装置主要包括:岩芯放置套筒6、槽孔11、支撑架7、装置底座10、岩芯固定装置8;所述岩芯放置套筒6通过焊接方式放置在支撑架7上,所述支撑架7与装置底座10焊接成45°,所述槽孔11处于岩芯放置套筒6内侧,为了避免让钻头1取样时和岩芯放置套筒接触,所述岩芯固定装置8可以通过拧紧一侧的螺母4和螺杆5夹紧岩芯12,并通过一侧的铰接销轴9与岩芯放置套筒6焊接在一起。
利用该“二次定角度取样装置及其辅助装置”的结构特点,通过旋转岩芯12在套筒内的位置,分别在轴夹角、轴夹角、轴夹角角平分线方向(分别标为′,′和′方向)钻取岩样。
在Ⅰ和Ⅱ水平取出的岩芯,通过室内钻取获得的岩样尺寸,如表1所示。

1—钻头;2—夹持板;3—垫板;4—螺母;5—螺杆;6—岩芯旋转套筒;7—支撑架;8—岩芯固定装置;9—铰接销轴;10—装置底座;11—槽孔;12—岩芯
(a) 传统钻取实验;(b) 定角辅助装置钻取实验
图3 二次定角度取芯装置
Fig. 3 Secondary fixed angle coring device

表1 Ⅰ水平和Ⅱ水平各方向岩样的尺寸
2.3 声发射Kaiser测试地应力
采用RMT−150B岩石力学实验系统配合DS2−8B 增强型声发射系统,对实验室取出的2组6个方向岩样进行实验,采用位移控制、加载速度为0.005 mm/s的单轴加载方式;声发射传感器采用声发射放大器、信号滤波器,放大器增益为40 dB,频率为5~1 500 kHz,采样频率为2 500 kHz,参数间隔为200 μs,传感器拾取的声发射信号经前置放大和主放后由声发射仪进一步处理成声发射参数(事件累计、事件速率、能量计数、能量累计等)。根据实验需要采集RMT−150B岩石力学实验系统的轴向力与时间,DS2−8B增强型声发射系统的压力与声发射数,确定岩石时间的凯塞效应点及对应的轴向力,从而获取2组岩样6个方向应力分量,其实测图和原理图如图4所示,加载后Ⅰ和Ⅱ水平对应的破坏岩样如图5所示。
2.4 各方向岩样地应力测试参数
根据岩石的Kaiser效应严格存在于岩石变形的弹性阶段,记忆的最大应力不超过破坏应力的50%的特点,首先由岩石试件的应力−应变关系曲线获得岩样的弹性范围,并将岩样的声发射特征(能量计数、能量计数)−时间的关系曲线进行对比,再结合声发射计数累积曲线,将具有相同特征的突变点确认为Kaiser效应点。

图4 岩石加载及声发射监测系统示意图

(a) Ⅰ水平中粗砂岩;(b) Ⅱ水平砂质泥岩
图6所示为Ⅰ水平′方向的应力−应变关系,图7所示为Ⅰ水平′方向正应力、能量计数及累积与时间关系。由图6可知:Ⅰ水平′方向岩样在单轴加载过程中,当轴向应变在0~0.003范围之内时,岩样处于弹性状态,对应的正应力范围是9.84~25.00 MPa;此时由图7可知:弹性加载的时间范围是36.28~227.87 s。在=42.30 s时,能量计数第1次增大到154,随后在=72.60 s时,发生了较大的突变,且持续时间最长,该点的能量计数最大,所以该点即为Kaiser点,对应的正应力为25.65 MPa。通过上述分析方法,判别Ⅰ和Ⅱ水平附近各方向岩样Kaiser点对应的正应力,如表2所示。
2.5 主应力的计算及其应用
图8所示为岩样各方向正应力分量坐标系。主应力的理论公式推导如下:


图7 Ⅰ水平z′方向正应力、能量计数及累积与时间关系

表2 Ⅰ和Ⅱ水平附近各方向岩样的正应力
注:σ′,σ′和σ′分别为′,′和′方向的正应力。

图8 岩样各方向正应力分量坐标系
从式(1)可以得出:在直角坐标系下,测点处的6个应力分量分别为,,,,和。
某点应力状态的特征方程为
其中:
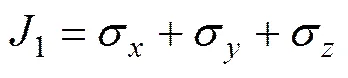

根据式(2)计算的主应力,结合表2中的各方向应力,求解方程组(3),即可得出对应的主应力方向与坐标轴间的夹角余弦。
求解方程组(4)时,结合方程组(3)获得的夹角余弦值l,m和n,可得主应力与坐标正向之间的夹角,同理可以求得主应力与轴、轴正向的夹角。
根据上述理论推导,获得Ⅰ和Ⅱ水平对应的地应力赋存情况如表3所示。

表3 Ⅰ和Ⅱ水平岩样对应的主应力

图9 o测点处的主应力分析
式(5)即为地下岩体测点处的地应力椭球基本方程。将表3所示的计算结果代入式(5)中,就可得到Ⅰ水平中粗砂岩和Ⅱ水平砂质泥岩中岩体地应力椭球表达式。
3 Ⅰ和Ⅱ水平应力加载下的巷道数值模拟
3.1 模拟方案
根据Ⅰ和Ⅱ水平附近岩层钻孔柱状图,由软件AutoCAD按1:1比例画出,导入ANSYS软件建立模型,模型的宽×长×高为60 m×50 m×50 m,长的方向为巷道掘进方向;根据工程实际,设计该掘进巷道巷宽×巷高为5 500 mm×4 250 mm,拱高为2.75 m,直墙高为1.5 m。将建好模型(共有14.29万个单元)导入FLAC3D,生成模型如图10所示,利用FLAC3D进行计算,材料模型设置为Mohr-Cloumb本构模型,具体参数设置根据该矿提供的相关地质资料;其中边界条件设置为:模型侧面限制水平移动,模型底面限制垂直移动,上表面自由;初始应力的设置:依据表2中提供的不同水平的地应力分别进行加载;为了避免边界效应影响,模型的宽、长、高均选为150~200,其中,0为巷道当量半径(即巷道拱高),而0~200范围内的岩石重力相对远场(埋深850.0 m)的初始应力加载可忽略不计。
3.2 计算分析
得到2种应力加载条件下巷道深部围岩位移分布图如图11~12所示。
由图11和图12可知:在Ⅱ水平应力加载条件下获得的巷道底板和两帮的位移明显大于Ⅰ水平条件下获得的位移;其中两帮、底板的位移明显高于顶板位移,这是由于底板和两帮附近围岩为砂质泥岩,其强度较低,属于典型的软岩;这与以往掘进巷道最易发生破坏的经验位置:巷道顶板中间以及其拱肩部情况不相符,表明对现场进行安全性预测,具有复杂性和不确定性。
FLAC3D模拟在Ⅰ水平(或Ⅱ水平)应力加载条件下,巷道深部位移(包括顶板、底板以及两帮)与实测数据(巷道掘进后立即安装多点位移计,测试巷道深部围岩变形情况,包括顶、底板及两帮)进行对比,结果如图13所示。从图13可以发现:FLAC3D在Ⅰ水平应力加载下,巷道顶板位移与实测巷道顶板位移较吻合,同时FLAC3D在Ⅱ水平应力加载下,巷道底板以及两帮位移与实测的底板、两帮位移接近;而FLAC3D在Ⅰ水平应力加载下的两帮位移(见图13),与实测相应位置的位移相差较大。

图10 数值分析模型

数值表示岩层移动位移,单位:cm (a) 巷道两帮位移;(b) 顶板位移

数值表示岩层移动位移,单位:cm (a) 巷道两帮位移;(b) 底板位移
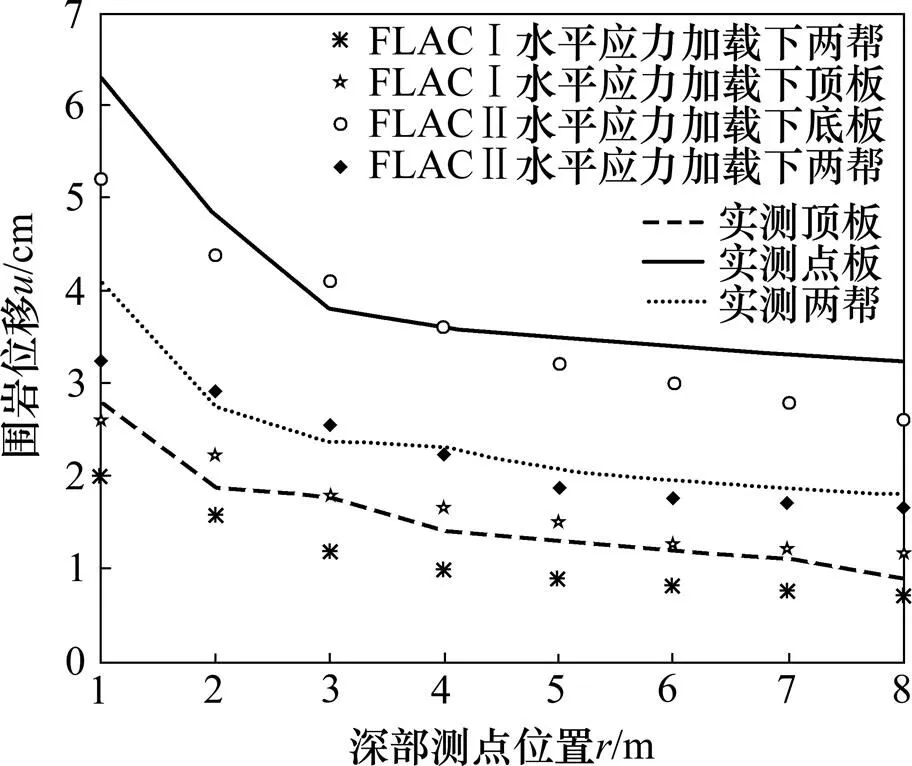
图13 数值模拟与现场实测的数据对比
4 结论
1) 结合室内测试、理论计算、数值模拟以及实测数据,利用声发射系统、ANSYS和FLAC3D软件以及多点位移计等,真实地表现了复杂埋藏条件下(岩石岩性、非轴对称应力场)巷道围岩的稳定性的概况,以期为同样埋藏条件下的地应力测试及其应用提供可靠的工程类比。
2) 沿巷道径向延深,围岩移动位移减小,8 m以外的岩层趋于稳定;Ⅰ水平应力加载条件下,巷道顶板位移与实测顶板位移较吻合;Ⅱ水平应力加载条件下,两帮及底板的位移与实测相应位置位移基本相同。因此,需分别对不同岩性埋藏处进行地应力的测量。
3) 不同岩性岩样对应的地应力测试结果相差较大,所以不能简单地利用重力分布原则进行计算;需针对不同情况细化讨论,如巷道埋藏在均值、各向同性的弹性体中,可以依据重力叠加原理,计算其他水平应力;若巷道是过断层布设,则需对断层上、下盘分别进行测试,若上、下盘岩性不是均值弹性体,则要考虑岩石岩性影响。本文中测试的巷道顶板处于中粗砂岩,底板及两帮位于砂质泥岩,所以需要考虑岩石岩性的影响。
[1] 蔡美峰. 地应力测量原理和技术[M]. 北京: 科学出版社, 2000: 1−10. CAI Meifeng. Principle and techniques of in-situ stress measurement[M]. Beijing: Science Press, 2000: 1−10.
[2] 蔡美峰. 金属矿山采矿设计优化与地压控制: 理论与实践[M]. 北京: 科学出版社, 2001: 5−25. CAI Meifeng. Optimization of mining design and control of ground pressure in metal mines: Theory and practice[M]. Beijing: Science Press, 2001: 5−25.
[3] 蔡美峰, 彭华, 乔兰, 等. 瓦富煤矿地应力场分布规律及其与地质构造的关系[J]. 煤炭学报, 2008, 33(11): 1248−1252. CAI Meifeng, PENG Hua, QIAO Lan, et al. Distribution law of in-situ stress field and its relationship to regional geological structures in Wanfu Coal Mine[J]. Journal of China Coal Society, 2008, 33(11): 1248−1252.
[4] 云龙, 郭彦, 双马瑾. 5°拐折断层在黏滑过程中物理场演化与交替活动的实验研究[J]. 地震地质, 2011, 33(2): 356−368. YUN Long, GUO Yan, SHUANG Majin. An experimental study of evolution of physical field and the alternative during stick-slip of 5° bend fault[J]. Seismology and Geology, 2011, 33(2): 356−368.
[5] 彭瑞, 赵光明, 孟祥瑞. 基于D-P准则的非均匀应力场受扰动轴对称巷道安全性分析[J]. 中国安全科学学报, 2014, 24(1): 103−108.PENG Rui, ZHAO Guangming, MENG Xiangrui. Analysis of disturbed axisymmetric roadway safety under non-uniform stress field on D-P criterion[J]. China Safety Science Journal, 2014, 24(1): 103−108.
[6] 潘阳, 赵光明, 孟祥瑞.非均匀应力场下巷道围岩弹塑性分析[J]. 煤炭学报, 2011, 36(S1): 53−57. PAN Yang, ZHAO Guangming, MENG Xiangrui. Under non-uniform stress field of surrounding rock elastic-plastic analysis[J]. Journal of China Coal Society, 2011, 36(S1): 53−57.
[7] 张小波, 赵光明, 孟祥瑞.基于岩石非线性统一强度准则的非均匀应力场中圆形巷道围岩塑性区分析[J]. 安全与环境学报, 2013, 13(3): 202−206. ZHANG Xiaobo, ZHAO Guangming, MENG Xiangrui. Based on the non-uniform stress field of the rock nonlinear unified strength criterion in the circular roadway surrounding rock plastic zone analysis[J]. Journal of Safety and Environment, 2013, 13(3): 202−206.
[8] 张百红, 韩立军, 韩贵雷, 等. 深部三维地应力实测与巷道稳定性研究[J]. 岩土力学, 2008, 29(9): 2547−2555. ZHANG Baihong, HAN Lijun, HAN Guilei, et al. Study of 3D in-situ stress measurement and stability of roadways in depth[J]. Rock and Soil Mechanics, 2008, 29(9): 2547−2555.
[9] 康红普, 林健, 张晓, 等. 潞安矿区井下地应力测量及分布规律研究[J]. 岩土力学, 2010, 31(3): 827−844. KANG Hongpu, LIN Jian, ZHANG Xiao, et al. In-situ stress measurements and distribution laws in Lu’an underground coal mines[J]. Rock and Soil Mechanics, 2010, 31(3): 827−844.
[10] 孔德森, 蒋金泉, 范振忠, 等. 深部巷道围岩在复杂应力场中的稳定性数值模拟分析[J]. 山东科技大学学报(自然科学版), 2001, 20(1): 68−70. KONG Desen, JIANG Jinquan, FAN Zhenzhong, et al. Numerical simulation analysis of deep roadways stability in compound stress field[J]. Journal of Shandong University of Science and Technology (Natural Science), 2001, 20(1): 68−70.
[11] 吴满路, 廖椿庭, 张春山, 等. 红透山铜矿地应力测量及其分布规律研究[J]. 岩石力学与工程学报, 2004, 23(23): 3943−3947. WU Manlu, LIAO Chunting, ZHANG Chunshan, et al. Red through in-situ stress measurement and its distribution of mountain copper mine study[J]. Journal of Rock Mechanics and Engineering, 2004, 23(23): 3943−3947.
[12] 孙玉福. 水平应力对巷道围岩稳定性的影响[J]. 煤炭学报, 2010, 35(6): 891−895. SUN Yufu. Affects of in-situ horizontal stress on stability of surrounding rock roadway[J]. Journal of China Coal Society, 2010, 35(6): 891−895.
[13] 康红普, 林健, 张晓. 深部矿井地应力测量方法研究与应用[J]. 岩石力学与工程学报, 2007, 26(5): 929−933. KANG Hongpu, LIN Jian, ZHANG Xiao. Research and application of in-situ stress measurement in deep mines[J]. Chinese Journal of Rock Mechanics and Engineering, 2007, 26(5): 929−933.
[14] 彭瑞, 赵光明, 孟祥瑞. 采煤工作面支护测试平台设计[J]. 金属矿山, 2014, 43(3): 128−131. PENG Rui, ZHAO Guangming, MENG Xiangrui. Test platform design of the coal mining face support[J]. Metal Mine, 2014, 43(3): 128−131.
[15] 祝方才, 谢学斌. 岩石声发射技术及在地应力测量中的应用探讨[J]. 国外金属矿山, 2000, 24(2): 13−15. ZHU Fangcai, XIE Xuebin. Rock acoustic emission technology and application in the in-situ stress measurement study[J]. Metal Mines Abroad, 2000, 24(2): 13−15.
[16] 田峰亮, 祝方才, 唐文彪, 等. 基于Kaiser效应的地应力测试研究[J]. 湖南工业大学学报, 2012, 26(5): 21−24. TIAN Fengliang, ZHU Fangcai, TANG Wenbiao, et al. In-situ stress test based on Kaiser effect[J]. Journal of Hunan University of Technology, 2012, 26(5): 21−24.
[17] Lavrov A. The Kaiser effect in rocks: Principles and stress estimation techniques[J]. International Journal of Rock Mechanics and Mining Sciences, 2003, 40(2): 151−171.
[18] 彭瑞, 赵光明, 孟祥瑞, 等. 一种实验室钻取岩样的辅助装置: 中国, ZL 201420131946.7[P]. 2014−07−20. PENG Rui, ZHAO Guangming, MENG Xiangrui, et al. A laboratory sample drilled auxiliary device: China, ZL 201420131946.7[P]. 2014−07−20.
[19] 赵光明, 彭瑞, 董春亮, 等.一种地应力测试二次定角度取芯装置: 中国, ZL 201320718709.6[P]. 2014−04−30. ZHAO Guangming, PENG Rui, DONG Chunliang, et al. A perspective of in-situ stress test the secondary core device: China, ZL 201320718709.6[P]. 2014−04−30.
(编辑 罗金花)
Acoustic emission in-situ stress testing of different lithology rock and its application
PENG Rui, MENG Xiangrui, ZHAO Guangming, DONG Chunliang, ZUO Chao
(Key Laboratory of Safe and Effective Coal Mining, Ministry of Education, Anhui University of Science and Technology, Huainan 232001, China)
In order to consider the influence of rock lithology, bore-hole sampling was gotten in the excavation roadway of Huainan and Huaibei mining area, and two adjacent level elevations of tunnel (−850.0 m and −861.8 m, and referred to as Ⅰ, Ⅱ level in the following) were taken as the core site according to the histogram. Rock lithologies were medium coarse sandstone and sandy mudstone, respectively. Acoustic emission testing instrument was used to measure the in-situ stress of different levels of elevation, and then the corresponding main stress through theoretical calculation was obtained. ANSYS and FLAC3Dwere used to simulate in the non axisymmetric stress field and the field measured results were compared. The results show that the in-situ stresses of Ⅰ, Ⅱ level have no obvious superposition. And the field measurement stability of surrounding rock in different level roadway (mainly refers to the distribution of surrounding rock displacement) is similar to the simulation results under the corresponding horizontal stress loading conditions. It is very necessary to accord the rock lithology on the influence of in-situ stress occurrence conditions of roadway, and more reliable in-situ stress data were provided for roadway support design under the same condition.
rock lithology; in-situ stress test; acoustic emission Kaiser effect; drilling histogram; numerical simulation; field measurement
10.11817/j.issn.1672-7207.2015.09.030
TD451
A
1672−7207(2015)09−3377−08
2014−10−31;
2014−12−30
国家自然科学基金资助项目(51374013) (Project(51374013) supported by the National Natural Science Foundation of China)
孟祥瑞,博士,教授,博士生导师,从事矿山压力与控制研究;E-mail: 13964945@qq.com

