新型外包钢—砼组合梁弯剪扭的非线性有限元模拟

高云

摘 要：基于3根新型外包钢-混凝土“T”形截面组合梁在弯剪扭作用下的试验成果，采用ANYSY参数化程序设计语言（APDL）编制了命令流，对弯剪扭作用下组合梁的受扭性能进行了非线性有限元分析（FEM）。FEM分析考虑了钢筋与混凝土间的相互作用以及钢与混凝土间的相互作用，较好地模拟了新型外包钢-混凝土“T”形截面组合梁的受力、破坏全过程，从而验证了运用ANYSY对构件受扭性能进行模拟计算的有效性，为组合梁设计提供了实用的计算软件。

关键词：混凝土；弯剪扭作用；有限元模拟；滑移模型

中图分类号：TU398.9 文献标识码：A DOI：10.15913/j.cnki.kjycx.2015.24.108

新型外包钢-混凝土“T”形截面组合梁是在弥补传统普通工字钢-混凝土组合梁缺点的基础上提出的一种新型组合梁。新型外包钢-混凝土组合梁能充分发挥混凝土抗压强度高、钢材抗拉性能好的优势，组合效应显著。组合梁是一种复合构件，受扭性能非常复杂，国内外对组合梁受扭性能的研究相对较少。本文在试验研究的基础上，采用ANSYS参数化程序语言（APDL）编制了命令流，对不同弯剪扭作用下组合梁的受力性能进行了非线性有限元分析。

1 研究对象

本文选取了弯剪扭作用下的3根组合梁进行分析，3根组合梁的截面尺寸相同。混凝土的实测强度fc=20.4 MPa；钢筋采用Φ6，实测屈服强度fy=345 MPa；钢板采用Q235钢，厚4 mm的钢板实测屈服强度fy=354 MPa，厚8 mm的钢板实测屈服强度fy=288 MPa。

组合梁构件的SBD3弯扭比为1∶1，SBD4弯扭比为3∶1；SBD5弯扭比为5∶1.

2 有限元模型和本构关系

2.1 混凝土和钢筋有限单元模型

混凝土采用ANSYS程序提供的三维八节点实体单元（Solid65）。组合梁中的钢筋采用三维杆单Link8。

2.2 “U”形外包钢与垫块有限单元模型

“U”形外包钢采用Shell181壳单元，而垫块采用三维八节点实体单元（Solid45）。

2.3 外包钢与混凝土的滑移模型

本文采用在外包钢与混凝土界面上栓钉对应节点处设置长度为零的非线性弹簧单元Combin39这一方法来模拟外包钢与混凝土的黏结滑移问题，弹簧的一端连接外包钢板单元节点，另一端连接混凝土单元节点。

2.4 混凝土的本构关系

在ANSYS程序中，利用多线性等向强化模型MISO来表达应力应变关系。

2.5 混凝土的破坏准则

ANSYS中采用的失效模型是William and Warnke五参数强度模型，五个参数由试验确定。混凝土所取有关参数为：开裂剪力传递系数βt=0.5，闭合剪力传递系数βc=1.0，抗拉强度ft=1.941 MPa，单轴抗压强度fc=-1（不考虑混凝土压碎），其他参数采用William and Warnke强度模型的默认值。

2.6 钢筋和“U”形外包钢的本构关系

假设钢筋和“U”形外包钢为理想弹塑性材料，不考虑强化段，则受拉和受压方向相同。本文所采用钢材的泊松比为0.3，抗拉强度与屈服强度取实测值。

此外，混凝土徐变、收缩效应的影响因素较多，表现形式也较为复杂，本文仅讨论短期荷载作用下梁的受扭情况。

2.7 黏结滑移的本构关系

采用如下本构关系：

3 有限元模型的建立和求解

本文根据构件实际情况建立起有限元模型，约束模型一端节点的所有自由度，从而模拟悬臂梁的固定端。在梁的自由端，沿加载钢梁外侧的节点施加节点集中力等效合成扭矩，在底部节点施加向上的节点力模拟施加的弯矩和剪力。同样采用弹簧单元来模拟外包钢与混凝土之间的黏结滑移，不考虑混凝土的压碎情况。

4 有限元分析结果

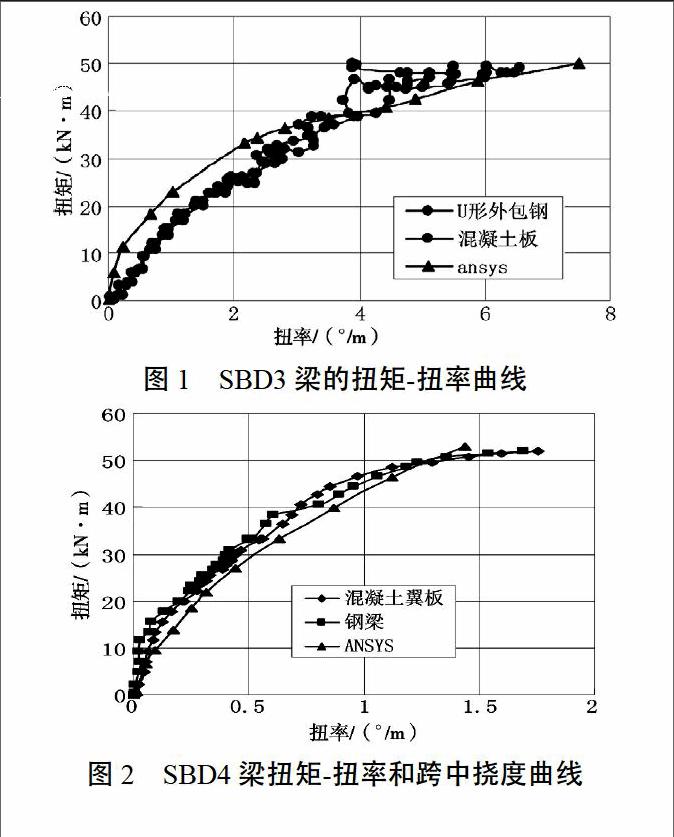
由于篇幅限制，本文仅截取SBD3梁和SBD4梁的部分成果图。SBD3梁的扭矩-扭率曲线如图1所示，SBD4梁扭矩-扭率和跨中挠度曲线如图2所示。

5 结论

本文运用ANSYS软件对新型外包钢-混凝土“T”形截面组合梁在弯剪扭作用下的构件进行了非线性有限元分析，并与实验结果进行了对比，得到如下结论：①非线性有限元数值方法能较好地对新型组合梁的弯剪扭性能进行模拟；②由于对混凝土材料本身性质的模拟与实际情况有一定的差距，而且本文所采用的黏结滑移本构关系与实际滑移的情况也有差距，所以无论是极限荷载，还是变形曲线和试验，均存在一定的误差，因此，需要对混凝土材料性质和滑移的模拟进行进一步的研究。

参考文献

[1]范旭红，石启印，马波.钢-混凝土组合梁的研究与展望[J].江苏大学学报（自然科学版），2004（1）.

[2]石启印，马波，李爱群.新型外包钢-砼组合梁的受力性能分析[J].实验力学，2005（1）.

[3]龚曙光，谢桂兰.ANSYS操作命令与参数化编程[M].北京：机械工业出版社，2004.

[4]郝文化.ANSYS土木工程应用实例[M].北京：中国水利水电出版社，2005.

[5]杨云安，唐家祥，陈光明.粘钢加固钢筋混凝土矩形受扭构件的非线性有限元数值模拟[J].华中科技大学学报（城市科学版），2003（2）.

〔编辑：王霞〕