Global Stabilityfor a Diffusive System with Time Delayand Functional Response

LEI Ming（雷 鸣），JIANG Yuanzheng（姜元政）

School of Mathematics and Statistics，Beihua University，Jilin 132013，China

Introduction

Patch population theory focuses on describing the effect of patch to population's survival and extinction.In recent years，many scholars have been studying the biodynamical system with diffusion by using patch population theory［1-3］.Nowadays，while the economy is developing rapidly，the ecological environment is severely damaged，resulting in population living environment fragmented in isolation.Protecting the wild animals becomes more and more important.In order to protect vulnerable groups，people are taking some measures to provide shelter environment for the endangered populations，such as building corridors or establishing natural protection areas.It has practical significance and important theoretical value to further study the persistence and global asymptotic stability of multigroup diffusion ecosystem in different patch environments.By revealing the evolution rules，the biological diversity can be maintained and strong support for the development and protection of the ecosystem can be provided.It is known that there are few research findings published on the diffusion system with distributed delays and ratio-dependence-type functional response.In this paper，the following diffusion system with functional response and time delay is taken into consideration：

where N1（t）and N2（t）are the densities of the first species in patches I and II at time t respectively，and they can diffuse in patches I and II；N3（t）is the density of the second species in patch I at time t；D1（t）and D2（t）are their diffusion coefficients；ai（t），bi（t），βi（t），cj（t），Dj（t），α（t）∈C（R，R＋）（i＝1，2，3，j＝1，2），and they are continuous，bounded and strictly positive functions about t in R＋＝［0，＋∞）；time delayτ＞0；φ（N1（t））＝c1（t）N1（t）／（α（t）N1（t）＋N3（t））is the ratio-dependen type functional response；and Kiis the measurable and normalized

Denote

Let C＋＝C（［-τ，0］，）denote all continuous vector functions from［-τ，0］to.From the applicable quality of system（1），the initial value problem is considered in this paper：

whereφi∈C＋，Ni（s）＝φi（s）≥0，and s∈［-τ，0］（i＝1，2，3）.Based on the ecological meaning of the system，system（1）is considered only in int.To continuous and

bounded function f（t），denote

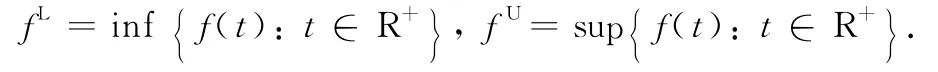
Further，denote

1 Persistence

Definition 1 If there exists a compact region D ⊂int，making every solution of system （1）which satisfies the initial value condition（2）ultimately enter and remain in region D，then system（1）is uniformly persistent.

Proof Proof method is similar to Refs.［4-7］，hence the proof is omitted.

Lemma 2 Suppose（N1（t），N2（t），N3（t））Tis an arbitrary positive solution of system （1）which satisfies the positive initial value condition（2）.If

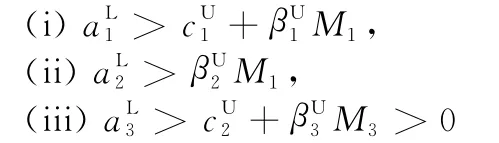
hold，then there exists T ＞0；when t≥T，follow

m1≤Nj（t）≤M1（j＝1，2），m2≤N3（t）≤M2.

Proof Suppose（N1（t），N2（t），N3（t））Tis an arbitrary positive solution of system（1）.Set

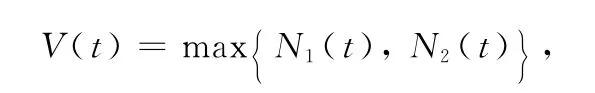
from the first and the second equations of system（1），D＋V（t）≤V（tis obtained，namely

From the third equation of the system，when t＞T1＋τ，follows

Similarly，there exist T2＞T1＋τand M2≥；make t≥T2，then N3（t）≤M2.

Similarly，from the third equation of the system，we havenamely

And there exist T4＞T3and≥m2＞0；make t≥T4，then N3（t）≥m2.

Set T ＝T4，and when t≥T，follow

The proof is complete.

According to the above，Miand mi（i ＝1，2）exist，and they don't depend on any positive solution of system（1）；compact set

is a positively invariant set and an ultimate bounded region of system （1），where M ＝m ＝minHence，the following theorem is obtained im-mediately.

Theorem 1 If system （1）satisfies the positive initial value condition（2）and the condition of Lemma 2，then system（1）is uniformly persistent.

2 Existence of Positive Periodic Solutions

Supposing ai（t），bi（t），βi（t），cj（t），Dj（t），α（t）∈C（R，R＋）are all continuously positive periodic functions with periodicω，then system（1）isω-periodic system.By using the continuation theorem of Gaines and Mawhin［4］，the theorems below are proved.

Lemma 3 Let X and Z be Banach spaces，let L be a Fredholm mapping of index zero and let N：compact on，whereΩ⊂Xis an open bounded set.Suppose

（a）Lx ≠λNx，∀x ∈∂Ω ∩Dom L，λ ∈（0，1）；

（b）QNx ≠0，z ∈∂Ω ∩Ker L；

Then the equation Lx ＝Nx has at least one solution in∩Dom L.

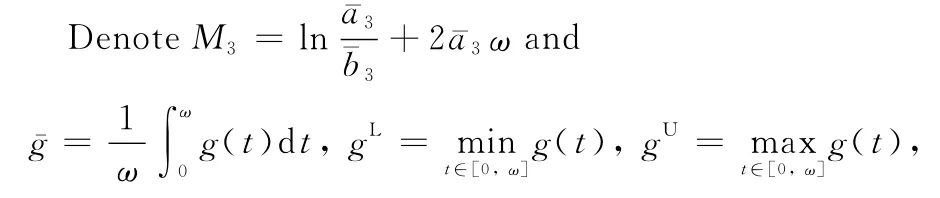
where g（t）is a continuousω-periodic function.

Theorem 2 If

then the periodic system（1）has at least one positiveω-periodic solution.

Proof Make the change of variables Ni（t） ＝then system（1）can be reformulated as

where

In order to apply Lemma 3 to system（1），define

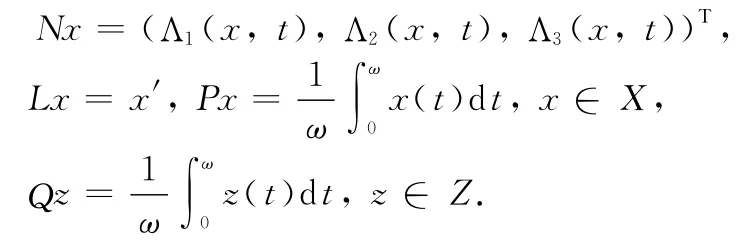
where

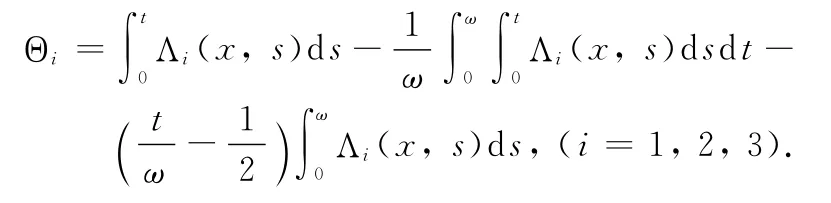
Obviously，QN and KP（I-Q）Nare continuous.It is not difficult to show thatis compact for any open boundedΩ ⊂X by using Arzela-Ascoli Theorem.Moreover，QN）is clearly bounded.Thus，N is L-com-pact onwith any open bounded setΩ ⊂X.

Now，search for an appropriate open bounded subsetΩ for the application of the continuation theorem（Lemma 3）.From the operator equation Lx ＝λNx，λ ∈（0，1），follow

Assume that x＝x（t）∈Xis theω-periodic solution of system（4）for a certainλ ∈（0，1），thenηi，ξi∈［0，ω］（i＝1，2，3）exist，such that xi（ηi）＝xi（t），xi（ξi）＝xi（t），therefore，x′（η1）＝0，x（η2）＝0.Further，follow

If x1（η1）≥x2（η2），then x1（η1）≥x2（η1），by Eq.（5），follows

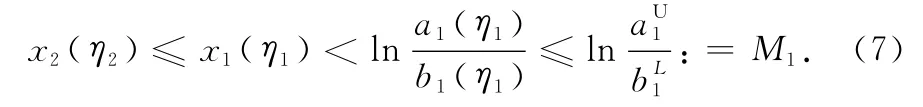
If x1（η1）＜x2（η2），then x1（η2）＜x2（η2），by Eq.（6），follows

Integrate from 0toωon both sides of the third equation of system（4），follows

By Eq.（9），follows

Again from Eq.（9），follows

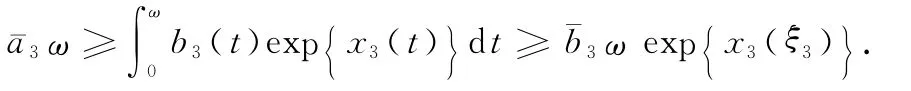
It is easy to check that

Thus，from Eqs.（10）and（11），for any t ∈［0，ω］，follows

Also，by Eq.（9），follows

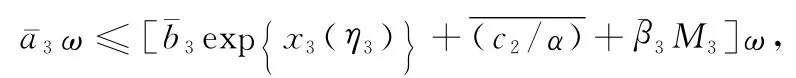
namely

By Eqs.（10）and（13），for any t∈［0，ω］，it then follows

From Eqs.（12）and（14），follows

Now，take ξi∈ ［0，ω］，such that xi（ξi） ＝xi（t），i＝1，2，3.Then followx′i（ξi）＝0，i＝1，2，3.Further，we can obtain

If x1（ξ1）≥x2（ξ2），then x1（ξ2）≥x2（ξ2），by Eqs.（17）and（8），follows

If x1（ξ1）＜x2（ξ2），then x1（ξ1）＜x2（ξ1），by Eqs.（16）and（7），follows

By Eqs.（7），（8），（18），and（19），we obtain

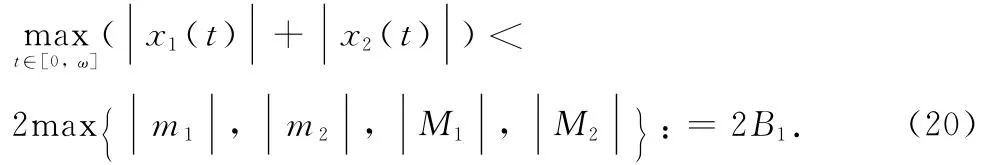
Therefore Eqs.（15）and（20）yield that

where（x1，x2，x3）T∈R3，t0，t1∈［0，ω］，andμ ∈［0，1］.For any solutionof system （22），μ ∈［0，1］，there exists 0＜B0＜＋∞such that

Obviously，B1，B2，and B0are not dependent on the parameterλ.thenΩsatisfies the condition（a）of Lemma 3，where x ∈∂Ω ∩Ker L ＝∂Ω ∩R3，xis a constant vector in R3with‖x‖＝B，then QNx≠0.Thereby this satisfies condition（b）of Lemma 3.Now consider mapping

From Eqs.（21）and（23），we will prove hμ（x）is a homotopy mapping，namely to prove when x ∈∂Ω ∩Ker L，then hμ（x）≠0，take mapping J＝I：ImL→Ker L，x→x，follows

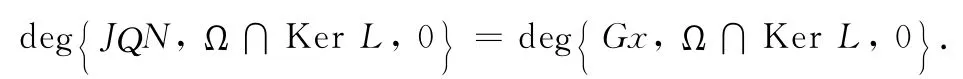
Under the assumptions in Theorem 2，it is easy to show that the system of algebraic equations

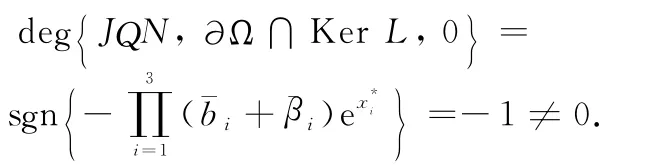
This proves thatΩsatisfies condition（c）of Lemma 3.The proof is complete.

3 Global Attractivity

Lemma 4（Barbalat Lemma［5-10］）Supposing t0≥0and fis nonnegative function defined in［t0，＋∞），it is integrable and uni-formly continuous in［t0，＋∞），then follows

Theorem 3 System（1）satisfies positive initial value condition（2）and conditions of Theorem 2，if

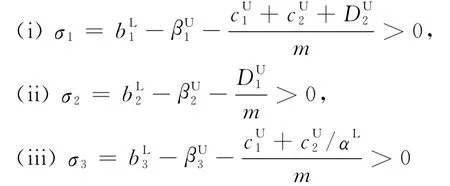
hold，then system（1）has a unique positive solution which is globally asymptotically stable（namely global attractivity）.

Proof Suppose（N1（t），N2（t），N3（t））Tis a positive periodic solution of system （1）andis an arbitrary positive solution of system （1）.From uniform persistence of system（1），we know that there exists T ＞0，when t＞T，and follow m ≤Ni（t），（t）≤M，i＝1，2，3.So，define Lyapunov Function：

Notice that

Estimate the right upper derivative of V（t）along the solutions of system（1），we obtain that：

Integrating both sides of the above formula fromTto t，we getV（T）＜＋∞.So

From the uniform persistence and derivative boundedness of positive periodic solution of system （1），we knowis uniformly continuous in［T，＋∞），then fromLemma 4，we know

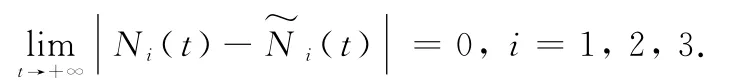
The proof is complete.

4 Conclusions

The population's intrinsic rate of increase and natural mortality rate are two important control parameters.If the intrinsic rate of increase of each population is large enough，we know the system is uniformly persistent by Lemma 2，namely the two competing populations persistently exist；if the intrinsic rate of increase of each population is larger than the dissipation rate，then by Theorem 1 we know the system has at least one positive periodic solution，namely the two competing populations also persistently exist in a periodic environment；if the two competing populations'total dissipation，including predation rate，genetic effect and diffusion rate，is far below its natural mortality rate，then，by Theorem 3 we know the positive periodic solution of the system is globally asymptotically stable，namely in a periodic environment the two competing populations will continue to exist and multiply in a stable situation.To protect biodiversity in patches of habitat，the population intrinsic rate of increase and natural mortality rate of each population are two critical control parameters.

［1］Huang Y M.Global Stability for a Diffusive Model with Time Delay and Functional Response［J］.Journal of Biomathematics，2006，21（3）：370-376.

［2］Chen F D.Global Asymptotic Stability in n-Species Non-autonomous Lotka-Volterra Competitive Systems with Infinite Delays and Feedback Control［J］.Applied Mathematics and Computation，2005，170：1452-1468.

［3］Zhao M，Cheng R F.Existence of Periodic Solution of a Food Chain System with Biocontrol and Ratio Functional Response［J］.Journal of Jilin University：Science Edition，2009，47（4）：730-736.

［4］Gaines R E，Mawhin J I.Coincidence Degree and Nonlinear Differential Equations［M］.Berlin：Springer-Verlag，1997：40-45.

［5］Feng Y Q，Li S G.Existence of Positive Periodic Solutions to a Second-Order Differential Inclusion［J］.Annals of Differential Equations，2012，28（1）：26-31.

［6］Gao L L，Wang L L.Multiple Periodic Solutions to Second Order Functional Differential Equation with Infinite Delay［J］.Annals of Differential Equations，2012，28（1）：32-37.

［7］Yoichi E，Ynkihiko N，Yoshiaki M.Global Stability of SIRS Epidemic Models with a Class of Nonlinear Incidence Rates and Distributed Delays［J］.Acta Mathematica Scientia，Series B：English Edition，2012，32（3）：851-865.

［8］Barbalat I.Système d'équation Différentille d'Oscilltion Nonlinéaires［J］.Romanian Journal of Pure and Applied Mathmatics，1959，4：267-270.

［9］Fu Y，Qu C Z.Unique Continuati on and Persistence Properties of Solutions of the 2-Component Degasperis-Procesi Equations［J］.Acta Mathematica Scientia，2012，32（2）：652-662.

［10］Zhao X，Li J P，Zhang W J.Summer Persistence Barrier of Sea Surface Temperature Anomalies in the Central Western North Pacific［J］.Advances in Atmospheric Sciences，2012，29（6）：1159-1173.