TrainingRobust Support Vector Machine Based on a New Loss Function

LIU Yeqing（刘叶青）

School of Mathematics and Statistics，Henan University of Science ＆Technology，Luoyang 471003，China

Introduction

Support vector machine （SVM）［1］was introduced by Vladimir Vapnik and colleagues.It is a relatively new learning method used for data classification.The basic idea is to find a hyperplane which separates the d-dimensional data perfectly into its two classes.Since example data were often not linearly separable，the notion of a“kernel induced feature space”was introduced which mapped the data into a higher dimensional space where the data were separable.Typically，casting into such a space would cause overfitting and calculation problems.The key technique used in SVM is that the higher-dimensional space doesn't need to be dealt with directly（as it turns out，only the formula for the dotproduct in that space is needed）， which eliminates overfitting and calculation problems.Furthermore，the VCdimension（a measure of a system's likelihood to perform well on unseen data）of SVM can be explicitly calculated，unlike other learning methods such as neural networks，for which there is no measure.Overall，SVM is intuitive，theoretically well-founded，and has shown to be practically successful.

SVM has been receiving increasing interest in many areas as a popular data classification tool.Unfortunately，researchers have shown that SVM is sensitive to the presence of outliers even though the slack technique is adopted.The central reason is that outliers are always playing dominant roles in determining the decision hyperplane since they tend to have the largest margin losses according to the character of the hinge loss function.

In machine learning，the hinge loss is a loss function used for training classifiers.The hinge loss is used for the“maximum-margin”classification，most notably for SVM.For an intended output yi＝±1and a classifier score f（xi）＝wxi＋b，the hinge loss of the prediction f（xi）is defined as l（yi·f（xi））＝max（0，1-yi·f（xi））.It can be seen that when yiand f（xi）have the same sign，this means that f（xi）predicts the right class and｜f（xi）｜≥1，l（yi·f（xi））＝0，but when they have opposite sign，l（yi·f（xi））increases linearly with f（xi）（one-sided error）.SVM uses linear hinge loss function［2］.According to the character of the linear hinge loss function，SVM is sensitive to outliers.In addition，the linear hinge loss function was not smooth.Thus， when used in SVM，it degrades the generalization performance of SVM.

In this paper a new tangent loss function was proposed.As the tangent loss function was not smoothing in some interval，a polynomial smoothing function was used to approximate it in this interval.Based on the tangent loss function，the tangent SVM （TSVM）was proposed.The experimental results show that TSVM reduces the effects of outliers.So the proposed new loss function is effective.

1 Related Works

Consider a binary classification problem.Given a training dataset，where xi∈ℝnand yi∈｛-1，＋1｝.The primal optimization of SVM is usually written as：

where C ＞0is a penalty parameter；H1（u）is the linear hinge loss function，which has the form of H1（u）＝max（0，1-u）.It is obvious that the linear hinge loss function has no limit on the loss values of outliers，whose loss values may be very large when yi（w·xi＋b）≪1.Thus，of all training samples，the outliers will retain the maximal influences on the solution since they will normally have the largest hinge loss.This results in the decision hyperplane of SVM being inappropriately drawn toward outliers so that its generalization performance is degraded.

Many loss functions［3-11］have been proposed to improve the generalization performance，increase the speed of optimization problem solving， or account for certain nonstandard situations.

Lee and Mangasarian［3］proposed quadratic hinge loss function，

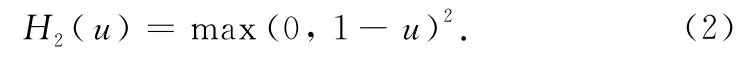
Though quadratic hinge loss function is smooth，it enhances greatly the loss values of outliers.

Shen et al.［7］proposed a new method that replaced the hinge loss in SVM by a loss function of the form，

Although their method［7］outperforms SVM in nonseparable cases，the method is computationally much more complex than SVM.

Lin et al.［8］extended SVM to nonstandard situations by adding an extra term to the hinge loss

Here the extra termc（y）reflects two types of nonstandard situations：（1）misclassification costs are different for different classes，and（2）the sampling proportions of classes are different from their population proportions due to sampling bias.

The above loss functions penalize only points with u ＜1.As a result，they all have the same problems as SVM，namely，they are sensitive to training samples and perform poorly.

The Ramp loss function

was used in SVM recently［5-6］.The Ramp loss function has been investigated widely in the theoretical literature in order to improve the robustness of SVM，which limits its maximal loss value distinctly.Obviously，the Ramp loss function can put definite restrictions on the influences of outliers so that it is much less sensitive to their presence.Though the Ramp loss function limits the loss values of outliers，the losses caused by outliers are the same as those caused by any other misclassified samples.Thus，all misclassified samples are considered the same.Obviously，outliers and support vectors could not be treated equally.

2 Tangent Loss Function

To robustify the SVM，a new loss function is proposed.We call it tangent loss function，which has the form，

The value of the function T（u）is in the interval［0，2）.It is apparent that the loss function T（u）limits loss value of outliers.However，the tangent loss function is not smooth when u＝1，and a polynomial function is used as the smooth approximation for T （u ） in the intervalwhere k ＞0.Thus，T（u）changes into a new smoothing loss function S（u）（see Fig.1），

Thus，under the smoothing loss S（u），optimization problem（1）changes into the following problem，

We call this SVM as TSVM.

3 Experiments

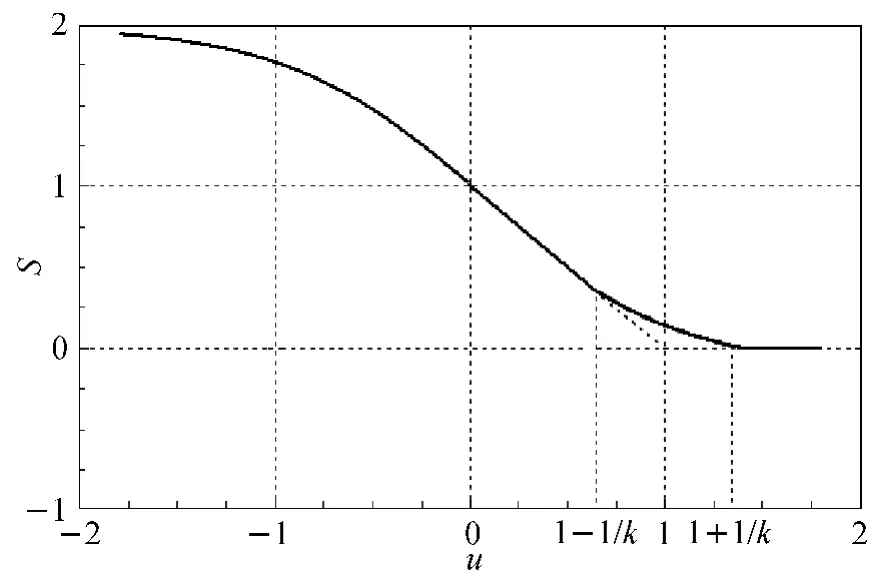
Fig.1 The function image of S（u）

To verify the efficiency of the tangent loss function，experiments are performed on UCI data sets.We compare TSVM with SVM，which use the loss function of H2（u）.Because the H2（u）quadratic hinge loss function is smooth function，the corresponding optimization problem can be solved directly.If we use the linear loss function H1（u），then the corresponding optimization problem can be solved only after being approximated using a smooth function.BFGS algorithm was used to solve the optimization problem（2）.The algorithms are written in Matlab7.1，k ＝25，and other parameters are chosen for optimal performance.

We demonstrate the effectiveness of the TSVM by comparing it numerically with SVM on UCI data sets.

Those data sets include moderate sized data sets，monks-1，monks-2，breast-w，heart-statlog；balance and large data sets magic gamma telescope.In data sets monks-1 and monks-2，the training samples are draw-out from the testing samples.Their training samples are fixed.In other data sets，the training samples are chosen randomly，the remaining samples are testing samples.In the latter data sets，to demonstrate the capability of TSVM，training set sizes change.We performs 5-fold cross validation on each data set.Table 1shows the results of TSVM and SVM according to average testing accuracy，and p，q，and k are the numbers of training samples，testing samples，and outliers，respectively.

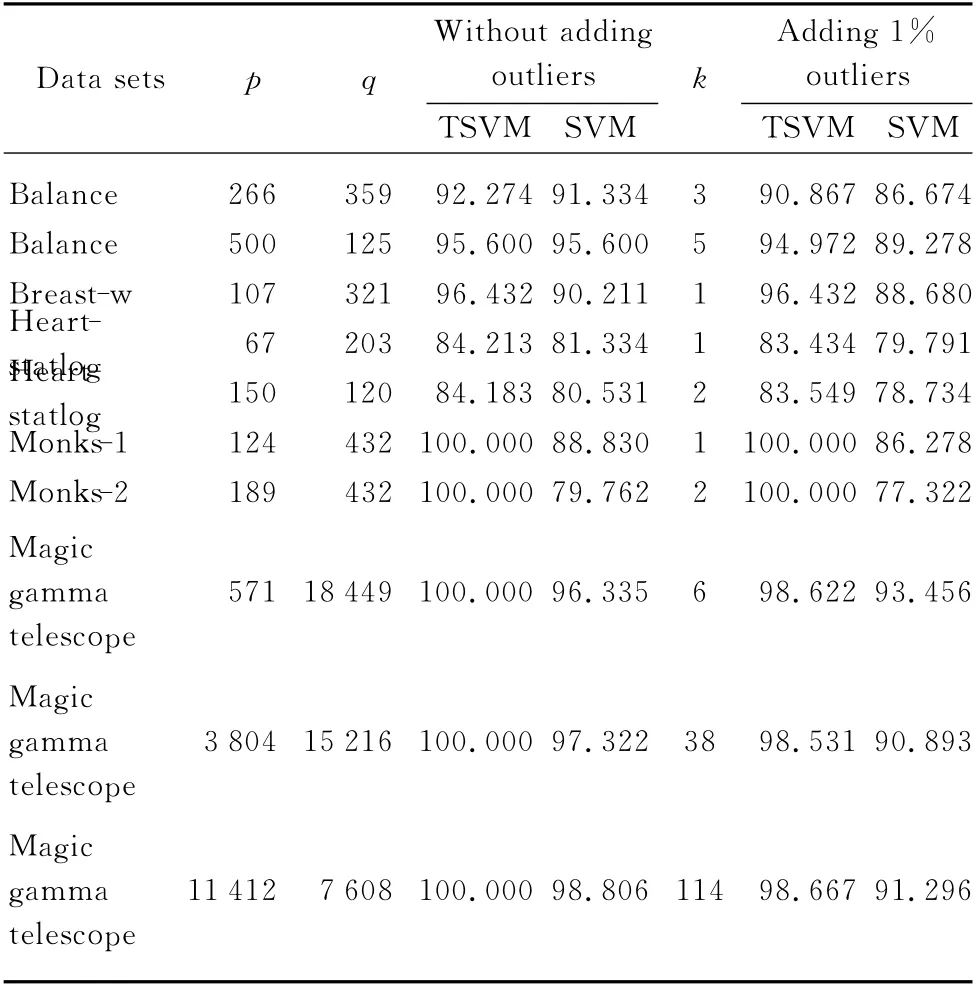
Table 1 Comparing the testing accuracy of TSVM and SVM

In order to compare the robustnesses of TSVM and SVM，we repeat above experiments on these training sets by adding 1% outliers.The outliers are produced by changing their labels.TSVM and SVM learn classification on such new training sets.The experimental results are also reported in Table 1.It is obvious that testing accuracy of TSVM is higher than that of SVM on all data sets.As a result of adding 1% outliers to the datasets，the testing accuracy of TSVM decreases no more than 1.5% while that of SVM decreases much more significantly by about 1.5%-7.5%.

The experimental results show that TSVM is effective and is more robust to outliers than SVM.

4 Conclusions and Future Research

Because of using hinge loss function，conventional SVM is sensitive to outliers.A new loss function-tangent loss function was proposed.Since the tangent loss function was not smooth， a smoothing function was adopted to approximate it.The experimental results show the tangent loss function is more robust to outliers than linear hinge loss function.Therefore，the proposed new loss function is effective.

There are several other research directions that need to be further pursued.Such as comparison with other large margin classifiers and other approaches to large sample bias problems would be interesting and generalized to nonlinear kernel functions needs to be investigated in the future.

［1］Vapnik V.Satistical Learning Theory［M］.New York：Wiley-Interscience，1998.

［2］Chapelle O.Training a Support Vector Machine in the Primal［J］.Neural Computation，2007，19（5）：1155-1178.

［3］Lee Y J，Mangasarian O L.SSVM：a Smooth Support Vector Machine for Classification［J］.Computational Optimization and Applications，2001，22（1）：5-21.

［4］Wang S C，Jiang W，Tsui K L.Adjusted Support Vector Machines Based on a New Loss Function［J］.Annals of Operations Research，2008，174（1）：83-101.

［5］Xu L，Crammer K，Schuurmans D.Robust Support Vector Machine Training via Convex Outlier Ablation ［C］.Proceedings of the 21st National Conference on Artificial Intelligence，Boston，2006：1321-1323.

［6］Wang L，Jia H D，Li J.Training Robust Support Vector Machine with Smooth Ramp Loss in the Primal Space［J］.Neurocomputing，2008，71（479）：3020-3025.

［7］Shen X，Tseng G C，Zhang X，et al.Onψ-Learning［J］.Journal of American Statistical Association，2003，98（463）：724-734.

［8］Lin Y，Lee Y K，Wahba G.Support Vector Machines for Classification in Nonstandard Situations ［J］.Machine Learning，2002，46（2）：191-202.

［9］Wu Y C，Liu Y F.Non-crossing Large-Margin Probability Estimation and Its Application to Robust SVM via Preconditioning［J］.Statistical Methodology，2011，8（1）：56-67.

［10］Ertekin S，Bottou L，Giles C.Nonconvex Online Support Vector Machines［J］.IEEE Transactions on Pattern Analysis and Machine Intelligence，2010，33（2）：368-381.

［11］Zhong P.Training Robust Support Vector Regression with Smooth Non-convex Loss Function［J］.Optimization Methods＆Software，2012，27（6）：1039-1058.