Cryptanalysis of a Completely Anonymous Multi-recipient Signcryption Scheme with Public Verification

ZHANG Bo（张 波），SUN Tao（孙 涛），YU Dairong（于代荣）

1 School of Information Science and Engineering，University of Jinan，Jinan250022，China

2 Shandong Provincial Key Laboratory of Network Based Intelligent Computing，Jinan250022，China

3 Shandong Provincial Key Laboratory of Software Engineering，Jinan250101，China

Introduction

Identity-based （ID-based） cryptosystems［1］were proposed to solve the problem of management of public key certificates.Its main idea is that the public keys of a user can be easily derived from arbitrary strings corresponding to his identity information such as name，telephone number，and email address.The corresponding private key can only be derived by a trusted private key generator（PKG）.By combining ID-based cryptology and signcryption，Malone-Lee［2］gave the first ID-based signcryption scheme.Since then，quite a few ID-based signcryption schemes have been proposed.As we can see from the ID-based cryptosystems，the identity information is very easily obtained from the ciphertexts or signatures.

In some network applications，we have to distribute a same message to several different persons.The concept of multi-receiver setting was formalized by Bellare et al.［3］Zheng［4］proposed a signcryption scheme for multiple recipients.Duan et al.［5］defined the security notion for multi-receiver ID-based signcryption scheme in 2006and also proposed an efficient concrete scheme.But Tan［6］showed that Duan's scheme［5］was not secure against adaptive chosen ciphertext attacks under their security model.In 2007，Yu et al.［7］proposed a new identity based signcryption scheme for multiple receivers.However，Selvi et al.［8］showed that Yu et al.'s scheme［7］did not satisfy the unforgeability and proposed an improved scheme.Li et al.［9］pointed out that neither Yu et al.'s scheme［7］nor Selvi et al.'s scheme［8］satisfied the confidentiality.In 2009，Selvi et al.［10］presented a new scheme and in 2011，Ming et al.［11］proposed a concrete scheme secure in the standard model.

For protecting the privacy of receivers，in many situations，an authorized receiver does not want to reveal its identity to any other receivers，except the sender.Receiver anonymity or privacy protection means that one can examine whether herself／himself is one of the selected receivers，and nobody in the receiver set knows who the other selected receivers are.For example，in paid-TV systems the privileged set is the set of all users who have paid a subscription to a certain channel.Each customer should have access to that channel using his private key.The problem is that，using the traditional solve method，he has to know who else has paid for the specific subscription which causes serious privacy issues.Recently，the study of privacypreserving （or anonymous）schemes has received much attention from cryptographic researchers［12-16］.In 2013，Pang et al.［17］proposed a novel multi-recipient signcryption scheme with complete anonymity（IBMRSCwCA scheme）.The identities of the sender and all of the recipients were kept secret.They claimed the new concrete scheme was strong existential unforgeability under selective multi-ID，chosen message attack（SUF-sMIBSC-CMA）.

In this paper，however，we show that Pang et al.'s scheme is actually insecure.We give two different attacks，named“inside attack”and“outside attack”，respectively，to the concrete scheme.In the following，we first review some hard problems and security assumptions and the algorithm model and security notions of IBMRSCwCA scheme，respectively.And then we give an overview of Pang et al.'s concrete scheme （PLGW Scheme）.Then we present the attacks on it and give our concluding remark.

1 Preliminaries

1.1 Bilinear pairings

Let G1be a cyclic additive group of large prime order q and G2be a cyclic multiplicative group of the same order q.Let P be a generator of G1.A bilinear pairing is a map e：G1×G1→G2and satisfies the following properties：

1）e is bilinear，i.e.，e（aP，bP）＝e（P，P）abfor all a，b ∈；

2）e is non-degenerate，i.e.，e（P，P）≠1G2；

3）e is efficiently computable.

We refer the reader to Ref.［18］for more details on the construction of such pairings.

1.2 Security problems and complexity assumptions

1）Computation Diffie-Hellman（CDH）problem

Given P，aP，bP ∈G1for unknown a，b ∈，compute abp ∈G1.

Definition 1 CDH assumption

Given P，aP，bP ∈G1for unknown a，b ∈，the successful advantage of any probabilistic polynomial time（PPT）adversary Ais presented as AdvCDH＝Pr［A（P，aP，bP）＝abP｜a，b ∈］.We say that the（t，ε）-CDH assumption holds if there exists no PPT adversary A with non-negligible advantageεwithin running time t in solving the CDH problem.

2）Bilinear Diffie-Hellman（BDH）problem

Given P，aP，bP，cP ∈G1for unknown a，b，c ∈，compute e（P，P）abc∈G2.

Definition 2 BDH assumption

Given P，aP，bP，cP ∈G1for unknown a，b，c ∈，the successful advantage of any PPT adversary A is presented as AdvBDH＝ Pr［A（P，aP，bP，cP）＝e（P，P）abc｜a，b，c ∈］.We say that the（t，ε）-BDH assumption holds if there is no PPT adversary A with nonnegligible advantageε within running time t in solving the BDH problem.

3）Decision bilinear Diffie-Hellman（DBDH）problem

Given P，aP，bP，cP ∈G1for unknown a，b，c ∈，and R ∈G2，decide whether e（P，P）abc＝R.Definition 3 DBDH assumption

Given P，aP，bP，cP ∈G1for unknown a，b，c ∈，and R ∈G2，the successful advantage of any PPT adversary Ais presented as

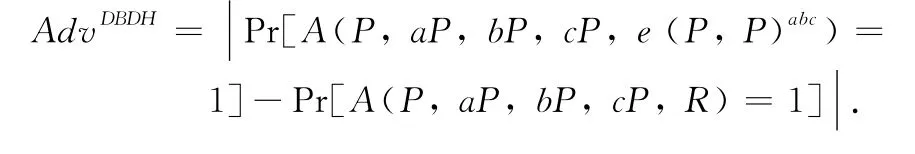
We say that the（t，ε）-DBDH assumption holds if there exists no PPT adversary A with non-negligible advantageε within running time t in solving the DBDH problem.

1.3 Algorithm model

A generic IBMRSCwCA scheme consists of following PPT algorithms.

Setup：given a security parameter l，the PKG generates a master key s and public parameters Params.Params is made public while s is kept secret.

Extract：given an identity IDuthe PKG runs this algorithm Extract（s，Params，IDu）to generate the private key duassociated with IDuand transmits it to the user via a secure channel.

Anony-Signcrypt：to send a message m to multiple receivers chosen by the signer with identitiesthe signer with identity IDsruns this algorithmAnony-Signcrypt（m，Params，ds，R）to generate a signcrypted ciphertext C.

De-Signcrypt：upon receiving the signer's identity IDsand the ciphertext C，the receiver with identity IDjin the receiver listruns this algorithm De-Signcrypt（C，IDs，dj）and obtains the message m or the symbol⊥indicating that the ciphertext is invalid.

For consistency， we require that if C ＝Anony-Signcrypt（m， Params， ds， R），then m ＝De-Signcrypt（C，IDs，dj）for all 1≤j≤n.

Note that this definition no longer requires the set R as an input to the De-Signcrypt algorithm.This is crucial in developing the notion of anonymous multi-receiver signcryption，for which we next provide an appropriate security model for the case of selective adversaries.

1.4 Security notions

In Ref.［17］，Pang et al.formalized several security notions for a generic IBMRSCwCA scheme.Since our attacks presented in this paper are against the unforgeability of their scheme，we here only review this security notion.

The security notion of strong existential unforgeability under selective multi-ID，chosen message attack （SUF-sMIBSC-CMA）can be defined by the following game between a forger F and a challenger B.

Setup：B runs this algorithm to generate a master key s and a public parameter Params.B gives the Params to F and keeps s secret.Upon receiving this parameter，F outputs n target identities R＊＝.

Queries：F performs a number of queries to B as follows.

1）Extraction query

Upon receiving private key extraction query about an identity ID andB runs the Extract algorithm to get d ＝Extract（s，Params，ID）.

2）Anony-Signcryption query

F chooses a target plaintext M，a list of recipients'identity informationand gives them to B.B randomly chooses an identity IDs，computes the private key ds，generates the ciphertext Anony-Signcrypt（m，Params，ds，R）and returns it to A.

3）De-Signcryption queryand a ciphertext C.B randomly chooses an identity IDj∈Land computes its private key dj.If Cis a valid ciphertext，B decrypts it to obtain the corresponding plaintext M ＝De-Signcrypt（C，Params，dj）and returns it to F；otherwise，B outputs an error message.

Forgery：F finally outputs a new ciphertext message C＊，a list of recipient identitiesIf C＊is the ciphertext of the message M generated by，and can be decrypted by any of recipients in L，C＊is a valid ciphertext and F wins this game.The restriction here is that F cannot ask for private key extraction on IDiand C＊cannot be produced by the Anony-Signcrypt algorithm.

The scheme is said to be（t，ε）-SUF-sMIBSC-CMA secure，if for any SUF-sMIBSC-CMA attacker F，its guessing advantage is less thanεwithin polynomial running time t.

2 Review of PLGW Scheme

PLGW scheme［17］is specified by the following algorithms.

Setup：PKG performs the following process.

1） Let G1be an additive group and G2be a multiplicative group with the same prime order q，（q≥2l，l is a long integer），and let Pbe a generator of G1.Choose a bilinear mapping e：G1×G1→G2.

2）Define four one-way hash functions：is the length of the plaintext message.

Extract：with Params，s and an identity IDas input，PKG performs this algorithm to generate the private key of the identity ID：

1）compute public key QID＝H1（ID）；

2）compute private key dID＝s·H1（ID）＝s·QID.

Anony-Signcrypt：with Params，aplaintext M and the private key dsas input，the signer IDschooses a list of recipients'identityand performs this algorithm to generate the ciphertext C of the plaintext M：

1）randomly choose two integers r，α ∈and an element P1∈G1，and then compute Y ＝rQs，U ＝αP，X＝αY，ω ＝e（Ppub，P1）α，andσ＝H2（ω）⊕M，where Qsis the public key of IDs；

2）for i＝1，2，…，n，compute xi＝H3（IDi）and yi＝α（P1＋Qi），where Qiis the public key of IDi；

5）compute h ＝H4（σ，X，U，T）and W ＝（α＋h）·rds，where dsis the private key of IDs；

6）generate the ciphertext：C ＝〈Y，X，U，σ，W，T〉.

De-Signcrypt：with C ＝ 〈Y，X，U，σ，W，T〉，Params，the recipient's identity IDiand the private key dias input，the recipient IDidecrypts Cas follows.

1）Public verification

The one，who has not registered to PKG，can use the following steps to check the integrity or validity of the ciphertext.The registered participant can skip this process and directly jump to the following judgement algorithm：

（1）compute h ＝H4（σ，X，U，T）；

（2）verify whether the equation e（W，P）＝e（X ＋hY，Ppub）holds；if yes，the ciphertext is valid；otherwise，the ciphertext is invalid or has been damaged during transmission.

2）Judgement

The one，who has registered to PKG，can use the following steps to check whether the ciphertext is valid and whether he is an authorized recipient before the following encryption process：

（1）compute h ＝H4（σ，X，U，T）；

（2）check whether the equation e（W，Qi）＝e（X ＋hY，di）holds；if yes，it means that IDiis one of the recipients designated by the signer and the ciphertext is valid；otherwise，the recipient quits the decryption process.

3）De-Signcryption

The authorized user can recover the plaintext by the following steps：

（1）compute xi＝H4（IDi）and the computeηi＝T1＋xiT2＋…＋（）Tn.

（2）computeω′＝e（Ppub，ηi）e（U，di）-1and then get the plaintext as M′＝σ ⊕H2（ω′）.

3 Cryptanalysis of PLGW Scheme

3.1 Inside attack

PLGW scheme is claimed to be strong existential unforgeability under selective multi-ID，chosen message attack.Here we indicate that the ciphertext can not be distinguished under any authenticated identity.It means that a certain ciphertext can be generated by any user who has a valid private key.

Without loss of generality，we assume there are two signers A and B with the private key dA＝s·H1（IDA）＝s·QIDAand dB＝s·H1（IDB）＝s·QIDBrespectively.

With Params，aplaintext M and the private key dAas input，the signer A runs the Anony-Signcrypt algorithm and generates a ciphertext CA＝＜YA，XA，UA，σA，WA，TA＞.In this algorithm，A picks some random elements including rA，αA，P1Aand the following equalities hold：Y＝rAQA，UA＝αAP，X ＝αAY，ωA＝e（Ppub，P1A）αAand σA＝H2（ωA）⊕M.For i＝1，2，…，n，xi＝H3（IDi），yiA＝αA（P1A＋Qi），hA＝H4（σA，XA，UA，TA）and WA＝（αA＋hA）·rdA.

In the following，it is shown that there are random elements including rB，αB，P1B，by which B can produce the same signcryption ciphertext.

If B chooses random elements rB＝；αB＝αA；P1B＝P1A.Then B could produce the signcryption ciphertext as follows：

1）compute Y ＝rBQB，U ＝αBP，X ＝αBY，ω ＝，andσ ＝H2（ω）⊕M；

2）for i＝1，2，…，n，compute xi＝H3（IDi），yi＝αB（P1B＋Qi）；

5）compute h ＝H4（σ，X，U，T），and then compute W ＝（αB＋h）·rBdB；

6）generate the ciphertext：C ＝〈Y，X，U，σ，W，T〉.

Obviously，the signcryption ciphertext generated by B is the same as that generated by A.In other words，given C ＝〈Y，X，U，σ，W，T〉on the message M，it could be generated by any user with a valid private key.So，in Pang et al.'s security model，the target identity R＊＝（，，…，）is meaningless.Any ciphertext could be regarded as the valid forged ciphertext generated by，i∈｛1，2，…，n｝.

It could be viewed as an inside attack made by any valid user who had a private key.

3.2 Outside attack

In the following we will show a more dangerous forgery which can be made by any user.Given the public parameters Params＝〈G1，G2，q，e，P，Ppub，H1，H2，H3，H4〉，even an outside attacker A who don't has a valid private key can generate a valid ciphertext as follows：

1）randomly choose three integers r′，r，α ∈and compute d＝r′·Ppub；then randomly choose a element P1∈G1and compute Y ＝r·r′·P，U ＝αP，X ＝αY，ω ＝e（Ppub，P1）α，andσ ＝H2（ω）⊕M；

2）for i＝1，2，…，n，compute xi＝H3（IDi），yi＝α（P1＋Qi）；

5）compute h ＝H4（σ，X，U，T），and then compute W ＝（α＋h）·r·d ＝（α＋h）·r·r′·Ppub；

6）generate the ciphertext：C ＝〈Y，X，U，σ，W，T〉.

Now we will prove that the tuple C is a valid signcryption ciphertext.

Since

the result of public verification algorithm is correct.

For each authorized IDiwith a private key di，wherei

So the tuple is regarded as a valid ciphertext.

After the receiver computesηi＝T1＋xiT2＋… ＋Tn，he can compute

Now he can successfully recover the message since the tuple Cis a completely valid signcryption ciphertext which is forged by an attacker without any secret information but only the public parameters.

4 Conclusions

Anonymity is a very important security objective in network communications.IBMRSCwCA scheme can achieve both the signers'and the recipients'anonymity at the same time.In the security model，the ciphertext cannot be distinguished under different identities.But on one hand，as we can see from the notion of strong existential unforgeability under selective multi-ID，chosen message attack in the PLGW scheme，it is required to distinguish the ciphertext under the selective multi-ID in order to determine the success of forgery.So the notion is not suitable.On the other hand，the randomization of the users'identities make the outside attacker could generate a “valid”private key without any secret information but only the public parameters.We have proved the vulnerability of the scheme with the security notion for signcryption schemes.We leave it as an open problem to construct an IBMRSCwCA scheme with provable security.

［1］Shamir A.Identity-Based Cryptosystem and Signature Scheme［C］.Proceeding of the CRYPTO 1984，Santa Barbara，USA，1985：120-126.

［2］Malone-Lee J.Identity Based Signcryption［EB／OL］.（2002-07-19）［2014-05］.http：／／eprint.iacr.org／2002／098.

［3］Bellare M，Boldyreva A，Micali S.Public-Key Encryption in a Multiuser Setting：Security Proofs and Improvements［C］.Proceeding of the EUROCRYPT 2000，Bruges，Belgium，2000：259-274.

［4］Zheng Y L.Signcryption and Its Applications in Efficient Public Key Solutions ［C］.Proceeding of the ISW 1997，Tatsunokuchi，Ishikawa，Japan，1998：291-312.

［5］Duan S S，Cao Z F.Efficient and Provably Secure Multireceiver Identity-Based Signcryption［C］.Proceeding of the ACISP 2006，Melbourne，Australia，2006：195-206.

［6］Tan C.On the Security of Provably Secure Multi-receiver IDBased Signcryption Scheme ［J］.IEICE Transactions on Fundamentals of Electronics，Communications and Computer，2008，91（7）：1836-1838.

［7］Yu Y，Yang B，Huang X Y，et al.Efficient Identity-based Signcryption Scheme for Multiple Receivers［C］.Proceeding of the ATC 2007，Hong Kong，China，2007：13-21.

［8］Selvi S S D，Vivek S S，Gopalakrishnan R，et al.Cryptanalysis of ID-Based Signcryption Scheme for Multiple Receivers［EB／OL］.（2009-05-26）［2014-05］.http：／／eprint.iacr.org／2009／238.

［9］Li F，Hu X，Nie X Y.A New Multi-receiver ID-Based Signcryption Scheme for Group Communications ［C］.Proceeding of the ICCCAS 2009，Milpitas，California，USA，2009：296-300.

［10］Selvi S S D，Vivek S S，Srinivasan R，et al.An Efficient Identity-Based Signcryption Scheme for Multiple Receivers［C］.Proceeding of the IWSEC 2009，Toyama，Japan，2009：71-88.

［11］Ming Y，Zhao X M，Wang Y M.Multi-receiver Identity-Based Signcryption Scheme in the Standard Model ［C］.Proceeding of the ICICA 2011，Qinhuangdao，China，2011：487-494.

［12］Pang L J，Cui J J，Li H X，et al.A New Multi-receiver IDBased Anonymous Signcryption ［J］.Chinese Journal of Computer，2011，34（11）：2104-2113.（in Chinese）

［13］Lal S，Kushwah P.Anonymous ID Based Signcryption Scheme for Multiple Receivers［EB／OL］.（2009-07-12）［2014-05］.http：／／eprint.iacr.org／2009／345.

［14］Zhang B，Xu Q L.An ID-Based Anonymous Signcryption Scheme for Multiple Receivers Secure in the Standard Model［C］.Proceeding of the AST／UCMA／ISA／ACN Conferences，Miyazaki，Japan，2010：15-27.

［15］Zhang J H，Gao S N，Chen H，et al.A Novel ID-Based Anonymous Signcryption Scheme ［C］.Proceeding of the Advances in Data and Web Management Joint International Conferences，Suzhou，China，2009：604-610.

［16］Huang X Y，Susilo W，Mu Y，et al.Identity Based Ring Signcryption Scheme：Cryptographic Primitive for Preserving Privacy and Authenticity in the Ubiquitous World ［C］.Proceeding of the 19th International Conference on Advanced Information Networking and Applications，Taipei，China，2005：649-654.

［17］Pang L J，Li H X，Gao L，et al.Completely Anonymous Multi-recipient Signcryption Scheme with Public Verification［J］.PLOS ONE，2013，8（5）：e63562.

［18］Boneh D，Franklin M.Identity-Based Encryption from the Weil Pairing［C］.Proceeding of the CRYPTO 2001，Santa Barbara，USA，2001：213-229.