基于位置演进模型的两类时空查询算法
刘 林,刘 磊,熊小鹏
(1.重庆邮电大学 计算机科学与技术学院,重庆400065;2.中国移动通信集团河南有限公司洛阳分公司,河南 洛阳471000;3.中国移动通信集团重庆有限公司,重庆401121)
0 引 言
智能交通、数字战场、疾病传播研究等领域的新型应用依赖于物体历史位置的采集、存储、索引与查询。位置采集中,移动对象依靠通讯基站、GPS、北斗信号等方式获取自身位置,通过GPRS、TCP/IP、WLAN 等网络传输协议向时空数据库提交位置信息。受耗电量、网络带宽与数据库性能限制,位置信息传输通常按预设规则间隔触发,例如距上次采集超过预设时间阀值 (如60s)或距离阀值(如500m)。时空数据库记录对象在离散时间点上对应位置坐标,对于这些时间点外任意时刻,前期多数研究假定对象位置保持静止,该模型称为位置跳跃模型 (location hop model,LHM)。
本文针对两类时空查询,即历史时间窗范围查询与历史时间窗近邻查询,分析LHM 下存在的查询结果偏差问题,提出位置演进模型 (location evolution model,LEM)与该模型中上述两类时空查询处理的理论算法。针对现实环境条件与效率要求,文中进一步给出按匀速直线运动简化的位置演进模型(LEM_uniform linear,LEM_UL)与对应查询处理算法。本文提出的位置演进模型与两类时空查询处理算法,可有效消除并降低位置跳跃模型下的查询偏差。
1 背景分析
根据查询维度差异,时空查询具有不同类别划分。例如:①根据查询时段分为历史信息查询[1,2]、当前信息查询与未来预测查询[3-5];②根据条件时长分为时间窗查询与时间片查询[2-6];③根据空间条件分为范围查询、多种近邻查询、逆近邻查询、Reachability查询等等[6-12];④根据查询区域/点可否移动,分为静止查询与移动查询[10-14];⑤存在更多类别划分方式。其中范围查询与近邻查询是多种衍生查询的基础,具有重要研究价值。结合位置采集与传输技术臻于成熟的现状,本文研究两类具备实用前景的基础查询:历史时间窗范围查询(historical time-window range query,HTWRQ)与历史时间窗近邻查询(historical time-window k-nearest-neighbor query,HTWkNNQ)。
1.1 历史时间窗范围查询 (HTWRQ)
HTWRQ:假定目标对象总数为N。已知对象标志集O= {o1,o2,…,oN},与对象位置函数集L= {l1(t),l2(t),…,lN(t)},其中l(t)为对应o随时间变化的位置函数。根据给定查询历史时段W 与查询区域R,求W 时段内位于R 内的对象集。
输出结果Result= (<W1,O1>,<W2,O2>,…,<WS,OS>),其中:
(1)S 为正整数;
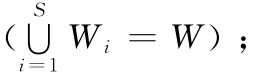
(3)Oi代表Wi时段内位于R 内的对象标志集,OiO;对ia=ib-1,满足Oia≠Oib。
1.2 历史时间窗近邻查询 (HTWkNNQ)
HTWkNNQ:同HTWRQ,已知对象标志集O 与对象位置函数集L。根据给定查询历史时段W 与查询中心点H,求W 时段内距离H 最近的k个对象。
输出结果Result= (<W1,O1>,<W2,O2>,…,<WS,OS>),其中:
(1)S 为正整数;
(2)Wi代表W 内子时段,当1≤ia<ib≤S,满足(Wia早于Wib)且(Wia∩Wib=Φ)且(∪S
i=1Wi=W);(3)Oi代表Wi时段内距离H 最近的k 个对象标志所组成的有序集合,OiO;对ia=ib-1,满足Oia≠Oib(即Oia与Oib元素或元素排序不完全一致)。
针对HTWRQ 与HTWkNNQ 在内的各种时空查询,前期研究多基于以下模型进行处理,本文将其定义为位置跳跃模型。
1.3 位置跳跃模型LHM
假设对象o的位置更新时刻为 (t1,t2,…,tm),对应所更新位置为 (u1,u2,…,um)。则对任意时刻t∈[ti-1,ti),o的位置由函数l(t)=ui-1计算 (其中i,m∈N+,i≤m)。图1对LHM 进行说明,对象o在 {ti、ti+1、ti+2}时刻更新位置为 {ui、ui+1、ui+2}。易见更新时间点外任意时刻,单实曲线代表的对象实际位置与双实直线代表的对象计算位置存在位置偏差。该位置偏差可导致3类查询结果偏差。
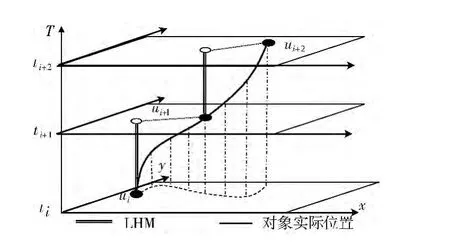
图1 位置跳跃模型位置偏差
1.3.1 结果遗漏
图2描述一个已知O、L、R 与W = [t,t+60s]的HTWRQ。虚线代表某对象A 实际轨迹。W 时段内,A 的位置信息在a1、a3、a5处更新。A 在位置a2与a4分别进入与离开R。a1~a5对应时间点分别为t1~t5。

图2 HTWRQ 示例
直观易见本查询正确结果为< [t2,t4),{A}>。而LHM 模型下查询结果为< [t3,t5), {A}>。注意A 在[t2,t3)时段LHM 计算位置始终为a1。因a1处于R 外,该时段A 不在LHM 查询结果中。然而该时段A 实际位于R 内。因此LHM 模型导致该查询在 [t2,t3)时段结果遗漏。
1.3.2 结果超出
接上例。A 在时段 (t4,t5)LHM 计算位置始终为a3。因a3在R 内,A 在该时段LHM 查询结果中。而该时段A实际位于R 外,LHM 模型导致该查询在 (t4,t5)时段结果超出。
1.3.3 结果错误
图3描述一个已知O、L、H、W = [t,t+60s]、k=1的HTWkNNQ。有向线段代表对象A 与B 的实际轨迹。时刻t-10s、t+40s对象A 更新位置信息至at-10、at+40;时刻t-10s、t+50s对象B更新位置信息至bt-10、bt+50。
选取 (t+20s,t+40s)子时段进行分析,LHM 下A与B位置信息值分别为at-10、bt-10,距离比较为B<A,则该子时段查询结果为{B}。而该子时段A 实际位置较B 实际位置更邻近H。因此LHM 模型导致该子时段内查询结果错误。
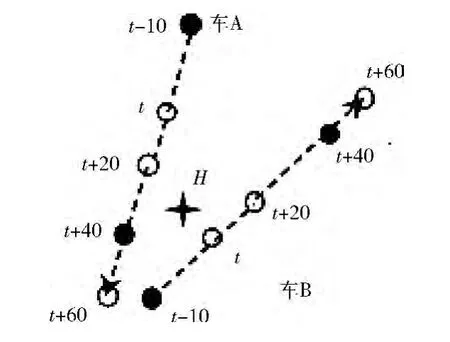
图3 HTWkNNQ 示例
2 位置演进模型时空查询算法
针对LHM 下查询结果偏差问题,本章提出位置演进模型LEM,并给出该模型下HTWRQ 与HTWkNNQ 理论算法。
2.1 位置演进模型LEM
轨迹函数:依据对象实际运动轨迹,描述对象位置随时间连续变化的函数。对象o在D 维空间中的轨迹函数表示为
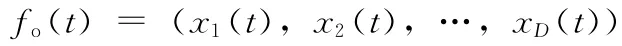
其中xi(t)(其中i= {1,…,D})表示o在第i维空间位置随时间t的运动变化。在任意时刻,fo(t)的值与o实际所在位置一致。
位置演进模型LEM:每个移动对象o在历史时段 [ts,te]的轨迹函数fo(t)已知。对任意时刻t∈ [ts,te],o的位置由函数l(t)=fo(t)计算。
相较位置跳跃模型,位置演进模型LEM 最重要的特性是任何对象在任意时刻的位置可通过其轨迹函数被准确计算。该特性也意味着即使历史对象未进行显式的位置更新,也能根据轨迹函数持续进行隐式位置变更。LEM 一方面从根本上消除对象计算位置与实际位置的偏差,进而消除查询结果偏差;另一方面对时空查询算法提出新要求以支持对象位置隐式、持续的变更。
本章假设所有对象的轨迹函数已知。轨迹函数的求取存在多种计算方法不在本文讨论范围。第3节中给出一种高效实用的轨迹函数近似方法与查询处理算法。
2.2 基于LEM 的历史时间窗范围查询
算法思想:查询时段内,单个移动对象轨迹与查询区域R 边界存在零个、一个或多个相交时刻。求得所有对象的所有相交时刻并升序排列,形成查询边界交点时刻集C。由交点间单一关系定律1,当且仅当在C 中各交点时刻发生对象进入或离开查询区域。则C 中各时刻在查询时段内产生的若干子时段,正是查询结果子时段Wi。根据对象轨迹函数求得各Wi子时段对应的结果对象标识集Oi。
交点间单一关系定律1 对于D 维空间中单连通区域P与连续曲线Q,若P 与Q 边界存在x 个交点将Q 切分为x+1条曲线段,则任一曲线段上所有点 (除交点外)或全在P内,或全在P外。该定律易通过反证法求得证明,此处不赘述。
基于LEM 的历史时间窗范围查询算法:
输入:
对象标识集O= {o1,o2,…oN}
对象位置函数集L= {l1(t),l2(t),…lN(t)}
查询历史时段W = [ts,te]
查询区域R
输出:
Result= (<W1,O1>,<W2,O2>,…<WS,OS>),其中S、Wi、Oi同第1节中HTWRQ 定义
算法过程:
(1)查询边界交点时刻集C=null;Result=null;
(2)对每个对象oi∈O
1)求函数li(t)与R 的交点时刻集Ci
2)Ci中排除掉大于ts或小于te的时刻
3)若Ci≠null或li((ts+te)/2)属于R
C=C∪Ci
标记oi为结果对象成员;
(3)C=C∪ {ts,te},去重,并升序排列成有序集合;
(4)for i=1to|C|-1
1)Wk= [C [i],C [i+1]),Oi=null;
2)对每个结果对象成员o
若li((C [i]+C [i+1])/2)属于R
Oi=Oi∪ {o};
3)Result=Result+<Wi,Oi>;
(5)返回Result;
算法步骤 (2)中1)通过各个对象轨迹函数,求每个对象在查询时段内与查询边界的相交时刻。若查询时段内有交点时刻存在,则该对象在结果集中至少出现一次,步骤 (2)中3)标记该对象为结果对象成员。若查询时段内无交点存在,步骤 (2)中3)利用交点间单一关系定律1,检测当前对象在查询时段中间时刻位置,判断是否是对象在整个W 时段处于区域R 内的特殊情况。步骤 (2)同时获得查询边界交点时刻集C。将C 升序排列后,步骤 (4)通过检测子时段中间时刻,判断当前对象是否属于该子时段结果集,从而求取该时段内位于查询区域内的对象集合。
2.3 基于LEM 的历史时间窗近邻查询
不同于HTWRQ 只需独立考察单个对象与查询区域R的位置关系,HTWkNNQ 需跟踪各对象与查询中心点H的距离变化,并根据距离远近对各对象排序。LEM 下各对象位置随时间持续变化,因此HTWkNNQ 查询算法的核心在于确定各对象距中心点距离排序产生变化的时刻。
2.3.1 中心点距离函数
单个对象距中心点的距离随时间变化的函数。已知对象o的轨迹函fo(t)= (x1(t),x2(t),…,xD(t)) (如2.1节所定义),中心点H 的位置坐标H= (h1,h2,…,hD),则o与H 的中心点距离函数do,H(t)表示为
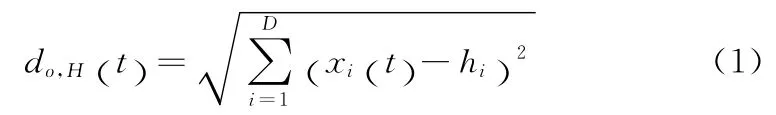
2.3.2 算法思想
对每个对象,通过其轨迹函数求得中心点距离函数,并求解任意2个对象距中心点距离相同的时刻集。合并以上时刻集,去重并按升序排序,形成距离函数相交时刻集C。根据下述交点间单一关系定律2及推论1,当且仅当在C 中各交点时刻k 最近邻有序对象集合发生变化,则C 中各时刻在查询时段内产生的若干子时段,正是查询结果子时段Wi。根据各对象中心点距离函数,求得各Wi子时段距离中心点最近的k 个对象标识集Oi。
交点间单一关系定律2 对于D 维空间中相同定义域内的2个连续函数f1(t)、f2(t),若解集 {t|f1(t)=f2(t)}存在,设该解集为 {t1,t2,…,tx} (t1<t2<…<tx),那么对于任意t∈(tk,tk+1)(k∈ {1,…,x-1}),对于同一个k,f1(t)始终大于f2(t)或始终小于f2(t)。
推论1 已 知 连 续 函 数 集 合F(t)= {f1(t),f2(t),…fm(t)},求解F(t)中所有函数两两之间解集 {t|fi(t)=fj(t),i≠j且i、j∈ {1,…,m}},以上解集的并集记为 {t1,t2,…,ty}(t1<t2<…<ty),则对于开区域 (tk,tk+1)(k∈ {1,…,y-1})与固定k,F(t)内所有函数值的大小关系在该区域内保持不变。以上定律及推论均容易通过反证法证明,此处不赘述。
基于LEM 的历史时间窗时空近邻查询算法:
输入:
对象标识集O= {o1,o2,…oN}
对象位置函数集L= {l1(t),l2(t),…lN(t)}
查询中心点H= (h1,h2,…,hD)
最近邻个数值k
查询历史时段W = [ts,te]
输出:
Result= {<W1,O1>,<W2,O2>,…<WS,OS>},其中S、Wi、Oi同第1节中HTWkNNQ 定义
算法过程:
(1)距离函数相交时刻集C=null;
中心点距离函数集DisSet=null;Result=null;
(2)对每个对象oi∈O
1)根据式 (1)得到中心点距离函数dOi,H()t ;
2)DisSet=DisSet∪ (dOi,H(t) );
(3)for i=1to|DisSet|-1,
for j=i+1to|DisSet|
1)求解DisSet[i]=DisSet [j] (其中t定义域为W),其解集记为C(i,j);
2)C=C∪C (i,j);
(4)C=C∪ {ts,te},去重,并升序排列成有序集合;
(5)for i=1to|C|-1;
1)Wi= (C [i],C [i+1]],Oi=null;
2)计算DisSet((C [i]+C [i+1])/2))并升 序排序;
//DisSet(tx)代表DisSet中各函数在tx值的集合;
3)Oi=DisSet((C [i]+C [i+1])/2))中前k个值对应对象;
4)Result=Result∪ {<Wi,Oi>};
(6)返回Result;
步骤 (2)通过式 (1)得到查询时段内每个对象与查询中心点间距离函数,记入集合DisSet;步骤 (3)对Dis-Set中所有距离函数两两等式计算,求解任意两函数在查询时段W 内的交点时刻集C(i,j),合并至距离函数相交时刻集C;去重并升序排序C 后,步骤 (5)对每个结果子时段求取该时段内距离中心点H 最近的k 个对象的有序集合。其中步骤 (5)中2)计算各对象在每个子时段内中间时刻距H 的距离,并升序排列。利用交点间单一关系定律2及推论1,该顺序在相应子时段内不会改变。因此步骤(5)中3)取步骤 (5)中2)所得集合中前k 个对象作为相应子时段结果对象集。
注意步骤 (5)的1)中取Wi为前开后闭区间。由于在步骤 (5)的3)中,在子时段端点时刻上,序位第k 的对象可能与后续一个或多个相邻对象距中心点的距离相同。该情况下,本算法保持子时段内既有结果对象作为端点时刻结果。
3 基于LEM_UL的时空查询
本章节将说明LEM 时空查询面临的挑战。针对这些挑战,本文采用移动对象在相邻位置更新时刻间做匀速直线运动思想,求解移动对象近似轨迹函数,建立匀速直线位置演进模型LEM _UL;同时伴随查询区域边界函数、中心近似距离函数的获取,实现相应基于LHM 的时空查询向基于LEM_UL的时空查询转化。
由于基于LEM_UL 的历史时间窗范围查询、近邻查询算法与基于LEM 的相应查询算法的算法思想、输入输出形式、算法中使用变量的描述基本相同,因此算法过程将不再赘述。
3.1 基于LEM 时空查询面临的挑战
LEM 时空查询从理论上能够消除LHM 时空查询存在的结果偏差问题,但在实际时空查询应用中存在以下挑战:
(1)由于移动对象在位置采集时刻外任意时刻的位置信息缺失,因此移动对象真实的轨迹函数难以获取,使LEM 的建立无法实现。进而致使基于LHM 的时空查询难以向相应基于LEM 的时空查询转化。
(2)目前研究中存在多种合成移动对象轨迹函数的方法,例如高阶插值[15],但合成函数具有高阶性质且形式复杂,使算法效率难满足高实时要求的应用。
3.2 移动对象近似轨迹函数及LEM_UL定义
本文通过假设移动对象在其相邻位置更新时刻间做匀速直线运动求得对象的轨迹函数,称为移动对象近邻轨迹函数。另外,为使章节内容更易理解,本节针对二维空间中移动对象近似轨迹函数进行求解。
3.2.1 移动对象近似轨迹函数
二维空间中,已知移动对象o在相邻位置更新时刻ti、ti+1下 的 记 录 为ui(oid,xi,yi,ti)、ui+1(oid,xi+1,yi+1,ti+1),则对象o在 [ti,ti+1]时段内的轨迹函数fo(t)为
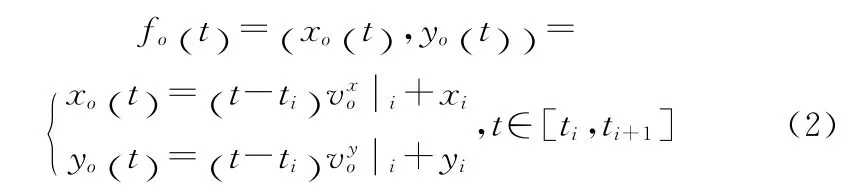
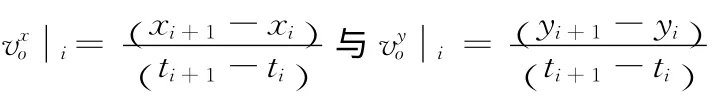
由于本章节时空范围算法涉及查询时段W 内对象轨迹函数,因此需求解该时段内的轨迹函数。已知对象o的位置更新集合为 {u1,…,un}(t1<…<tn),求解W 内轨迹函数首先需从该集合中获取满足ti≤ts<ti+1、tj-1≤te<tj的子集 {ui,…uj},然后使用式 (2)求解o 在 [ti,tj]内的近似轨迹函数,进而求解查询时段W 内对象o的近似轨迹函数
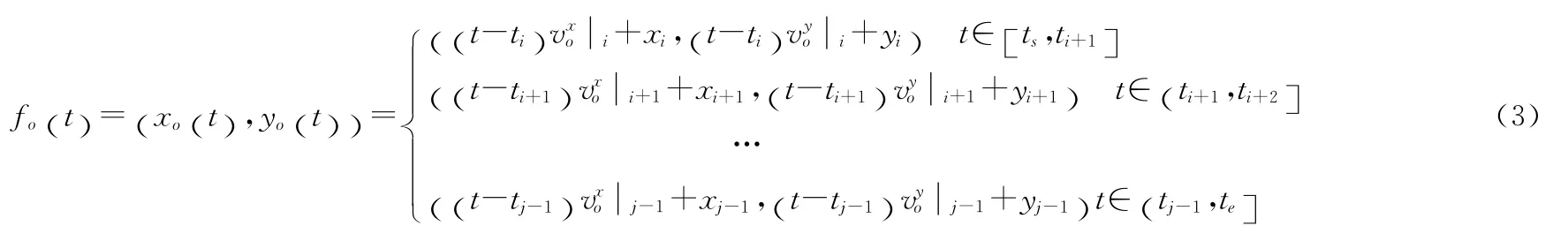
3.2.2 位置匀速直线演进模型LEM_UL
每个移动对象o在历史时段 [ts,te]的轨迹函数fo(t)(如式 (3))已知。对任意时刻t∈ [ts,te],o的位置由函数l(t)=fo(t)计算。
3.3 查询区域及其边界函数
二维空间中时空范围查询的查询区域有多种类型,例如矩形、圆等,本节以矩形查询区域为例给出查询时段内静态查询区域的表示及其边界函数。
本节采用中心点与边长表示矩形,即矩形对角线交点--中心点C(xc,yc),矩形的长和宽分别为2a和2b (a>0,b>0),则矩形顶点坐标分别为:(xc+a,yc+b)、(xc-a,yc+b)、(xc-a,yc-b)和 (xc+a,yc-b)。
查询时段W 内,矩形查询区域R 的中心点为C (xc,yc),R 的长和宽分别为2a、2b。则W 内,查询区域R 表示为
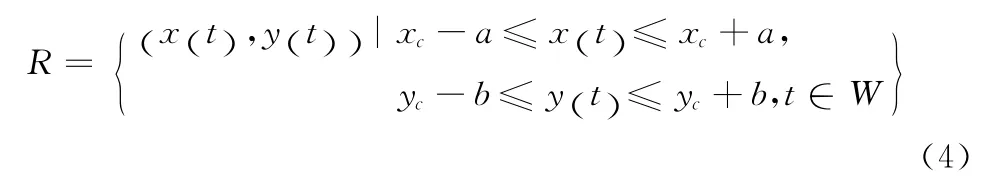
式 (4)说明:对于tx∈W,当且仅当移动对象o的位置坐标 (xo(tx),yo(tx))满足xc-a≤xo(tx)≤xc+a 且yc-b≤yo(tx)≤yc+b时,该对象在tx时刻位于R 内。
查询区域R 的边界由左、右、上、下4条区域边界线段组成,分别为lleft、lright、lup、ldown(如式 (5))。二维空间中,查询时段W 内矩形区域R 的边界函数为
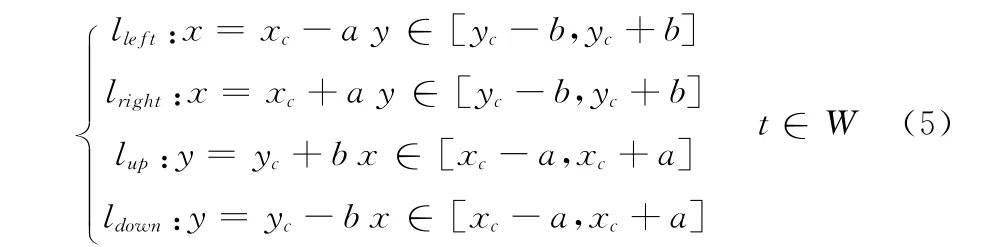
式 (5)说明:当且仅当对象o在tx时刻的位置坐标(xo(tx),yo(tx))满足以下条件之一时,该对象位于查询区域边界上

3.4 中心点近似距离函数
本节通过式 (1)求解查询时段W 内移动对象与查询中心点间的距离函数。但求解中使用移动对象近似轨迹函数 (如式 (3)),因此该距离函数是近似距离函数。
中心点近似距离函数:二维空间中,已知对象o在相邻位 置 更 新 点ui、ui+1间 的 轨 迹 函 数 为fo(t) =((t- ti)voxi+xi, (t- ti)voyi+yi)(由 式 (2)得),查询中心点H 的位置坐标为 (xH,yH)。由式 (1)得,[ti,ti+1]时段内对象o和查询中心点H 的距离函数为
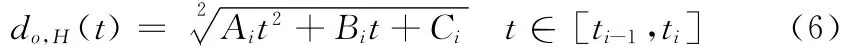
其中Ai= (voxi)2+ ((voyyi))2,Bi=2 [(xi-xH)voxi +(yi-yH)voyi-ti(((voxxi))2+ ((voyyi))2)],Ci=ti2((voxi)2+ ((voyyi))2)+(xi-xH)2+(yi-yH)2。
由于本章节时空最近邻算法涉及查询时段W 内中心点近似距离函数,因此需求解该时段内的距离函数。已知二维空间中,查询时段W 内移动对象o的近似轨迹函数 (如式 (3)),使用式 (6)求得o与H 在W 内的距离函数
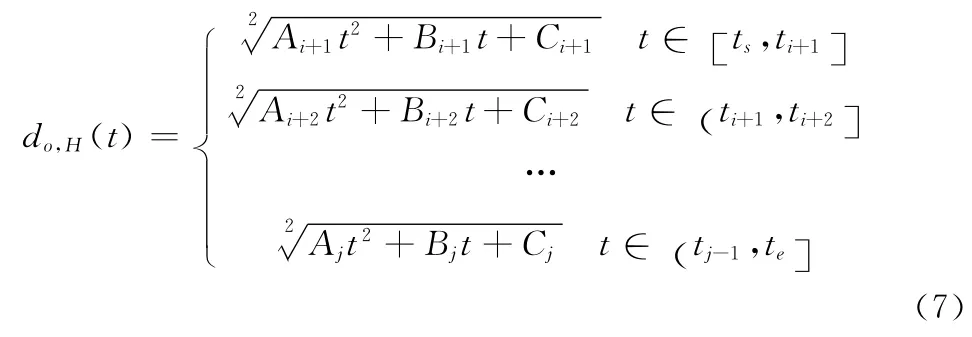
由式 (7)得,二维空间中查询时段W 内移动对象与查 询 中 心 点 的 距 离 函 数 集 为 DisSet ={do1,H(t) ,...doN,H(t) }。
4 实验分析
本节给出基于LEM 时空查询的近似查询定义和基于LHM、LEM_UL的HTWRQ (HTWkNNQ)结果准确度计算方法。并在相同实验环境和准确度计算方法下,通过仿真实验证明基于LEM _UL 的HTWRQ (HTWkNNQ)查询结果准确度普遍比基于LEM 的相应查询结果准确度高。
4.1 基于LEM 时空查询的近似查询
基于LEM 的时空查询依赖移动对象实际轨迹对应的轨迹函数。由于移动对象位置采用离散采集,因此目前针对移动对象实际运动轨迹及其函数的获取方法尚不存在。为描述对象的运动轨迹,多数研究使用人工合成方法获取对象轨迹函数的近似解[15]。本实验通过提高位置采集频率(如每秒或每10m 更新一次)获取对象位置数据集,采用在相邻位置采集点间做匀速直线运动思想获取移动对象轨迹函数的近似解。因此基于该近似解建立的模型的实质为LEM_UL,本实验称基于高位置采集频率上的LEM_UL时空查询是基于LEM 时空查询的近似查询。
4.2 两类查询结果准确度计算方法
基于LHM 的时空查询结果准确度:在相同查询条件下,查询子时段Wi内,基于LHM 的时空查询结果相似度(如式 (8)中ciHTWRQ)同相应时段长度 (时段两端点差的绝对值)积的总和与查询时段W 长度的比值。同理可定义基于LHM 的时空查询结果准确度
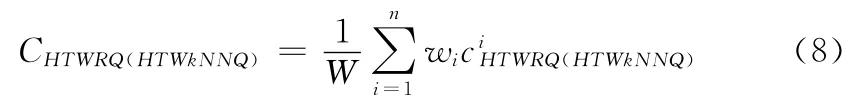
W:查 询 时 段 W,W =w1+w2+ … +wn;CHTWRQ(HTWkNNQ):查询时段W 内,基于LHM、LEM_UL的HTWRQ 或HTWkNNQ 查询结果准确度;ciHTWRQ:wi内基于LHM 或LEM _HL 的HTWRQ 查询结果相似度,即wi内基于LHM 或LEM _UL 的HTWRQ 结果对象集与基于LEM 的HTWRQ 结果对象集中相同对象的个数同后者对象集数的比值;ciHTWkNNQ:wi内基于LHM 或LEM_HL的HTWkNNQ 查询结果相似度,即wi内基于LHM或LEM_UL的HTWkNNQ 结果有序对象集与基于LEM的HTWkNNQ 结果有序对象集中位序且对象相同的个数与k (最近邻数)的比值。
4.3 实验环境
实验使用类似于GSTD 的移动对象数据产生器生成对象的位置更新信息。对于所有对象 (12000个),生成器首先初始化所有对象的初始位置,使对象初始位置信息满足期望为50000 m、方差为10002的正态分布N~ (50000,10002)。在初始位置的基础上,不同对象以10~60s更新周期进行位置更新,每个新的位置都是在其前次位置信息上给予一个更新周期、角度偏值、速度值计算而得。其中,角度偏值在0°~90°、90°~180°、180°~270°、270°~360°之一内满足均匀分布,速度值在1~5m/s、10~15m/s、20~25m/s、30~50m/s之一内满足均匀分布。具体的移动对象集、更新周期、角度偏差范围、速度范围的配置见表1。
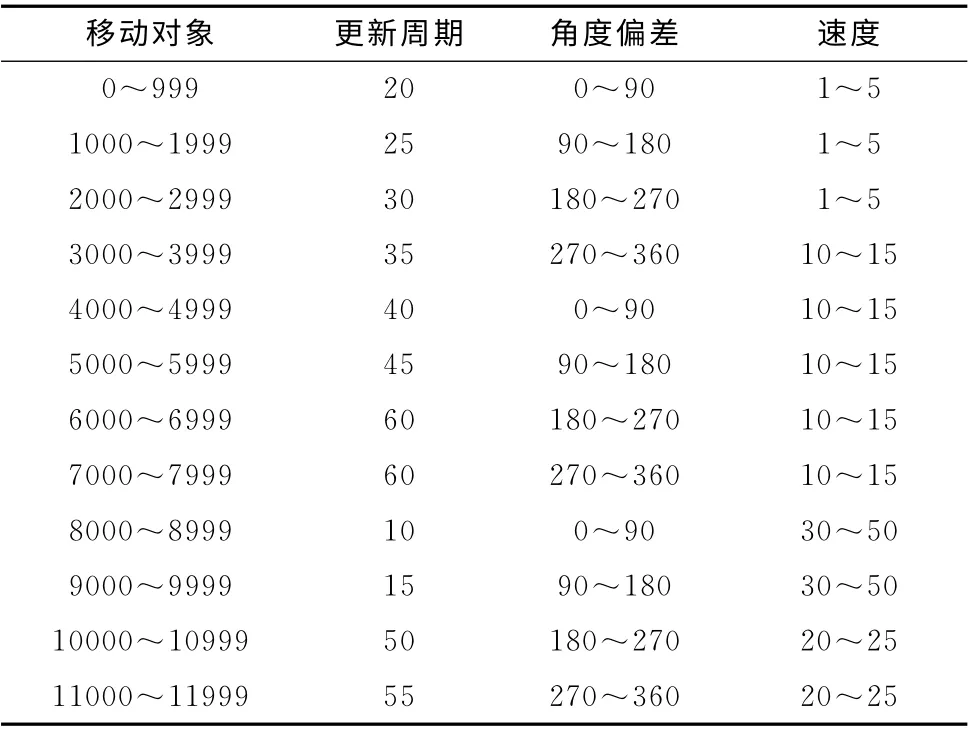
表1 实验环境变量配置
4.4 实验结果
图4、图5分别给出了基于LHM、LEM_UL 的HTWRQ 和HTWkNNQ 查询结果准确度随更新周期的变化曲线。由图4和图5 可知,随着移动对象更新周期的增大,基于上述两类模型的HTWRQ 和HTWkNNQ 查询结果准确度都普遍降低,原因为:对于时间周期位置更新策略,相较于高频繁的位置更新,低频率的位置更新将产生更多位置信息缺失。同一实验环境、查询条件、准确度计算方法下,对于不同更新周期,基于LEM_UL 的HTWRQ 查询结果准确度高于基于LHM 的相应查询结果准确度,如图4所示。
同一实验环境、查询条件、准确度计算方法下,对于不同更新周期,基于LEM _UL 的HTWkNNQ 结果准确度高于基于LHM 的相应查询结果准确度,如图5所示。
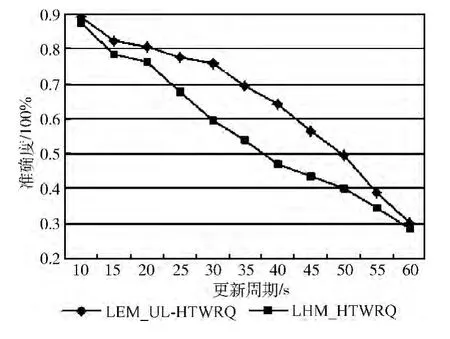
图4 HTWRQ 结果准确度
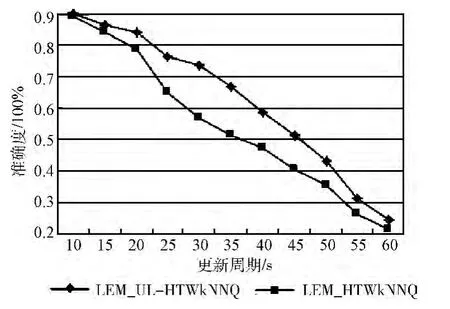
图5 HTWkNNQ 结果准确度
5 结束语
本文举例分析了前期研究中采用LHM 处理历史时间窗时空查询中的结果偏差,提出位置演进模型,从理论上消除基于LHM 的时空查询中的结果偏差。同时,针对实际时空查询应用,提出LEM _UL,给出LEM _UL 历史时间窗范围查询和历史时间窗近邻查询算法。经实验验证,相较于基于LHM 的历史时间窗范围查询和历史时间窗近邻查询算法,相应基于LEM _UL 的相应时空查询算法显著提高了查询结果准确度。
[1]Zheng Kai,Goce Trajecvski,Zhou Xiaofang,et al.Probabilistic range queries for uncertain trajectries on road networks [C]//ACM Proceedings of the 14th International Conference on Extending Database Technology,2011:283-294.
[2]Ralf Hartmut Güting,Thomas Behr,Xu Jianqiu.Efficient k-nearest neighbor search on moving object trajectories[C]//Proceedings of the International Conference on VLDB,2010:687-714.
[3]Stojanovic D,Papadopoulos AN,Predic B,et al.Continuous range monitoring of mobile objects in road networks[J].Data and Knowledge Engineering,2008,64 (1):77-100.
[4]Ugur Demiryurek,Farnoush Banaei-Kashani,Cyrus Shahabi.Efficient continuous nearest neighbor query in spatial networks using Euclidean restriction [C]//Processings of 11th International Symposium SSTD,2009:25-43.
[5]Ahmed M Aly,Walid G Aref,Mourad Ouzzani.Spatial queries with two kNN predicates[C]//Proceedings of the VLDB Endowment,2012:1100-1111.
[6]Yong Hun PARK,Kyoung Soo BDK,Jae Soo YOO.Continuous range query processing over moving objects[J].IEICE Transactions on Information and Systems,2008(11):2727-2730.
[7]Xuan Kefeng,Zhao Geng,David Taniar,et al.Voronoibased range and continuous range query processing in mobile databases[J].Journal of Computer and System Sciences IEEE AIAN,2009,77 (4):637-651.
[8]LI Chun.K-nearest neighbor search on moving object trajectories[D].Hangzhou:Zhejiang University,2007:25-70 (in Chinese).[李春.移动对象轨迹的最近邻居查询研究 [D].杭州:浙江大学,2007:25-70.]
[9]Reynold Cheng,Chen Lei,Chen Jinchuan.Evaluation probability threshold k-nearest-neighbor queries over uncertain data [C]//Proceedings of the 12th International Conference on Extending Database Technology,2009:672-683.
[10]Rimantas Benetis,Christian S Jensen,Gytis Karciauskas,et al.Nearest and reverse nearest neighbor queries for moving objects[C]//Proceedings of the International Conference on VLDB,2006:229-250.
[11]Houtan Shirani-Mehr,Farnoush,Cyrus Shahabi.Efficient reachability query evaluation in large spatiotemporal contact datasets[C]//Proceedings of the International Conference on VLDB Endowment,2012:848-859.
[12]Yildirim H,Chaoji V,Zaki MJ.GRAIL:Scalable reachability index for large graphs[C]//Proceedings of the International Conference on VLDB Endowment,2010:276-284.
[13]Li Chuanwen,Gu Yu,Li Fangfang,et al.Moving k-nearest neighbor query over obstructed regions [C]//IEEE Web Conference(APWEB),2010:29-35.
[14]Yin Xiaolan,Ding Zhiming,Li Jing.Moving continuous k-nearest neighbor queries in spatial network databases [J].Computer Science and Information Engineering,2009,10(4):535-541.
[15]Byunggu Yu,Seon Ho Kim,Thomas Bailey,et al.Curvebased representation of moving object trajectories[C]//Proceedings of the International Database Engineering and Applications Symposium,2004:1098-1105.

