融合IMU 的RGBD-SLAM 算法改进研究
闵华松,杨 杰
(武汉科技大学 冶金自动化与检测技术教育部工程研究中心,湖北 武汉430081)
0 引 言
基于RGB-D传感器的定位技术成为近几年来的热门研究问题。RGB-D 传 感 器 (如Kinect)可 同 时 提 供 彩 色(RGB)和深度 (Depth)图像信息,相比普通相机,连续性好,环境信息更加丰富,因此定位的精度更高,且更容易进行三维地图重建。
基于RGB-D 传感器的定位算法有很多种。如Henry等[1]和Endres 等[2]提 出 的 基 于 图 像 匹 配 技 术 的RGBDSLAM 算法,Kerl等[3]和Audras等[4]提出的基于光度模型的密集特征追踪方法,Stuckler等[5]提出的基于点云匹配技术的方法。本文的定位算法是基于Endres等提出的RGBDSLAM 算法,即采用SIFT/SURF/ORB算法进行特征提取和匹配,然后采用RANSAC算法去除离群点得到初始位姿估计,采用ICP算法进行点云匹配改善位姿估计。由于采用稀疏特征点匹配技术对特征点依赖很大,当特征点数量小于阈值时,匹配会失效;同时由于匹配并非对全部图像信息的匹配,使用RANSAC算法进行运动估计并不能完全代表两帧图像匹配的结果,因此误差必然存在。
对此,一些学者提出使用先验运动估计来提高定位算法的精度和鲁棒性能。如Bouvrie等[6]将IMU 姿态解算值和初始姿态估计进行加权平均融合,得到一个新的姿态估计值,将该值参与到ICP 点云匹配;Hjelmare等[7]将轮式里程计、单轴陀螺仪与视觉里程计进行扩展卡尔曼滤波(EKF),利用运动模型构建预测模型,利用传感器模型构建观测模型;Hervier等[8]则提出基于刚体变换量的Lie群状态方程,以Fisher(费希尔)信息阵描述ICP 算法的协方差,对IMU 与ICP的数据进行了IEKF (广义的扩展卡尔曼滤波)融合。上述方法都在一定程度上提高了RGB-D 定位算法的精度,但是大多都着眼于姿态的融合,常采用轮式里程计测量的速度或者速度常量对位移进行预估,当系统存在漂移或者运动变换量很大时,系统的性能会严重降低。
针对上述问题,本文基于RGBD-SLAM 的定位的算法,提出了如下改进方案:引入IMU 传感器,利用机器人的运动模型、IMU 的测量数据以及测量偏差构建预估模型,采用ICP位姿估计结果构建观测模型,同时将机器人的运动指令和运动限制作为约束条件,进行扩展卡尔曼滤波融合。
1 三轮全向机器人的系统平台和运动模型
1.1 系统平台
本文搭建的实验验证平台为三轮全向移动机器人,其实物图和系统结构图如图1、图2所示。

图1 移动机器人实物
实物图最上层是笔记本,是整个系统的核心处理单元,它接收传感单元检测的环境信息和机器人本体的运动信息,同时控制机器人的运行。中间层是Kinect和九轴惯性传感器razorIMU[9],是系统的传感单元。Kinect每秒可以获取30帧640*480像素的RGB/Depth图像,具有57度的水平视角和43度的垂直视角。razorIMU 具有三轴陀螺仪,三轴加速度计和三轴地磁计,可以检测到的三维坐标系下角速度、线加速度和磁场的实时信息。最底层是全向移动机器人,是整个系统的执行单元。该单元由STM32作主控,具有蓝牙、红外、巡线传感器、夏普红外测距模块、超声波测距模块等外围设备,最大速度为0.6m/s。
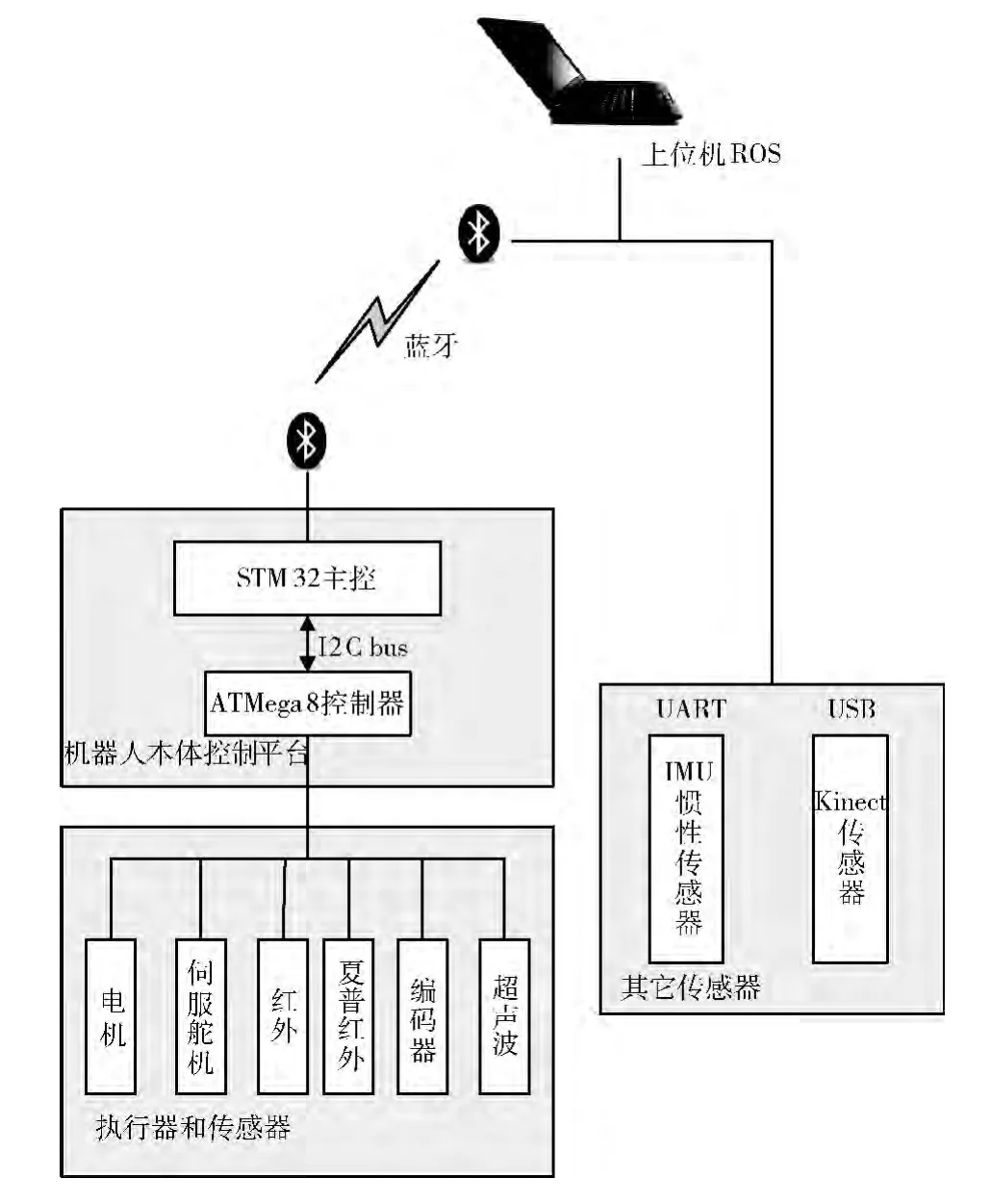
图2 移动机器人系统结构
1.2 三轮全向机器人的运动学方程
三轮全向机器人在平面上可以独立控制机器人对应重心的平移与旋转,并且具有全向移动的优势,能够同时进行旋转和平移运动。其运动学模型如图3所示。
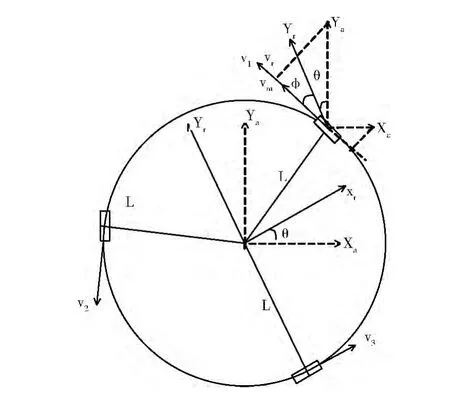
图3 三轮全向轮的运动学模型
其中,全局坐标系为Xa~Ya,机器人坐标系为Xr~Yr,θ为Xa与Xr之间的夹角,为1号轮子与Yr之间的夹角,为30°,L为机器人中心到轮子中心的距离。vi(i=1,2,3)为轮子i沿驱动力方向的速度。
则,三轮全向机器人的运动学方程为
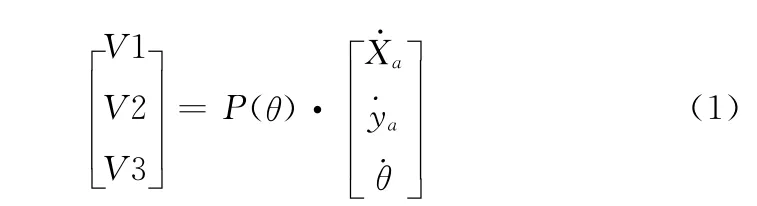
其中
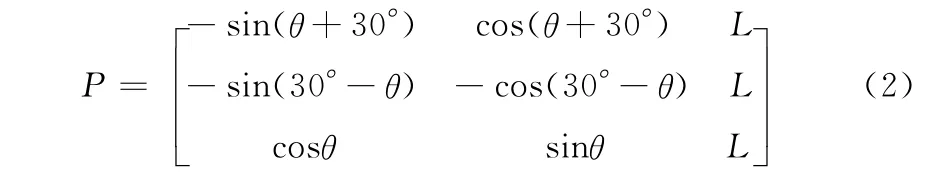
则在给定机器人前进速度和角速度的情况下,可以通过式 (1)求出三轮沿驱动力方向的速度,进而计算三轮的驱动力,驱使电机的运行。对式 (1)求逆运算,可以在已知三轮速度的情况下,求出机器人的前进速度和角速度,这也是轮式里程计的原理。本文中机器人运行过程中存在漂移现象,故舍弃轮式里程计,采用惯性传感器IMU。
2 基于IMU-Kinect的定位算法
2.1 坐标系变换
本平台涉及到的坐标系有全局坐标系、机器人坐标系、IMU 坐标系以及Kinect坐标系。从各个传感器获取的数据都是基于其自身坐标系而言的,所以将多个传感器数据进行融合计算时必须先进行坐标转换。本文中将各坐标系数据均转化到全局坐标系进行运算。
首先给定全局坐标系,在系统静止的时候,分别测量机器人、IMU、Kinect坐标系与全局坐标系的欧拉角(φ,θ,ψ),其中IMU 的欧拉角可以通过读取传感器数据进行姿态估计来计算。则各坐标系之间的转换矩阵Cxy通过式(3)得到
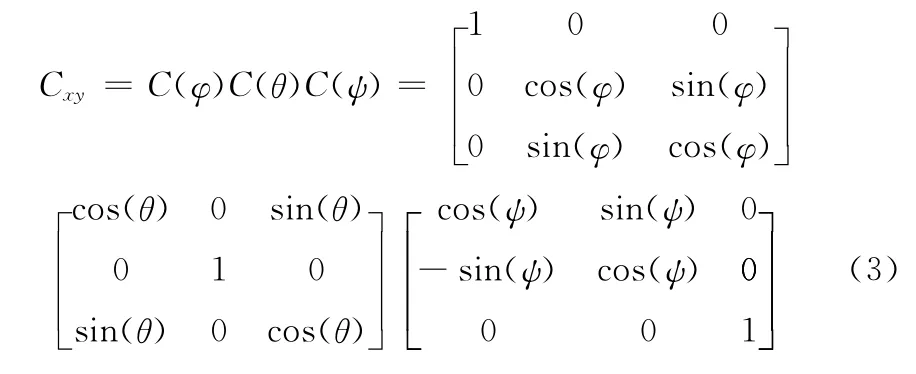
2.2 IMU 位姿估计
(1)姿态解算
IMU 惯性传感器具有三轴加速度计、三轴陀螺仪和三轴地磁仪。陀螺仪测的是角速度的值,进行一次积分得到对应轴的角度,但是由于陀螺仪的漂移和测量噪声的存在,角度的计算会失效,必须进行滤波处理。IMU 常用的姿态解算算法有互补滤波 (CF)和扩展卡尔曼滤波 (EKF)算法。其中EKF算法是将姿态角和偏移角作为状态向量,陀螺仪的测量数据作为输入,而加速度计的测量作为观测模型,进行滤波处理。DCM[10]算法,即direction cosine matrix,是一种互补滤波的算法,目前在IMU 姿态解算中经常使用,可以对6轴或9轴惯性传感单元进行解算,相对于EKF算法,后者更加简单、有效。
DCM 算法先对全局坐标系和IMU 载体坐标系构建方向余弦矩阵,然后将该矩阵求导,得到方向余弦矩阵的微分方程,通过解微分方程,得到矩阵变量,最后转化成欧拉角,即为所求的姿态角。具体描述如下
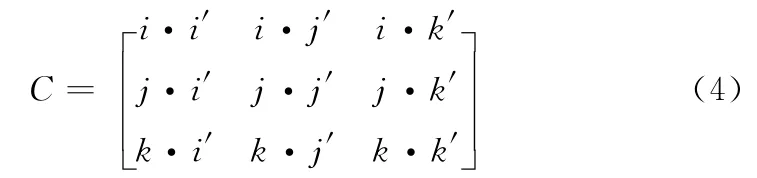
式中:C——方向余弦矩 阵,i′,j′,k′——载体坐标系的单位向量,它是由加速度计和电子罗盘的测量值来确定的,对其求导得到
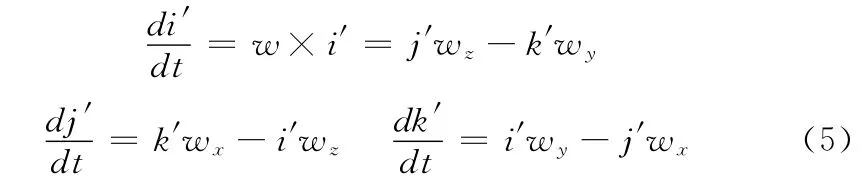
则有微分矩阵
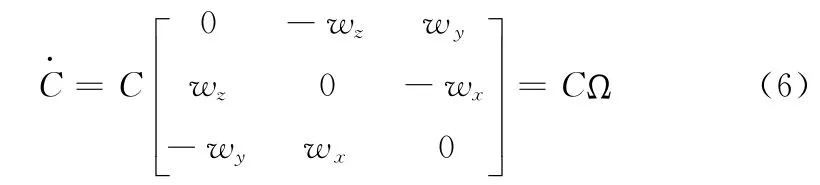
使用DCM 算法求解姿态比EKF 算法更为普遍,其测量结果也更为精确。IMU 姿态解算的结果具备一定的准确性,因此在多传感器融合的过程中,可以予以较多的考虑。
(2)位移估计
通过IMU 进行航位推算,即由线加速度值去除重力分量,然后进行二次积分得到位移值,理论上可以得到航位信息,但是由于噪声的存在、运动过程中的抖动以及姿态解算的误差,加速度的分量无法准确去除,且会造成累积误差,随着运动时间的增长,位移的累积误差会越来越大。普遍的做法是将惯性导航系统与其它导航系统 (如视觉、无线电等)进行组合导航,提高定位的精度。本文采用EKF算法将惯性传感器与视觉传感器进行数据融合,同时将机器人的运动指令作为约束条件。
采用加速度计构建测量模型,状态向量x =(x,y,vx,vy,anx,any),因为机器人的运动是在平面上运动,故z 轴位移和速度、加速度不参与计算。anx,any是加速度的偏移量,包括重力加速度的分量和偏置量。
对加速度的测量值a进行分解可得
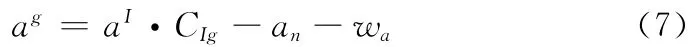
式中:ag——全局坐标系的加速度分解量,aI——加速度计的测得量,CIg——IMU 的坐标系到全局坐标系的转换矩阵,该矩阵随着IMU 的姿态而变化,受IMU 姿态解算的影响。wa——噪声。
则构建观测模型
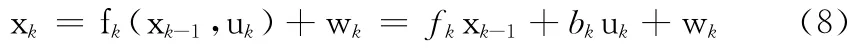
实验结果表明,在IMU 移动的情况下,加速度的偏移量(anx,any)并非为常量,但在短期运动的情况下仍可以常量计算,在机器人静止的时候,可以对该偏移量进行修正,即在运动指令为0时,用式 (9)计算
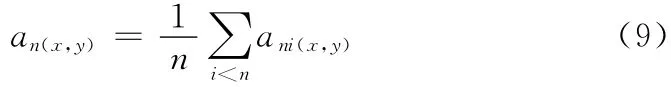
2.3 Kinect位姿估计
使用Kinect进行定位与三维构图的算法,即RGBDSLAM,包含如下几个步骤:
(1)特征提取与匹配:首先从RGB图像中提取出特征点,如SIFT、SURF[11]、ORB、SIFTGPU 等算法,SIFTGPU 算法需要系统配备高性能的显卡,然后使用FLANN算法进行特征匹配。
(2)初始运动估计:根据特征匹配的结果求出相机的运动参数,即采用RANSAC算法,通过迭代,得到一个最优的初始位姿估计值,同时有效的去除误匹配的外点。
(3)位姿优化:通过点云数据的配准,改善初始位姿估计的效果。算法中采用的是广义的ICP (GICP)算法。
(4)图优化:为得到全局一致的地图,需要进行图优化。算法中将得到的位姿作为节点,和邻近帧之间的位姿关系作为边,采用Hog-man算法进行优化。
通过上述步骤得到了最佳位姿估计值和3D 点云地图,该算法后期通过处理可以得到三维栅格地图。
从RGBD-SLAM 算法中可以看出,根据Kinect进行位姿估计的关键是找到一个刚体变换量(R,T),使得代价函数f(R,T)具有最小值
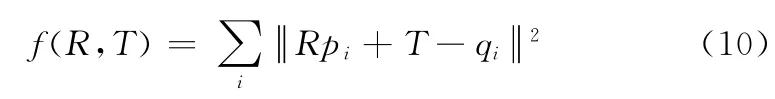
式中:pi——相机移动前测得的匹配点,qi——移动后测得的对应匹配点。R——旋转矩阵,T——平移向量。
根据刚体变换计算得到当前位姿为
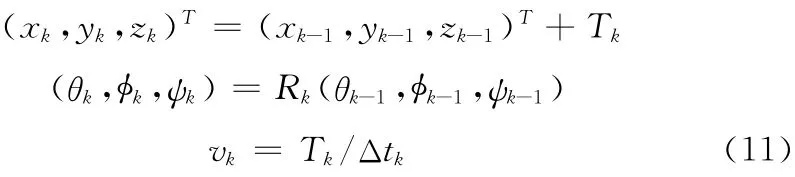
则根据状态向量写出观测模型为

其中,hk=I,vk为噪声,满足高斯白噪声分布,vk~N(0,Rv(v otrust)),噪声协方差Rv(v otrust)[8]的值取决于摄像机扫描到的数据的可信度,由特征点数、RANSAC算法计算的内点数所占比例来确定,可信度越小,噪声协方差值越大。
2.4 基于IMU-Kinect的算法框架
本文提出的改进算法框架如图4所示,在ICP 点云匹配后,将IMU 的预测模型考虑进去,进行位姿融合,得到定位的结果。
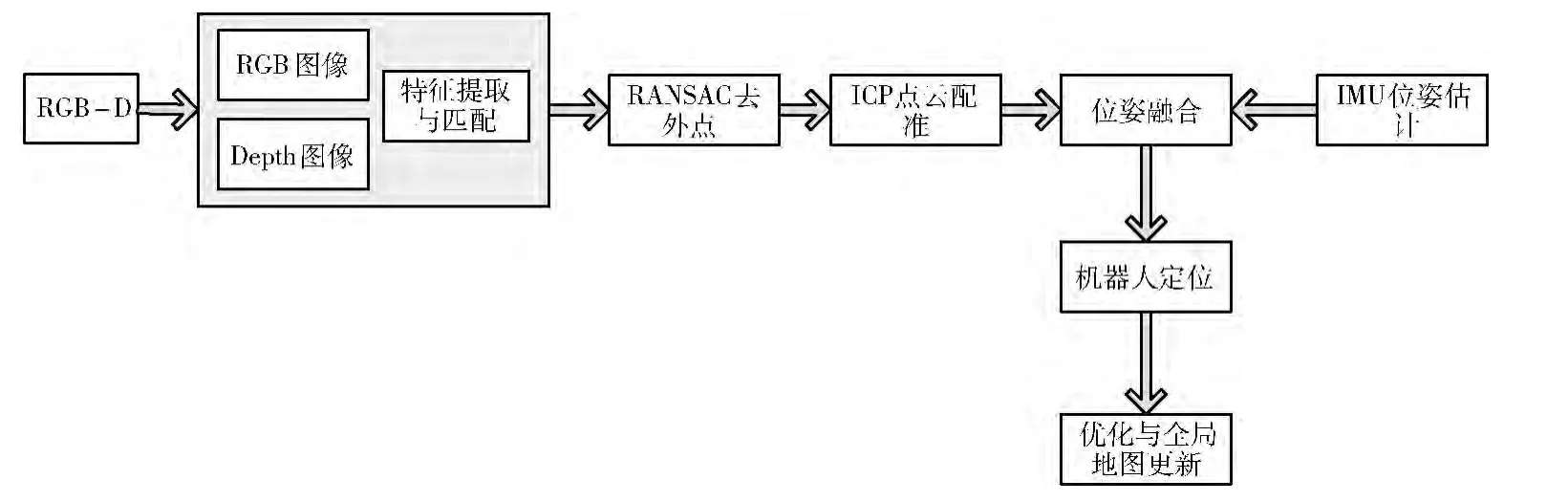
图4 IMU-Kinect的算法框架
机器人的运动指令包含速度和角速度信息,由于三轮全向机器人运行过程中存在漂移,且3个轮子受到的阻力未知,未知的阻力可能会极大的改变运动的方向,因此运动指令内容的参考意义不大。本文主要利用运动指令判断机器人是否静止,将运动指令和运动限制 (机器人线速度<0.6m/s)作为约束条件,构建观测方程。
在进行位姿融合时有如下考虑:
(1)指令为0时,不做滤波处理,位姿信息保持,Kinect测量数据舍弃,对IMU 的加速度偏移量按式 (9)进行修正。
(2)指令不为0,当Kinect特征点丰富时,进行位姿融合处理。
(3)指令不为0,当Kinect特征点小于阈值时,舍弃Kinect数据,采用IMU 进行位姿估计。
位姿融合包含两个部分:姿态和位移。对姿态的融合为:当Kinect与IMU 姿态测量相差小于阈值时,将二者的数据进行1:1的加权平均;当二者的姿态测量大于阈值时,将二者数据进行扩展卡尔曼滤波。对位移的融合为:根据预估模型方程(8)和观测方程(12),进行EKF融合。
融合算法的具体流程如图5所示。
3 实验结果及分析
3.1 软件设计
本文软件的设计是基于ROS系统。ROS是一款开源的机器人软件操作平台,起源于斯坦福大学和Willow Garage公司合作的机器人项目。它提供类似操作系统所提供的功能,同时也提供一些工具程序和库用于获取、建立、编写和运行多机整合的程序。ROS的软件是以功能包的方式组织起来,每个功能包提供节点、消息、服务以及库和其他工具。每个节点相当于一个执行运算任务的进程,节点与节点之间的通信则是采用主题或是服务的形式,如通过发布主题,将消息广播出去,通过订阅主题获取其它节点的消息。
本文的算法是对RGBD-SLAM 算法定位部分的改进,该算法仅仅使用彩色 (RGB)和深度 (Depth)信息进行定位与制图。Endres在ROS上创建了该算法的功能包,它提供了一个rgbdslam 节点。该节点订阅了kinect相关的主题,通过计算机视觉计算,最终给出相机的运动轨迹和3D地图。
本文在该算法的基础上添加了惯性传感的信息和位姿的融合,对应的功能包和节点信息见表1。
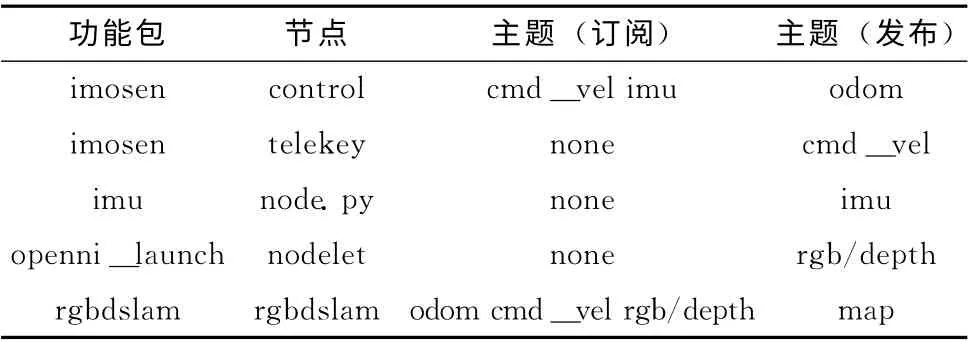
表1 ROS下的功能包
表1中imosen功能包涉及本文机器人在ROS 下的驱动,imu功能包涉及razorIMU 的驱动,openni系列功能包涉及kinect的驱动。telekey节点接收遥控信息并发布cmd_vel主题,即速度、加速度指令;node.py接收惯性传感器的数据,并发布imu主题,即姿态角、9轴数据;control节点订阅cmd_vel、imu主题并发布odom 主题,即里程信息,同时通过蓝牙发送指令控制机器人运行;openni相关节点发布rgb/depth相关的主题;rgbdslam 节点接收odom、rgb/depth主题,在原算法基础上,对位姿进行EKF融合,输出位姿和3D 地图。
3.2 实验结果和分析
本文实验环境为一个约4*5m 的实验室,内有办公桌椅,部分区域为白墙。设定机器人的线速度约0.2m/s,机器人的运行由上位机控制。机器人的初始位置是 (0,0)。
(1)折线运动
图6为两种算法在折线运动中定位结果的比较。机器人的运行路线为沿Y 轴运动一段距离,之后做一段折线运动,然后再沿X 轴运动。折线区域的特点是,由于Kinect离障碍物很近,特征点急剧减少,甚至降为0。图6 (a)为两种算法下位移的对比,其中waypoint为事先测定好的路径关键点。从图中可以看出,在折线区域,由于特征点不足,RGBD 算法定位失效,没有捕捉到这部分的轨迹,而IMU-Kinect算法利用IMU 数据参与运算,能够捕捉到折线运动。此外从图中可以看到改进的算法比RGB-D 算法定位追踪的效果更好。图6 (b)为姿态角的对比,机器人的初始姿态角为0 度,停止点的姿态角为-90 度,即-1.57rad,在折线区域没有改变姿态角的大小,仍为0 度。从图中可以看出两种算法都能捕捉到角度的改变,但是改进的算法捕捉的细节更加完善,得到的结果也更加准确。
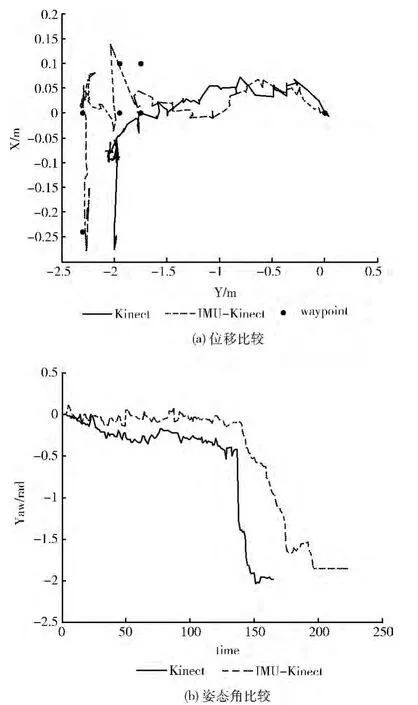
图6 折线运动下Kinect与改进算法定位结果的比较
(2)椭圆运动
图7为两种算法在椭圆运动中定位结果的比较。机器人的运行路线为一段椭圆的运动。从图7 (a)的右上角可以看出两种算法都能回归到起点,RGBD 算法比改进的算法得到的轨迹更加平滑,但改进的算法比RGB-D 算法更贴近于路径关键点。图7 (b)为姿态角的对比,椭圆运动中机器人初始姿态角为0度,随着旋转慢慢运动到-180度,再到-360度。从图中可以看到两种算法都能捕捉到角度的改变,具有收敛性。
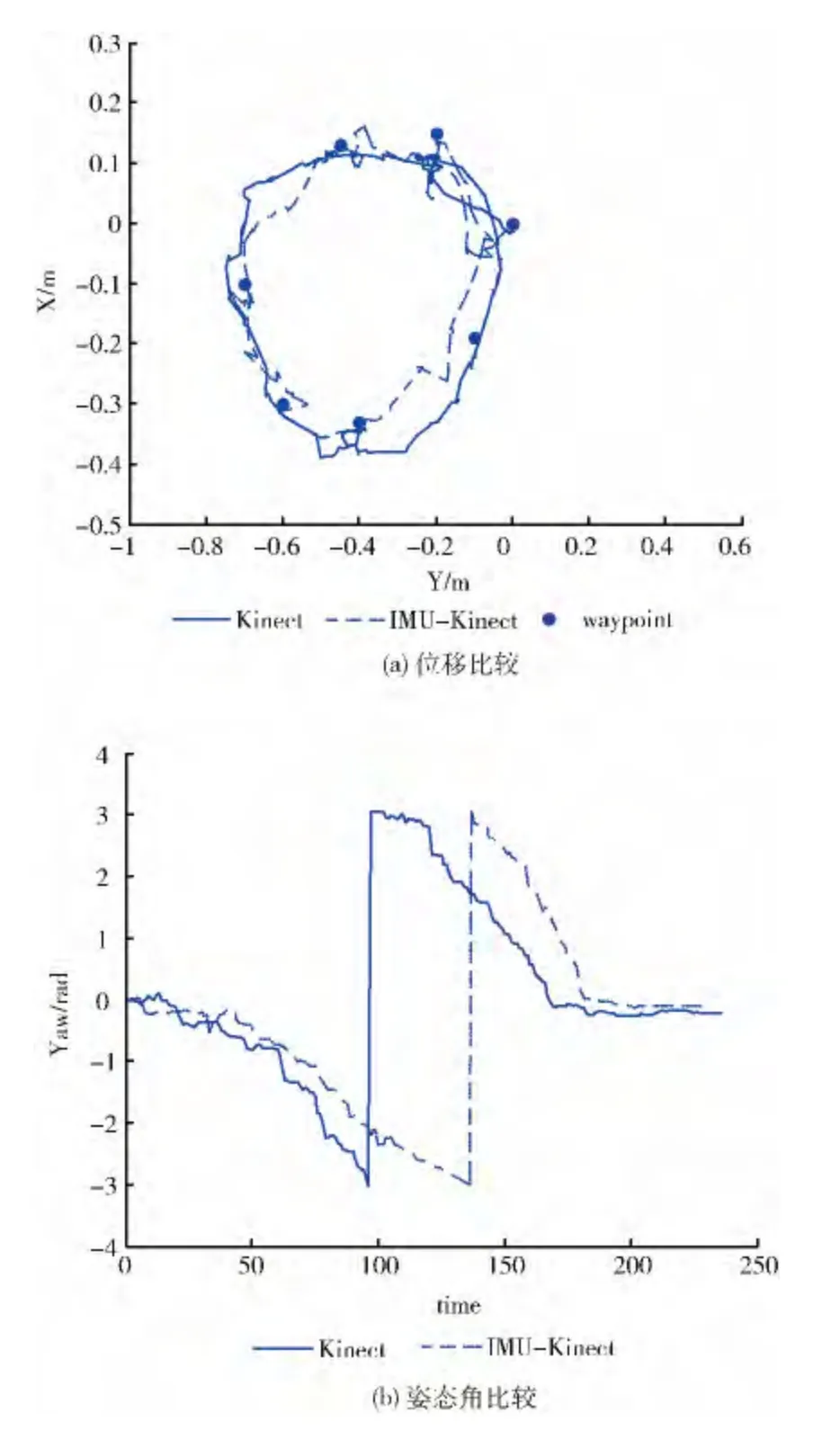
图7 椭圆运动下Kinect与改进算法定位结果的比较
4 结束语
本文提出了一种以RGBD-SLAM 算法为基础的改进的定位与构图算法,结合九轴惯性传感器IMU 对姿态的解算和对加速度的测量,对Kinect位姿估计的结果进行EKF数据融合,实现最优运动估计。通过实验对以上两种算法进行了比较和分析,实验结果表明相对于传统的RGBDSLAM 算法,本文提出的算法提高了计算效率和定位精度,能更准确的追踪机器人的位姿。
[1]Henry P,Krainin M,Herbst E,et al.RGB-D mapping:U-sing Kinect-style depth cameras for dense 3Dmodeling of indoor environments [C]//International Journal of Robotics Research,2012,31 (5):647-663.
[2]Felix Endres,Jürgen Hess,Daniel Cremers,et al.An evaluation of the RGB-D SLAM system [C]//In Proc of the IEEE Int Conf on Robotics and Automation,2012.
[3]Kerl C,Sturm J,Cremers D.Robust odometry estimation for RGB-D cameras[C]//In Proc of the IEEE Int Conf on Robotics and Automation,2013.
[4]Audras C,Comport AI,Meilland M,et al.Real-time dense appearance-based SLAM for RGB-D sensors [C]//In Proc Australian Conf Robotics and Automation,2011.
[5]Stuckler J,Behnke S.Model learning and real-time tracking using multi-resolution surfel maps[C]//In AAAI Conf on Artificial Intelligence,2012.
[6]Bouvrie BD.Improving RGBD indoor mapping with IMU data[D].Holland:Delft University of Technology,2011.
[7]Fredrik Hjelmare,Jonas Rangjs.Simultaneous localization and mapping using a Kinect in a sparse feature indoor environment[D].Sweden:Linkping University,2012.
[8]Thibault Hervier,Silvere Bonnabel,Francois Goulette.Accurate 3D maps from depth images and motion sensors via nonlinear Kalman filtering [C]//In Proc of the IEEE/RSJ Int Conf on Intelligent Robots and Systems,2012.
[9]Sparkfun Electronics.9 degrees of freedom-razor imu [EB/OL].https://www.sparkfun.com/products/10736,2014.
[10]Starlino Electronics.DCM tutorial-An introduction to orientation kinematics [EB/OL]. http://www.starlino.com/dcm_tutorial.html,2011.
[11]Tseng SP,Li WL,Sheng CY,et al.Motion and attitude estimation using inertial measurements with complementary filter[C]//In Proceedings of 8th Asian Control Conference,2011:863-868.

