民航旅客订票行为细分及群体特征分析

冯 霞，徐冰宇，卢 敏

（1.中国民航大学 计算机科学与技术学院，天津300300；2.中国民航信息技术科研基地，天津300300）

0 引 言

越来越多的航空公司开始实行客户关系管理系统（customer relationship management，CRM）［1］，并对旅客进行细分［2］，希望发现具有不同价值的旅客群，并针对不同价值的旅客群实行不同的营销策略，提升航空公司服务质量，从而提高航空公司收益。然而客户细分工作在民用航空业起步比较晚，发展比较落后。目前航空公司大多数是按旅客购买机票的票价或者其累计的里程距离进行细分，例如营销专家Bob Stone提出了RFM 法［3］；南京航空航天大学的罗亮生等对传统的RFM 指标做了适当的调整，确定了L，R，F，M，C这5个指标为航空公司客户价值发现的参数［4］。实际上，上述民航旅客细分方法只是发现了旅客的价值，并未指出旅客群体的行为特征，如旅客具备何种乘机习惯等，进而无法支撑航空公司面向不同行为偏好群体的旅客开展个性化营销。

为了解决上述问题，本文基于民航旅客订票数据并结合传统RFM 模型，提出一种TCSDG （time，class，seat，discount，group）模型，模型的核心思想是：采用旅客出行时间、舱位、座位和票价折扣描述旅客的乘机习惯，并使用K－means算法对旅客聚类，进而将旅客划分为若干个簇。由于民航旅客订票数据规模巨大，传统K－means算法难以处理。为此，本文提出了基于Hadoop的K－means并K－means行化算法以应用于大规模民航旅客订票数据的旅客细分。

1 基于TCSDG 的民航旅客行为偏好模型

1.1 传统RFM 模型

RFM 模型是由营销专家鲍比斯通 （Bob Stone）提出的。在民航领域，R 指旅客最近一次乘坐飞机距离当前日期的天数；F 指旅客在某一段时间内乘坐飞机的次数；M指旅客购买机票的机票票价。RFM 模型认为那些最近出行时间较短、出行频率较高以及所购买的机票票价较高的旅客是相对价值较高的旅客，即航空公司需要关注的旅客［5，6］。

1.2 TCSDG 模型的构建

RFM 模型由于容易理解、计算简单等特点广泛被各行业用于客户关系管理。然而也正是因为其只使用R、F、M这3个属性来对旅客进行评价，忽略了旅客的其它属性，并不能全面的反映旅客的行为偏好，因此本文根据实际旅客订票数据的特点结合传统的RFM 模型提出一种更为全面反映旅客行为偏好的TCSDG 模型。模型中的各参数含义如下：T：Time，表示旅客出行时间；C：Class，表示旅客所在舱位；S：Seat，表示旅客所在座位；D：Discount，表示旅客购票的折扣；G：Group，表示旅客是否跟团出行。

选择这5个参数是因为这5个参数在旅客订票时是由旅客根据自己的意愿选择的，且对航空公司不同航班的客座率有直接影响，进而影响航空公司总体收入。由于实际订票数据的格式不能直接通过TCSDG 模型进行计算，因此按如下方法进行处理。

对于参数T，由于出行时间是连续的时间值，而旅客对出行时间的偏好主要体现为对不同时间段的偏好。本文将时间离散成3个时间段，0时0分～11时59分为上午，12时00分～17时59分为下午，18时00分～23时59分为晚上。

对于参数C，实际中舱位代码有F 舱 （头等舱公布价），A 舱 （头等舱免折），C 舱 （公务舱公布价），D 舱（公务舱免折），Y 舱 （普通舱公布价）等。对于航空公司，舱位类型主要有头等舱、商务舱和经济舱三大类。本文将F舱、A 舱处理为F＝1；将C舱、D 舱处理为C＝1；将其它舱位代码处理成Y＝1。

对于参数S，反映了旅客对于靠窗或者不靠窗座位的偏好。目前国内的座位分布主要以中国国际航空公司 （简称国航）和中国南方航空公司 （简称南航）两个航空公司为代表，其中国航座位分布中座位代码A、F 代表靠窗座位，而南航座位分布中座位代码A、K 代表靠窗。本文将座位代码A、K、F处理为S＝1，其它则S＝0。

对于参数D，因为同旅客可能有多条订票记录，本文使用旅客所有订票记录中折扣的平均值。

对于参数G，若订票记录中有团队名则G＝1，没有则G＝0。

2 基于TCSDG 模型的旅客聚类

通过构建1.2节中提出的TCSDG 模型，我们可以得到旅客的行为偏好，为了进一步对旅客进行细分，通过聚类算法可以将具有相同行为偏好的旅客聚成一簇。算法流程如图1所示。

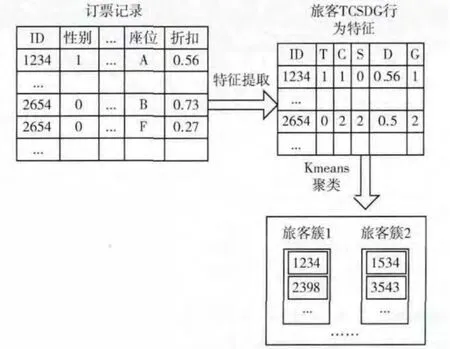
图1 基于TCSDG 模型的旅客细分

聚类是一种重要的数据挖掘算法，其目标是将数据集划分为若干簇，使得同一簇内的点相似度较高，而不同簇中的点相似度较低［7，8］。K－means是经典的聚类算法，其应用已比较成熟，相比于其它聚类算法，其有易于理解，收敛速度快等特点。K－means具体算法步骤如下：

输入：待聚类数据集N 以及簇的数目k。

输出：使平方误差最小的k个簇。

（1）从数据集N 中选择k 个对象作为初始簇中心mi（i＝1，2，3，…，k）；

（2）根据式 （1）计算数据集N 中每个元素p到k个簇中心的距离d（p，mi）；

（3）找到每个元素p最小的d（p，mi）并将元素p归入与mi所属的簇中；

（4）遍历数据集N 中所有元素，使用式 （2）更新mi簇中心的值；

（5）重复步骤 （2），直到平方误差小于设定值。

这里的距离公式使用欧式距离，即

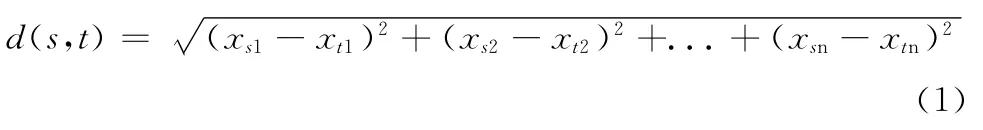
其中s＝（xs1，xs2，…，xsn），t＝（xt1，xt2，…，xtn）是两个n维数据对象。

更新簇中心公式如下

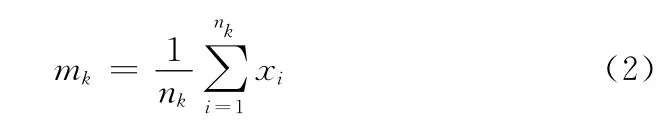
式中：mk——第k个簇的簇中心，nk——第k个簇中元素个数。

平方误差定义如下

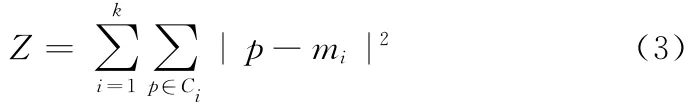
式中：p——簇Ci的元素，k——簇数。

3 基于TCSDG 模型的民航旅客细分并行算法

在面对航空公司海量历史订票数据时，单机由于受内存、处理能力等方面限制，表现为计算时间过长甚至无法进行计算。因此，本文结合Hadoop并行计算平台将基于TCSDG 模型的旅客聚类算法并行化。

3.1 Hadoop

Hadoop是Apache公司开发的分布式系统基础架构，可以使用它将大量廉价设备组成一个分布式集群，构成一个高性能的并行计算平台。Hadoop框架的核心是分布式文件系统 （Hadoop distributed file system，HDFS）和MapReduce，前者实现了海量数据的存储，后者提供了海量数据的计算模型。MapReduce借鉴了函数编程的思想，将大规模的数据处理任务抽象成Map和Reduce两种操作。在Map函数中处理一系列键值对＜key，value＞，并处理输出一系列中间键值对＜key，list＜values＞＞，所有具有相同key值的value值传给同一个Reduce函数，Reduce函数接收Map函数输出的键值对，并对每一个key 按需要计算value值，并输出键值对＜key，value＞［9－11］。

3.2 并行化K－means聚类算法

K－means算法的主要思想是将数据集中的每个元素分配到离它距离最近的类簇中，并使得所有类簇中平方差最小；使用K－means算法在读取元素以及分配不同元素到其最近的类簇时的操作是相互独立的，这也给算法并行化提供基础。

并行化K－means算法流程如下：

步骤1

初始化k个中心点，将k个中心点的信息存入HDFS，信息包括簇标示符，该中心点向量。

步骤2

Map过程：

输入key－value值 （数据偏移量，内容）；

计算此点与哪个中心点距离最近；

输出key1－value1值 （簇号，元素值）；

Reduce过程：

输入key1－value1值 （簇号，元素值）；

计算此类新的中心点，质心距离等，更新HDFS中中心点向量信息；

输出key2－value2值 （簇号，此簇所有元素内容）；

步骤3

计算每个类中新的中心点与原来中心点的距离，若距离大于给定阈值则重复步骤2，若距离小于给定值则输出结果。

在步骤1中由于并行计算时每台计算节点均需要访问簇中心的信息，因此将簇中心信息存储于HDFS中，使得集群中的每台计算机均可以读写。

在步骤2中，计算元素和不同簇中心点的距离只需要读取HDFS中的簇中心信息，因此可以将不同的数据块分给不同的节点进行并行计算，集群的节点通过Map函数按＜key，value＞的形式读入部分数据，其中key为数据记录偏移量，value为一行记录内容，计算此元素与各簇中心的距离，并标记此元素所属最近的簇类；然后输出＜key1，value1＞，其中key1是距离最近的簇的标示符，value1 标示该元素值。Reduce函数接收Map 函数的输出值，所有key值相同的value会被传到一个Reduce函数中，因此一个Reduce函数中包含一个簇的所有元素信息。在Reduce函数中可以计算新的聚类簇中心以及每一簇的平方误差，更新HDFS中的簇中心信息并根据平方误差决定算法是否继续迭代，Reduce函数输出＜key2，value2＞，其中key2表示簇标示符，value2表示属于该簇的所有元素的信息。

4 实验及分析

4.1 实验平台及数据

实验中搭建了1台控制节点，4台计算节点的Hadoop并行计算集群，集群中电脑配置为Inter（R）Core（TM）2 Quad 2.89Ghz Cpu，4GB 内 存，电 脑 操 作 系 统 为Ubuntu12.0，Hadoop版本为1.0.4。

本文中采用的实验数据为中国民航订座系统中2010年1月至2011 年12 月两年的真实订票数据，数据大小为50GB，有17个属性，本文只列举使用到的属性，样例数据见表1，为了保护旅客隐私，我们使用加密算法将身份证加密，但是可以保证每个旅客对应唯一的身份证ID。

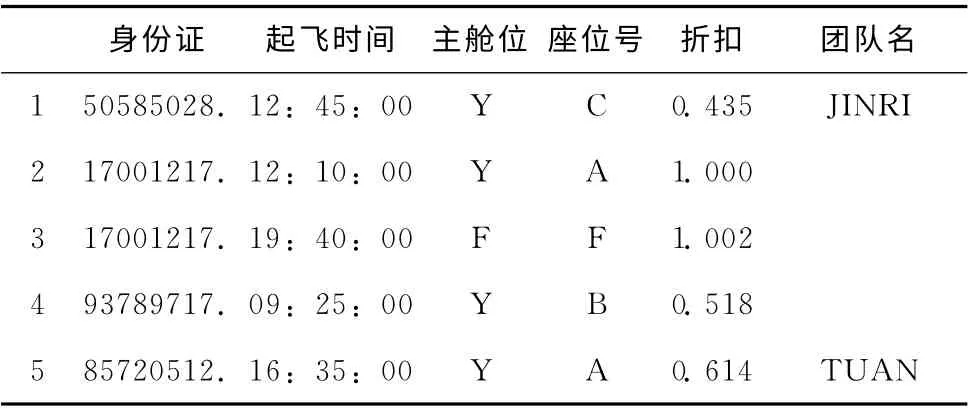
表1 样例数据

4.2 并行K－means聚类算法有效性和高效性验证

为了验证并行K－means算法的有效性，我们分别使用并行K－means算法和传统K－means算法对标准数据集iris（鸢尾花）数据集进行聚类，结果见表2、表3。

表2 传统K－means聚类结果

表3 并行化K－means聚类结果

从表2、表3中可以看出，并行K－means聚类算法的效果和传统K－means算法效果一致，其中中心点有微小差异是因为在选取初始聚类中心时采用随机选取的方式。

为了验证并行K－means算法的高效性，我们从实验数据中分别截取1000 条、2000 条、…、500000 条记录，使用并行K－means算法和普通K－means算法分别进行聚类，两种算法耗时见表4。

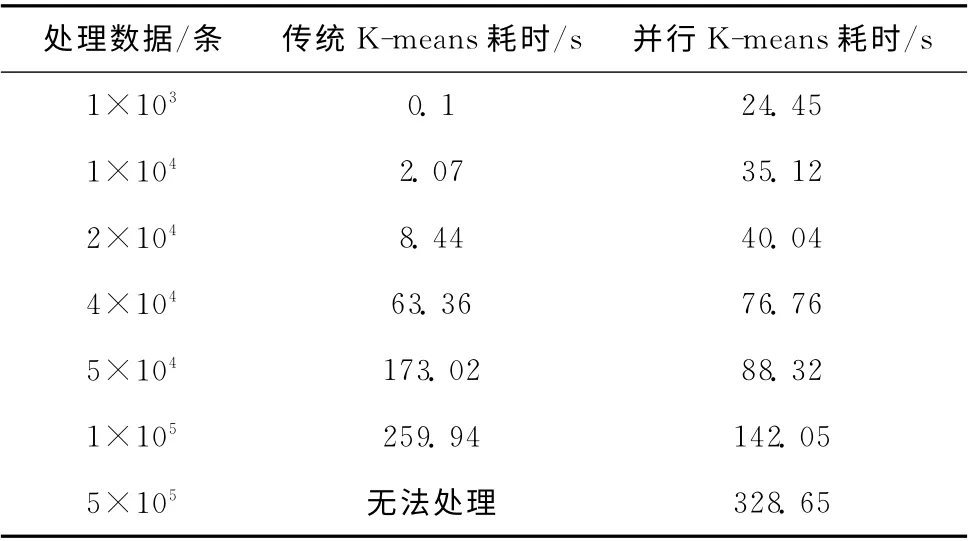
表4 传统K－means算法和并行K－means算法消耗时间对比

从表4可以看出，当数据量较小时 （少于5×104条）时，传统K－means执行时间较短，这是因为并行K－means算法消耗了大量时间读取数据以及进行节点间通信；随着数据量增大，读取数据以及节点间通信消耗的时间对并行Kmeans算法的整体运行时间影响逐渐减小，并行K－means算法逐渐优于传统K－means算法；当数据量增加到足够大时，传统K－means算法会受制于内存、计算能力等因素而难以处理，而并行K－means算法使用HDFS存储文件则不受影响。

4.3 旅客TCSDG 特征计算

实验数据中有部分赃数据 （例如被取消订单的记录、团队名缺失的记录），需要对数据清洗，删除被取消的订单数据，补全缺失的数据项等。

由于订票数据中存在同一旅客具有多条订票记录的情况，我们需要将一个旅客的多条订票数据处理成一条数据，首先按照1.2节方法计算每条记录的TCSDG 特征值，然后按照数据中的ID 值，将同一ID 的数据进行合并。由于数据量的庞大性，且计算不同ID 的TCSDG 特征值间相互独立，采用Hadoop并行计算平台进行计算。以表1的样例数据为例，按TCSDG 模型预处理后的结果见表5。

表5是表1样例数据按照TCSDG 模型计算并将相同ID 的旅客数据合并的特征值。例如，表1中第2、3行数据代表同一旅客17001217.的记录，在表5 中已处理成一条数据，表示旅客17001217.乘坐下午航班1次，乘坐晚上航班1次，购买经济舱1次，购买头等舱1 次，两次均坐在靠窗的位置，两次平均折扣1.001，两次均是单独出行。

4.4 基于TCSDG 模型的旅客聚类

K－means算法的初始聚类簇数k对算法具有很大的影响，然而在对具体数据进行聚类时k 值通常是不确定的［12］。我们分别将k值设定为2、4、6、…、22等多个值进行聚类，并计算最终聚类结果的平方误差，计算结果如图2所示。

从图2中可以看出随着k值的增加，聚类结果的平方误差在减小，这不难理解，k值越大则聚出的簇越多，极限情况当每一个元素单独成一簇时，则平方误差为0。在图2中当k＜14时，平方误差的降幅较大，当k＞14时，平方误差的降幅较平稳，因此本文中将初始类簇个数k 设置为14。

表5 旅客TCSDG 特征值

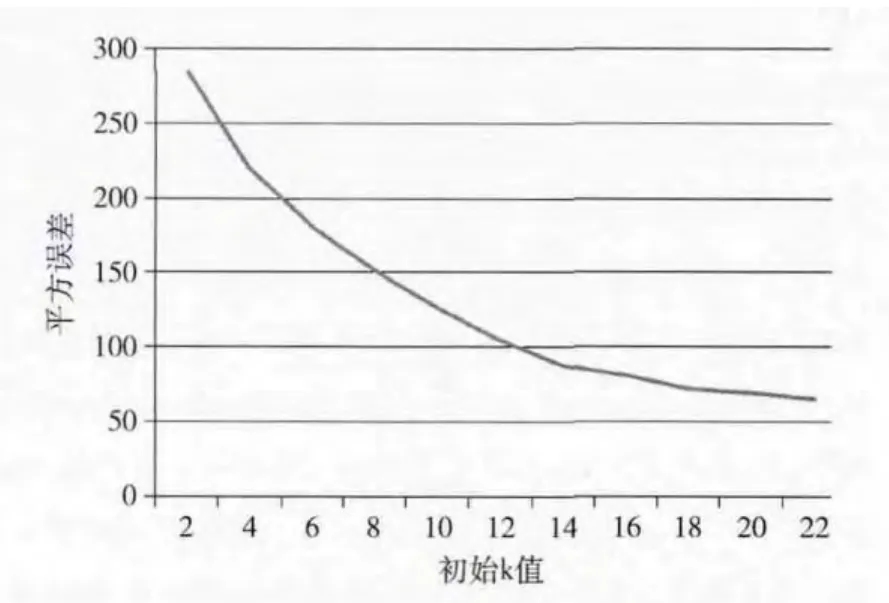
图2 不同初始k值聚类平方误差

在确定初始类簇个数后，对4.3节中得到的旅客TCSDG 特征数据按照3.2节提出的并行K－means聚类算法进行聚类，聚类后各簇不同行为偏好的人数比例见表6，第一列表示簇编号，其中每一行表示一簇中不同偏好的人数占此簇人数的比例，每一行的上午、下午、晚上人数百分比和为100%；每一行的经济舱、商务舱、头等舱人数百分比和为100%、每一行靠窗、不靠窗人数百分比和为100%，每一行团队、单独人数百分比和为100%，每一行折扣为此簇旅客购票折扣平均值。

为了更好的看出每簇旅客的行为偏好，我们将其中几簇的旅客统计成图，如图3～图5所示。

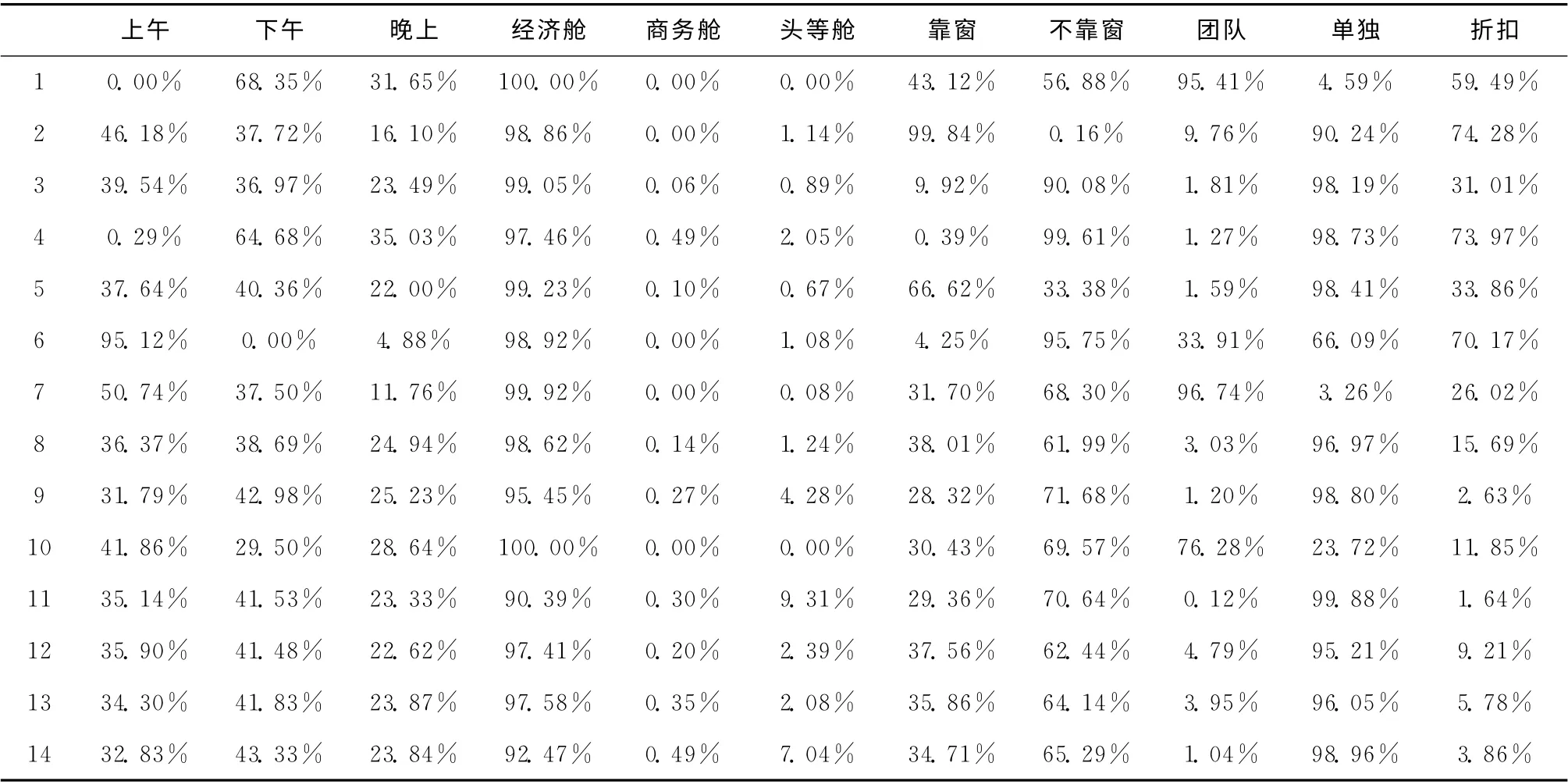
表6 聚类结果

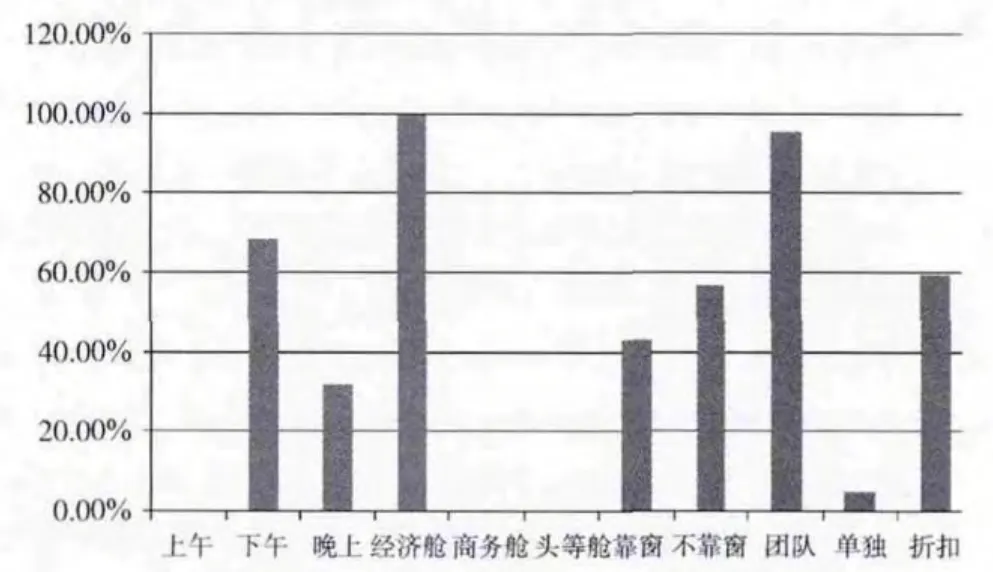
图3 第一簇旅客行为偏好

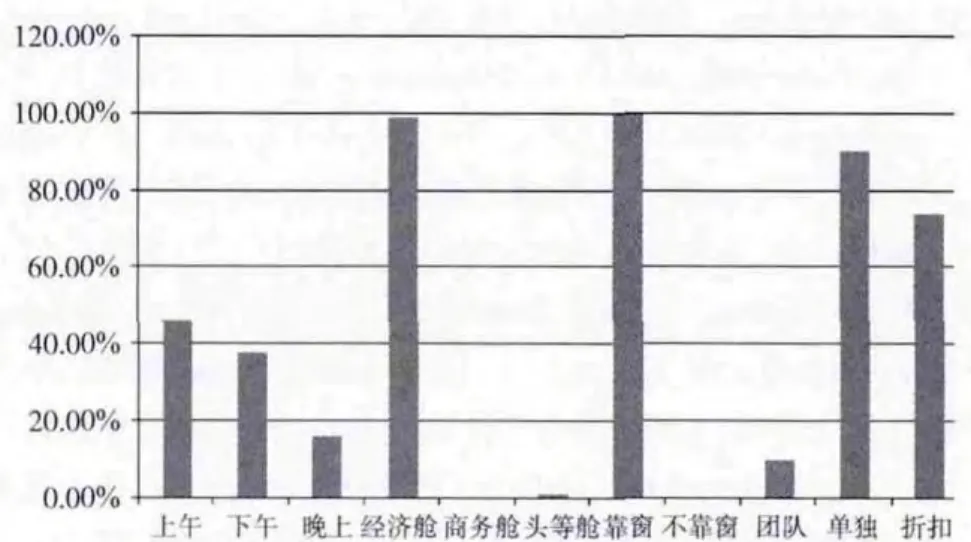
图4 第二簇旅客行为偏好

图3～图5分别是第一、二、三簇旅客的乘机时间、乘机舱位、座位等信息的比例。可以看出第一簇的旅客偏向乘坐下午和晚上的航班，偏向选择经济舱，对座位位置不太敏感，偏向团队出行，偏向6折的机票；第二簇的旅客对出行时间不太敏感，偏向选择经济舱，部分选择头等舱，偏向靠窗的座位，偏向单独出行，偏向选择7至8折机票；第三簇的旅客对出行时间不太敏感，偏向选择经济舱，部分选择头等舱和商务舱，偏向选择不靠窗的座位，偏向单独出行，偏向3 折机票；……剩下其它类簇的信息从表6中也都可以看出，这样有利于航空公司有针对的营销，对不同行为偏好的类簇提供不同的个性化推荐服务，比如对第一簇中的旅客推荐下午和晚上时间的航班，推荐经济舱，推荐6折的机票；对第二簇中的旅客推荐经济舱和头等舱，推荐靠窗的座位，推荐7折的机票；对第三簇的旅客推荐不靠窗的位置，推荐折扣较低的机票等。

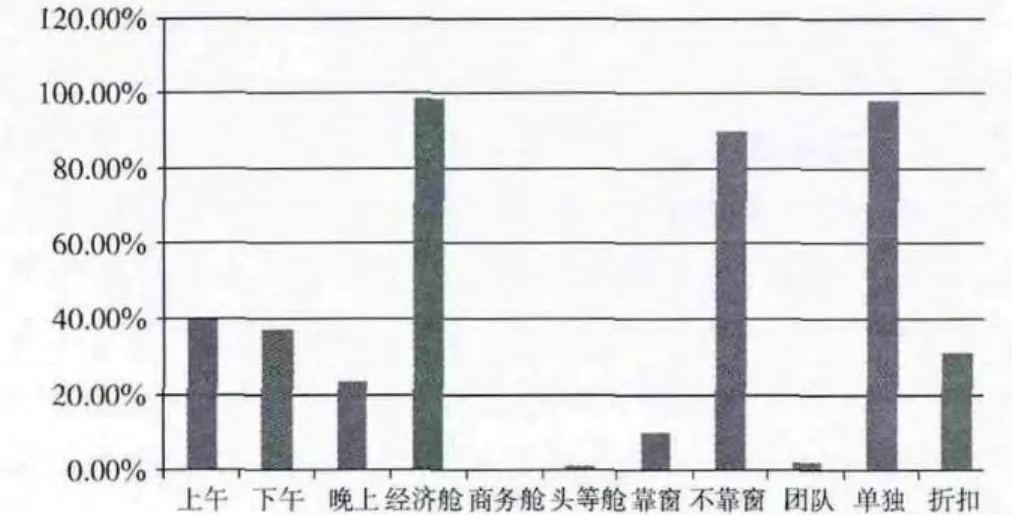
图5 第三簇旅客行为偏好

5 结束语

旅客是航空公司最重要的收入来源，如何提升航空公司服务，将航空公司的旅客按不同需求划分成不同的群体，并针对不同需求的群体提供个性化的推荐服务一直是航空公司客户管理工作的重点。本文提出一种TCSDG 模型来描述旅客行为偏好，并根据旅客的不同行为偏好等对旅客进行更全面的细分，有利于改善航空公司个性化的营销服务；并将本文提出的算法结合Hadoop并行计算平台使得本文算法可以并行计算，从而可以对航空公司海量的订票数据进行处理。

［1］Liu Y，Ram S，Lusch RF.Multicriterion market segmentation：A new model，implementation，and evaluation ［J］.Marketing Science，2010，29 （5）：880－894.

［2］FANG Anru，YE Qiang，LU Qi，et al.Customer segmentation framework model based on data mining ［J］.Computer Engineering，2009，35 （19）：251－253 （in Chinese）. ［方安儒，叶强，鲁奇，等.基于数据挖掘的客户细分框架模型 ［J］.计算机工程，2009，35 （19）：251－253.］

［3］XU Xiangbin，WANG Jiaqiang，TU Huan，et al.Customer classification of E－commerce based on improved RFM model［J］.Journal of Computer Applications，2012，32 （5）：1439－1442 （in Chinese）. ［徐翔斌，王佳强，涂欢，等.基于改进RFM 模型的电子商务客户细分 ［J］.计算机应用，2012，32（5）：1439－1442.］

［4］LUO Liangsheng，ZHANG Wenxin.Research of method customer segment of airlines based on database of frequent flyer［J］.Modern Business，2008 （23）：54－55 （in Chinese）.［罗亮生，张文欣.基于常旅客数据库的航空公司客户细分方法研究 ［J］.现代商业，2008 （23）：54－55.］

［5］SHUAI Bin，DENG Shaowei，HUANG Lixia.Railway express freight consumer market segmentation based on improved RFM model［J］.Journal of Railway Science and Engineering，2014，11 （1）：112－117 （in Chinese）.［帅斌，邓绍蔚，黄丽霞.基于改进RFM 模型的铁路快捷货运客户市场细分方法［J］.铁道科学与工程学报，2014，11 （1）：112－117.］

［6］LV Bin，ZHANG Jindong.Commercial bank marketing decision analysis based on RFM model［J］.Statistics and Decision Making，2013，29 （14）：65－67 （in Chinese）. ［吕斌，张晋东.基于RFM 模型的商业银行营销决策分析 ［J］.统计与决策，2013，29 （14）：65－67.］

［7］TONG Xuejiao，MENG Fanrong，WANG Zhixiao.Optimization to k－means initial cluster centers［J］.Computer Engineering and Design，2011，32 （8）：2721－2723 （in Chinese）.［仝雪姣，孟凡荣，王志晓.对k－means初始聚类中心的优化［J］.计算机工程与设计，2011，32 （8）：2721－2723.］

［8］ZHOU Aiwu，YU Yafei.The research about clustering algorithm of K－Means ［J］.Computer Technology and Development，2011，21 （2）：61－65 （in Chinese）. ［周爱武，于亚飞.K－Means 聚 类 算 法 的 研 究 ［J］.计 算 机 技 术 与 发 展，2011，21 （2）：61－65.］

［9］LU Jiaheng.Hadoop in action ［M］.Beijing.China Machine Press，2011 （in Chinese）.［陆家恒.Hadoop实战 ［M］.北京：机械工业出版社，2011.］

［10］White T.Hadoop：The definitive guide ［M］.O’Reilly Media，Inc，2009.

［11］CUI Jie，LI Taoshen，LAN Hongxing.Design and development of the mass data storage platform based on Hadoop ［J］.Journal of Computer Research and Development，2012，49（S1）：12－18（in Chinese）. ［崔杰，李陶深，兰红星.基于Hadoop的海量数据存储平台设计与开发 ［J］.计算机研究与发展，2012，49 （S1）：12－18.］

［12］ZHOU Shibing，XU Zhenyuan，TANG Xuqing.Method for determining optimal number of clusters in ［J］.Journal of Computer Applications，2010，30 （8）：1995－1998 （in Chinese）.［周世兵，徐振源，唐旭清.K－means算法最佳聚类数确定方法 ［J］.计算机应用，2010，30 （8）：1995－1998.］