基于区域划分和三角网格优化的基段选择算法

吴禄慎，王伟杰，陈华伟，冯 伟

（南昌大学 机电工程学院，江西 南昌330031）

0 引 言

构建四边形网格的所有算法可以归类为直接法［1］和间接法［2］。直接法不经过中间环节，把点云直接生成四边形网格。由于需要处理的点云数据量巨大、模型形状和边界复杂，研究人员很难直接获得分布均匀、拓扑成四边形的网格模型，因此难以达到B 样条曲面重构四边形参数域的要求。间接法先使用成熟Delaunay三角剖化［3］算法构建散乱点云的三角网格，建立空间网格拓扑关系，然后把三角网格转化为四边形网格。与直接法相比，间接法程序更易实现，并且能生成质量较好的四边形网格。

在许多工程分析条件下，沿区域边界单元尤其重要，理想情况是网格单元齐整地排列在区域边界处。依据此理论，文献 ［4］将生成三角形曲面网格的前沿推进算法扩展到四边形曲面网格生成，新算法从边界处逐个单元前移前沿，解决了逐排推进铺路法中出现的鲁棒性问题，能够生成理想的四边形网格；刘晶等［2］对Q－Morph算法中确定侧边方法进行了改进，虽然使网格转化过程中残留三角形单元数目大大减少，但是不能保证生成四边形网格的质量；陈阳等［5］改进了前沿段生长算法，相比原算法，很好地解决了在几何质量较差、疏密变化较大的三角网格区域不能生成规则四边形网格的问题，并通过改变网格顶点度和设置生长约束条件，一定程度上改善了四边形网格质量，但该算法对疏密度差别较大的三角网格区域使用相同方法生成四边形，影响网格转化的效率和质量。

实验发现在哪一个前沿段上形成四边形决定四边形生长方向且严重影响最终生成四边形网格的质量，因此如何选择基段成为网格转化的关键。本文在生成点云前，使用一种基于多极线约束的重叠点云删除算法［6］，以避免产生冗余点。对生成的点云数据使用曲率特征简化［7］后，划分出平坦区和非平坦区，然后三角化点云，优化形成的三角网格，最后根据提出的基段选择算法确定待生成四边形的起始边。

1 名词解释

节点、单元、棱和段：在网格生成中，节点和单元是基本实体。节点是点云的数据点，单元是一系列节点以逆时针方向首尾相连而成。棱是单元的一侧，连接两个端节点。为了区分一般棱，把位于三角网格与四边形网格边界上的棱称为段。如图1所示。

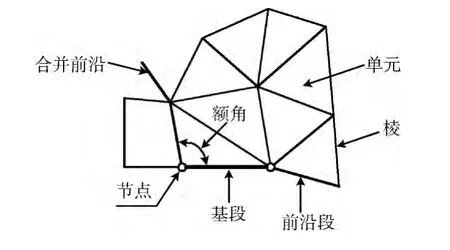
图1 名词解释

合并前沿、前沿段、额角和基段：合并前沿是待转换区域中所有边界段的集合。合并前沿把已转换区域从待转换区域中分离开，且必须形成至少一个闭合环。合并前沿上的棱为前沿段；在前沿段两端节点处与其相邻前沿段的夹角称为额角。作为形成四边形起始边的前沿段称为基段。如图1所示。

2 标记平坦区和非平坦区

定义1 设X＝ ｛x1，x2，…，xn｝是将要建立曲面S上的n 个点集，集合X 中离任意点xi最近的k 个点称为xi的K－邻域，记为K（xi）。

本文利用树的层级结构对空间中每一个点进行K－邻域搜寻［8］。然后在每一个点如xi的K－邻域基础上拟合有约束的最小二乘平面P（xi）作为将要建立曲面在该点的切平面，K（xi）的形心位置是切平面的中心点oi。计算切平面P（xi）的单位法矢ni，使K（xi）内的k 个点到这个切平面距离的平方和达到最小，然后以ni为xi点的单位法矢。为了计算ni的值，需建立K（xi）的协变矩阵

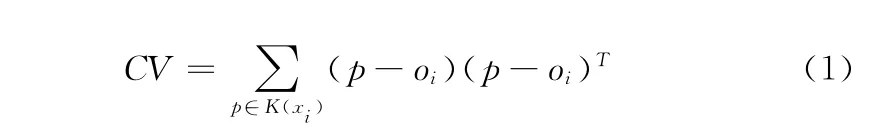
式中：（p－oi）是列向量， （p－oi）T是 （p－oi）的转置，CV 是一个对称的半正定3×3 矩阵，记矩阵CV 的最小特征值所对应的单位特征向量为ei，法矢ni取对ei同向化处理后所对应的值。将求得所有数据点的法矢量存在一个一维数组Vector中，顺序与原始数据点数组相对应。

如果K（xi）准确表达了将要建立曲面S 在xi点附近的几何形状，那么曲面S在xi点上的曲率越大，点xi到切平面P（xi）的垂直距离越大，曲面S在xi点上的曲率越小，点xi到切平面P（xi）的垂直距离越小。可得出下面的定义：

定义2 设X＝ ｛x1，x2，…，xn｝是将要建立曲面S上的n 个点集，对每一个数据点xi用它的K－邻域拟合将要建立曲面S 在该点处的切平面P（xi），D＝ ｛d1，d2，…，dn｝为每一个点到它的切平面距离的绝对值

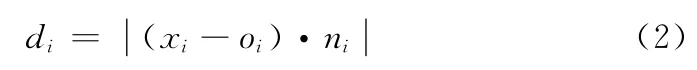
切平面距离计算如图2所示。

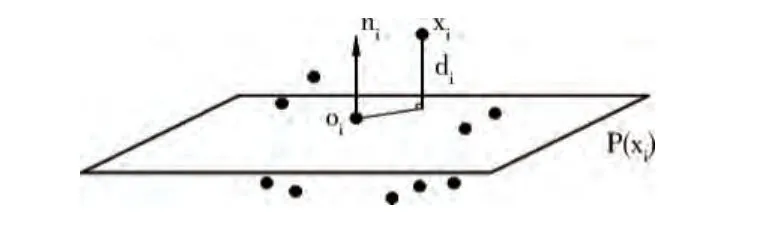
图2 切平面距离计算

为标记平坦点和非平坦点，根据模型几何形状设定距离阈值Ωd，一般取经验值Ωd＝0.1。如果di＜Ωd，则该点为平坦点，否则为非平坦点。确定出所有点的类型后，用长度为N的一维数组FP记录其类型，平坦点标记为1，非平坦点标记为0。在此基础上再划分出平坦区域和非平坦区域。

3 三角网格质量评价与修正

三角网格和网格转化过程中的局部混合网格的质量参差不齐，而修正网格结构 （连通性）会相应提高网格的质量，因此在网格转化前和网格转化过程中，以及局部后处理和全局后处理时，将会频繁对基本网格进行修正。

3.1 网格质量评价

为了使背景三角网格的单元大小分布与度量规范相兼容，在三角网格所有节点处定义曲面度量张量［9］M。

在3D 空间，度量张量是一个对称正定矩阵M3D，如Det（M3D）＞0，同时矩阵M3D的特征对 （gi，λi） （i＝1，2，3）定义网格的主要延伸方向和节点空间。通过利用M3D，规范化空间中的基本矢量dε和3D 空间中对应矢量dx 之间的长度尺度变换为

在参数空间中，通过使用等式 （x，y，z）T＝r（u，v），把节点密度的用户规范效果M3D和曲面映射结合在一起的2×2曲面度量张量M 可以定义为

假设参数空间中存在两点p1（u1，v1）和p2（u2，v2），则相对于M 两点p1和p2间的距离定义为

通过利用度量规范描述曲面映射 （参数化），三角化和四边形转化方法都可以被应用到范围广泛的曲面，包括那些具有快速变化的曲面偏导数和奇异点。

若存在△P1P2P3，由长度尺度测量和曲面度量张量，并根据式 （3）和式 （4），它的形状质量评价如下

式中

在式（7）中，Mi是Pi点处的曲面度量，Det（M）是矩阵M 的行列式。注意等式 （6）中的形状质量仅仅取决于三角形的形状变形（相对于度量张量），而与边长偏差没有关系。由于任何尺寸等边三角形的最大值都等于1。鉴于此，使用结合形状和尺寸的参数来表示三角单元总体质量

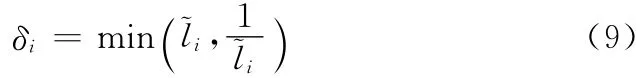
本文使用结合形状和尺寸的参数珘μ 对三角形总体质量进行评价，这比使用α 质量因子更能在质量参差不齐的三角单元中分辨出不满足要求的三角单元。

3.2 修正策略

完成三角网格质量评价后，采用以下4种网格修正策略对不满足要求的网格进行修正。

（1）棱交换：用连接相对节点的新棱替换相邻两单元原有共有棱，如图3 （a）所示。对于一个有效的交换操作，在度量空间和参数空间中两对新形成的角度和都应小1800，如图3 （b）所示。

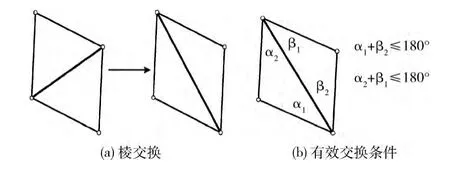
图3 棱交换

（2）棱塌陷（单元删除）：在棱塌陷操作中，把满足一定条件的两个单元共有棱删除，共有棱两端的节点合并成一个节点。因此与该棱相邻的两个单元同时被删除。如图4所示。

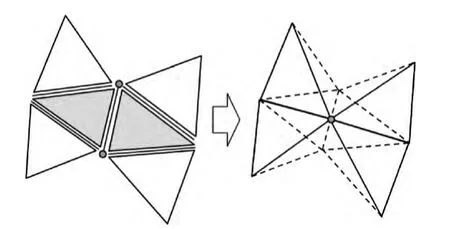
图4 棱塌陷 （单元删除）

（3）棱分割：棱分割过程中，在相邻两单元共有棱的中点处裂开，两个相邻单元将会被分为4个单元，如图5所示。

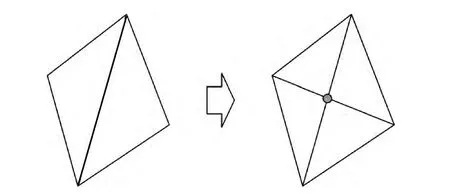
图5 棱分割

（4）节点删除：当一个节点被3个或4个三角形单元围绕时，可以执行节点删除操作。如果节点被3个三角形包围，如图6 （a）所示，它们将合并为一个三角单元；对于节点由4 个三角形单元围绕的情况，如图6 （b）所示，将生成一条新棱，且这条棱为四边形长度最短的对角线。

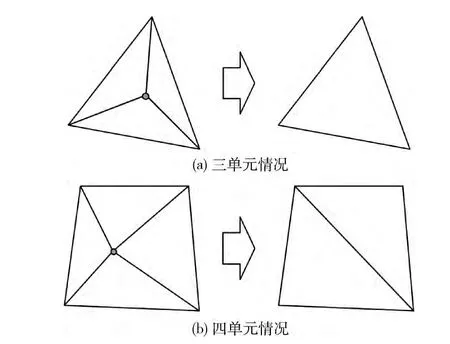
图6 节点删除

为了改善三角网格质量，利用以上4种网格修正方法优化背景三角单元。首先遍历计算三角形网格中每一个三角形单元的形状和尺寸参数，若不在规定的阈值Ω 范围内 （0.3≤Ω≤0.7），可根据每一个不满足质量要求的三角形单元的具体情况选择合适修正策略对其进行处理。

4 基段选择算法

在四边形网格形成过程中，基段决定新单元的位置以及合并前沿前进方向。四边形质量优劣以及转化过程是否顺利进行取决于是否选择最优基段。Q－Morph根据每一个前沿段的H 值和两个前沿额角选择最优基段 （优先权给予具有较小的H 值和额角接近理想值θrect＝1350的前沿段），前沿段和额角如图 （1）所示。利用这种算法选择基段之前需要知道每个前沿段的H 值和额角，并比较各前沿段H 值的大小，判断额角是否接近理想值。因为使用该算法确定基段需要计算、比较两个值，所以选择程序复杂，花费时间多。并且在四边形网格形成过程中没有考虑不同区域几何形状的差异，仅使用一种基段选择方法。除此之外，QMorph使用的额角计算公式仅适用于常规三角网格，而对于各项异性或几何质量较差的三角网格，计算精度不高。本文算法思想是首先计算出每个前沿段两端节点处的额角值，然后依据给定的判别条件确定每个前沿段的状态；在平坦区域，当前沿段状态相同时，计算每个前沿段的H值，选择H 值最大的前沿段作为基段；当前沿段状态不相同时，则选择状态级别高的前沿段作为基段；对于不平坦区域，选择长度小于cHmin（1.5≤c≤2）且状态级别相对高的前沿段为基段。由于前沿段状态不同是大概率事件，因此算法减少了计算量，提高了算法运行效率。此外，本文算法采用适用于各向异性三角网格的额角计算公式，能够明显提高额角的计算精度。

4.1 前沿段H 值和额角

第i个前沿段的H 值计算公式如式 （10）所示

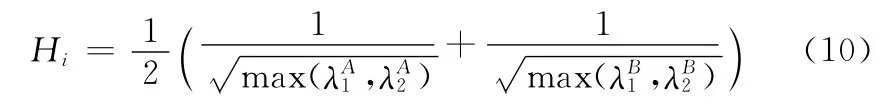
式中：λAk和λBk，k＝1，2分别是节点A 和节点B处度量张量M 的特征值 （参考3.1）。

根据度量张量M 和等式 （5），额角的计算如下

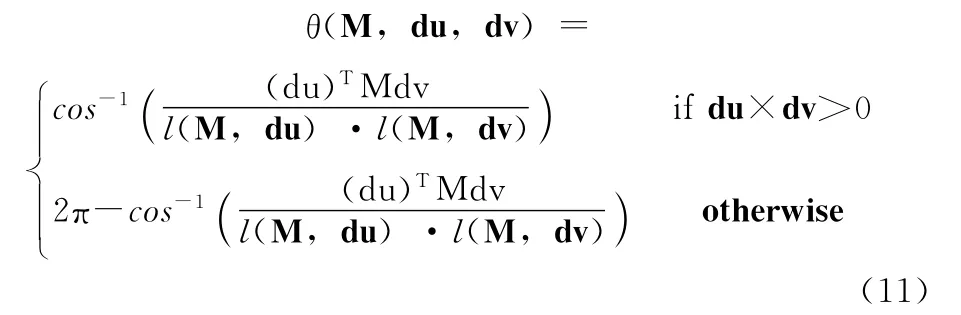
式中：du，dv——无穷小矢量。

4.2 前沿段状态和分级

前沿段在两端节点处的额角值决定这个前沿段的状态，额角计算参考式（11）。对合并前沿中的每一段根据它的状态进行分级，得到的分级结果影响选择哪一个前沿段作为基段。

由于一条前沿段状态是根据前沿段两个端节点处的额角值确定的，因此前沿段状态由两个要素进行定义：一个表示左节点位，另一个表示右节点位。如果一个节点处的额角值小于特定阈值Φ （通常Φ＝1350），则该节点位设置为1，否则设置为0。每一个前沿段状态分类存放在4种状态列表中的一个，前沿段的4种状态如图7所示，图中当前前沿段用粗实线显示。

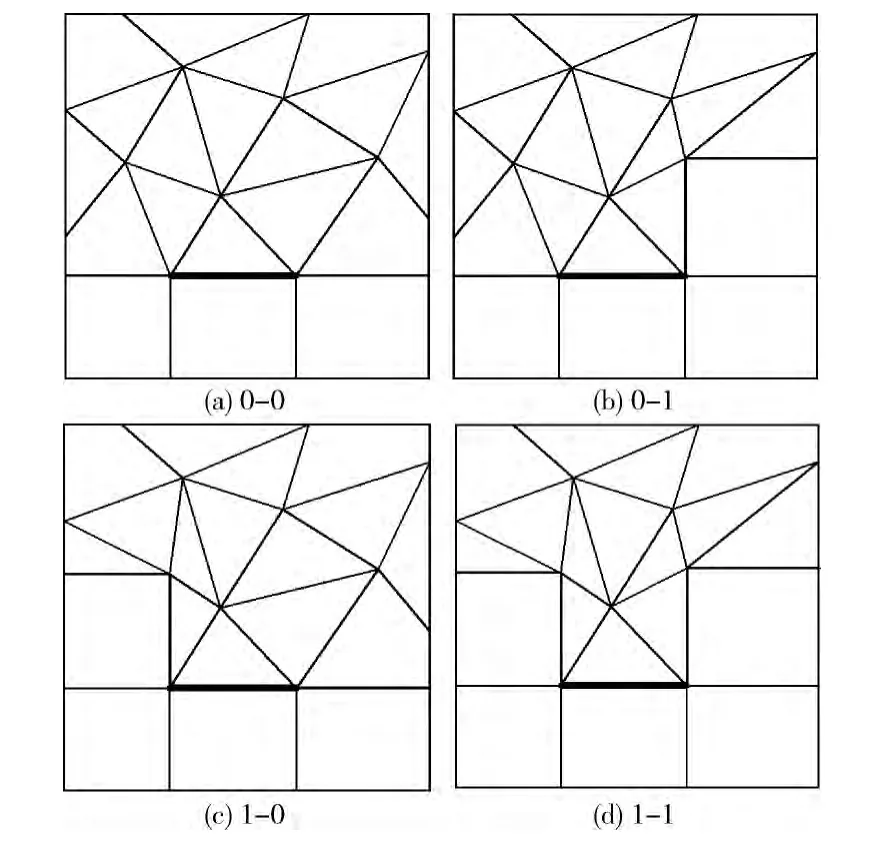
图7 前沿段状态

根据状态对前沿段分级有两个目的：一是明确处理前沿段的优先次序。状态为1－1的前沿段给予第一优先权，然后依次是状态为0－1、1－0和0－0的前沿段；二是为定义侧边做准备，因为通常定义至少一端已设置状态位的棱为待形成四边形的侧边。

4.3 基段选择算法流程

（1）通过计算确定合并前沿中每个前沿段两端节点处的额角值，判定出它们的状态；

（2）判断合并前沿是否在平坦区，若在平坦区，继续向下进行，否则转到 （7）；

（3）若前沿段状态相同，计算每个前沿段的H 值，选择H 值最大的前沿段作为基段，否则转到 （8）；

（4）把作为基段的前沿段从前沿列表中删除；

（5）在基段基础上生成四边形后，若前沿列表非空，把新形成的前沿段添加到前沿列表中，同时更新与新四边形相邻前沿段的状态以及相邻三角网格的结构，然后返回（1），否则转到 （6）；

（6）若前沿段列表为空，算法结束；

（7）若在不平坦区，选择长度小于cHmin且状态级别相对高的前沿段为基段，然后转到 （4）；

（8）若前沿段状态不同，选择等级高的前沿段作为基段，并转到 （4）。

根据算法选择出基段之后，由以下步骤构建一个新四边形单元：①确定待生成四边形的左右侧边；②执行顶边再生操作，连接两个侧边的顶节点，生成顶边；③合并四条边围成的闭合区域内所有三角形，形成一个四边形单元。

把三角网格转化为四边形网格后，执行全局后处理。应用一组标准网格改进程序和网格光顺程序［10］，进一步提升四边形网格质量。转化完成后形成的四边形网格与三角网格自由的拓扑连接关系不同，具有规则的连接，网格边沿主曲率方向分布，能自然表现出模具几何形状的变化［11］。

5 实 例

以某汽车模具为例进行了实例验证，实验结果如图8、图9所示。其中图8 （a）是模具点云经三角化和优化后得到的三角网格模型，它有156886个三角形；图8 （c）是转化后生成的四边形网格模型，四边形数为70229 个，图中显示出模型曲面处的网格密度大，平坦区域网格密度小，并且生成的四边形单元匀称，整个模型很好保持了模具的特征，达到了不同区域分别采用相适宜方法转化的效果。

图8 模具点云网格化

图9 模具点云曲面拟合

表1是Q－Morph改进算法与本文算法在转化速率和网格质量方面的比较。比较结果表明本文算法达到了预期效果。表中质差率为质量差的四边形数占总数的百分比。

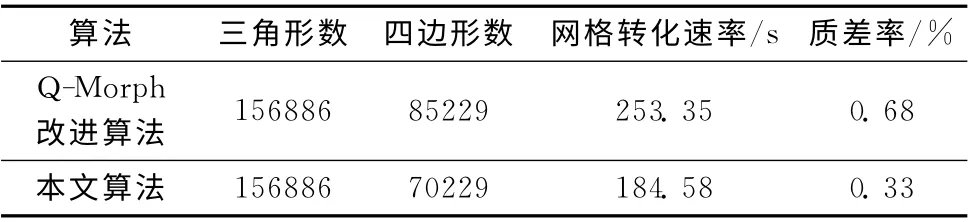
表1 两种算法的数据比较

6 结束语

本文在优化三角网格后，使用基于区域划分的基段选择算法确定待形成四边形基段，其优势有以下3点：

（1）采用长度尺度测量和曲面度量张量相结合的三角形质量评价准则，可以更准确检测出质量差的三角形单元。

（2）使用新额角计算公式，提高了计算精度，从而更准确对前沿段进行分级；

（3）简化选择基段的判断条件，并能够根据不同区域采用与之相适宜的基段选择方法，因此提高了网格转化效率以及增大了选择出最优基段的概率。

实例验证在优化三角网格的基础上，使用本文算法提高了四边形网格生成效率，明显改善了最终生成的四边形网格质量，保证了随后进行的曲面重构效果，并为下一步模型改进、缺损模具修复以及数控加工创造了有利条件。

此外，算法还存在不足之处：平坦区网格密度要求尽可能小，但是在平坦区由于没有结合前沿段的级别和长度选择最优基段，会造成平坦区网格没有达到最理想的密度。如果两者都考虑，会大幅增大计算量，也会对网格质量产生一定影响。

［1］Park C，Noh JS，Jang IS，et al.A new automated scheme of quadrilateral mesh generation for randomly distributed line constraints ［J］.Computer－Aided Design，2007，39 （4）：258－267.

［2］LIU Jing，NIE Yufeng，SU Shaopu.Indirect method of quadrilateral mesh generation ［J］.Computer Engineering and Application，2010，46 （2）：44－47 （in Chinese）. ［刘晶，聂玉峰，苏少普.四边形网格间接生成方法 ［J］.计算机工程与应用，2010，46 （2）：44－47.］

［3］Lo SH.Delaunay triangulation of nonuniform point distributions by means of multigrid insertion ［J］.Finite Elements in Analysis and Design，2013，63：8－22.

［4］CHEN Jianjun，ZHEN Jianjing，JI Tingwei，et al.Advancing front quadrilateral surface mesh generation ［J］.Chinese Journal of Computational Mechanics，2011，28 （5）：779－784 （in Chinese）.［陈建军，郑建靖，季廷炜，等.前沿推进曲面四边形网 格 生 成 算 法 ［J］.计 算 力 学 学 报，2011，28 （5）：779－784.］

［5］CHEN Yang，CUI Hanguo，LIU Jianxin，et al.Improved algorithm for advancing front growth in quadrilateral mesh generation ［J］.Computer Engineering，2011，37 （9）：291－293 （in Chinese）.［陈阳，崔汉国，刘健鑫，等.四边形网格生成中的前沿边生长改进算法 ［J］.计算机工程，2011，37（9）：291－293.］

［6］GUO Jin，YUAN Jianying，CHEN Xiaoning.Algorithm for removing redundancy points based on multiview geometric［J］.Computer Engineering ＆Design，2014，35 （3）：958－962 （in Chinese）.［郭进，袁建英，陈小宁.基于多视几何的重叠点云 删 除 算 法 ［J］.计 算 机 工 程 与 设 计，2014，35 （3）：958－962.］

［7］DAI Xing，CUI Hanguo，HU Huaiyu.Fast data point simplification algorithm based on curvature character［J］.Journal of Computer Applications，2009，29 （11）：3030－3032 （in Chinese）.［代星，崔汉国，胡怀宇.基于曲率特征的点云快速简化算法 ［J］.计算机应用，2009，29 （11）：3030－3032.］

［8］Connor M，Kumar P.Fast construction of K－nearest neighbor graphs for point clouds ［J］.IEEE Transactions on Visualization ＆Computer Graphics，2010，16 （4）：599－608.

［9］Xie Hehu，Yin Xiaobo.Metric tensors for the interpolation error and its gradient in Lp norm ［J］.Journal of Computational Physics，2014，256：543－562.

［10］HU Shimin，LAI Yukun，YANG Yongliang.A curvature flow based fairing algorithm of quad－dominant meshes ［J］.Chinese Journal of Computers，2008，31 （9）：1622－1628 （in Chinese）.［胡事民，来煜坤，杨永亮.基于曲率流的四边形主导网格的光顺方法 ［J］.计算机学报，2008，31 （9）：1622－1628.］

［11］ZHU Weipeng，GAO Chengying，LUO Xiaonan.Global anisotropic quad－dominant remeshing ［J］.Journal of Soft，2012，23 （5）：1305－1314 （in Chinese）.［朱为鹏，高成英，罗笑男.全局各向异性四边形主导网格重建方法 ［J］.软件学报，2012，23 （5）：1305－1314.］