基于随机响应面法考虑随机变量相关性的概率潮流计算

郭小璇，龚仁喜，鲍海波

（ 1. 广西大学 电气工程学院， 广西 南宁 530004； 2. 广西电网电力科学研究院， 广西 南宁 530023）

为了应对能源危机和不断增长的负荷需求，缓解资源环境等诸多方面的压力，实现智能电网电源侧的清洁化，电力系统必然需要大规模的风电以集中或者分布式发电的形式接入[1-2]。 风电场输出功率受风速等自然条件的影响， 具有随机性和波动性。风电的大量接入势必会对电力系统的潮流分布带来影响。 传统确定性的潮流分析方法[3-7]重视系统某一特定状态的潮流分布，而没有考虑特定状态的出现概率，结果往往偏于乐观，难以全面描述系统的运行状况和潮流分布。随机潮流分析技术[8-15]可以更深刻地揭示系统运行状况，为系统安全运行及控制提供更完整的信息，是解决所存在问题的有效方法和手段。

随机潮流技术是由Borkowska在1974年提出的[8]，运用概率统计方法处理电力系统运行中的随机变化因素，给出系统的节点电压、支路潮流等概率分布情况。 现今，常用的随机潮流方法主要有模拟法[9]、解析法[10-16]和点估计法[17-18]等。 模拟法仿真次数多、耗时长，限制了其实际应用。解析法可考虑负荷波动、发电机和线路故障等多种随机因素，可以一次求出支路潮流和节点电压等状态变量的期望、方差等信息， 在速度和精度上都取得了很好效果，但其需要复杂的公式推导。点估计法是近年来比较常用的概率分析方法，已在概率潮流、概率最优潮流、 电压稳定概率评估等领域取得了很好的应用效果。

现有含风电场电力系统随机潮流计算[16-20]，往往假设各节点之间的节点负荷相互独立，各风电场的输出功率也相互独立。 但事实上，各风电场地理位置可能非常靠近， 其风速具有较强的相关性，从而各风电场的输出功率也具有较强的相关性。 若不考虑相关性， 可能会对系统潮流变化的估计不足，造成系统运行风险的低估。 文献[19]中采用自回归滑动平均模型和时移技术的方法，研究了风速相关性对系统潮流分布的影响，但没有给出考虑风速相关性的随机潮流计算方法。 文献[18]研究了结合正交变换技术的扩展的点估计方法，并将其应用于求解含风速相关的风电场电力系统潮流计算中。

为了准确描述风电场输出功率随机特性，分析风电接入对系统潮流分布的影响，本文提出了基于随机响应面法[22-26]（ SRSM，Stochastic Response Surface Method）的电力系统随机潮流计算方法。将随机潮流分析转化为确定性潮流分析，用传统潮流计算方法加以求解，从而得到各潮流状态变量（ 节点电压、支路功率等）的统计特征值和概率分布。 考虑到地理位置靠近的多个风电场之间，风速具有较强的相关性， 进一步采用正交变换技术处理相关的风速。IEEE-14和IEEE-118系统的计算结果表明， 该方法与蒙特卡洛方法（ MC， Monte Carlo method）相比，具有较高的计算精度和较小的计算量。

1 含风电场的随机潮流模型

1.1 风电场随机模型

风电场的输出功率取决于风电场内各台风电机组的输出功率，而风电机组的发电功率随着风速的波动而变化，它与风速之间的关系可表示为[13-14]：

风电场输出功率为：

式中，NW是风电场的风电机组台数。

大量实测数据表明，一个地区的风速近似服从双参数威布尔（ Weibull）分布，风电场风速v的概率密度函数表示为：

式中，K为威布尔分布的分布形状参数；C为尺度参数。

经实测，大部分时间内风速维持在切入风速和额定风速之间，可近似认为Pr与风速v成一次函数关系，根据式（ 3），确定风机输出有功功率PWg的概率密度函数：

结合式（ 2）即得到风电场输出有功功率PW的概率密度函数。

目前，我国大型风电场中一般采用的是异步发电机，其在发出有功功率的同时从系统吸收无功功率。 假定通过电容器自动投切，可使风电机组功率因数恒定不变，风电场吸收无功功率为：

式中，θW为风电场的风机功率因数角。

1.2 节点负荷模型

由于电力系统预测、测量等方面的误差，未来某一时刻的负荷预测结果，即系统中各节点负荷功率可以作为随机变量。

各节点负荷随机性，有功功率的随机分布可以用以μ为均值，σ为标准差的正态分布表示。 PL的概率密度函数为：

假设各节点负荷功率因数保持不变，节点无功功率可由有功PL确定。

1.3 含风电场电力系统潮流方程

风电场可简化处理为PQ节点，将其输出功率考虑到潮流计算中建立如下的潮流方程：

式中，SPV和SPQ分别为系统PV和PQ节点集合；PGi和QRi为节点i传统电源发出的有功、无功功率；PWi和QWi为节点i处风电场发出的有功、 无功功率；PLi和QLi为节点i负荷有功、无功功率。Vi和δi为节点i电压幅值和相角；Yij为节点导纳矩阵元素，αij为节点导纳矩阵相应元素的相角，δij=δi－δj－αij。

2 随机响应面法

SRSM基本原理[22]是在已知输入随机变量概率分布的基础上， 将输出响应近似表示为关于已知参数的混沌多项式函数， 进行少量仿真确定多项式的未知系数，进而得到所估计的输出响应的概率分布。在本质上，SRSM与MC方法一样， 属于模拟类方法，保持着模拟类方法可并行的计算优势， 其所需的仿真次数比MC方法更少，可以在减小仿真次数的同时保持估计的精度。

SRSM的一般计算流程如图1中示。SRSM概率分析的基本步骤为：

1） 输入变量标准化，将输入随机变量用一组标准随机变量的函数关系表示。

2） 输出响应标准化，将待求输出响应用标准随机变量为自变量的Hermite混沌多项式表示。

3） 样本点模型计算，选择适当的采样点，进行样本点的模型计算，确定混沌多项式中的待定参数，计算输出响应概率分布的特征参数。

图1 SRSM基本流程Fig. 1 Flow chart of SRSM

随机潮流计算可看作“ 黑箱”，黑箱的模型为F，其待求的状态变量是模型F的输出响应Y=（ Y1，Y2，…，Ym）T，各风电场风速和部分不确定的节点负荷功率是模型F的输入随机变量X=（ X1，X2，…，Xn）T，模型F可表达为：

基于SRSM的随机潮流计算问题，就是分析模型式（ 8）的响应Y的概率分布，其过程为：

第一步，选择适当的标准输入变量，本文选择标准正态分布的随机变量ξ=（ ξ1，ξ2，…，ξn）作为标准随机变量，输入变量X可由ξ表示为：

式中，F－1（·）为输入随机变量x的累积概率分布函数的反函数；Φ（·）为标准正态分布的累积概率分布函数。

满足威布尔分布的风速v，用ξ标准化为：

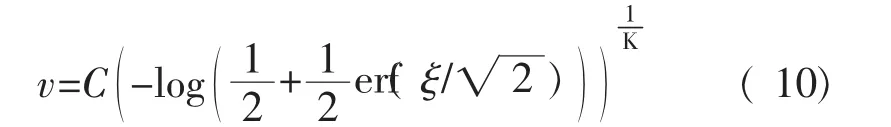
满足正态分布的部分不确定节点负荷，可用ξ标准化为：

式中，θL为节点负荷的功率因数角。

第二步，将输出响应Y用关于ξ的Hermite混沌多项式表达：

式中，a0、ai1、ai1i2等为待定系数；Hm（ ξi1，ξi2，…）为ξ的m阶Hermite多项式，其计算公式为：

混沌多项式（ 3）中待定系数的个数为

Hermite多项式的阶数越高，m越大时，混沌多项式（ 12）对输出响应Y模拟的精度越高，但同时待定系数的个数也越多。 大量的实际测试表明，当m≥3时，增加阶数m所提高精度的影响已经不明显，本文采用二阶混沌多项式：

第三步，选择Na个样本点，计算各样本点潮流，确定式（ 12）的待定系数。 样本点选取原则是：选取0点和m+1阶Hermit多项式的根作为采样点， 每个标准正态随机变量ξ都取为0或者m+1阶Hermite多项式的根。 按此原则，可供选择的采样点个数为：

实际中，Nc垌Na。 因此，应选取高概率区域的样本点，且关于原点对称布置采样点[25]。为了平衡每个样本点对输出响应的影响，选择采样点个数应大于Na，一般选择2Na个。

若有2个标准随机输入变量（ ξ1，ξ2）， 输出响应Y=（ Y1，Y2）T， 它们的二阶混沌多项式的待定系数分别为a=（ a0，a1，…，a5）T和b=（ b0，b1，…，b5）T。 按采样点选取原则，选取12个采样点（ ξ1，1，ξ2，1），（ ξ1，2，ξ2，2），…，（ ξ1，10，ξ2，10）， 计算各样本点输出响应Y1，1， …Y1，12和Y2，1，…Y2，12。 所需求解的线性方程组表示为：

3 随机变量相关性处理

3.1 正交变换技术

采用正交变换技术[18，27]，将原先相关的输入随机变量线性变换为不相关随机变量。 由n个随机变量组成的随机向量X=（ x1，x2，…，xn）T，各随机变量均值μ=（ μ1，μ2，…，μn）T，方差σ=（ σ1，σ2，…，σn）T，随机变量xi和xj之间相关系数为ρij，协方差矩阵：

CX为对称矩阵，存在正交变换矩阵P，通过式（ 9）变换将X转化为不相关的随机变量Z：

Z的协方差矩阵CZ为单位矩阵，即CZ=I。

实际工程中，CX一般是对称正定矩阵， 可通过求解LLT=CX对其进行Cholesky解耦。

根据式（ 8）可以推导：

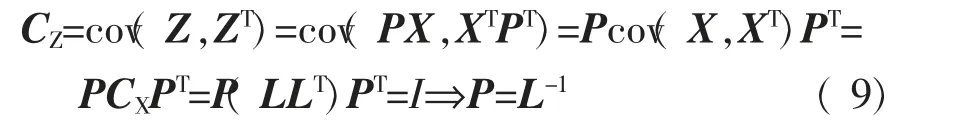
用SRSM概率分析时，需将相关的输入随机变量X变换为不相关的Z，再进行标准化。

3.2 结合正交变换技术的SRSM

随机潮流计算模型的输入随机变量X为各风电场风速vi及部分不确定的节点负荷功率PLi和QLi。 由于各风电场风速具有相关性，X是相关的随机变量。基于SRSM的随机潮流计算步骤为：

1） 对X的协方差矩阵CX进行Cholesky解耦，得到变换矩阵P。

2） 通过式（ 9）将X转换为不相关的随机变量Z，将Z用标准随机变量ξ表示。

3） 将潮流方程的状态变量以关于ξ 的二阶Hermite混沌多项式表示。

4） 选择ξ的采样点，先确定Z样本点，然后通过X=B－1Z变换得到X样本点，即得到各样本点的vi、PLi、QLi。

5） 应用Newton法求解各样本点的潮流。

6） 确定3）步中二阶混沌多项式的待定系数，得到所需潮流方程状态变量的概率分布。

4 算例分析

4.1 系统概况

在Matlab R2010b平台编写程序实现本文方法，所用计算机为IBM-PC兼容机，CPU主频为2.19 GHz×2，内存为3 GB。 本文接入测试系统的各风电场主要数据，如表1所示。

在IEEE-14系统节点10接入风电场1，风电场额定输出功率为30 MW，占所有发电机总有功出力的11.54%； 在IEEE-118系统的节点23、39、114接入风电场2、3、4，风电场总额定输出功率为580 MW，占所有发电机总有功出力的15.81%。 接入电网的风电比例，符合当前系统实际。 假设不确定的节点负荷有功，服从以当前负荷有功为均值，标准差为5%均值的正态分布。

表1 各风电场参数Tab. 1 Parameters of wind farms

4.2 算法有效性测试

为验证SRSM方法的有效性， 应用SRSM计算IEEE-14节点系统的随机潮流， 并与10 000次仿真的蒙特卡洛方法计算结果对比。 表2和表3中分别为各节点的电压幅值、相角的期望和标准差，表4和表5为各条线路的有功无功的期望和标准差。 基于SRSM的随机潮流计算结果，与蒙特卡洛方法差别很小，均值和标准差的最大误差都不超过3%，表明其具有可靠的计算精度。

IEEE-14系统中， 节点1处发电机承担调频任务。 图2为节点1发电机有功出力的概率密度曲线。本文方法的结果，与蒙特卡洛方法吻合度很好。

4.3 风速相关性对随机潮流的影响

电力系统中风电场地理位置可能会很靠近，其风速一般具有较强的相关性，各风电场的输出功率也具有较强相关性。 根据各风电场风速相关性大小，分以下3种情况，计算IEEE-118系统的随机潮流。

表3 IEEE-14节点系统电压相角的期望和标准差Tab. 3 Expectation and standard deviation of voltage phase angle for IEEE-14 system

表4 IEEE-14节点系统各线路有功功率的期望和标准差Tab. 4 Expectation and standard deviation of line active powers for IEEE-14 system

情况1：风速不相关，相关系数ρW=0；

情况2：风速中度相关，ρW=0.4；

情况3：风速高度相关，ρW=0.8。

表5 IEEE-14节点系统各线路无功功率的期望和标准差Tab. 5 Expectation and standard deviation of line reactive powers for IEEE-14 system

图2 平衡节点有功功率的概率密度曲线Fig. 2 Probability density distribution of active power of slack node

表6为不同情况下， 风电场接入节点和邻近节点的电压幅值的波动。 表7为不同情况下，部分线路传输功率波动。 结果表明，风速相关性对概率潮流的计算结果有较大影响。 考虑风速相关性时，节点电压和线路传输功率的波动范围较大，电压越限和线路传输功率越限的概率也较大。

表6中，与情况1相比，情况3节点21电压越限的概率从0.570 0增大至0.588 6，增大了3.25%。

表7中，与情况1相比，情况3下大部分线路的传输功率越限概率都有所增加。 图3和图4中是不同情况下，线路38-65和65-68传输功率的累积概率曲线对比。 同样可以看出，风速相关性较大的情况3，线路功率的分布范围较大。

表6 不同情况下部分节点电压的波动Tab. 6 Voltage fluctuation at some nodes under different conditions

表7 不同情况下部分线路传输功率的波动Tab. 7 Line transmission power fluctuation under different conditions

图3 线路38-65传输功率累积概率曲线比较Fig. 3 Probability density distribution of active power of slack node under different conditions for line 38-65

图4 线路65-68传输功率累积概率曲线比较Fig. 4 Probability density distribution of active power of slack node under different conditions for line 65-68

表8中给出了不同情况下， 电压越限概率大于0.005的节点个数和传输功率越限概率大于0.005的线路数。 显然，风电场风速较高相关性时，系统中潜在危险的节点和线路数明显增多。

表8 线路传输功率越限和节点电压越限对比Tab. 8 Contrast of line transmission power fluctuation beyond limits and node voltage beyond limits

风电场之间风电场风速相关系数变化，平衡发电机有功出力和各风电场总有功出力的均值变化趋势如图5所示。 随着风速相关系数的增大，风电场总有功出力均值先增大后减小，平衡发电机有功出力均值先减小后增大。 当风速相关系数为0.6左右时，风电场总有功出力最大约为260 MW，平衡发电机有功出力最小，约为240 MW。

图5 发电机有功出力均值变化Fig. 5 Variation of active power mean values with wind speed correlation coefficient for generators

图6中为平衡发电机有功出力和各风电场总有功出力的标准差变化趋势。 风速相关系数的不断变大，各风电场总有功出力的标准差变大，与此同时，平衡发电机有功出力的标准差也随之变大。 可见，位置比较靠近、风速相关的风电场并网，对于平衡发电机的调节能力的要求更高。

图6 发电机有功出力标准差变化Fig. 6 Variation of active power standard deviation wind speed correlation coefficient for generators

对于IEEE-118系统， 基于MC的随机潮流运行一次时间为56.892 4 s， 基于SRSM的随机潮流运行一次的时间是0.613 6 s， 仅约为MC方法的百分之一，其计算效率具有明显优势。

5 结论

本文考虑了风电场出力变化和节点负荷波动的随机因素，提出了一种基于SRSM的随机潮流计算方法。 研究了风电场之间风速的相关性，利用正交变换技术处理相关的风速，分析了其对随机潮流分布的影响。 IEEE-14和IEEE-118节点系统的计算结果表明，该方法计算量少，计算效率高，结果准确。由于SRSM属于模拟类方法， 具有可并行的计算优势，可以将其与并行计算技术结合，推广应用于电力系统其他概率分析问题的求解。

[1] 王承煦，张源.风力发电[M]. 北京：中国电力出版社，2003.

[2] 陈树勇， 宋书芳， 李兰欣， 等. 智能电网技术综述[J]. 电网技术， 2009， 33（ 8）： 1-7.CHEN Shuyong， SONG Shufang， LI Lanxin， et al. Survey on smart grid technology[J]. Power System Technology，2009， 33（ 8）： 1-7（ in Chinese）.

[3] 吴凯槟， 彭旭东， 杨秀芳， 等. 分布式能源面临重大发展机遇[J]. 节能技术， 2013， 31（ 5）： 437-441.WU Kaibin， PENG Xudong， YANG Xiufang， et al. Distributed energy faces significant development opportunities[J].Energy Conservation Technology， 2013， 31（ 5）： 437-441（ in Chinese）.

[4] 张力， 肖立鑫， 杨楠， 等. 考虑风电大规模接入的电力系统调峰平衡分析[J]. 陕西电力， 2014， 42（ 6）： 12-15.ZHANG Li， XIAO Lixin， YANG Nan， et al. Evaluation on peak load balance of power system accessed by largescale wind power[J]. Shaanxi Electric Power， 2014， 42（ 6）： 12-15（ in Chinese）.

[5] 王锡凡. 现代电力系统分析[M]. 北京： 科学出版社，2003.

[6] TINNEY W F，HART C E.Power flow solution by newton’s method[J]. IEEE Trans on Power Apparatus and Systems，1970， 86（ 11）： 1449-1460.

[7] 杨跃光， 刘璇. 一种改进的Newton算法在电力系统潮流计算中的研究与应用[J]. 陕西电力， 2011， 39（ 10）： 4-6.YANG Yueguang， LIU Xuan. Research and application of im proved newton algorithm for power flow calculation in power system[J]. Shaanxi Electric Power， 2011， 39（ 10）：4-6.

[8] BORKOWSKA B. Probability load flow[J]. IEEE Trans. on Power Apparatus and Systems， 1974， 93（ 3）： 752-759.

[9] 丁明， 李生虎， 黄凯. 基于蒙特卡洛模拟的概率潮流计算[J]. 电网技术， 2001， 25（ 11）： 10-14.DING Ming， LI Shenghu， HUANG Kai. Probabilistic load flow analysis based on monte-carlo simulation[J]. Power System Technology， 2001， 25（ 11）： 10-14（ in Chinese）.

[10] 王锡凡， 王秀丽. 电力系统随机潮流[J]. 西安交通大学学报， 1988， 22（ 2）： 87-97.WANG Xifan， WANG Xiuli. Probability load flow analysis in power systems[J]. Journal of Xi’an Jiaotong University，1988， 22（ 2）： 87-97（ in Chinese）.

[11] 胡 泽 春， 王 锡 凡， 张 显， 等. 考 虑 线 路 故 障 的 随 机 潮流[J]. 中国电机工程学报， 2005， 25（ 24）： 26-33.HU Zechun， WANG Xifan， ZHANG Xian， et al. Probability load flow method considering branch outages[J].Proceeding of CSEE，2005，25（ 24）：26-33（ in Chinese）.

[12] 胡泽春， 王锡凡. 基于半不变量法德随机潮流误差分析[J]. 电网技术， 2009， 33（ 18）： 32-37.HU Zechun， WANG Xifan. Error analysis of probability load flow based on cumulant method[J]. Power System Technology， 2009， 33（ 18）： 32-37（ in Chinese）.

[13] 董雷， 程卫东， 杨以涵. 含风电场的电力系统概率潮流计算[J]. 电网技术， 2009， 33（ 16）： 87-91.DONG Lei， CHENG Weidong， YANG Yihan. Probabilistic load flow calculation for power grid containing wind farms[J]. Power System Technology， 2009， 33（ 16）： 87-91（ in Chinese）.

[14] 王成山，郑海峰，谢莹华，等.计及分布式发电的配电系统随机潮流计算[J]. 电力系统自动化，2005，29（ 24）：39-44.WANG Chengshan， ZHENG Haifeng， XIE Yinghua， et al.Probabilistic power flow containing distributed generation in distribution system[J]. Automation of Electric Power Systems， 2005， 29（ 24）： 39-44（ in Chinese）.

[15] 刘怡芳， 张步涵， 李俊芳， 等. 考虑电网静态安全风险的随机潮流计算[J]. 中国电机工程学报，2011，31（ 1）：59-64.LIU Yifang， ZHANG Buhan， LI Junfang， et al. Probabiltiy load flow algorithm considering static security risk of the power system[J]. Proceeding of CSEE， 2011， 31（ 1）： 59-64（ in Chinese）.

[16] USAOLA J. Probabilistic load flow in systems with wind generation[J]. IET Generation，Transmission&Distribution，2009， 3（ 12）： 1031-1041.

[17] MORALES J M， JUAN P R. Point estimate schemes to solve the probabilistic power flow[J]. IEEE Trans on Power System， 2007， 22（ 4）： 1594-1601.

[18] MORALES J M， BARINGO L， CONEJO A J， et al.Probabilistic power flow with correlated wind sources[J].IEE Generation，Transmission&Distribution，2010，4（ 5）：641-651.

[19] 夏天， 杨京燕， 杨媛媛， 等. 计及电压崩溃风险的风电并网系统多目标无功优化[J]. 陕西电力， 2012，40（ 7）：8-13.XIA Tian，YANG Jingyan，YANG Yuanyuan，et al.Multiobj ective reactive power optimization in wind power integrated system considering the risk of voltage collaps[J].Shaanxi Electric Power，2012， 40（ 7）：8-13（ in Chinese）.

[20] 胡斌. 考虑大规模风电并网的电力系统旋转备用容量优化模型[J]. 陕西电力， 2014， 42（ 5）： 22-26.HU Bin. Optimal spinning reserve capacity model of power system considering large scale wind power[J]. Shaanxi Electric Power， 2014， 42（ 5）： 22-26（ in Chinese）.

[21] 范荣奇， 陈金富， 段献忠， 等. 风速相关性对概率潮流计算的影响分析[J]. 电力系统自动化，2011，35（ 4）：18-22.FAN Rongqi， CHEN Jinfu， DUAN Xianzhong， et al.Impact of wind speed correlation on probabilistic power flow[J]. Automation of Electric Power Systems， 2011， 35（ 4）： 18-22（ in Chinese）.

[22] LSUKAPALLIS S， ROY A， GEORGOPOULOS P G.Stochastic response surface methods for uncertainty propagation: application to environmental and biological systems[J]. Risk Analysis， 1998， 18（ 3）： 351-363.

[23] 韩冬， 贺仁睦， 马进， 等. 基于随机响应面法的动态仿真不确定性分析[J]. 电力系统自动化， 2008，32（ 20）：11-14.HAN Dong，HE Renmu，MA Jin，et al.Quantitative uncertainty analysis for power system dynamic simulation based on stochastic response surface method[J]. Automation of Electric Power Systems，2008，32（ 20）：11-14（ in Chinese）.

[24] 韩冬， 马进， 贺仁睦， 等. 电力系统时域仿真的动态一致性检验[J]. 电力系统自动化， 2010， 34（ 16）： 29-33.HAN Dong， MA Jin， HE Renmu， et al. Dynamic consistency test for power system time-domain simulation[J].Automation of Electric Power Systems， 2010， 34（ 16）：29-33（ in Chinese）.

[25] 鲍海波， 韦化. 考虑风电的电压稳定概率评估的随机响应面法[J]. 中国电机工程学报， 2012， 32（ 13）： 77-85.BAO Haibo， WEI Hua. Stochastic response surface method for probabilistic evaluation of voltage stability considering wind power[J]. Proceeding of the CSEE， 2012， 32（ 13）：77-85（ in Chinese）.

[26] HUANG S P， SANKARAN M， RAMESH R. Collocationbased stochastic finite element analysis for random field problems[J]. Probabilistic Engineering Mechanics， 2007，22（ 2）： 194-205.

[27] DEVROYE L. Non-uniform random variate generation[M].New York： Springer-Verlag， 1986.