能量和功率在分析跨区域模态中的现象时的应用

李玉想

（河海大学能源与电气学院，江苏南京 210098）

较弱连接的大型电力系统会发生持续的或欠阻尼的区域间振荡。这种动态现象通常由一些小的扰动引起，有时无法找到明显的原因。这种阻尼振荡主要在设备间的相互连接中体现出来。区域间的振荡（IAO）的本质表现为周期性的动能转换，这种转换是由本地区系统内发电机转子的相对加速度或相连地区的变化引起的。对系统振荡模型的基本特性的认识，为我们提供了关于地区间现象的稳定性的宝贵信息，同时会对辨认出参与振荡能量交换的设备以及选取控制器有一定的帮助。

通常研究IAO主要通过对系统模型的线性分析和大量的时域模拟。识别基本振荡模态的方法有许多，这些方法都基于对系统的线性模型的特征分析。文献[2]总结了一些当今在研究中可以运用的主要方法。我们也用了一些其他方法来描绘区域间现象的复杂特性，这些方法包括对电力系统信号的频谱分析和对扰动引起的振铃信号的普龙尼法识别。然而，这些方法都不能使我们了解到传输网络中能量交换的性质。

随着电力系统变得日益复杂，未来地域间振荡的形式也必然会更加复杂，很可能会通过两个或多个地域模型的结合形成复合振荡，因此需要我们对系统的动态特性进行仔细的分析。近些年来，大量替代传统方法的分析技术被建立起来，用以确定区域间振荡的基本特性。

本研究提出了一种系统分析与设计的方法，这一方法的基础是通过对动能偏差的分析达到对低频区域间振荡的分析。基于这样的构想，引入模态能量的概念来研究小扰动下临界系统动能变化的性质。这种方法与物理密切相关，很有吸引力，也可以和其他方法一同使用，例如普龙尼分析法和傅里叶变换。

1 能量与功率关系

1.1 电力系统的表示

电力系统的线性表示为：

式中，A和B是实常数矩阵；x（t）是系统在n维状态空间的轨迹；u（t）表示输入的矢量。式（1）中的状态矢量定义为：

式中，xω=[△ω1r，△ω2r，…，△ωnr，]T，是相对速度分量，xδ=[△δ1n，△δ2n，…，△δ（n-1）n，]T是相对角度分量；xz是其他系统状态向量。

在初始状态t=0时x0=x（0），方程（1）的通解是:

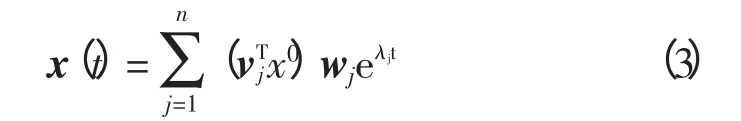
其中，λj（j=1，…，n）是系统特征值，而wj和vj是第j个系统特征值对应的左右特征向量，假设左右特征向量是标准向量，从而他们满足正交关系：

当λi≠λj；i=1，2，…，n时（wi，vj）=0；

而当λi=λj，i=j=1，2，…，n时，（wi，vj）=1。

1.2 能量关系

在式（1）描述的参考系中，n台设备的动能可以这样描述:

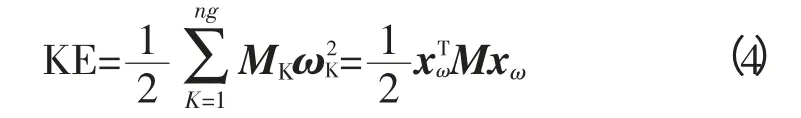
其中，M=diag|M1，…，Mng|是设备转动惯量的对角矩阵；xω是式（1）中的速度分量；ωk是第k个设备在同步参考系（SRF）中的相对速度。通过展开式（4）可以得出小扰动后系统动能的增量，一个稳定的平衡点方程为：

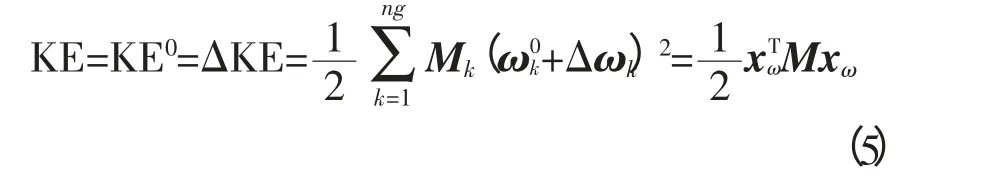
2 能量与功率系数

2.1 能量模型

由式（3）得出第k个系统设备的速度分量：

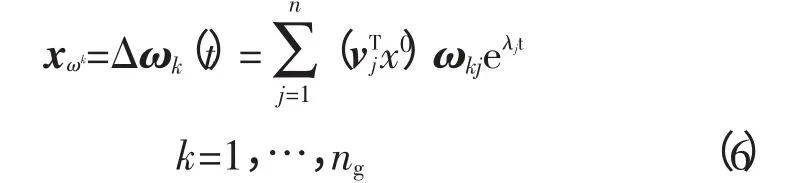
根据式（6），第k个设备的速度分量可以表示成n个线性运动模量的组合，对于一组复杂的共轭向量λk1，2=αk±jωk，这个运动是与阻尼αk、频率ωk以及相角φk相协调的。他们在这个系统中，被定义为运动模量。

因此，把式（6）带入式（5）就可以得到系统的第k个设备的动能增量：

其中

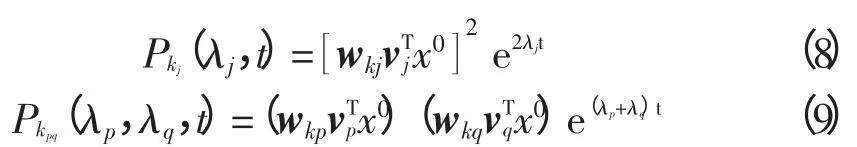
其中，Pkj是动能系数。动能系数代表了第j阶的模量在构成k阶系统能量变化的时间响应中的二阶贡献。相似的，Pkpq代表了能量模态在k阶系统动能时间响应中所起的作用，而能量模态是由p和q阶运动模态的结合。这也可以被当成一种非线性的测量方法，用以衡量模态机器法对微扰方法应用的促进。

由式（7）可以得出，一个给定系统的动能变化由2部分组成：一部分是运动模态分别起作用导致的能量变化，另一部分是每一对运动模态相结合而引起的能量变化，即λp+λq。在t=0的时刻，式（8）和式（9）中动能系数的大小，使得我们可以单列出在特定的系统中的临界设备，而动能系数的相角则体现了有能量交换的设备之间的相对振动。下文将详细地介绍我们用于识别存在能量交换的设备的程序以及设计控制器的程序。

2.2 对存在能量交换的区域的识别

针对一个模态而言，动能系数的相位可以用来将变化一致的地区或发电机划分到一个组中。假设式（8）中，第m和k台设备的j阶电磁模量的动能相角分别为φkj和φmj。那么当φkj-φmj≈±180°时，设备m和k会交换能量，而当φkj-φmj≈0°时，设备m和k会一致变化。现在将这两组设备命名为A和B，那么整个系统的动能将被表示为：

其中，KEA和KEB分别表示A和B组中动能的总和，符号∠则代表了组中设备的相角。

图1展示了区域间模态中两地区能量平衡的力学类比形式。网络中C处的阻尼控制器提供了一个摩擦力Fdamp，这代表了一个用于控制振动区域间能量交换的粘滞阻尼系数。在这项研究中，我们据此评估系统控制器对动能变化的影响。通过拓展此方法，我们希望运用能量的概念来将控制其综合起来，这正在进一步开发中。值得注意的是，可以对这种方法进行拓展，从而对复合系统振荡进行分析。

图1 区域间模态的力学类比Fig. 1 Mechanical analogy inter area mode

2.3 振型能量

通过对状态模型进行频谱分析，我们可以从一个较为有趣的角度对动能进行定义。将状态向量表示成特征向量的组合：

因此，根据麦克法兰法，总动能可以表示如下：

其中，Ej是j阶系统模态的振型能量，通过双正交性质的特征向量以及化简，我们可以证明：

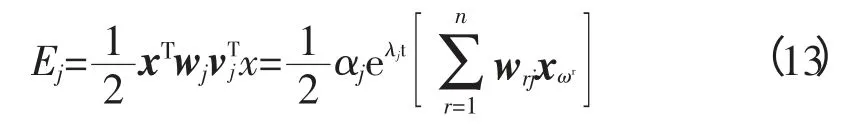
其中，αj=vTjx0。从式（12）和式（13）我们可以得出，对于一个给定的x，总动能就是各个振型能量的和。因此，将式（6）中的速度变化带入式（13）可以得出：

式（14）表达了系统发电机对于j阶振型能量的总贡献。对于任何模态j，用这个公式可以算出任意给定扰动和控制动作之后总的振型能量的变化。目前这个方法已被推广，用于求出网络中能量的分布，同时也提供了对于控制器效果的一种非线性检验方法。

3 用来确定能量交换模态的步骤

计算能量交换模态以及设计修正控制措施的步骤如下：

1）参照扰动后稳定平衡条件将式（1）线性化从而获得矩阵A同时计算系统特征值和特征向量。

2）对每一台设备，用式（8）和式（9）计算出动能系数。

3）计算与模态引起的动能变化λp和λq相对应的能量系数的大小和相位角。计算发电机组的能量系数时用2.1和2.2中的步骤结合动能系数的相角来计算。

4）按参与程度的多少降序排列设备，选出动能系数的模较大的设备，并归为同一个能量模型。

5）设计系统控制器来降低一组相同能量模型中的设备的能量交换。

4 结论

本文提出了一个用于分析低频区域间振荡的基于能量的小信号分析方法。应用基于动能变化分析的能量法，得出在振荡能量交换中最重要的设备，也可以获得对于系统振荡性质的更好的理解。此外，动能分析也使得我们对于通过运动模态的相互作用而形成的复合振荡的性质有更好的了解。另一方面，能量方法与物理有紧密的联系，可以与其他的分析方法如Prony分析和傅里叶分析结合使用。将这种方法运用到控制器的设计中，还有待于进一步的研究。

[1] 申宽育. 中国的风能资源与风力发电[J]. 西北水电，2010（1）: 76-81.SHEN Kuanyu. Wind energy resources and wind power generation in China[J]. Northwest Hydropower，2010（1）:76-81（in Chinese）.

[2] 陈达，张玮. 风能利用和研究综述[J]. 节能技术，2007（4）: 339-343.CHEN Da，ZHANG Wei. Exploitation and research on wind energy[J]. Energy Conservation Technology，2007（4）:339-343（in Chinese）.

[3] 汪如松，刘涤尘. 暂态能量函数法在区域电网中的应用研究[J]. 陕西电力，2011（9）: 6-9.WANG Rusong，LIU Dichen. Research on application of transient energy function in regional power grid[J]. Shaanxi Elcctric Power，2011（9）: 6-9（in Chinese）.

[4] 张国伟，龚光彩. 风能利用的现状及展望[J]. 节能技术，2007（1）: 71-76.ZHANG Guowei，GONG Guangcai. State of the art and prospects on wind energy[J]. Energy Conservation Technology，2007（1）: 71-76（in Chinese）.

[5] 云雷，盛超. 基于支路势能的电力系统强迫功率振荡特性分析[J]. 陕西电力，2012（11）: 12-15.YUN Lei，SHENG Chao.Reserach on forced power oscillation characteristics based on branch potential energy[J].Shaanxi Elcctric Power，2012（11）: 12-15（in Chinese）.

[6] 陈虎. 基于MATLAB的风力发电机组建模和仿真研究[J].节能技术，2012（1）: 24-28.CHEN Hu. The modeling and simulation study of wind turbine based on MATLAB[J]. Energy Conservation Technology，2012（1）: 24-28（in Chinese）.

[7] 张靠社，张增强，杨宝杰. 基于Hamilton能量函数含TCSC的电力系统非线性控制[J]. 陕西电力，2009（3）:23-26.ZHANG Kaoshe，ZHANG Zengqiang，YANG Baojie.Nonlinear control for power system with TCSC based on hamiltionian energy function[J]. Shaanxi Elcctric Power，2009（3）: 23-26（in Chinese）.

[8] 云雷，刘代刚. 基于多重扰动的跨区域电网薄弱区域的选取研究[J]. 陕西电力，2011（10）: 19-22.YUN Lei，LIU Daigang. Vulnerable region selection analysis of cross-area grid base on multi-disturbance[J].Shaanxi Elcctric Power，2011（10）: 19-22（in Chinese）.

[9] 段秦刚，赵文辉. 共振型低频振荡扰动源溯源方法综述[J]. 陕西电力，2012（1）: 42-45.DUAN Qingang，ZHAO Wenhui. A survey on disturbance source location of power system low frequency oscillation of resonance mechanism[J]. Shaanxi Elcctric Power，2012（1）: 42-45（in Chinese）.

[10] 杨春，汪灵梅，刘丽娟. 电力工业节能减排政策及现状分析[J]. 节能技术，2010（3）: 232-235.YANG Chun，WANG Lingmei，LIU Lijuan. Current status of energy-sanving and emission-reduction in electrivc power industry[J]. Energy Conservation Technology，2010（3）: 232-235（in Chinese）.

[11] 黄生琪，周菊华. 我国节能减排的意义、现状及措施[J].节能技术，2008（2）: 172-175.HUANG Shengqi，ZHOU Juhua. Studies on energy saving and pollution reduction energy conservation technology[J].Energy Conservation Technology，2008（2）: 172-175（in Chinese）.