基于扩张状态观测器的电力系统强迫扰动监测

李浪

（内江职业技术学院，四川 内江 641000）

强迫扰动是引起电力系统低频振荡的原因之一，许多专家学者对这类扰动引起的低频振荡做了大量研究[1-10]。文献[1-2]用强迫共振理论解释了该类振荡机理，指出该类振荡与负阻尼振荡的区别。文献[3]基于ARMA模态辨识的方法对2种性质的低频振荡进行了区分。文献[4-5]分别采用EMDTEO和信号能量分析法以及EEMD滤波原理和TLS-ESPRIT算法对低频振荡模式识别进行了研究。文献[6-7]分别基于等效电路分析法和能量耗散理论对电力系统强迫功率振荡的扰动源定位进行了研究。文献[8-9]对抑制电力系统低频振荡的方法进行了研究。文献[10]概述了共振型低频振荡扰动源溯源方法。引起共振型低频振荡原因也很多，包括汽轮机压力脉动[11]、水轮机尾水管压力脉动[12]、原动机功率扰动[13]、负荷持续波动[14-15]等。

以往研究概括起来主要分3个方面：1）强迫振荡机理及振荡特性研究；2）扰动源定位研究；3）引起强迫型低频振荡的原因分析与对比。而对扰动源的具体形式几乎很少。在以往的研究中一般都将扰动假想为一简谐形式，文献[11]指出实际的扰动一般都为非简谐的，往往表现得更复杂，如定常的周期脉动、非定常变化任意的持久波动及非定常突发性的冲击波动。不同的扰动形式对系统稳定性影响的差别很大。为此，需要对扰动源的具体形式进行研究。

采用观测器理论进行电力系统故障或扰动的诊断已有研究，文献[16]通过在HVDC状态方程上引入新的参数来构造一个虚拟故障，并通过迭代求解，从而实现对故障的估计。文献[17]采用ESO的方法，来实现对电机转子磁链的观测。本文在前人研究的基础上，提出采用ESO来研究电力系统强迫扰动估计问题。ESO是自抗扰控制器的核心组成部分[18]。从某种意义上，ESO是通用而实用的扰动观测器[19]，可以处理常见的系统参数未知、未建模动态、未知负载扰动等不确定性问题，不需要迭代求解。采用该观测器对单机无穷大系统原动机受到正弦波和脉冲2种形式的扰动进行仿真分析，其结果表明该方法能够准确估计出系统的扰动形式，证明了该方法的有效性。

1 扩张状态观测器基本原理

系统数学模型的一般表达式为：

式中，w为系统未知扰动；f（x，x觶，…，x（n－1））为状态变量的函数；u为控制量，x，x觶，…，x（n－1）为状态变量。

令x1（t）=x（t），x2（t）=x觶（t），…，xn（t）=x（n－1）（t），xn+1（t）=w，可得系统（1）的等价方程为：

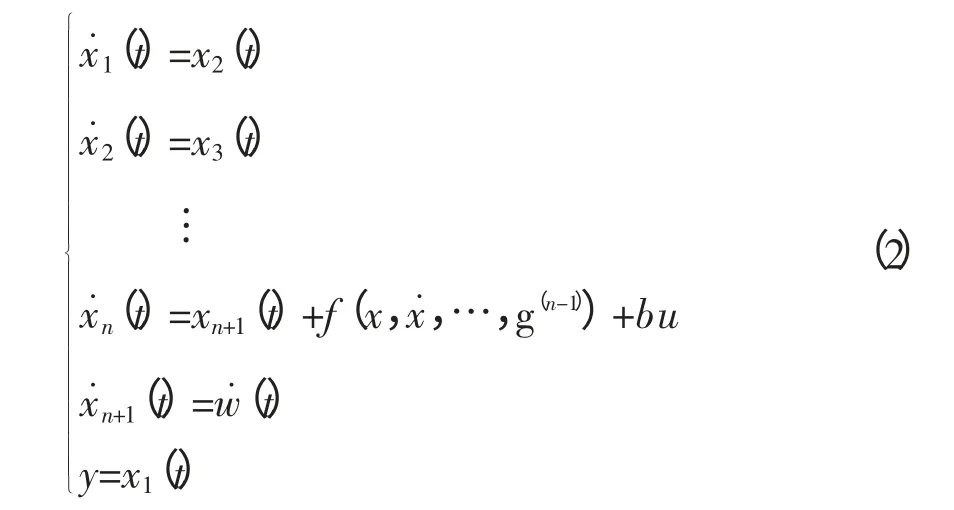
式中，xn+1（t）为系统的扩张状态，即扰动量。对系统（2）建立其扩张状态观测器为：

式中，z1，…，zn为原系统各个状态的估计值；zn+1为系统的扩张状态，即未知扰动的估计值。而fal（·）是如下形式的非光滑函数：

式中，0<α≤1，δ等于采样步长。

由式（3）可知，只要适当地选取观测器参数βi，i∈n+1，由系统的输入和输出即可实现对系统状态的估计，状态观测器框图如图1所示。

图1 状态观测器Fig. 1 State observer

2 扩张状态观测器参数整定

对于非线性扩张状态观测器的参数整定问题较为复杂，本文在文献[19]研究基础上，采用式（5）确定观测器初值并结合参数整定原则进一步对参数进行调整。式（5）为：

其中，dt为采样步长。

参数整定原则：

1）首先确定参数范围，扰动幅值越大，相应的参数β1，β2和β3也越大，尤其是β3。

2）对扰动估计滞后的大小主要取决于参数β3，β3越大滞后越小，但β3过大会导致估计值振荡。适当增大β1和β2，能有效地抑制β3过大引起的振荡。

3）同理，β1和β2过大会引起估计值发散。因此，β1，β2和β3要协调调整，在主要调整β3的同时，适当协调调整β1和β2，不断改善估计效果。

3 单机无穷大系统扩张状态观测器

3.1 系统模型

以图2所示经典模型单机无穷大系统为例，构建扩张状态观测器。

线性化的发电机运动方程为：

图2 单机无穷大系统Fig. 2 Single machine infinitive bus system

式中，F0Φ（ωt）为持续的周期性小扰动；F0为扰动幅值；ω为扰动频率；δ为发电机功角；ω0=2πf0，f0为系统基准频率；TJ为发电机惯性时间常数；D为发电机阻尼系数；KS为发电机同步转矩系数。

由式（7）可以看出，这是一个二阶常系数线性非齐次微分方程。

将式（7）改写为状态空间表达形式，令x1=x，x2=x觶，x3=hΦ（ωt），则式（7）可改写为：

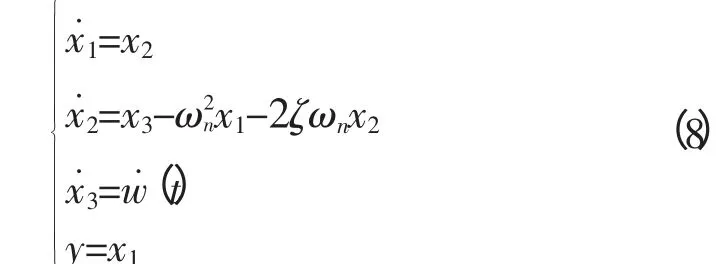
3.2 扩张状态观测器构建

仿照式（3），对式（8）建立其扩张状态观测器为：

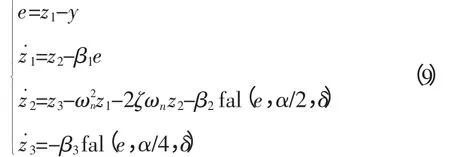
式中，z1、z2和z3分别为状态量x1、x2和x3的观测值。

由上述分析可知，扰动量为：

因此通过观测器可以实现对z3的观测，并且由式（10）最终可以得到扰动量F0Φ（ωt）。

4 仿真分析

4.1 仿真参数

图2中网络电抗是以2 220 MV·A，24 kV为基准的标幺值，忽略电阻，系统基准频率f0=50 Hz。

发电机参数（以2 220 MV·A，24 kV为基准电压）：X′d=0.3，TJ=7.0 s，D=2.0。

系统运行状态参数：P=0.9 pu，Q=0.3 pu，Et=1.0∠36° pu，EB=0.995∠0° pu。

发电机暂态电抗后电势为

系统总电抗为

同步转矩系数为

无阻尼固有振荡频率的平方为

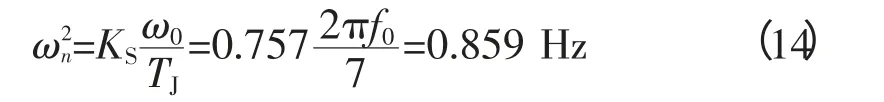
阻尼比为

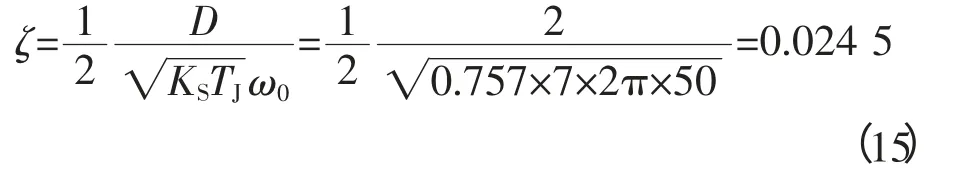
4.2 观测器仿真模型

根据式（9），在PSCAD里搭建观测器仿真模型如图3所示。

图3 观测器仿真模型Fig. 3 Observer simulation model

图3中fal模块是实现非光滑函数fal（·）的功能，采用fortran语言编写，通过PSCAD自定义模块的功能调用。

4.3 仿真结果

分别针对正弦波扰动和脉冲扰动2种形式的扰动进行了仿真，仿真结果见图4—9。图4—6为正弦波扰动下估计值与真值的比较结果；图7—9为脉冲扰动下估计值与真值的比较结果。图中实线为估计值，虚线为真值。

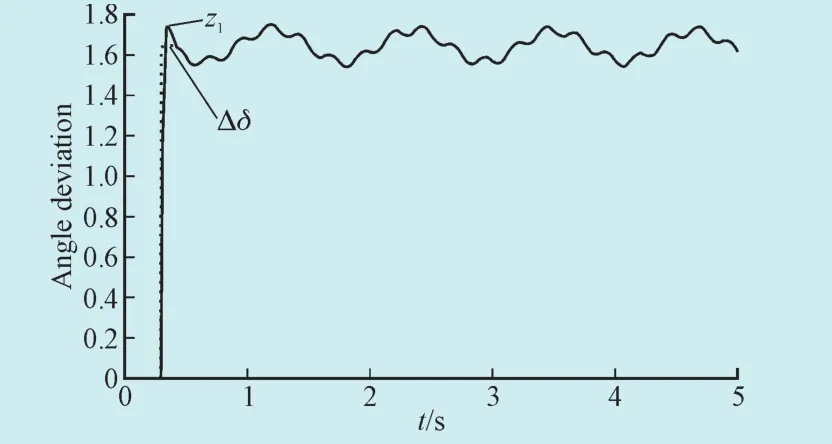
图4 Δδ估计结果对比Fig. 4 Δδ comparative estimation results

图5 Δω估计结果对比Fig. 5 Δω comparative estimation results

图6 扰动估计结果对比Fig. 6 Disturbance comparative estimation results

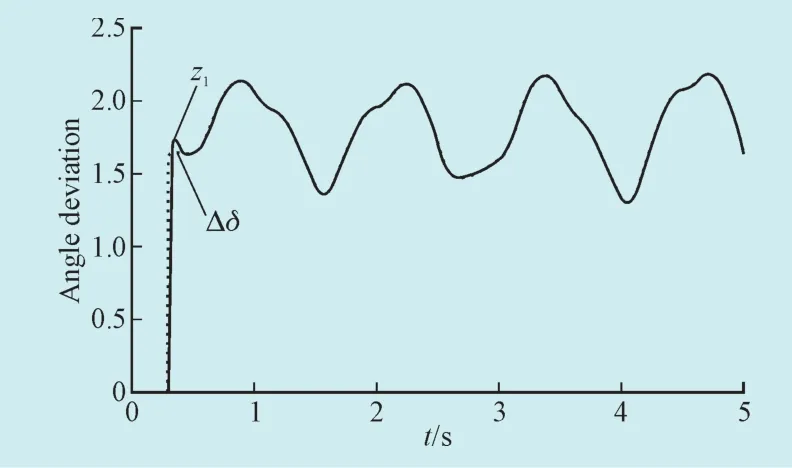
图7 Δδ估计结果对比Fig. 7 Δδ comparative estimation results

由上述对比结果可以看出，该方法可以实现对状态变量准确估计，同时对外界的强迫扰动也可实现精确的估计。

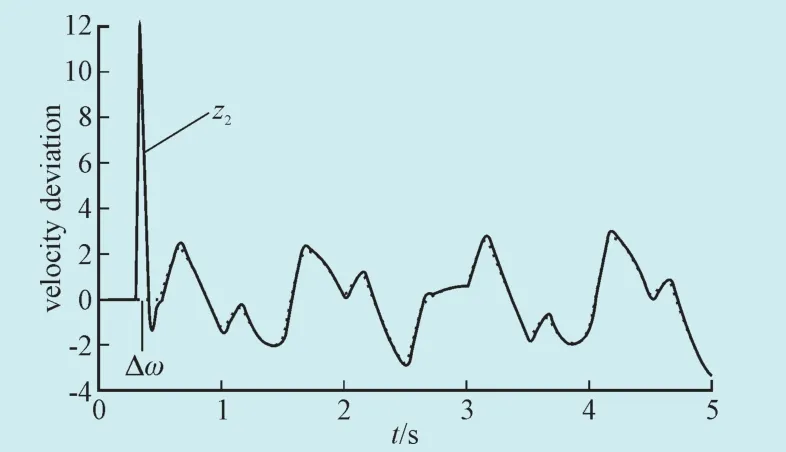
图8 Δω估计结果对比Fig. 8 Δω comparative estimation results

图9 扰动估计结果对比Fig. 9 Disturbance comparative estimation results

进一步分析了2种扰动形式对系统稳定性的影响，仿真选定扰动幅值和频率相同，仿真结果见图10和图11，虚线是脉冲扰动作用下系统功角偏差和速度偏差，实线为正弦波扰动作用下系统功角偏差和速度偏差。

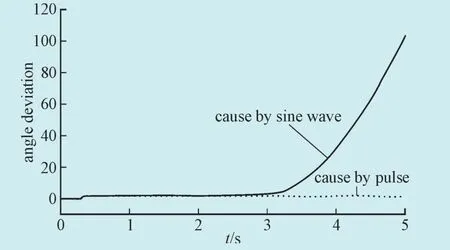
图10 两种扰动形式下功角偏差Fig. 10 Power angle deviation in the form of both disturbances

图11 两种扰动形式下速度偏差Fig. 11 Velocity deviation in the form of both disturbances

由图10和11可以看出，在扰动幅值和频率相同的情况下正弦波更容易引起系统的不稳定。

5 结论

本文采用扩张状态观测器对系统所受外界强迫扰动进行了估计，将系统所受外界强迫扰动扩张为一阶状态量，通过对单机无穷大系统原动机受到正弦波扰动和脉冲扰动2种形式的扰动仿真分析，结果表明本文所提方法能够对系统强迫扰动准确地估计，证明了该方法的有效性。并对正弦波和脉冲扰动作用下对系统稳定性的影响进行了研究，结果表明，幅值和频率相同的情况下，正弦波更容易引起系统的不稳定。

[1] 汤涌. 电力系统强迫振荡分析[J]. 电网技术，1995，19（12）：6-10.TANG Yong. The analysis of forced power oscillation in power system[J]. Power System Technology，1995，19（12）：6-10（in Chinese）.

[2] 汤涌. 电力系统强迫功率振荡的基础理论[J]. 电网技术，2006，30（10）：29-33.TANG Yong. Fundamental theory of forced power oscillation in power system[J]. Power System Technology，2006，30（10）：29-33（in Chinese）.

[3] 涂炼，董飞飞，冀星沛，等. 基于ARMA模态辨识的低频振荡性质区分[J]. 陕西电力，2013，41（5）: 9-13.TU Lian，DONG Feifei，JI Xingpei，et al. Distinction of the property of low frequency oscillation based on ARMA mode identification[J]. Shaanxi Electric Power，2013，41（5）: 9-13（in Chinese）.

[4] 王娜娜，刘涤尘，廖清芬，等. 基于EMDTEO及信号能量分析法的主导低频振荡模式识别[J]. 电工技术学报，2012，27（6）: 198-204.WANG Nana，LIU Dichen，LIAO Qingfen，et al. Identification of the dominant inertial mode based on EMDTEO and signal energy method[J]. Transactions of China Electrotechnical Society，2012，27（6）:198-204（in Chinese）.

[5] 杨小明，刘涤尘，张红丽，等. 基于改进EEMD滤波原理及TLS-ESPRIT算法的低频振荡模式识别[J]. 陕西电力，2012，40（7）: 23-27.YANG Xiaoming，LIU Dichen，ZHANG Hongli，et al.Identification of low frequency osillation modes based on improved EEMD filtering technique and TLS-ESPRIT algorithm[J]. Shaanxi Electric Power，2012，40（7）: 23-27（in Chinese）.

[6] 杨毅强，刘天琪，李兴源，等. 电力系统强迫功率振荡的等效电路定位分析法[J]. 电网技术，2012，36（11）:101-108.YANG Yiqiang，LIU Tianqi，LI Xingyuan，et al. An equivalent circuit approach to locate source of power system forced power oscillation[J]. Power System Technology，2012，36（11）: 101-108（in Chinese）.

[7] 胡伟，林涛，高玉喜，等. 基于耗散功率的区域电网强迫功率振荡扰动源定位[J]. 高电压技术，2012，38（4）:1006-1011.HU Wei，LIN Tao，GAO Yuxi，et al. Disturbance source location of forced power oscillation in regional power grid based on dissipation power[J]. High Voltage Engineering，2012，38（4）: 1006-1011（in Chinese）.

[8] 贾体康，向铁元. 利用SSSC装置抑制电力系统低频振荡的研究[J]. 陕西电力，2014，42（8）: 72-75.JIA Tikang，XIANG Tieyuan. Study on damping of lowfrequency oscillations in power system by using SSSC device[J]. Shaanxi Electric Power，2014，42（8）: 72-75（in Chinese）.

[9] 谢亦丰，祝明华，熊连松，等. 储能装置与PSS配合控制对电力系统低频振荡的抑制效果研究[J]. 陕西电力，2013，41（9）: 5-9.XIE Yifeng，ZHU Minghua，XIONG Liansong，et al.Research on coordinated effect of energy storage device and PSS on suppressing low-frequeccy oscillation in power system[J]. Shaanxi Electric Power，2013，41（9）: 5-9（in Chinese）.

[10] 段秦刚，赵文辉，马进，等. 共振型低频振荡扰动源溯源方法综述[J]. 陕西电力，2012，40（1）: 42-45.DUN Qingang，ZHAO Wenhui，MA Jin，et al. A survey on disturbance source location of power system low frequency oscillation of resonance mechanism[J]. Shaanxi Electric Power，2012，40（1）: 42-45（in Chinese）.

[11] 韩志勇，贺仁睦，徐衍会. 汽轮机压力脉动引发电力系统低频振荡的共振机理分析[J]. 中国电机工程学报，2008，28（1）：47-51.HAN Zhiyong，HE Renmu，XU Yanhui.Study on resonance mechanism of power system low frequency oscillation induced by turbopressure pulsation[J]. Proceedings of the CSEE，2008，28（1）：47-51（in Chinese）.

[12] 汤凡，刘天琪，李兴源. 大型水电机组与交直流互联电网的耦合作用[J]. 电网技术，2011，35（3）：38-43.TANG Fan，LIU Tianqi，LI Xingyuan.Analysis on coupling of large hydraulic turbine with ACDC interconnected power system[J]. Power System Technology，2011，35（3）：38-43（in Chinese）.

[13] 董超，云雷，刘涤尘，等. 原动机周期性扰动引发强迫功率振荡特性研究[J]. 电网与清洁能源，2012，28（4）:35-41.DONG Chao，YUN Lei，LIU Dichen，et al.Researchon the properties of forced oscillations caused by turbine’s periodic disturbance[J]. Power System and Clean Energy，2012，28（4）: 35-41（in Chinese）.

[14] YU Yiping，MIN Yong，CHEN Lei，et al. The disturbance source identification of forced power oscillation caused by continuous cyclical load[C]// 2011 4th international conference on electric utility deregulation and restructuring and power technologies（DRPT）. Weihai，China：IEEE，2011：308-313.

[15] 余一平，闵勇，陈磊，等. 周期性负荷扰动引发强迫功率振荡分析[J]. 电力系统自动化，2010，34（6）：7-11.YU Yiping，MIN Yong，CHEN Lei，et al. Analysis of forced power oscillation caused by continuous load disturbances[J]. Automation of Electric Power Systems，2010，34（6）：7-11（in Chinese）.

[16] 颜秉勇，田作华，施颂椒，等. 高压直流输电系统故障诊断新方法[J]. 电力系统自动化，2007，31（16）: 57-61.YAN Bingyong，TIAN Zuohua，SHI Songjiao，et al. A new method for fault diagnosis in HVDC systems[J]. Automation of Electric Power Systems，2007，31（16）: 57-61（in Chinese）.

[17] 林飞，张春朋，宋文超，等. 基于扩张状态观测器的感应电机转子磁链观测[J]. 中国电机工程学报，2003，23（4）: 145-147.LIN Fei，ZHANG Chunpeng，SONG Wenchao，et al. Flux observer of induction motor based on extended state observer[J]. Proceedings of the CSEE，2003，23（4）: 145-147（in Chinese）.

[18] 韩京清. 一类不确定对象的扩张状态观测器[J]. 控制与决策，1995，10（1）：85-88.HAN Jingqing. The extended state observer of a class of uncertain system[J]. Control and Decision，1995，10（1）：85-88（in Chinese）.

[19] 韩京清. 自抗扰控制技术[M]. 北京：国防工业出版社，2013：183-242.