基于总体平均经验模态分解与改进Elm an神经网络的风功率组合预测

杨楠，周峥，李臻，崔家展，郑翔宇，杨俊

（1. 湖北省微电网工程技术研究中心（三峡大学），湖北 宜昌 443002；2. 甘肃省电力科学研究院，甘肃 兰州 730050）

在能源问题日益突出的今天，风能作为一种分布广的可再生能源受到人们的广泛关注。随着风力发电技术的日渐成熟，风电占电力系统发电总量的比例也逐渐增加。然而，风能的随机性和间歇性等特点对电能质量和电网的安全、稳定运行造成了不良影响，而对风电功率进行有效的预测是降低上述影响和系统的运行成本，提高风电穿透功率极限的有效手段[1]，因此，研究风电风功率的短期预测方法具有重要的理论和实际意义。

风功率的短期预测一般包括物理方法和统计方法两种。物理方法[2]主要考虑天气数据以及风电机组的技术参数，寻求风电机组轮毅高度处的风速最优估计值，最后根据风电场的有功出力函数计算得到其输出功率，由于该方法过分依赖完善的数值天气预报信息，且预测精度受风电有功出力模型建模精度影响较大，因此工程实用性较低。统计方法不考虑风速变化的物理过程，而是根据大量实测数据直接对风电场输出功率进行预测，因而具有较高的实用性。目前常用的统计学预测方法有持续法、时间序列法、人工神经网络法、支持向量机法等[3-6]。持续法方法虽然简单但预测误差较大。时间序列法存在模型选取困难的缺陷，若选取低阶模型则预测精度达不到要求，若选取高阶模型则会导致参数估计难度过大。支持向量机虽然实现了结构风险最小化，但其核函数参数和惩罚因子较难选择。Elman神经网络[7]是一种在时间序列预测中运用较为广泛的反馈型神经网络，与前馈式神经网络相比，它还有一个承接层，通过联接记忆将上一个时刻的隐层状态连同当前时刻的网络输入一起作为隐含层的输入，相当于状态反馈，从而有效增强了其处理动态信息和非线性拟合的能力，考虑到风功率本身的非线性和随机性，Elman神经网络将成为风功率短期预测的有效思路之一。

但是要将Elman神经网络应用于风功率短期预测，依然存在两方面问题：一方面，Elman神经网络结构较难确定，限制了其在风功率短期预测问题中的适用性；另一方面，风功率本身具有的非平稳性会降低神经网络方法的预测精度。虽然有文献尝试利用小波分析[8]和经验模态分解（EMD）[9]先将非平稳风功率序列转化为一系列相对简单、具有一定规律性的子序列，然后再进行预测，以提高预测精度，但由于小波分析的小波基和分解尺度较难选择，而EMD分解则会出现模态混叠的现象，上述方法的预测效果尚存在一定的提升空间。

综上所述，本文提出了一种基于Elman神经网络的风功率组合预测方法。一方面，针对Elman神经网络结构确定困难的问题，本文提出了一种基于相空间重构的Elman神经网络改进策略，将风功率序列进行相空间重构并作为网络的输入，在此基础上以训练误差最小获取最优隐含层节点数。另一方面，针对风功率本身的非平稳性，本文利用一种改进的EMD方法即总体平均经验模态分解（EEMD）[10]，对风功率进行预处理，有效避免了传统EMD方法中的混叠现象，且其基函数不需要事先确定，而是在分解过程中由信号本身的特性确定，避免了小波分析方法中小波基确定困难的问题。基于实际数据的仿真结果表明，本文提出的基于EEMD-改进Elman神经网络的短期风功率组合预测模型，有效解决了风功率非平稳性对神经网络方法预测精度的干扰问题，相比于其他传统风功率预测方法具有更高的预测精度。

1 基于EEMD方法的风功率预处理

作为一种广泛用于非平稳信号预处理的方法，EMD能将复杂的时间序列平稳化，得到几个本征模函数（intrinic model function，IMF）分量，并且每个分量之间相互独立，但是，当出现信号的时间尺度存在跳跃性变化时，仅仅做一次EMD分解无法根据特征时间尺度有效分离出不同的模态成分，即在分解过程中会出现模态混叠现象。因此，为提高风功率预测方法的适用性，本文提出了一种改进的EMD方法，即EEMD方法对风功率进行预处理，该方法将白噪声序列添加到原始序列中，然后对其进行多次EMD分解，将分解得到的多组IMF的均值作为其真实分量，从而避免了混沌重叠现象[11-12]。其具体步骤如下：

Step1：初始化过程。初始化EMD执行次数M次，每次添加噪声的幅值为k。

Step2：向风功率时间序列x（t）添加正态分布白噪声n（t），执行第m次EMD过程：

1）找出序列x（t）的所有极小值与极大值，利用三次样条函数差值拟合其上下包络线。

2）计算上下包络线的平均值n（t），h（t）=x（t）－m（t）。

3）判断h（t）是否满足IMF的定义，满足则将h（t）作为第一个IMF，否则将h（t）作为原始序列重复1）和2）直至满足IMF的定义。

4）将IMF分量从原始信号中分离，r（t）=x（t）－h（t），将r（t）作为新的序列重复上述步骤，得到剩余的IMF分量和余量，余量为单调函数。

Step3：总体平均运算。对M次EMD分解得到的每个IMF计算均值作为最终结果。

执行M次EMD分解中添加的白噪声序列满足正态分布且相互独立，根据文献[13]可知，当M=100，添加噪声的幅值k=0.1时，所取得的效果较好。

2 基于改进Elman神经网络预测模型

2.1 Elman神经网络

Elman神经网络[14]是一种反馈式的神经网络（图1），其主要分为4层：输入层、隐含层、承接层（关联层）和输出层，其网络结构如图所示。输入层的单元仅起信号输入作用，隐含层单元的传递函数常采用S函数，输出层单元起线性加权作用。承接层多被用于层内或层间的反馈联结，使得其能够表达输入与输出之间在时间上的延迟，可以认为是一个一步延时算子。

图1 Elman神经网络结构Fig. 1 The structure of the Elman neural network

Elman神经网络的非线性状态空间表达式为：

式中：k为时刻；y，x，u，xc分别为1维输出节点向量，m维隐含层节点单元向量，n维输入向量和m维反馈状态向量；w3，w2，w1分别为隐含层到输出层、输入层到隐含层、承接层到隐含层的连接权值矩阵；f（·）为隐含层神经元的传递函数；b1和b2分别为输入层和隐含层的阈值。

2.2 基于相空间重构的Elman神经网络改进策略

对于风功率的时间序列预测，下一时刻功率预测值通常采用前m时刻的实测值作为输入，输入层的节点数m常用试验法和经验公式来确定。为避免输入节点数选取的任意性和丢失信息的问题，本文采用相空间重构的方法，利用将非线性的风功率时间序列重构后，得出的相空间来反映该序列的内部规律[15]。

其具体操作为，对风功率时间序列{p（t）}，t=1，2，3，…，N，选择一个适当的嵌入维数m和延迟时间t，可得到满足式（4）的新的状态空间，即重构的风功率时间序列相空间：

其中：t=1，2，3，…，M，M=N－（m－1）τ。

求取相空间重构的延迟时间τ和嵌入维数m已有很多成熟的算法，本文运用C-C方法[16]。选取相空间重构中的饱和嵌入维数m作为神经网络的输入节点数。

Elman神经网络的隐含层节点数对Elman神经网络预测精度有较大的影响，若隐含层节点数过少，不能很好地学习；节点数过多，训练时间增加，网络容易过拟合。Kolmogorov定理[17]证明了在合理的结构和适当的权值条件下3层前向网络可以满意再现任意连续函数，若网络的输入层节点数有m个，则隐含层节点数约为2m+1个单元。在确定隐含层节点数的理论值之后，运用训练误差最小的方法来选取最优节点数。其具体步骤如下：

1）利用相空间重构法将风功率序列重构，获取输入数据及其输入节点数m。

2）将待优化隐层节点个数的取值范围定为n∈［2m－4，2m+6］。

3）循环选取隐含层节点数对Elman神经网络进行训练，选取训练误差最小的节点为最优节点。

3 基于EEMD-改进Elman神经网络的短期风功率预测方法

本文提出的基于EEMD-改进Elman神经网络的短期风功率预测方法的总体思路为：首先利用EEMD将风功率序列按不同频率逐级分解，得到不同的IMF分量以减少其非平稳特性；然后对各分量进行相空间重构，分别建立改进的Elman神经网络预测模型，从而减小分量之间的相互干扰；最后叠加各分量的预测结果得到最终预测数据。其预测流程图如图2所示。

图2 EEMD-改进Elman神经网络预测流程图Fig. 2 Prediction flow chart of the EEMD-improved Elman neural network

4 算例分析

4.1 数据的选取及预处理

本文选取湖北某风电场一号机组的实测风功率数据作为算例进行风功率预测，该数据的采样周期为10 min，机组的额定功率为850 kW。为研究方便，选取停机时间点尽可能少数据段进行仿真分析，选取360个连续功率数据点，前300个用于训练，后60个用于测试和分析。其功率曲线如图3所示。

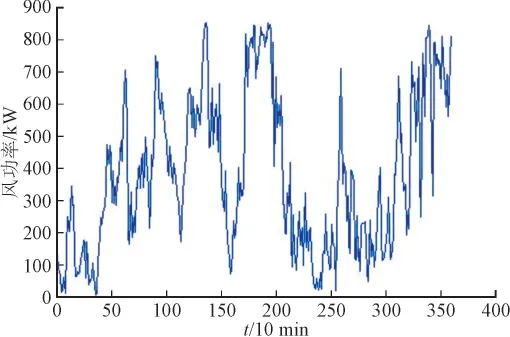
图3 风功率曲线图Fig. 3 Wind power curve

利用EEMD方法对原始风功率时间序列进行分解，产生了7个IMF分量和1个余量，结果如图4所示。

由图3中各子序列的特性可以看出，分量IMF1-IMF2频率较高，其周期性不明显，波动仍很剧烈。分量IMF3-IMF7频率较低，且其周期性较为明显。余量r（t）为一条幅值较高，单调递增的曲线。

为验证本文EEMD分解方法的有效性，采用EMD方法对风功率进行分解，其结果如图4所示。

由图5可知，在分量IMF2-IMF4中出现了不同频率的混叠现象，而图3各分量频率都较为平稳。可见，相比于传统EMD分解方法，本文提出的EEMD分解可以有效避免风功率分解过程中的模态混叠现象。

风电功率数据经EEMD分解后，各分量数据较大，还需对它们归一化处理后再进行预测。其归一化处理及还原如式（5）和式（6）：

式中：yi为样本中的某个数据归一化后的结果；xmax和xmin分别为样本中该组变量数据的最大值和最小值。

4.2 预测结果分析

图4 风功率经EEMD分解后各分量图Fig. 4 Diagram of each wind power component through EEMD decomposing

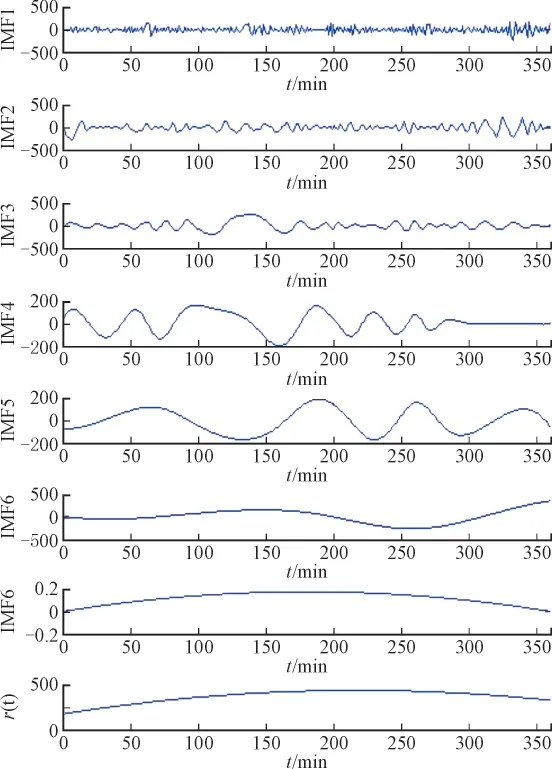
图5 风功率经EMD分解后各分量图Fig. 5 Diagram of each wind power component through EMD decomposing

为了对预测结果的精度和可靠性进行定量评估，本文采用以下几种指标作为预测精度分析指标[18]：

1）均方误差

2）平均绝对百分比误差

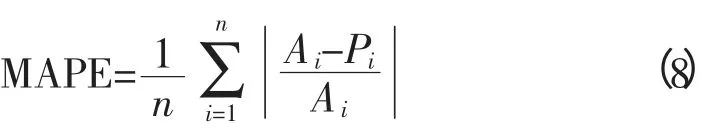
3）均方百分比误差

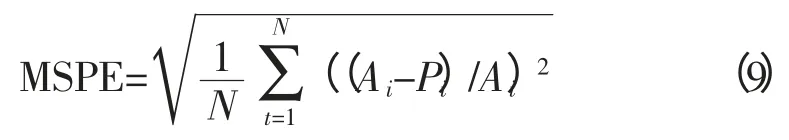
式中：Ai为第i个预测点的实测值；pi为第i个预测点的预测值；N为预测点的个数。

对各个IMF分量分别建立Elman神经网络预测模型进行一步预测，各IMF分量的预测模型参数及其误差如表1所示。

表1 各IMF预测模型参数及误差Tab. 1 The IMF prediction model parameters and errors

最后再将各个模型的预测结果叠加得到最终风功率预测值，图6给出了EEMD-Elman神经网络模型预测结果对比图。

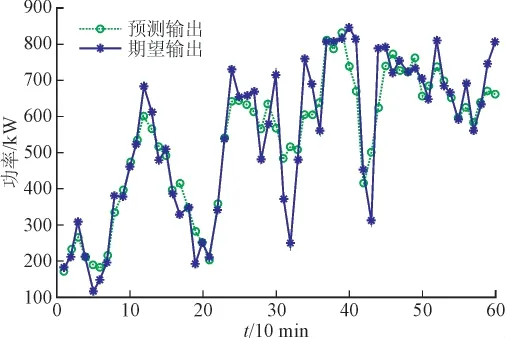
图6 EEMD-改进Elman神经网络预测结果Fig. 6 The predicting results of the EEMD-improved Elman neural network

由图6可知，本文的预测值能紧跟实际值的变化趋势，具有较高的拟合精度，从而验证了本文所提预测模型的有效性。

为进一步的对比研究，本文还利用单一的BP、Elman神经网络预测模型和EMD-Elman预测模型进行风功率预测，其预测误差指标对比如表2所示。

表2 模型性能指标Tab. 2 Model performance index

由表2可知，与其他各个预测模型的性能指标相比，本文所提模型精度更高，具有一定的先进性。其原因是，EEMD将非平稳特性的风功率序列转化为一系列的子序列，再对具有一定规律的子序列进行预测，降低了预测难度，因此相对于单一的预测方法本文组合预测模型预测精度较高；而EEMD利用噪声特性避免了EMD的混叠现象，利用EEMD进行分解，预测效果也会更好。

5 结论

本文提出了一种基于EEMD-改进Elman神经网络的风功率预测方法，其主要结论如下：

1）利用EEMD分解将复杂的风功率序列分解为一系列相对简单的子分量，不仅可有效降低风功率的非平稳性，为后续风功率预测奠定基础，还可以避免传统EMD分解过程中的模态混叠现象，提高后续风功率预测的精度。

2）Elman神经网络具有较强的非线性拟合能力，并根据相空间重构和训练误差最小的方法获取模型结构的参数，可进一步提高预测精度。

3）从本文模型的预测结果及与其他模型的对比分析可以看出，本文的预测建模思路具有一定的先进性，取得了较好的预测效果。

[1] 王健，严干贵，宋薇，等. 风电功率预测技术综述[J]. 东北电力大学学报，2011，31（3）: 20-24.WANG Jian，YAN Gangui，SONG Wei，et al. Summarization of wind power prediction technology[J]. Joumal of Northeast Dianli University，2011，31（3）: 20-24 （in Chinese）.

[2] 谷兴凯，范高锋，王晓蓉，等.风电功率预测技术综述[J].电网技术，2007，31（2）: 335-338.GU Xingkai，FAN Gaofeng，WANG Xiaorong，et al. Summarization of wind power prediction technology[J].Power System Technology，2007，31（2）: 335-338（in Chinese）.

[3] 冬雷，王丽婕，高爽. 基于混沌时间序列的大型风电场发电功率预测建模与研·究[J]. 电工技术学报，2008，23（12）: 125-129.DONG Lei，WANG Lijie，GAO Shuang. Modeling and analysis of prediction of wind power generation in the large wind farm based on chaotic time series[J]. Transactions of China Electrotechnical Society，2008，23（12）: 125-129（in Chinese）.

[4] PEIYUAN C，PEDERSEN T，BAK J B，et al. ARIMAbased time series model of stochastic wind power generation[J]. IEEE Transactions on Power Systems，2010，25（2）: 667-676.

[5] 王贺，胡志坚，张翌辉，等. 基于IPSO-LSSVM的风电功率短期预测研究[J]. 电力系统保护与控制，2012，40（24）：107-112.WANG He，HU Zhijian，ZHANG Yihui，et al. Shortterm prediction wind power based on IPSO-LSSVM[J].Power System Prediction and Control，2012，40（24）：107-112（in Chinese）.

[6] 张青贵，人工神经网络导论[M]. 北京：中国水利水电出版社，2004.

[7] 朱晟，蒋传文，侯志俭. 基于气象负荷因子的Elman祌经网络短期负荷预测[J]. 电力系统及其自动化学报，2005，17（01）: 23-26.ZHU Cheng，JIANG Chuanwen，HOU Zhijian. Application of a weather component based on Elman neural network to short-term load forcasting[J]. Proceedings of the CSUEPSA，2005，17（01）: 23-26（in Chinese）.

[8] 李洪涛，吴晓文. 基于小波变换和数学形态学的局部放电信号降噪算法的研究[J]. 陕西电力，2013，12（6）: 1-5.LI Hongtao，WU Xiaowen. Study on denoising of partial discharge signals based on wavelet transform and mathematical morphology[J]. Shaanxi Electric Power，2013，12（6）: 1-5（in Chinese）.

[9] HUANG N E，SHEN Z，LONG S R. The empirical mode decomposition and the Hilbert spectrum for nonlinear andnon-stationary time series analysis[J]. Proceedings of the Royal Society Soc Lond，1998，454（1971）: 903-995.

[10] 刘岱，庞松岭，骆伟. 基于EEMD与动态神经网络的短期负荷预测[J]. 东北电力大学学报，2009，29（6）: 20-26.LIU Dai，PANG Songling，LUO Wei. Short term load EEMD and dynamic prediction based on artificial neural network[J]. Joumal of Northeast Dianli University，2009，29（6）: 20-26（in Chinese）.

[11] 叶林，刘鹏. 基于经验模态分解和支持向量机的短期风电功率组合预测模型[J]. 中国电机工程学报，2011，31（31）: 102-107.YE Lin，LIU Peng. Combined model based on EMD-SVM for short-term wind power prediction[J]. Proceedings of the CESS，2011，31（31）: 102-107（in Chinese）.

[12] 常鹏，高亚静，张琳，等. 基于EEMD与时间序列法的短期风电场功率预测[J]. 电力科学与工程，2012，28（3）:33-39.CHANG Peng，GAO Yajing，ZHANG Lin，et al. EEMD and short-term wind power forecasting based on time sequence method[J]. Electric Power Science and Engineering，2012，28（3）: 33-39（in Chinese）.

[13] WU Z，HUANG N E. Ensemble empirical mode decomposition:a noise-assisted data analysis method[J]. Advances in Adaptive Data Analysis，2009，1（1）: 1-41.

[14] 张靠社，杨剑. 基于Elman神经网络的短期风电功率预测[J]. 电网与清洁能源，2012，28（12）: 87-91.ZHANG Kaoshe，YANG Jian. Short-term wind power forecasting based on Elman neural network[J]. Power System and Clean Energy，2012，28（12）: 87-91（in Chinese）.

[15] 韩敏. 混沌时间序列预测理论与方法[M]. 北京：中国水利水电出版社，2007：24-155.

[16] KIM H S，EYKHOLT R，SALAS J D. Nonlinear dynamics，delay times and embedding windows[J]. Physica：D，1999，127: 48-60.

[17] 梁海峰，涂光瑜，唐红卫. 遗传神经网络在电力系统短期负荷预测中的应用[J]. 电网技术，2001，25（1）: 49-53.LIANG Haifeng，TU Guangyu，TANG Hongwei. Application of genetic algorithm neural network for short term load forecasting of power system[J]. Power System Technology，2001，25（1）: 49-53（in Chinese）.

[18] 陈华友，刘春林. 基于IOWA算子的组合预测方法[J]. 预测，2003（6）：61-65.CHEN Huayou，LIU Chunlin. A kind of combination forecasting method baesd on Induced Ordered Weighted Averaging （IOWA）operators[J]. Forecasting，2003（6）:61-65（in Chinese）.