风水互补微电网的功率波动节能控制数学建模
刘志红,刘明明
(1. 郑州财经学院 计算机系,河南 郑州 450044;2. 郑州财经学院 机电工程系,河南 郑州 450044)
在国内,随着科技技术水平的不断提升,风水互补微电网以其节能环保的优势在各行业的建设中都占据着十分重要的位置[1-3]。然而在应用的过程中,如何能够有效地克服风能、水能存在的波动性特征,更好地发挥其能源效益成为了该领域亟待解决的主要问题[4-6]。而风水互补微电网的功率波动节能控制数学建模方法则是解决这一问题的有效途径,引起了很多专家与学者的关注。由于风水互补微电网的功率波动节能控制数学建模方法具有深远的发展意义,因此也成为了业内人士研究的焦点课题,受到了广泛的关注,同时也出现了很多好的方法[7]。
文献[8]提出了分别从风水互补微电网的运行成本角度和效益角度对风水互补微电网运行系统进行分析,建立了风水互补微电网的功率波动节能控制数学模型。该方法较为简单,但是存在建模误差大的问题。文献[9]提出了基于神经网络模糊算法的风水互补微电网的功率波动节能控制方法。该方法依据单神经元PID控制和神经网络模糊控制对风水互补微电网的动力系统进行了功率匹配,进而建立了风水互补微电网的功率波动节能控制数学模型。该方法鲁棒性强,但是采用当前的算法进行建模时受到大量的外界因素干扰,存在功率波动节能控制效果不佳的问题。文献[10]重点研究了依据风水互补微电网系统的恒功率和变功率协调控制理论,建立了风水互补微电网的功率波动节能控制数学模型。该方法较为精确,但是存在计算过于繁琐,耗时长的问题。
针对上述问题的产生,提出了一种基于功率曲线算法的风水互补微电网的功率波动节能控制数学建模方法。该方法针对运行的风水互补微电网系统进行分析,先计算出系统在不同自然条件下所需要的发电最大功率,依据系统在不同条件下对功率的需求设置2条或多条发电机机外特性曲线,在此基础上将风水互补微电网的功率波动节能控制问题转换为发电机与其功率平衡控制的问题,在保证负荷需求的基础上,以最大化利用风能和水能为原则,以整个系统的运行发电成本最低为目标建立风水互补微电网的功率波动节能控制数学模型。实验仿真证明,基于功率曲线算法的风水互补微电网的功率波动节能控制数学建模方法建模精确度高,鲁棒性强。
1 微电网的功率波动节能控制建模原理
由风水互补所构建的独立运行的直流母线型微网系统称为风水互补微电网系统,而在风水互补微电网的功率波动节能控制建模过程中,风力发电机将风能转换为与风速成一定关系的三相交流电,微水能经水力发电机输出交流电,二者产生的电量通过相应的DC/DC变换器进行最大功率跟踪,同时经控制器接入直流母线上,当控制器接上电后处于待机状态,收到开机指令后,依据读取的各单元状态数据,决定下一个状态,实现对风力发电机和水力发电输出的电量灵活控制,风力发电机和水力发电机输出的电量一般经直流母线会配备给直流负荷供电,但是若系统中出现交流负荷时,需经逆变器给交流负荷供电。具体的步骤如下详述:
在风水互补微电网的功率波动节能控制建模过程中,不考虑风水互补机械传动效率时,可以得出下式:

式中:p1为风力发电机输出功率;n1为风力发电机的转速;M1为水力发电机的转速;q为水力发电机的输出功率。
综上所述可以说明风水互补微电网的功率波动节能控制建模原理,建立了风水互补微电网的功率波动节能控制模型。
2 微电网节能控制建模优化方法相关原理
针对采用当前的算法进行建模时受到大量的外界因素干扰,存在功率波动节能控制效果不佳的问题,提出了一种基于功率曲线算法的风水互补微电网的功率波动节能控制数学建模方法。
2.1 发电机的最大功率计算
在风水互补微电网的功率波动节能控制优化建模过程中,针对运行的风水互补微电网系统进行分析,先计算出系统在不同自然条件状态下所需要的发电最大功率,依据系统在不同条件下对功率的需求设置2条或多条发电机机外特性曲线。具体的步骤如下详述。
在风水互补微电网的功率波动节能控制建模过程中,假设Me为风力发电机与水力发电机功率较大和较小的2条曲线上某一负载扭矩,Ne1和Ne2分别为对应发电的功率,ge1和ge2分别代表风力发电机与水力发电机最大功率耗值,ne1和ne2分别为不同发电机的转速,则利用下式可以计算出由Ge为的风力发电机与水力发电机小时功耗的理论值:

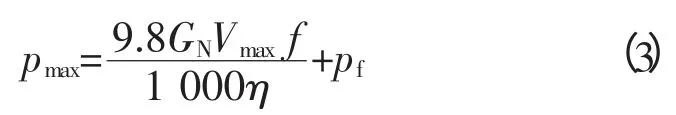
在上式中,需要满足ne1≥ne2ge1≥ge2的条件,则在相同的工况下,依据下式可以计算出系统在不同自然条件下所需要的发电最大功率pmax:式中:Vmax为不同自然条件下风力发电机与水力发电机最大作业速度;GN为发电机发电的总质量;η为发电系统电机动力传动总效率;pf为发电机的辅助功率。pf通常会取发电机功率的15%,而f值取0.75,可以将上式重新整理,利用下式表述:

在风水互补微电网的功率波动节能控制建模过程中,依据上述结论,设置3条发电机机外特性曲线,表述为1,2,3,分别对应的额定功率为115 kW,130 kW,148 kW,其中,15 kW功率曲线用于控制资源欠佳时处于失电状态下发电机的功率,130 kW功率曲线用于控制资源欠佳时状态下发电机的功率,148 kW功率曲线为发电机的原始控制曲线。
综上所述可以说明,在风水互补微电网的功率波动节能控制建模过程中,针对运行的风水互补微电网系统进行分析,先计算出系统在不同自然条件下所需要的发电最大功率,依据系统在不同条件下对功率的需求设置2条或多条发电机机外特性曲线,为实现风水互补微电网的功率波动节能控制优化建模奠定了基础。
2.2 微电网的功率波动节能控制建模的实现
在风水互补微电网的功率波动节能控制优化建模过程中,将风水互补微电网的功率波动节能控制问题转换为发电机与其功率平衡控制的问题,在保证负荷需求的基础上,以最大化利用风能和水能为原则,以整个系统的运行发电成本最低为目标建立风水互补微电网的功率波动节能控制数学模型。具体的步骤如下详述。
在风水互补微电网的功率波动节能控制建模过程中,各单元在正常的情况下,工作处于闭环调节状态,控制各项参数在限值以内,当出现不同的自然条件时,运行参数越限时,才会产生保护动作。因为依据不同自然条件状态的变化,预测风力发电机组、水力发电机组的出力情况以及负荷情况,在满足负荷用电的条件下,将风水互补微电网的功率波动节能控制问题转换为发电机与其功率平衡控制的问题。具体的步骤如下详述。
1)风力与水力发电机的功率平衡约束控制。
在风水互补微电网的功率波动节能控制优化建模过程中,将风力与水力发电机的功率控制在大于等于负荷所需功率p1(t)上:

2)风力与水力发电机的出力。
在风水互补微电网的功率波动节能控制优化建模过程中,无论是风力发电机组还是水力发电机组都必须满足其最大的出力限量,利用下式表示:

式中:由pimin、pimax为各个发电机组的最小、最大出力功率。
3)在风水互补微电网的功率波动节能控制优化建模过程中,蓄电池的运行状态必须满足以下2个控制条件:
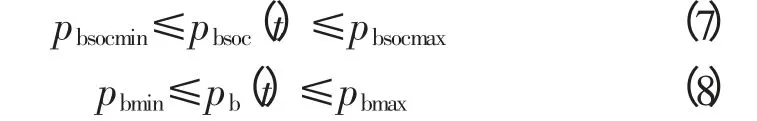
式中:pbsocmin和pbsocmax分别为蓄电池最小、最大的荷电量;pbmin和pbmax分别为蓄电池最小和最大充放电功率。
在风水互补微电网的功率波动节能控制优化建模过程中,在通常情况下风力、水力发电的单位成本取决于投资成本、燃料成本、维护成本、产率等多种因素,因此利用下式可以计算其目标函数:
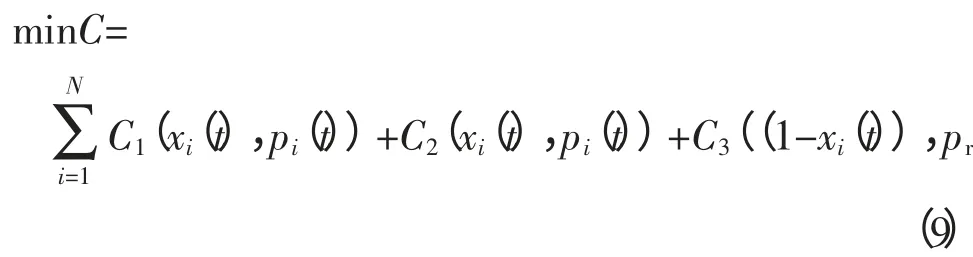
在风水互补微电网的功率波动节能控制优化建模过程中,利用下式建立水力发电机的输出功率节能控制的数学模型:

在风水互补微电网的功率波动节能控制优化建模过程中,利用下式建立发电机的输出功率节能控制的数学模型:

式中:v(t)为t时段的实时风速;vc为切入风速;vr为额定风速;pr为对应不同风力发电机型号的额定功率。
在风水互补微电网的功率波动节能控制优化建模过程中,蓄电池是风水互补微电网系统的储能装置中不可获缺的部分,它可以有效地平衡发电机的输出功率,也可以作为备用电源稳定风水互补微电网的运行,利用下式计算蓄电池的荷电状态:

式中:ηinv为逆变器的效率;ηb为蓄电池的充电效率;p1(t)为t时段负荷所需的功率。
综上所述可以证明风水互补微电网的功率波动节能控制数学建模优化原理,建立了风水互补微电网的功率波动节能控制数学模型。
3 仿真实验证明
为了证明基于功率曲线算法的风水互补微电网的功率波动节能控制数学建模方法的有效性,需要进行一次实验。搭建风水互补微电网的功率波动节能控制数学建模仿真实验平台。
假设选取的微电网系统中有2台风力发电机组和2台水力发电机组和容量为50 kM的蓄电池,忽略蓄电池的充放电损耗,选择秋季的某天作为仿真时间,分别利用传统算法与改进算法进行风水互补微电网的功率波动节能控制数学建模实验,将不同算法进行建模的各个微源的单位发电、运行额外维护成本数据与实际的数据相比较,以此来衡量改进算法的节能控制有效性。对比结果见表1—表3。

表1 各微源发电成本和额外维护成本Tab. 1 Cost of each micro source power generation and cost of additional maintenance
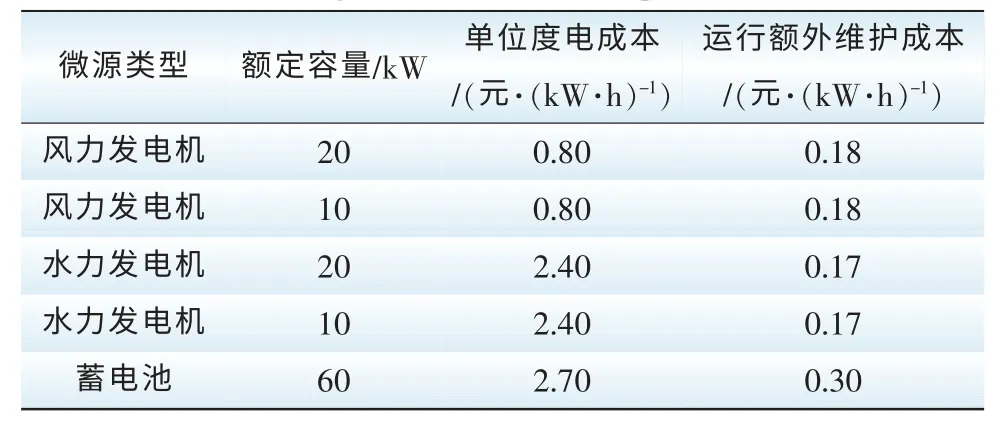
表2 传统算法的发电成本和额外维护成本Tab. 2 The generation cost and additional maintenance cost by the traditional algorithm

表3 改进算法的发电成本和额外维护成本Tab. 3 The generation cost and additional maintenance cost by the improved algorithm
从表1—表3可以得出,改进算法建立的风水互补微电网的功率波动节能控制数学模型的节能控制效果要优于传统算法,主要是因为改进算法针对运行的风水互补微电网系统进行分析,先计算出系统在不同自然条件下所需要的发电最大功率,依据系统在不同条件下对功率的需求设置2条或多条发电机机外特性曲线,在此基础上将风水互补微电网的功率波动节能控制问题转换为发电机与其功率平衡控制的问题,在保证负荷需求的基础上,以最大化利用风能和水能为原则,以整个系统的运行发电成本最低为目标建立风水互补微电网的功率波动节能控制数学模型。
上述实验可以证明,基于功率曲线算法的风水互补微电网的功率波动节能控制数学建模方法建模精确度高,鲁棒性强。
4 结语
针对采用当前的算法进行建模时受到大量的外界因素干扰,造成功率波动节能控制效果不佳的问题,提出了一种基于功率曲线算法的风水互补微电网的功率波动节能控制数学建模方法。该方法针对运行的风水互补微电网系统进行分析,先计算出系统在不同自然条件下所需要的发电最大功率,依据系统在不同条件下对功率的需求设置2条或多条发电机机外特性曲线,在此基础上将风水互补微电网的功率波动节能控制问题转换为发电机与其功率平衡控制的问题,在保证负荷需求的基础上,以最大化利用风能和水能为原则,以整个系统的运行发电成本最低为目标建立风水互补微电网的功率波动节能控制数学模型。实验仿真证明,基于功率曲线算法的风水互补微电网的功率波动节能控制数学建模方法建模精确度高,鲁棒性强。
[1] 高原,赵贺雄. 微电网控制策略研究[J]. 中国科技博览,2013(38): 261-261.GAO Yuan,ZHAO Hexiong. Micro grid control strategy study[J]. China Science and Technology Review,2013(38): 261-261(in Chinese).
[2] 王波. 互补储能技术及其控制策略[J]. 电力与能源,2014(6): 764-767.WANG Bo. Complementary energy storage technology and its control strategy[J]. Electric Power and Energy,2014(6): 764-767(in Chinese).
[3] 万航羽,吴政声,丛翔宇,等. 云南省风水互补协调运行探讨[J]. 现代制造,2013(27): 25-27.WAN Hangyu,WU Zhengsheng,CONG Xiangyu,et al. in yunnan province,feng shui complementary harmoniously study[J]. Modern Manufacturing,2013(27): 25-27(in Chinese).
[4] 王成山,于波,肖峻,等. 平滑微电网联络线功率波动的储能系统容量优化方法[J]. 电力系统自动化,2013,37(3): 12-17.WANG Chengshan,YU Bo,XIAO Jun,et al. Smooth micro grid tie line power fluctuations in energy storage system capacity optimization method[J]. Automation of Electric Power Systems,2013,37(3):12-17(in Chinese).
[5] 陈秋南,韦钢,卢炜,等. 基于超级电容器控制策略的含风电微电网电压波动的抑制[J]. 电力系统保护与控制,2014(16): 96-102.CHEN Qiunan,WEI Gang,LU Wei,et al. Based on the control strategy of the super capacitor micro power grid containing wind power voltage fluctuation suppression[J].Power System Protection and Control,2014(16): 96-102(in Chinese).
[6] 贾书杰,徐建源,朱钰,等. 风电场的功率波动对电网电压稳定性影响研究[J]. 东北电力技术,2013,34(2):15-18.JIA Shujie,XU Jianyuan,ZHU Yu,et al. Wind power fluctuation influence to power grid voltage stability study[J].Journal of Northeast Electric Power Technology,2013,34(2): 15-18(in Chinese).
[7] 王晓东,张磊,姚兴佳,等. 考虑储能电池SOC状态的风电场功率波动抑制控制[J]. 电源学报,2014,12(2):73-77.WANG Xiaodong,ZHANG Lei,YAO Xingjia,et al. To consider the state of the energy storage battery SOC wind power fluctuations inhibitory control[J]. Journal of Power,2014,12(2): 73-77(in Chinese).
[8] 洪海生,江全元,严玉婷. 实时平抑风电场功率波动的电池储能系统优化控制方法[J]. 电力系统自动化,2013,37(1): 103-109.HONG Haisheng,JIANG Quanyuan,YAN Yuting. Realtime control battery energy storage system optimization control method of wind power fluctuations[J]. Automation of Electric Power Systems,2013,37(1):103-109(in Chinese).
[9] 周银,林桦. 平滑永磁同步风电系统功率波动的改进最佳转矩控制策略[J]. 电力系统自动化,2013,37(9): 13-17.ZHOU Yin,LIN Hua. Smooth power fluctuation of permanent magnet synchronous wind power system to improve the optimal torque control strategy[J]. Automation of Electric Power Systems,2013,37(9): 13-17(in Chinese).
[10] 张栋华,李征,蔡旭. 基于量子行为粒子群算法的微电网优化配置[J]. 计算机仿真,2014,31(8): 120-124.ZHANG Donghua,LI Zheng,CAI Xu. Particle swarm optimization(pso)algorithm based on quantum behavior of micro grid optimization configuration[J]. Computer Simulation,2014,31(8): 120-124(in Chinese).

