直流逆变站动态无功源的电压稳定控制优化
赵鹏,李杰
(黄河水利职业技术学院 自动化工程系,河南开封 475004)
近几年来,随着经济的快速增长,电力系统的发展速度突飞猛进,但也给电力系统的安全问题带来了新的隐患,直流逆变站电压稳定控制就是其中之一。电压稳定性已经成为威胁电力系统的主要因素,在对电压控制的过程,主要是对负荷进行控制[1-2]。因此,可以预见,在未来相当长的一段时间内,电流负荷问题会是供电系统内的一个新的挑战,并且严重性还会与日俱增[3-5]。
文献[6]研究交直流并联系统动态电压稳定,但受小干扰特征分析法限制,研究结论仅适用于混联电网小扰动电压失稳模式鉴别。文献[7]采用基于直流系统和交流系统方程分解求解的崩溃点法,分析交直流联合系统的电压稳定问题。文献[8]是一种直流逆变站为动态无功源的电压稳定控制方法,该方法首先建立直流受端交直流混联电网仿真模型,评估受端电网暂态稳定性并设置控制参数,循环测量逆变站高压母线电压并判断是否满足控制启动判据和持续时间的要求来进行电压稳定控制,但存在控制时间较长,稳定性较差的问题。目前,我国使用的直流逆变站动态电压稳定系统主要是来自欧美国家的控制方法,在对直流逆变站电压调节过程中,对电压崩溃导致电压不稳和功角失恒导致电压不稳的情况不能及时计算出结果,导致电压调节稳定时间较长。如果不能及时解决问题,势必导致上一级供电系统电压不稳,严重情况会将整个供电网络拖垮,最终发展成为电压崩溃。
针对上述问题的产生,提出一种直流逆变站动态无功源的电压稳定控制方法,通过建立动态负荷模型,对直流逆变站输电和配电系统的动态电压控制,及时发现电压无功源振荡阻尼,进行动态模型参数修正暂态稳定控制和电压闪变控制。降低了系统对电压稳定调节时间。仿真实验表明,动态无功源电压稳定控制方法缩短了直流逆变站电压动态调节时间,改善动态调节过程,使系统震荡得到有效控制,负荷电压稳定,符合应用要求。
1 无功源电压稳定控制过程分析
无功源稳定是指负荷电压随着电网逆变站内电压变换的频率而相应产生有规律的波动,对控制电压的稳定有着重要影响。
1.1 电网动态负荷模型
在无功源电网电压稳定控制的情况下,一般采用动态负荷模型。多项式负荷模型如式(1)所示。

式中:A1,A2,A3,A4,B1,B2,B3,B4为系数。
换一个方程式表达为:

Δf=f-f0,ap+bp+cp=1,aq+bq+cq=1,U和f为标么值。在无功源电力系统计算中,可以忽略频率的影响,因此,上述方程可以简化为:

当ap=bp=aq=bq=0,cp=cq=1时,与此同时,无功源电压负荷模型转化为恒功率模型,在无功源电压恒功率计算中经常采用。
1.2 电网动态负荷模型参数的修正
在动态无功源电压稳控中进行负荷模型参数的修正,主要利用插值的原理,在无功源的电压稳态运行点对动态负荷模型参数线性化,按照持续插值方法,在动态无功源电路系统中对原参数不断动态修正,以达到电压稳定控制更接近要求。电力系统中负荷元件表达为:

负荷的基本特点就是可以在无功源电压系统中随着电压变化而变化。因此,可以分为频率特性和电压特性。在直流逆变站中通常又有静态和动态两大特性。他们本质在于对电压进行稳定过程中,对电压进行复制的大小不同,系统的干扰程度不同。因此负荷动态模型用公式表示为:

动态负荷模型反应的是动态电压的特性,尤其是低电压条件下,动态电压特性从根本上决定了对电压系统稳定控制的行为方法。
式(5)中p0和Q0是负荷侧无功源动态电压的初始值,U负荷电压的标么值,其物理意义无功源动态对电压变化率,即。
在对电压稳定控制时求偏导数,并把偏导数动态在p处线性化,在稳定控制电压的同时,ΔU来修正p,以达到稳定控制效果。
在直流逆变站动态无功源电压动态修正负荷模型进行参数调节时,参数p和Q均为电力系统在正常负荷状态的特征系数。建设一个精确的直流逆变站动态无功源电压稳定负荷模型,尤其是当直流逆变站电压偏离标准较多时,能很好地反应,以便达到稳定控制特性。
根据动态稳控特性和电压系数p,对式(5)在直流逆变站动态无功源电压在额定值附近求偏数,得公式如下:
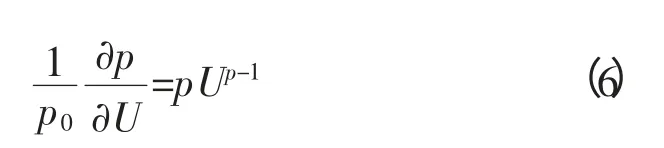
式中:p0为直流逆变站初始节点;p为初始节点无功源功率;U为直流逆变站动态无功源电压标幺值。式(6)表示直流逆变站在无功源电压稳定过程中,电压变化为ΔU时,p会相应发生变化。因此,利用持续性插值原理,根据电压稳定过程中节点调节(1-mΔU),提出动态修正计算方法来调整电压变化,进行稳定。调节参数用公式表示为:

pmn不是固定数值,它会随着逆变站直流电压变化而变化,在直流逆变站初始电压时,电压调整系数不运行,当电压超出额定范围后,动态无功源修正量与负荷开始运行,把计算进行简化后得到参数,用公式表示为:
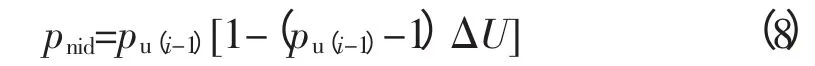
同理,当直流电压从无功源额定值发生变化至(1-mΔU)时,得到相似公式pnid=qu(i-1)[1-ΔU+qu(i-1)ΔU] 。对以上公式进行推导,得到在直流逆变站动态电压的修正参数公式:

式中:pi和Qi为直流逆变站中第i个节点;U无功源电压实时值,以上参数均为标幺值。
2 直流逆变站动态无功源的电压稳定控制
控制电压的本质是控制负荷保持稳定。在直流逆变站动态无功源的电压控制中,负荷的特征具有特别重要意义。
2.1 直流逆变站电压调整
无功源电压的无功特性是调整电压的关键。由于直流逆变站存在较大电流,使无功源在输送过程损失,因此 在直流逆变站中对无功源进行补偿。
负荷补偿装置对电压调整的表达式为:
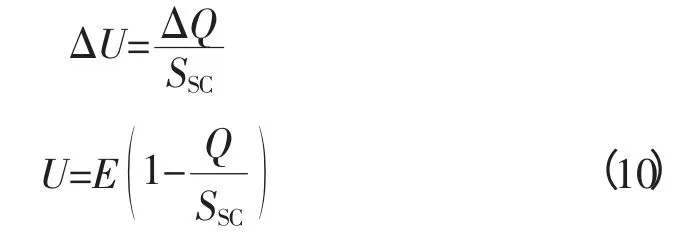
式中:ΔQ为直流逆变站对无功源电压提供的补偿;SSC为在直流电压中接入点的电流量;U为逆变站对无功源补偿后的负荷线电压。由于无功源对直流逆变站传输补偿比较困难,无功源的大量传输会给直流逆变站带来较大压力,如直流逆变站相角差较大,各线路两端电压相角都会增大。根据电力系统对直流逆变站线路要求,两端电压要维持在(1±5%)pu的安全范围内,因此,优先考虑就地补偿。
2.2 无功源电压稳定控制
无功源补偿器是并联连接动态发生器,输出补偿可以要求直流逆变站电压实时调节。其主要构件有:SR饱和电控制装置,TCR晶闸管管制电抗装置,TSC晶闸管开关电抗装置,TCT可控变压器,SCCC/LCC自换限换整流装置。
以上构件组成SVC控制系统,当直流逆变站电压超出额定功率,TCR就进行限额,抵消无功源消耗。
无功源控制为直流逆变站动态无功源电压提供必要的输入信号,根据不同的电压负荷,计算出结果进行输出,其结果主要包括,三相平衡控制,直流电压无功源控制和阻尼辅助控制。
在直流逆变站中,通过测量不同环节电路系统产生一个负荷补偿无功源的输出量,SVC会根据不同场合,对各环节提供必要的控制。具体设计如图1所示。

图1 无功源电压调节器Fig. 1 Reactive power source voltage regulator
无功源支持直流逆变站无功源电压所补偿的节点近似数,系统作为一个等值负荷,通过控制器并入电压控制系统。当系统连接电压母线高于U时,系统进行无功源平衡,消耗系统功率,使电压下降。反之,电压过低时,控制器引发无功源参考电压,无功源进行容性负荷,向直流逆变站发出无功源,调节电压上升。调节原理如图2所示。

图2 直流逆变站无功源电压控制原理图Fig. 2 Principle diagram of DC inverter station reactive power source voltage control
无功源的数学模型用公式表示为:

动态补偿无功源电压用公式表示为:

根据系统的无功源电压补偿公式,可以计算出无功源伏安特曲线图,如图3所示。
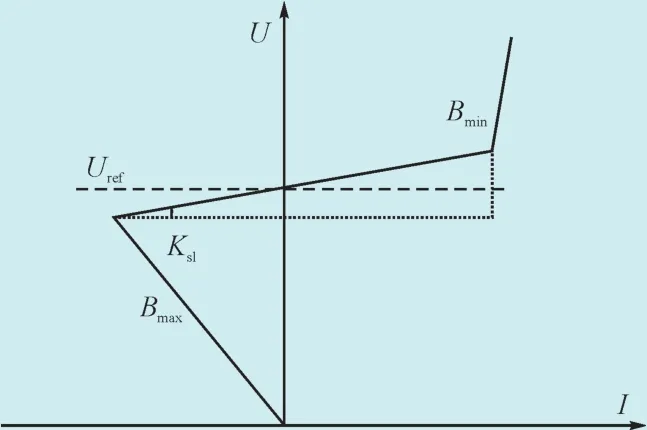
图3 无功源伏案特曲线图Fig. 3 The reactive power volt-ampere characteristic curve
无功源在直流逆变站的电压调节中,补偿装置在线形控制区域内运行,直流电压增量与无功源电压增长量之比可用斜率ksj来表示:

在直流逆变站中斜率保持在1%~11%之间,经典值为3%~6%。
3 仿真实验
为了证明直流逆变站动态无功源电压稳定控制的效果,以及对直流逆变站的电压稳定控制程度,采用传统的动态无功源的电压稳定控制方法与本文方法进行仿真实验。
在IEEE14节点直流逆变站系统中,根据模态分析动态无功源电压调节器安装位置,并根据电流容量得到相应参数。整个直流逆变站节点容量为370.66 MV·A,线路内电压维持在(1±5%)pu范围内,直流逆变站14-13靠近母线,经6个周期0.12 s后故障消失,直流逆变站恢复初始条件正常运行,仿真实验8 s结束。仿真输出结果如下。
通过仿真输出图4—图6可以看出,直流逆变站对维持负荷电压有积极作用,同时发电机功角振荡得到抑制,在短时间内恢复初始运行。直流逆变站动态无功源电压调节时间与负荷电压情况如下所示。
根据图7、图8可知,当实验次数一定时,改进方法所需调节时间相比传统方法缩短了3 s,改进方法的负荷电压相比传统的负荷电压要稳定很多。

图4 动态无功源电压调节曲线Fig. 4 The dynamic reactive power source voltage adjustment curve

图5 考虑负荷动态特性调节曲线图Fig. 5 Adjustment curve considering load dynamic characteristics
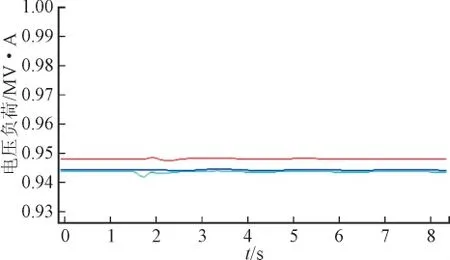
图6 动态无功源电压调节发电机功角曲线图Fig. 6 Power angle curve of the dynamic reactive power source voltage regulating generator

图7 电压调节时间分析图Fig. 7 Voltage regulation time analysis diagram
综上所述,直流逆变站动态无功源电压稳定控制明显改善,系统震荡有效抑制,对负荷影响减弱。
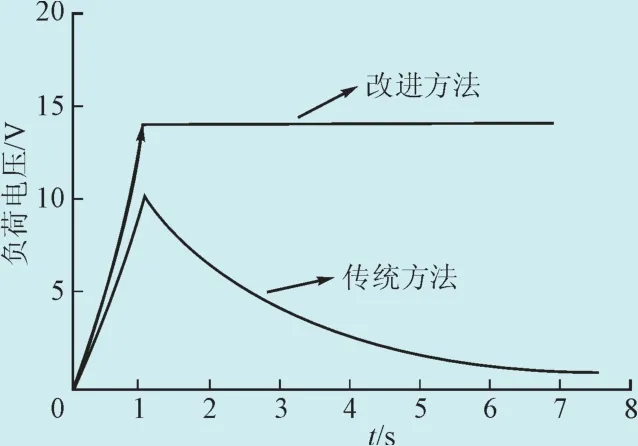
图8 负荷电压分析图Fig. 8 Load voltage analysis diagram
4 结论
提出一种直流逆变站动态无功源的电压稳定控制方法,通过建立动态负荷模型,对直流逆变站输电和配电系统的动态电压控制,及时发现电压无功源振荡阻尼,进行动态模型参数修正和暂态稳定控制和电压闪变控制。提高系统对电压稳定调节时间。仿真实验表明,动态无功源电压稳定控制方法缩短了直流逆变站电压动态调节时间,改善了动态调节过程,系统震荡得到抑制,负荷电压稳定,符合应用要求。
[1] IEEE/CIGRE Joint Task Force on Stability Terms and Definitions. Definition and classification of power system stability [J]. IEEE Transactions on Power Systems,2004,19(2):1387-1401.
[2] IEEE Task Force on Load Representation for Dynamic Performance,System Dynamic Performance Subcommittee,Power System Engineering Committee. Standard load modelsfor power flow and dynamic performance simulation[J].IEEE Transactions on Power Systems,2005,10(3).
[3] DANLEL KARLSSON,DAVID J. HILL. Modeling and identification of nonlinear dynamic loads in powersystem[J].IEEE Transactions on Power System,2004,9(1):157-166.
[4] Sameh Kamel Mena Kodsi,ClaudioA. Canizares. Modeling and simulation of IEEE 14 bussystem with FACTS controllers[J]. Technical Report #2003-3.
[5] AVRON H,SHKLARSKI G,TOLEDO S. Parallel unsymmetric-pattern multifrontal sparse LU with column preordering[J]. ACM Transactions on Mathematical Software,2008,34(2).
[6] NACHTIGAL N M. A look-ahead variant of the lanczos algorithm and its application to the quasi-minimal residual methods for non-hermitian linear systems,PhDthesis,MIT,Cambridge,MA,2003.
[7] ASHCRAFT C,GRIMES R. On vectorizing incomplete factorizations and SSORPreconditioners[J]. SIAM Journal of Scientific and Statistical Computing,2008(9):122-151.
[8] AVRON H,SHKLARSKI G,TOLEDO S. Parallel unsymmetric-pattern multifrontal sparse LU with column preordering[J]. ACM Transactions on Mathematical Software,2008,34(2).

