考虑受端励磁系统的交直流稳定性分析
李雪亮,张杰,王云鹏,杨金洪,韩学山,孙东磊,高效海
(1. 国网山东省电力公司经济技术研究院,山东济南 250021;2. 电网智能化调度与控制教育部重点实验室(山东大学),山东 济南 250061)
高压直流输电以其传输容量大,远距离输电以及连接不同频率的电网等优势,近几年得到快速发展。我国已经形成了交直流混合格局,与此同时,受端系统的电压支撑对高压直流输电稳定运行的影响引起关注[1-2]。
直流受端系统与逆变站的工作状态紧密相联,存在同步问题,表现为受端母线的电压稳定性[3-4]。在以往的研究中,假定受端系统的参数不发生改变,而研究直流输电的特性,如直流输电能力以及受端母线电压的稳定性。文献[5]中基于直流电流提出最大输送功率曲线,并说明受端系统短路比对其的影响;文献[6]中研究直流输电控制方式对受端母线电压稳定性的影响并提出相应判定指标。然而,在实际运行中,交直流混合系统更多地受到交流系统故障或者运行方式的变化等的影响[7-9],从而威胁系统的稳定运行。
针对交流系统运行状况的改变对交直流的同步运行的影响,一般将受端系统进行简化等值。目前来说,对受端系统的等效有两类:一类假定受端交流系统的运行方式固定,戴维南等值电路参数随之固定,如等效电势E、等值阻抗Z[5-6],虽能实时地等值受端网络,但是在描述直流输电特性上却忽略了受端的支撑能力;一类戴维南等值电路的参数固定,受端母线带有变动的负荷动态地模拟受端[10-11],虽然体现了受端的变化特性,却不能真实地反映实际系统。为了体现受端励磁系统的调节作用以及其运行行为的变化,文献[12]在文献[5-6]的基础上,考虑受端的励磁系统,继而描述直流输电特性,包括最大功率曲线以及受端母线电压稳定性,但却未考虑其励磁达到极限时可能产生的影响。
传统负荷节点电压稳定的研究中,也有不少考虑了励磁约束的影响,如文献[13]采用光滑函数对励磁器的限制作用进行模拟,当考虑励磁饱和环节后,负荷节点电压的运动轨迹发生变化。文献[14]以一个典型的电力系统模型为基础,分析了考虑励磁限制所导致的各种分岔行为。文献[15]采用IEEE14节点网络数据,研究了发电机最大励磁限制对系统电压稳定性的影响。直流输电作为受端的一个特殊负荷,其受端发电机励磁约束对其运行的稳定性影响不可忽视。
本文的主要工作在于,考虑受端发电机的励磁系统及其约束,通过扩展的交直流潮流[16-20]以及受端系统的戴维南等值[21-24],在传统的直流输电的最大功率曲线以及电压稳定指标基础上发展,继而分析直流输电的运行特性,并对受端系统的电压支撑能力做一个说明。最后,通过算例分析对本文观点进行有效性验证。
1 交直流输电系统的等值模型
为了研究直流输电受端系统的电压稳定,本文模型聚焦于逆变站侧。
1.1 逆变侧等值模型
直流输电系统的逆变侧等值模型如图1所示,受端系统用戴维南参数等值,受端系统的励磁作用在随后的模型中会体现,其数学表达如下[2]:

图1 直流输电系统换流站简化模型Fig. 1 Simplified model of an HVDC converter station


式中:Pd为逆变器向交流系统输送的有功功率;Qd为逆变器从交流侧吸收的无功功率;Id为直流电流;Vd为直流电压;γ为关断角;μ为换相角;Pac、Qac分别为母线向受端交流系统输送的有功功率、无功功率;Bc为交流滤波器和无功补偿电容的等效导纳;Qc为等效电容器补偿的无功功率;V、δ分别为母线处电压幅值和相角;E、准、|Z|、θ分别为受端系统的戴维南等值电势幅值及相角、等值阻抗模值、等值阻抗角;K为换流器变压器参数与直流系统标准值有关的常数;C为与换流器变压器参数与直流有关的2个常数,其中C的表达式如式(10)所示。

式中:ST为变压器的容量;Uk%为变压器的短路电压百分比;τ为变压器的变比。
1.2 直流输电控制方式
在研究直流输电受端稳定性时,本文不考虑送端的电压。换流器的控制方式有多种,本文只考虑送端整流器定电流(或定功率),受端逆变器定熄弧角或定电压控制方式。
1)定电流控制方式:给定Id;
2)定功率控制方式:给定Pd;
3)定熄弧角控制方式:给定γ;
4)定电压控制方式:给定Ud。
2 考虑励磁系统的扩展潮流
本文不考虑调速系统的作用,不限制各发电机的有功出力情况,也就是不考虑系统频率的变化,即二次调频后频率无误差调节。系统潮流是扩展潮流,考虑受端的励磁系统及其达到极限后。
2.1 IEEE-I 励磁模型
发电机端电压受励磁系统控制,本文采用IEEE I型励磁系统,如图2所示,不考虑其暂态性能,只考虑其稳态模式,其模型如下:

图2 IEEE I型励磁调节器Fig. 2 IEEE I-type excitation regulator

式中:VRmin、VRmax分别表示励磁系统限幅环节上下限。
不考虑调速系统,同步发电机的输出功率模型如下所示:

式中:Pgi、Qgi为同步发电机i有功、无功出力;Xdi、Xqi及δi为发电机i的d、q轴同步电抗及功角;KAi为励磁调节器放大环节的放大倍数;KEi为励磁机的励磁系数;Vi和θi为发电机机端节点电压幅值和相角。其中δi、θi与第1.1节中的等值模型的δ、θ加以区分,避免符号的混乱性。
2.2 扩展潮流
假设系统节点数为n,发电机节点为m,其中有平衡节点,传统网络的方程为:

式中:若节点i连接发电机,Pgi、Qgi为式如式(15)所示;若节点i不连接发电机,Pgi=0,Qgi=0。若节点i为直流输电的受端母线节点,则Pdi、Qdi如式(1)、式(2)所示;若节点i为交流节点,Pdi=0,Qdi=0。PLi、QLi分别表示负荷节点的有功功率和无功功率。Gij、Bij分别表示节点i、j的电导、电纳。
不计阻尼系数,经二次调频后,频率与参考频率相同,发电机对应节点的原动机有功功率平衡表达式为:

式中:Pgsi为扩展潮流的控制量;Pgi为各发电机对应节点的原动机输出功率。
状态量为n个节点的电压幅值和除平衡节点的n-1个节点电压相角以及m个发电机功角,因此未知量的个数为2n+m-1。传统网络方程个数为2n,发电机节点除平衡节点外,原动机的有功功率平衡方程为m-1个,系统功率平衡方程总数为2n+m-1,可联立求解2n+m-1个状态量。
2.3 励磁约束的处理
同步发电机转子电流的约束用AVR输出VRi来表达,如果忽略励磁系统的饱和作用,在稳态时AVR 的输出电压VRi正比于发电机的转子电流。因此,转子电流达到最大值时,等价于AVR 的输出电压VRi达到最大值VRi,max并保持不变,即式(15)中的KAi·(Vrefi-Vi)用VRi,max替代。
励磁达到极限时,并未改变状态量,因此雅克比矩阵调整的只是元素偏导数的表达式。
2.4 求解流程
本文扩展潮流的求解的具体流程如图3所示,其中励磁处理框如第2.3节所示。
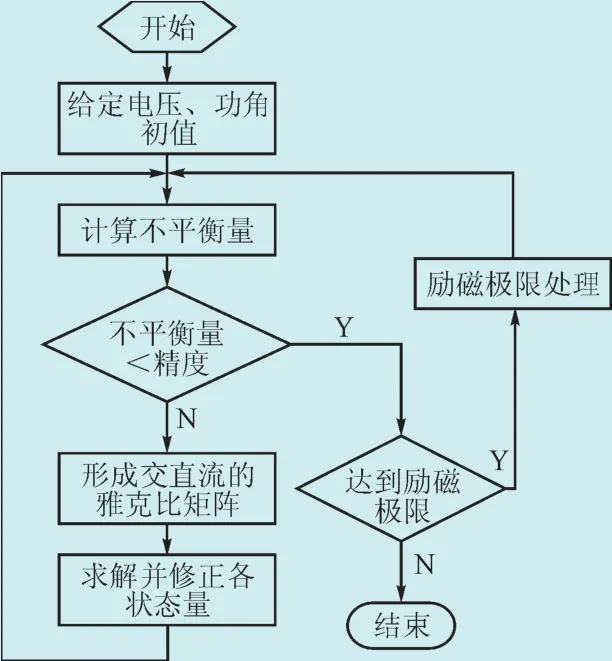
图3 模型求解流程图Fig. 3 Solution flow chart of the model proposed
3 算例分析
3.1 算例1

图4 考虑受端励磁的交直流输电系统换流站简化模型Fig. 4 Simplified model of an HVDC converter station of an AC /DC system considering excitation voltage control
算例1为单机受端系统,如图4所示,考虑其励磁系统,与图1有差别。为了确定交直流输电系统的参数,参考文献[5-6],设额定状态下参数如下(取标么值):Vdn=1,Idn=1,γn=18°,Pgn=1,cos 准=0.9。其他参数:Z=1/3,θ=90°,Uk%=18%,τ=1,除了式(1)—(9)外,还包括式(15),以及发电机端节点的功率平衡方程。
3.1.1 受端励磁对交直流母线电压影响
在额定状态下,通过式(1)得到μ,额定状态下,Qdn=Qcn,得出补偿电容Bc;通过式(3)得到K,取θ=90°,通过式(5)、式(6)得到E、δ;计算Pca、Qca,额定状态下发电机端电流Ig为I∠0°,Pg=EIcos 准,由此式计算得到Ig;取励磁参数Ka=50,Ke=1,Xd=0.249 5 pu,Xq=0.237 pu,由式(15)以及机端功率平衡方程得到参考电压Vref以及初始负荷PLn、QLn。
随着PL、QL按恒功率因数tan φ=0.85增加,直流系统运行在恒电流Id=1 pu,恒熄弧角γ=18°,进行潮流计算,PL=9 pu,步长为0.2,进行5次潮流计算得出发电机的励磁机的励磁电压VR及直流相关参数见表1。

表1 励磁充裕下励磁电压以及直流参数随负荷的变化Tab. 1 Excitation voltage and DC parameters with varying load in an ample excitation condition pu
从潮流计算中可以看出,负荷增加时受端的发电机励磁需要不断增加,端电压降低,直流输送的功率降低,当发电机的励磁到达VRmax=3.6,模拟其对直流输电的影响,如表2所示。

表2 励磁受限时励磁电压以及直流参数随负荷的变化Tab. 2 Excitation voltage and DC parameters with varying load in the limited excitation condition pu
由表2可以看出,当发电机的励磁受到限制时,受端母线电压持续升高并且速度特别快,快超过限值1.1,系统的安全性受到极大的威胁。
在发电机励磁受限时,随着负荷的变动直流输电受端母线电压不稳定。实际上也就是励磁状况影响了受端系统的戴维南等值参数,进而影响直流输电的运行状态。而传统分析中,只是按照图1改变等参数观察其对直流输电的影响。励磁是影响戴维南E、Z等值的关键一环,观察上述2种情况下戴维南参数的对比,如表3所示。
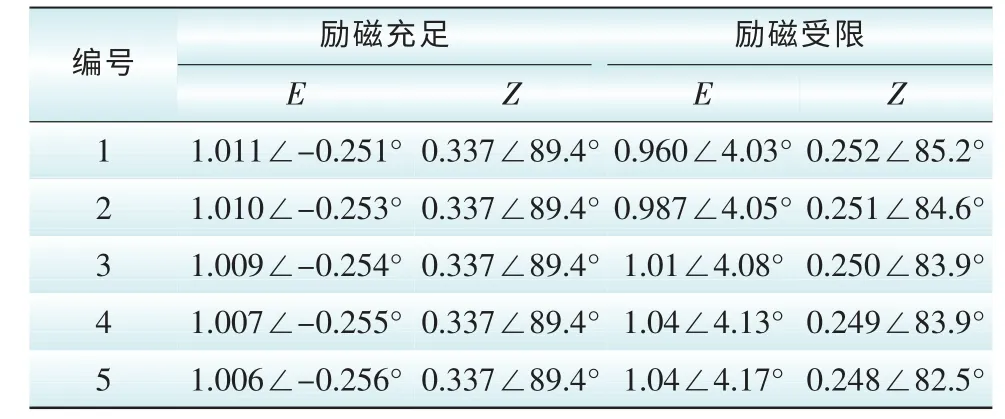
表3 2种状况下戴维南等值参数Tab. 3 Thevenin parameters in two conditions pu
从表3中可以看出,励磁受到限制时,一定的直流输送时,受端负荷增加,戴维南等值电势升高,电抗变化不大。
3.1.2 受端励磁对输电能力的影响
按3.1.1中方法计算,保持初始负荷,取Ka=50,Ke=1,Xd=0.25 pu,Xq=0.2 pu,改变直流电流Id的值,按照文献[3]作出最大功率曲线,如图5所示。

图5 Pd随Id的变化曲线Fig. 5 Curves of Pd versus Id
通过对比曲线1、2可以看出,励磁的作用还是限制了直流输电系统的最大可输送功率;对比曲线2、3可以看出,励磁受限导致直流输送功率降低。曲线3对比3.1.1可以发现,励磁受限值的大小以及系统的运行状态影响其对直流输电的作用。
3.2 算例2
以IEEE 39节点系统为例,参考文献[25],将23-24线路改为直流线路,但是与之不同的是,节点23并联1.5 pu的电容,节点24并联2 pu的电容,节点23设为负荷节点,新增负荷P=5.04 pu,Q=2.5 pu;节24点设为直流的落入点,Id=4.16 pu,Ud=1.21 pu,控制方式为定电流定电压控制,同时去除其所带负荷。为了研究方便,设置受端系统发电机的动态参数如表4所示。

表4 节点39系统动态元件参数Tab. 4 Parameters of dynamic elements in 39 nodes system
结合全网负荷递增的连续潮流,所有负荷节点的功率按初始的功率因数成比例增加,各发电机平均分担增加的负荷,发电机仅受励磁系统的限制。
励磁系统受限时,对交直流混合节点的电压幅值还是有影响的。随着全网负荷的增加,发电机励磁受限情况见表5、混合节点的电压幅值见表5。
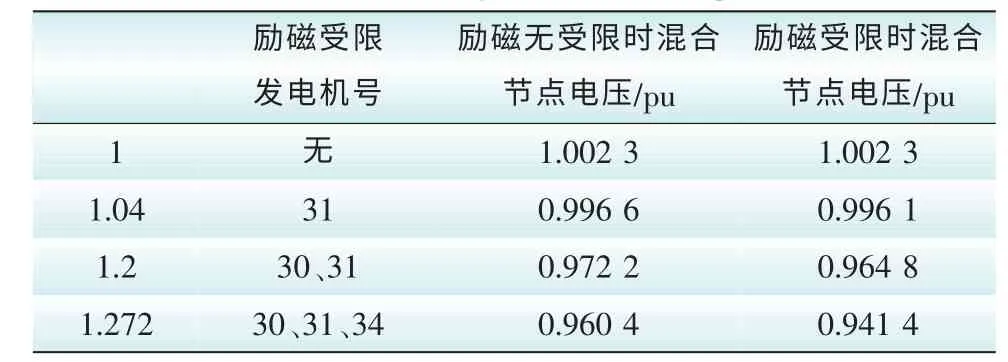
表5 发电机励磁系统状态表Tab. 5 Excitation system state of generators
对比图6中曲线1、2可以发现,有励磁限制时,直流受端节点电压幅值下降快,不利于其电压稳定性。
受端系统的支撑作用不仅与受端负荷水平有关,还与发电机的励磁相关。评价指标SCR仅是受端系统的电压支撑能力的一个外在表现,其支撑作用与励磁紧密联系。
4 结语
随着新能源的加入以及远距离输电的迫切需求,直流输电比例增大,其受端系统对其的支撑作用研究意义重大。对此,基于扩展潮流以及戴维南等值方法,本文分析了受端发电机励磁系统对直流输电的影响,评价了直流输电的受端节点电压以及输送能力,指出受端系统的支撑作用依赖于发电机的励磁系统,发现其励磁受限时直流输电的安全稳定性受到威胁。本文基于的是单馈入的交直流输电模型,并未考虑多馈入直流系统,研究将会在多馈入交直流系统中继续深入。

图6 不同励磁限值时受端节点电压Fig. 6 Voltage of receiving point with different excitation voltage limits
受端支撑作用能力强弱影响直流输电的安全稳定性,而支撑能力与励磁系统以及负荷紧密相关。传统意义上支撑能力由戴维南等值参数的阻抗表示,文中未能深入探讨励磁系统与阻抗的关系,未能提出与励磁相关的评价的指标,希望未来能对此提出新的观点。
[1] 刘振亚.特高压电网[M]. 北京:中国经济出版社,2005:27.
[2] 徐政. 交直流电力系统动态行为分析[M]. 北京:机械工业出版社,2004.
[3] 王艳,李磊,王葵. 直流联网工程对电网暂态稳定性的影响[J]. 电网与清洁能源,2008,24(10): 9-11.WANG Yan,LI Lei,WANG Kui. Influences of DC interconnection on power grid transient stability[J]. Power System and Clean Energy,2008,24(10): 9-11(in Chinese).
[4] 常勇,李辉,梁云丹. 面向电网稳定性的智能化直流输电控制系统[J]. 电网与清洁能源,2012,28(6): 1-7.CHANG Yong,LI Hui,LIANG Yundan. Power gridoriented stability multi-agent DC power transmission control system[J]. Power System and Clean Energy,2012,28(6): 1-7(in Chinese).
[5] 徐政. 联于弱交流系统的直流输电特性研究之一—直流输电的输送能力[J]. 电网技术,1997,1(1): 12-16.XU Zheng. Characteristic of HVDC connected to weak AC systems part1: HVDC transmission capability[J]. Power System Technology,1997,21(1): 12-16(in Chinese).
[6] 徐政. 联于弱交流系统的直流输电特性研究之二——控制方式与电压稳定性[J]. 电网技术,1997,21(3):1-9.XU Zheng. The Characteristics of HVDC systems to weak ac systems part II: control modes and voltage stability[J].Power System Technology,1997,21(3):1-9(in Chinese).
[7] 董凌,许德操. 青藏直流联网工程负荷特性对短路电流计算影响的分析[J]. 电网与清洁能源,2010,26(12):57-61.DONG Ling,XU Decao. Researches on the load representation of Qinghai-Tibet power grid AC/DC system[J]. Power System and Clean Energy,2010,26(12): 57-61(in Chinese).
[8] 余海翔,陈立,梁家豪. 天广直流广州换流站换相失败机理探讨[J]. 高压电器,2015,51(3): 151-154.YU Haixiang,CHEN li,LIANG Jiahao. Investigation of commutation failure in guangzhou converter station of Tian-Guang HVDC project [J]. High Voltage Apparatus,2015,51(3): 151-154(in Chinese).
[9] 陈干,田方,刘宁. 高压直流输电工程换相失败研究[J].高压电器,2015,51(7): 136-140.CHEN Gan,TIAN Fang,LIU Ning. Research on HVDC transmission project commutation failure[J]. High Voltage Apparatus,2015,51(7): 136-140(in Chinese).
[10] 肖俊,李兴源. 考虑交流系统负荷模型的直流输电特性分析[J]. 电网技术,2013,37(9): 2410-2415.XIAO Jun,LI Xingyuan. Analysis on characteristics of HVDC power transmission system in AC/DC hybrid system considering load model of AC system[J]. Power System Technology,2013,37(9): 2410-2415(in Chinese).
[11] 赵贺,周孝信. 受端系统负荷对高压直流输电的影响[J].中国电机工程学报,2007,27(16): 1-6.ZHAO He,ZHOU Xiaoxin. Influence of reactive end load on HVDC transmission[J]. Proceeding of the CSEE,2007,27(16): 1-6(in Chinese).
[12] AIK Denis Lee Hau,ANDERSON G. Quasi-static stability of HVDC systems considering dynamic effects of synchronous machines and excitation voltage control[J]. IEEE Trans on Power Delivery,2006,21(3): 1501-1514.
[13] 李国庆,张浩,李江,等. 基于分叉理论研究励磁饱和环节对系统电压稳定的影响[J]. 电力系统自动化设备,2015,35(3): 1-5.LI Guoqing,ZHANG Hao,LI Jiang,et al. Influence of excitation saturation element on power system voltage stability based on bifurcation theory[J]. Electric Power Automation Equipment,2015,35(3): 1-5(in Chinese).
[14] 王庆红,周双喜. 考虑励磁限制的典型三节点电力系统分岔分析[J]. 华北电力大学学报,2004,31(1): 5-10.WANG Qinghong,ZHOU Shuangxi. Bifurcation analysis with excitation limit in classic three-node power system[J].Journal of North China Electric Power University,2004,31(1): 5-10(in Chinese).
[15] 臧洋. 基于分叉理论的电力系统电压稳定性研究[D]. 北京:华北电力大学,2005.
[16] 赵晋泉,钱天能. 计及发电机励磁电流约束和电枢电流约束的连续潮流[J]. 中国电机工程学报,2012,32(22):118-125.ZHAO Jinquan,QIAN Tianneng. The continuous power flow considering both generator excitation limits and armature current limits[J]. Proceeding of the CSEE,2012,32(22): 118-125(in Chinese).
[17] 王庆红,周双喜,胡国根. 基于扩展潮流模型的电力系统电压稳定分析[J]. 电网技术,2002,26(10): 25-29.WANG Qinghong,ZHOU Shuangxi,HU Guogen. Power system voltage stability analysis using expanded power flow models[J]. Power System Technology,2002,26(10): 25-29(in Chinese).
[18] TYLAVSKY D J. A simple approach to the solution of the AC- DC power flow problem[J]. IEEE Trans on Education,1984,27(1): 31-40.
[19] 王云鹏,韩学山,孙东磊,等. 基于交直流关联最小雅可比矩阵结构的潮流算法[J]. 电力系统自动化,2015,39(7): 1-6.WANG Yunpeng,HAN Xueshan,SUN Donglei,et al. A power flow algorithm based on minimum Jacobin matrix for AC/DC hybrid systems[J]. Automation of Electric Power Systems,2015,39(7): 1-6(in Chinese).
[20] 王艳玲,韩学山,周晓峰. 含分布式电源的输配电系统联合扩展潮流计算[J]. 电力系统保护与控制,2011,39(21): 34-39.WANG Yanling,HAN Xueshan,ZHOU Xiaofeng. Transmissiondistribution joint expanded power flow calculation with distributed generators[J]. Power System Protection and Control,39(21): 34-39(in Chinese).
[21] 刘明松,张伯明,姚良忠,等. 基于PMU和改进戴维南等值模型的电压稳定在线监视[J]. 电力系统自动化,2009,33(10): 6-10.LIU Mingsong,ZHANG Boming,YAO Liangzhong,et al.On-line voltage stability monitoring based on pmu and improved thevenin equivalent model[J]. Automation of Electric Power Systems,2009,33(10):6-10(in Chinese).
[22] 李来福,柳进,于继来,等. 节点戴维南等值参数在线跟踪简捷算法[J]. 中国电机工程学报,2006,26(10):40-44.LI Laifu,LIU Jin,YU Jilai,et al. A simple and direct method of on-line tracking thevenin equivalent parameters of load node[J]. Proceeding of the CSEE,2006,26(10):40-44(in Chinese).
[23] 李卫星,牟晓明,李志民. 电力系统戴维南等值参数的解析与思考[J]. 中国电机工程学报,2012,32(S1): 28-34.LI Weixing,MOU Xiaoming,LI Zhimin. Analysis and thoughts on the thevenin equivalent parameters for power systems[J]. Proceeding of the CSEE,2012,32(S1): 28-34(in Chinese).
[24] VU K,BEGOVIC M,NOVOSEL D,et al. Use of local measurements to estimate voltage-stability margin[J]. IEEE Trans on Power Systems,1999,14(3): 1029-1034.
[25] 谭涛亮,张尧. 计及直流控制方式转换和换流变变比调整的交直流潮流算法研究[J]. 电力系统保护与控制,2011,39(1): 40-45.TAN Taoliang,ZHANG Yao. Study on AC/DC power flow algorithm considering the switching of DC control mode and converter transformer ratio[J]. Power System Protection and Control,2011,39(1): 40-45(in Chinese).

