永磁同步电机伺服系统控制最优化方法

马立新，徐镇乾，范洪成，李光耀

(1.上海理工大学光电信息与计算机工程学院，上海 200093;2.上海机电系统节能工程技术研究中心有限公司，上海 200036)

永磁同步电机(PMSM)具有体积小、结构简单、高转矩惯性比、良好的调速特性及高可靠性等特点，广泛应用于交流调速系统中［1］。它是一个多变量、内部强耦合的高阶非线性系统，运行过程中很多参数会发生变化，PI控制器的控制与电机参数密切相关，因此合理优化PI控制器参数，是电机控制系统研究的关键［3］。

本文研究了粒子群算法(PSO)在永磁同步电机伺服控制系统PI参数寻优中的应用。采用二进制编码方案，设计出适应度函数，调用粒子群算法优化工具箱对PI参数进行整定，目标函数为误差绝对值时间积分型，在Matlab软件中对该系统进行仿真研究，验证了该方法能使控制系统具有更好的动静态性能。

1 永磁同步电机的矢量控制

1.1 坐标变换

永磁同步电机是一个复杂的非线性系统，直接计算电机的磁通、电压、运动和转矩方程是困难的。利用坐标变换，可实现电机模型从三相静止坐标系到两相旋转坐标系之间的变换，简化了方程及空间矢量的计算求解，有利于对电机的控制，坐标变换如式(1)所示［6］。

Clarke变换:即三相静止坐标系(ABC坐标系)和两相静止坐标系(αβ坐标系)3/2变换为

Park变换:即两相静止坐标系(αβ坐标系)和两相旋转坐标系(dq坐标系)的αβ/dq变换为

其中，θr表示d轴与a轴之间的夹角。

上述变换同样适用于电压矢量和磁链矢量［7］。

1.2 永磁同步电机数学模型

永磁同步电机一般采用dq坐标数学模型，该模型不但可用于永磁同步电机稳态运行性能的分析，也能够用于电机瞬态性能的分析。永磁同步电机的转子是由永磁体构成的，磁通一般不会发生变化，故常采用转子磁场的定向控制方法［8］，d、q坐标下永磁同步电机磁链方程为

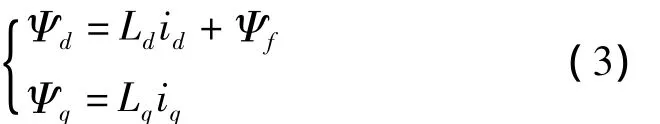
其中，id、iq表示直、交轴电流分量;Ld和Lq表示直、交轴电感;Ψf表示永磁体产生磁链。

d、q坐标系下永磁同步电机电压方程为

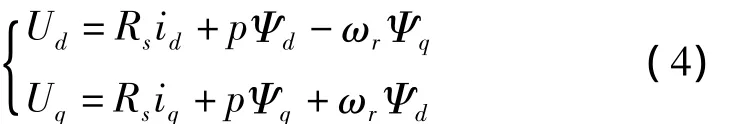
其中，Rs表示电枢绕组电阻;Ψd、Ψq分别表示 d、q轴磁链;P表示微分算子;ωr表示转子角速度。

d、q坐标系下永磁同步电机电磁转矩方程为

其中，Pn表示极对数。

1.3 永磁同步电机PI控制方法

永磁同步电机一般采用PI控制方法，控制结构如图1所示。

图1 传统PI控制方式

PI控制方法的关键就是要找到合适的Kp和Ki，由于伺服控制系统的复杂性，系统中参量的变化使Kp和Ki两个参数具有时变性，应用传统的PI控制方法难以获得最优值［9］。本文采用粒子群算法寻找最合适的Kp、Ki参数，永磁同步电机双闭环伺服控制系统，外环采用转速负反馈闭环控制，通过粒子群算法对PI控制器Kp、Ki参数进化寻优，粒子群算法的优化PI控制结构如图2所示。

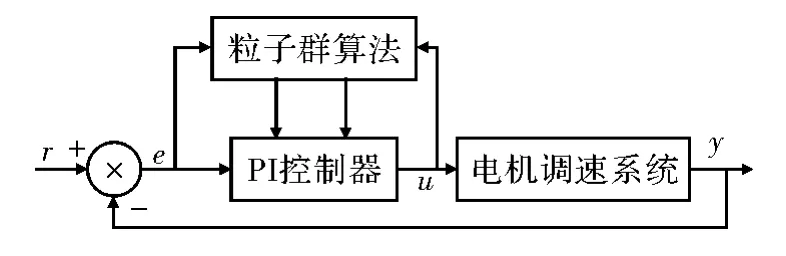
图2 粒子群算法优化的PI控制方式

2 粒子群算法的系统PI参数优化

2.1 粒子群算法

粒子群算法是由心理学家Kennedy和Eberhart在1995年共同提出的一种新的模拟鸟类群体行为的智能优化算法［2］，该算法从一群随机粒子出发，利用迭代方法，使每个粒子根据个体极值Pij和全局极值Gij不断作出调整，搜索到符合要求的值［5］。

带惯性权重的粒子速度和位置更新公式如下:

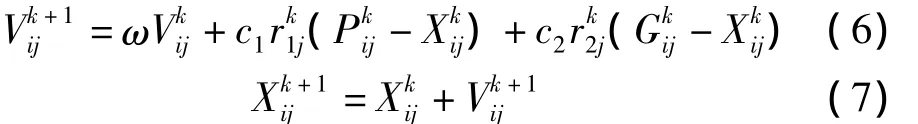
式中，c1和 c2表示学习因子;r1j、r2j表示(0，1)间的两个相互独立的随机数;i表示粒子的序数，j表示该粒子的维数，k表示迭代次数。

2.2 系统PI参数优化设计

(1)粒子的编码方案。由于PI控制器设计实质是一个多维函数的优化问题，对于PI参数Kp和Ki寻优中的粒子可直接采用实数编码Kp和Ki，两个控制参数Kp和Ki组成一个粒子。

(2)粒子群规模。根据相关研究，粒子群的规模设置为20。

(3)初始粒子群形成。采用传统方法得到的Kp和Ki作为初始值，并以该数值为中心向外围扩展，通过随机方式产生初始粒子群。

(4)个体适应度函数计算。适应度函数是粒子群优化算法与控制系统之间的桥梁，适应度函数值代表粒子的质量，即解的精确度。通常永磁同步电机控制系统PI参数寻优时常用阶跃信号作为测试信号，为了提高系统动静态稳定性，目标函数常把误差绝对值的时间积分看作参数的输出［4］，最小目标函数如式(8)所示。

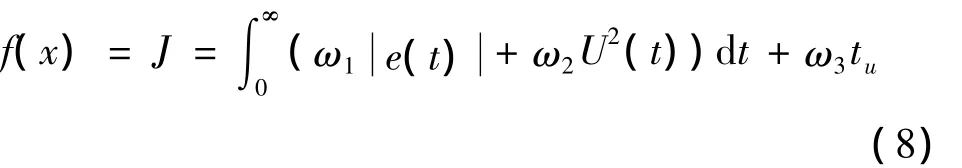
为了抑制超调的出现，采用惩罚功能，即加入超调惩罚因子 ω4(ω4≫ω1)，修正后的最小目标函数如式(9)所示。

其中，e(t)表示系统误差;u(t)表示控制器输出;ω1、ω2、ω3表示权值系数;tu表示上升时间。该类目标函数具有良好的动态寻优性能，但比较繁琐，利用控制器输出u(t)可以避免控制量过大，由于永磁同步电机伺服系统PI控制器均有限幅，因此设置ω2=0;上升时间tu的参数性能误差的绝对值积分较大，为了执行简单，设置ω3=0。

式中，C0为一正常数。

2.3 系统PI参数优化流程

(1)种群初始化。初始化设定种群规模、维数、学习因子、惯性权值、搜索空间、最大迭代次数以及求解精度等参数，获得初始种群。

(2)根据适应度函数计算每个粒子的适应度值。各粒子初始适应度值设定为其个体最优解Pbest，对应的最优位置设置为x0i，对于种群中具有最优适应度的粒子，其适应度值取为全局最优解Gbest，该粒子的位置为最优位置。

(3)将每个粒子当前位置与历史最好位置Pbest和全局最优解Gbest分别做比较，如果优于它们，就替代它们设置。

(4)根据式(9)和(10)计算速度与位置的最新值，若优于之前最优值则替代最优值。

(5)如果更新的粒子结果满足条件或者是迭代次数达到预定的迭代次数，则停止更新，同时输出最优解。否则返回第(4)步更新粒子速度和位置信息。

综上所述可知，系统 PI参数优化流程如图3所示。

图3 系统PI参数优化流程图

3 仿真实验结果研究

3.1 永磁同步电机的参数设置

为验证利用粒子群算法优化的PI控制器的性能，

根据上述f(x)的函数关系式可看出，由f(x)＞0粒子群算法优化f(x)越小越好，因此由f(x)变化到适应度函数F(x)的公式如式(13)所示采用永磁同步电机为研究对象，电机的参数如表1所示。

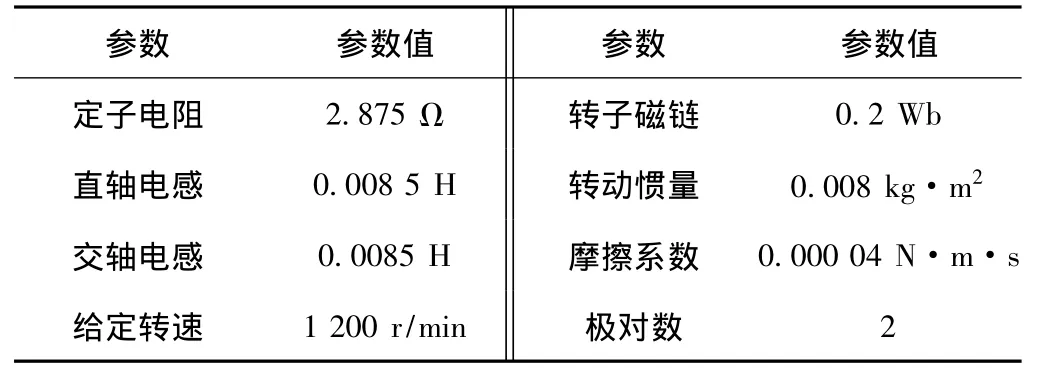
表1 永磁同步电机参数

3.2 PI参数的优化实现

在Matlab R2013b平台进行试验，在Matlab环境下建立的PI参数优化仿真模型如图4所示。

图4 PI参数优化仿真框图

根据试验经验，设置粒子为20，Kp和Ki的取值范围分别为［0，20］和［0，2］，迭代次数设置为100。根据传统方法获取PI控制参数初始值Kp=5、Ki=0.2，经过100次迭代以后观察实验结果。

3.3 仿真实验结果对比

在Simulink中搭建永磁同步电机伺服控制系统的仿真模型，进行如下仿真试验:电机启动时，初始负载转矩为0.3 N·m，启动转速为1 200 r/min，在0.3 s时，将负载加至4 N·m。得到的永磁同步电机伺服控制系统转速波形、转矩对比和三相电流波形分别如图5～图7所示。

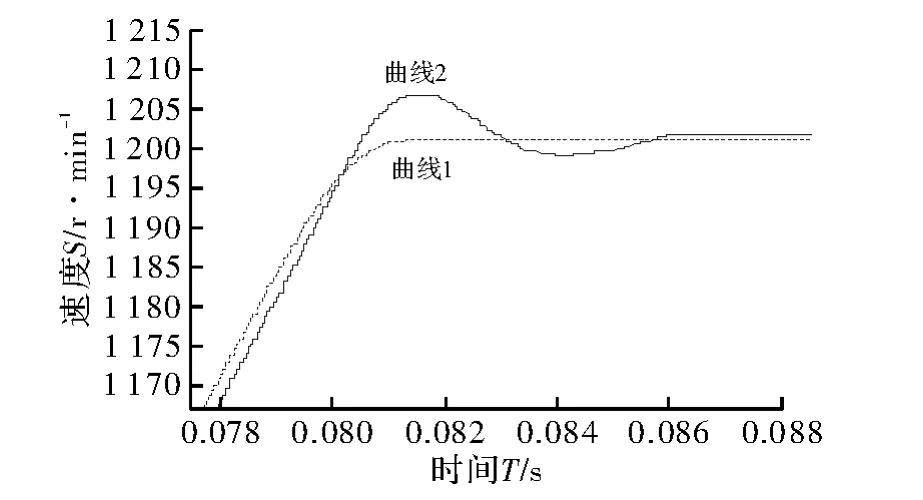
图5 转速响应曲线

图6 转矩响应曲线

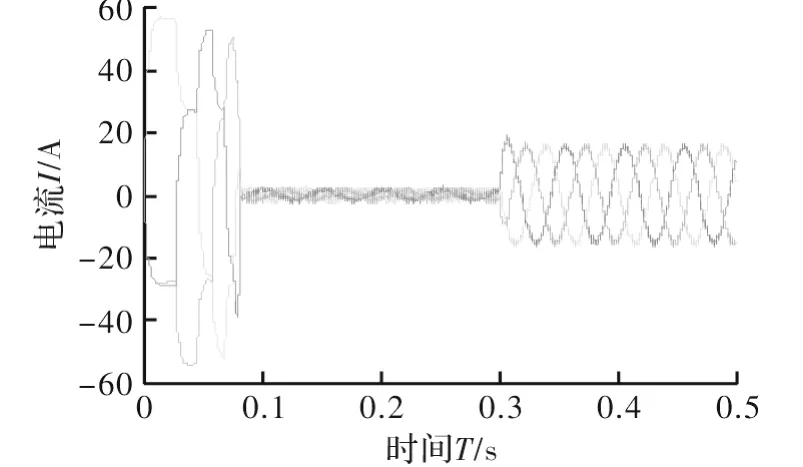
图7 A、B、C三相电流波形

图5中，曲线1和曲线2分别表示装有粒子群算法PI控制器时和传统PI控制器时的速度响应曲线;图6中，曲线3和曲线4分别表示装有粒子群算法PI控制器时和传统PI控制器时的转矩响应曲线;图7表示A、B、C三相电流输出波形。由图中曲线可以看出利用粒子群算法优化的伺服控制系统迅速到达稳定值，超调量极小，到达稳定状态的时间比传统方法短得多。在0.3 s突然将负载转矩由0.3 N·m增加到4 N·m时，利用粒子群算法优化的系统迅速到达稳定转矩值，并且A相电流无抖动，跟随性好。综合上图对比结果说明，通过粒子群算法优化的PI控制器参数，使永磁同步电机伺服控制系统的性能得到明显改善，使系统得到了最优控制。

4 结束语

针对永磁同步电机伺服控制系统PI控制器参数优化问题，提出一种粒子群算法的PI参数优化方法。通过实验对比，粒子群算法对系统PI参数进行在线优化时，提高了系统的运行效率和控制精度，改善了系统的控制性能。与传统PI参数算法相比，本方法更具优越性，更好的提高了系统的动静态性能。

［1］洪乃刚.电力电子、电机控制系统的建模和仿真［M］.北京:机械工业出版社，2010.

［2］潘峰，李位星，高琪，等.粒子群优化算法与多目标优化［M］.北京:北京理工大学出版社，2013.

［3］鲍建成.永磁同步电机PID参数优化研究［J］.计算机仿真，2012，29(4):247 －250.

［4］李明.详解Matlab在最优化计算中的应用［M］.北京:电子工业出版社，2011.

［5］纪震，廖惠连，吴青华，等.粒子群算法及应用［M］.北京:科学出版社，2009.

［6］肖卫文，熊芝耀，李世春，等.基于变参数PI的永磁同步电机矢量控制系统［J］.电力电子技术，2009(4):32－33.

［7］陈伯时.电力拖动自动控制系统－运动控制系统［M］.北京:机械工业出版社，2010.

［8］Liu Huixian，Li Shihua.Speed control for pmsm servo system using predictive functional control and extended state observer［J］.IEEE Transactions on Industrial Electronics，2012，59(2):1171－1183.

［9］Wu Yangyang.Global dynamic sliding mode control of PMSM speed servo systems base on extended state observer［C］.Kunming China:Control Conference(CCC)，2013:4432－4437.