基于差分时间平滑的多径信号DOA估计

彭金龙，陈建春，郭亚萍

(西安电子科技大学电子工程学院，陕西西安 710071)

基于差分时间平滑的多径信号DOA估计

彭金龙，陈建春，郭亚萍

(西安电子科技大学电子工程学院，陕西西安 710071)

针对移动通信环境中，多径信号与独立信号共存的混合信号模型DOA估计问题，依据差分方法与时间平滑原理，提出一种改进的DOA算法。该算法增加了可分辨信源个数，同时提高了相干信源DOA估计的性能，仿真实验证明，该算法在混合信号模型下解相干性能优于传统空间平滑法。

时间平滑;差分;多径信号;移动通信

在现代移动通信系统中，用户方位对某些应用具有重要作用，例如基于用户方位的智能天线可提高通信系统频率和时间复用率，从而满足大容量与高质量的信号传输。移动通信系统中，用户经常处于多径信号环境中，例如同一移动用户的信号经过建筑物反射形成多径传输。由于多径信号来自同一信号源，当多径信号的传播时延差较小时，通常认为这些多径信号是相干的，从而导致传统基于特征子空间的DOA估计失败［1］。

对于相干信源，为了实现DOA估计，常见的一种处理方式是首先采用空间平滑算法解相干［1－3］，然后进行DOA估计。但在实际移动通信环境中，同一基站范围内存在多个用户通话，空间平滑算法由于阵列孔径的损失，降低了空间谱分辨率可检测的信号数目，并且在独立信号与相干信号共存环境中性能恶化。文献［1，3］分析表明:前向、前后向空间平滑算法分别最多只能估计M/2和2M/3个多径信号DOA(M为阵元数)，而实际中多径数目通常远大于此。

时间平滑算法［4－7］利用移动通信信号的衰落特性，在不同的相干时间段内取多个数据块，通过对数据块的协方差矩阵重新整合，使得到的新协方差矩阵达到满秩。时间平滑算法没有阵列孔径损失，但是对于独立信源与相干信源的混合信号模型，无法有效区分，同时导致解相干的信源数降低。基于等距线阵的平滑差分方法［8－9］，首先利用传统的基于特征空间的波达方向估计方法实现独立信号的空间谱估计，再利用空间平滑差分方法实现相关信号的空间谱估计。本文将文献［8～9］的差分思想应用到时间平滑中，提出一种基于差分方法的时间平滑的DOA算法。该方法可以进一步增大可估计信源数目，同时估计性能相对于传统空间平滑算法有明显改善，计算量较小。

1 多径混合信号模型

对于一组多径信号，在时刻的采样数据为Sm(t)，以其中一个信号数据s(t)为参考，根据多径信号的衰落因子，可建立一组多径信号的数据模型

其中，C为多径信号对应衰落因子组成的P×1维矢量(假设P条多径信号)

其中，cm(t)= αm(t)e－jφm(t)。

推广到多个多径信号组，同时包含独立信源，建立独立信号与多径并存的阵列接收数据模型，假设N个窄带远场信号入射到M元阵列。入射信号中独立信源数为Nu，多径信号数为Nc，其中N=Nu+Nc。其中多径信号分成K组相互独立的相干信源，每一组多径信源相干信源数为N，N=∑KN。阵列输出噪声为高kck=1k斯白噪声，且阵元间噪声相互独立，其均值与功率分别为0、σ2N，阵列在t时刻接收数据为

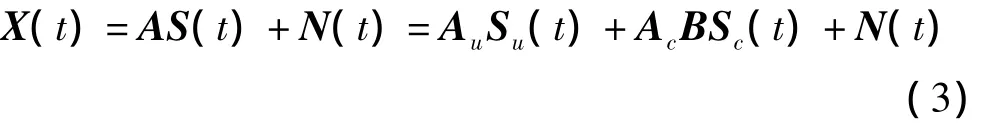
其中，A为M×N维阵列流型矩阵;S(t)为N维入射信号源;N(t)为M×1维阵元输出高斯白噪声;Au为独立信号对应的M×Nu维阵列流型矩阵;Ac为所有多径信源对应的M×Nc维阵列流型矩阵;Su(t)为独立信号数据组成的Nu×1维向量;Sc(t)为K组相互独立的相干信源组中K个相互独立的信源数据组成的K×1维向量;B为多径信号的衰落因子组成Nc×K维块对角矩阵。数学模型为

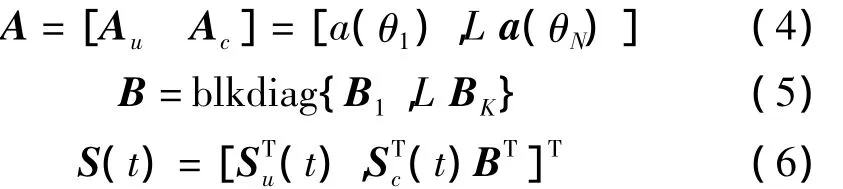
2 基于差分的时间平滑解相干

在移动通信环境中，对于移动的终端，通常用相干时间tcoh=c(vfc)表示时间选择性信道衰落变化的快慢。其中，c、v、fc表示电磁波速度、终端移动速度和载波频率。多径信号与直射信号变化相对较慢，但由于信号波长短，复衰落向量C变化较快，尤其是相位。利用时间平滑算法可将接收数据协方差矩阵恢复为满秩。假设接收数据快拍数为L，将所有快拍数据分成W(W＞P)个数据块，每个数据块的数据长度为D=L/W。对于同一传播路径，当每个数据块的采样时间大于信道相干时间tcoh时，这些数据块多径衰落不相关［7］。

对于所有传播路径及阵列接收数据第j个数据块，对阵列接收数据按列分块，可表示为

式(8)中X为阵列接收数据，则数据块对应的协方差矩阵为

对W个数据块的协方差矩阵求平均得到时域平滑的协方差矩阵为

基于时域平滑的解相干算法不存在阵列孔径损失，对阵列结构没有要求，但为了解相干，数据块需要足够的观察时间使得相邻数据块采样起始时间间隔tcoh，使得不同采样数据块的衰减因子C不相关［5］。采用数据块时域平滑算法，只要满足数据块个数W＞P，可以得到满秩的协方差矩阵 Rts［7］。

针对多径混合信号，为提高算法性能，同时增大可估计信号数目，本文提出一种差分时间平滑算法。对于Toeplitz矩阵Rt满足:JRTtJ=Rt，其中，J 为反对角单位矩阵。式(7)中Ru为对角阵，满足Toeplitz特性，有JRTuJ=Ru，但Rc不满足Toeplitz特性。所以可以构造多径相干信号的数据协方差矩阵为

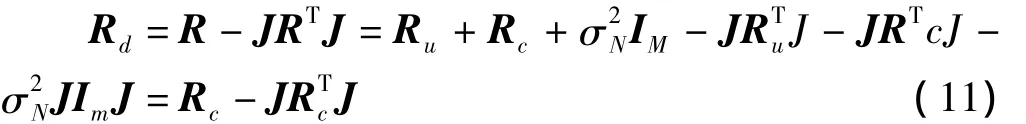
求得协方差矩阵不含独立信源分量，与时间平滑算法结合，可以获得满秩的协方差矩阵，利用传统子空间算法例如MUSIC算法可对多径相干信源进行有效DOA估计。

根据以上讨论，基于差分方法的时间平滑算法可归纳如下:

(1)由阵列接收数据X及快拍数L，计算阵列协方差矩阵估计值

(3)根据式(8)与式(9)求出数据块的协方差矩阵R^(j)。

(4)利用式(11)求得每个数据块只包含多径信源协方差矩阵分量的差分矩阵。

3 仿真分析

仿真1 均匀线阵阵元数M=8，阵元间距等于半波长。两个多径相干信号组成相干信源组，多径信号波达方向与衰落系数分别为{0°，10°}，{1，exp(i2π(2rand(1)－1))}。一个独立信源入射到天线阵列上，波达方向为30°，信噪比SNR=10 dB。分别用空间平滑，差分时间平滑算法进行DOA估计，时间平滑数据块数。对多径信号的估计结果如图1所示。空间平滑算法在混合信号模型由于天线孔径损失中性能恶化，可以看出差分方法时间平滑DOA算法有效去除了独立信源信息，同时估计多径信号性能良好，增大了阵列天线可估计相干信源数目。

仿真2 阵列与仿真1相同，在4个多径信号入射到天线阵列上，波达方向分别为{－20°，0°，20°，30°}，信噪比为SNR=10 dB。分别用空间平滑，差分时间平滑算法进行DOA估计，时间平滑数据块数W=10。对多径信号的估计结果如图2所示。根据仿真结果，可说明该算法对全相干信源模型依然有效，由于差分方法损失了部分多径相干信号的信息，相对于空间平滑算法，该算法性能有一定损失。

图1 估计混合信号

图2 估计相干信号

仿真3 阵列同仿真1，为简化信号模型，如仿真1混合信号模型，信号入射方向与衰落系数同仿真1，结合RootMUSIC进行DOA估计，并研究估计多径信号的性能，研究估计均方误差RMSE与信噪比SNR关系。独立进行200次蒙特卡洛试验的仿真结果，如图3所示。

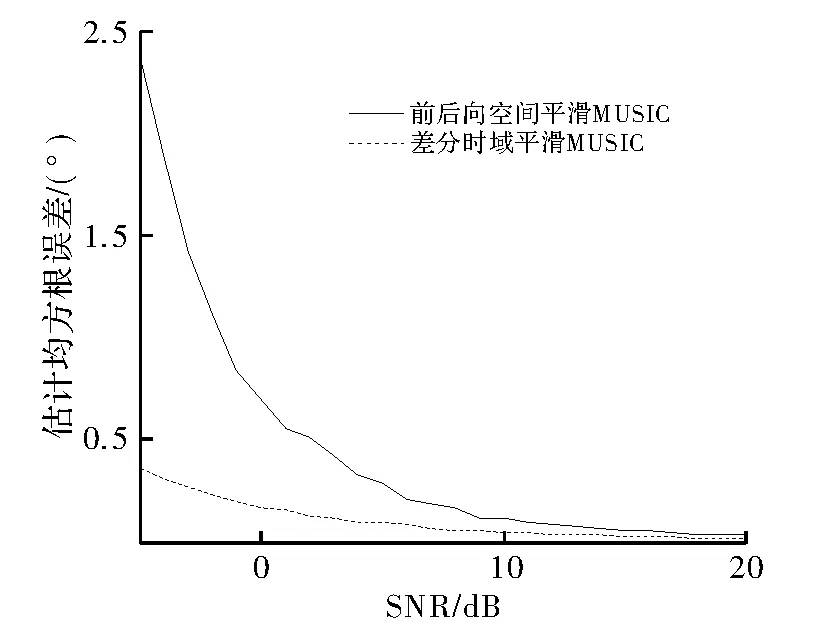
图3 估计均方误差

仿真4 阵列、混合信号模型、信号入射方向与衰落系数均与仿真1相同，结合RootMUSIC进行DOA估计，并研究估计多径信号的性能，研究估计多径信号成功率与信噪比的关系。仿真结果如图4所示。

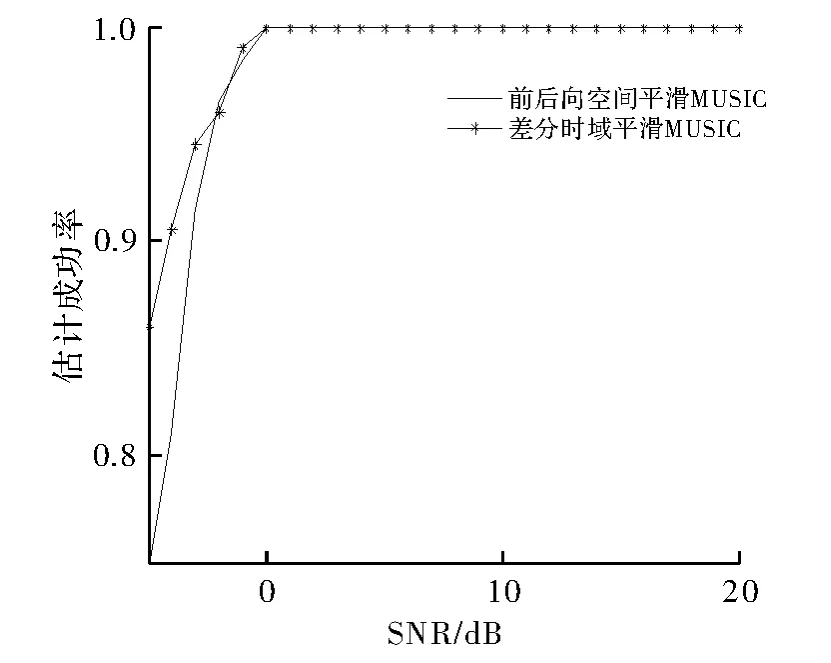
图4 估计成功概率

4 结束语

本文介绍了一种移动通信多径信号的DOA算法，基于多径信号的衰落特性，利用时间平滑与差分方法，对多径信号有效解相干。该算法采用时域平滑，不存在孔径损失，使可估计信源数增加，分离了独立信源的影响，提高相干信源DOA估计的性能。理论与仿真分析表明，该算法性能在混合信号模型中优于经典空间平滑算法，对入射信号全部为相干信源的解相干能力有待改进。

［1］Shan T J，Wax M，Kailath T.On spatial smoothing for direction of arrival estimation of coherent signals［J］.IEEE Transactions on ASSP，1985，33(4):806 －811.

［2］Piltai S U，Kwon B H.Forward backward spatial smoothing techniques for the coherent signal identification［J］.IEEE Transactions on Acoustics，Speech，and Signal Processing，1989，37(1):8 －15.

［3］WiIIiams R T，Prasad S，MahaIanabis A K，et aI.An improved spatial smoothing technigue for bearing estimation in a multipath environment［J］.IEEE Transactions on ASSP，1988，36(4):425 －432.

［4］van Rheeden D R，Gupta S C.A temporal smoothing approach to direction of arrival estimation of coherent signals in fading channels［C］.Newyork:Wireless Communications and Networking Conference，IEEE，1999:286 －290.

［5］Gu Z H，Gunawan E.A performance analysis of multipath direction finding with temporal smoothing［J］.IEEE Transactions on Signal Processing Letters，2003，10(7):200 －203.

［6］何子述，韩春林，唐斌.一种有效的多径信号DOA估计算法［J］.电子学报，2003，3l(1):139 －141.

［7］张森，陈永革，郭艺夺，等.基于时域数据块平滑的多径信号DOA估计算法［J］.雷达科学与技术，2010，8(5):429 －421.

［8］Zhang Yufeng，Ye Zhongfu.Efficient method of DOA estimation for uncorrelated and coherent signals［J］.IEEE Antennas and Wireless Propagation Letters，2008(7):799 －802.

［9］Guo Yiduo，Zhang Yongshun，Tong Ningning.A new DOA estimation method for uncorrelated and coherent sources under nonstationary noise fields［C］.Changsha:IEEE 8th International Conference on Application Specific Integrated Circuit，2009:987－990.

［10］王永良，陈辉，彭应宁，等.空间谱估计理论与算法［M］.2版.北京:清华大学出版社，2005.

DOA Estimation of Multipath Signals Based on Differential Temporal Smoothing

PENG Jinlong，CHEN Jianchun，GUO Yaping
(School of Electronic Engineering，Xidian University，Xi'an 710071，China)

An improved DOA algorithm is proposed for the mixed signal model where independent signals and multipath signals coexist in the mobile communication environment based on the differential method and temporal smoothing principle.The algorithm increases the number of signal sources resolved and promotes the DOA estimation performance of coherent signals.Simulation results show that the algorithm has better performance in the mixed signal model than the traditional spatial smoothing method.

temporal smoothing;differential;multipath signals;mobile communication

TN929.5

A

1007－7820(2015)06－162－04

2014-10-29

彭金龙(1989—)，男，硕士研究生。研究方向:基于差分时间平滑的多径信号DOA估计。E-mail:525545597@qq.com

10.16180/j.cnki.issn1007－7820.2015.06.044