推拉效应对心血管系统影响的建模仿真研究
刘 洋,冯 娜,张 曦,常小红,卢虹冰
推拉效应对心血管系统影响的建模仿真研究
刘 洋,冯 娜,张 曦,常小红,卢虹冰
目的:建立可仿真推拉效应引起人体心血管变化的、非线性分布式人体心血管系统模型,并通过与真实实验数据对比,验证模型的有效性。方法:在分析推拉效应对心血管系统影响的基础上,对模型进行设计,并利用Pascal语言,建立一个将心脏、血管系统和反馈机制相结合的闭环心血管系统模型。结果:建立的分布式模型包括左、右心室和心房4腔室,大中动、静脉血管各22段,中小动、静脉等外周血管12段,并包含颈动脉压力调节和静脉塌陷模型。仿真结果与报道的人体旋转床和离心机实验数据相近。结论:该模型可以有效地模拟飞行员做推拉动作时心血管系统的响应,为推拉效应的研究提出了一个经济、实用的方法。
推拉效应;心血管系统;建模;仿真
0 引言
持续正加速度(+Gz)致意识丧失的机理及防护是航空医学的重要问题。然而,与单纯的+Gz相比,预先暴露于<1 Gz、0 Gz或-Gz,再立即转为+Gz作用时,更容易发生意识丧失,这种现象称为“推拉效应”(push-pull effect,PPE)[1],产生PPE的动作称为“推拉动作”(push-pull maneuver,PPM)。由于PPE可引起飞行事故,严重危及飞行安全,因此许多国家都针对PPE展开大量研究,是目前航空医学加速度生理领域的研究热点之一。
目前,对PPE的研究主要有真实的飞行试验和地面试验2种。由于飞行试验昂贵,而且还受到机会、样本数量、测量方法、试验环境等多种因素限制,所以不能大量采用。地面试验主要采用下体正压[2]、旋转床[3-4]和离心机[5-6]等方法。虽然地面模拟产生的生理学变化与PPM过程中的观察结果相似,但在模拟PPM加速度曲线的过程中仍存在局限性。例如:下体正压的压力与PPM动作中push时相的G值幅度之间的关系不确定;旋转床的G值范围限定在-1~1 Gz,而且时相间的转换速率不确定;离心机的基线值根据不同的系统配置在1.4~1.8 Gz间变化,与正常飞行的1 Gz存在一定的差异[7]。所以,与上述试验方法相比,数学模型是一种低成本、综合的实验方法。作为实验研究的补充,数学模型可以有效地模拟各种影响因素对+Gz耐力的影响[8],特别对PPE的研究更有特殊意义。
本文根据PPE的特点,建立了一个可以仿真PPM的非线性、分布式心血管系统模型,模型包含人体各主要器官、生理反馈补偿以及快速血压变化引起的静脉塌陷等模块,并通过与真实试验数据对比,验证模型的有效性。
1 模型的设计
PPM易引起人体各部分血管血压的快速、大幅变化,故建立的心血管系统模型应具有如下特性:
(1)为模拟PPM引起的血液分布变化,模型应为一个分布式的多元模型,其中包括心脏、脑部、胸部、腹部和肢体各主要部分。
(2)为模拟PPE作用下颈动脉血压变化引起的生理反馈,补偿机制应包含心率(heart rate,HR)反馈控制等生理调节与控制机制。
(3)由于在PPM过程中,血压随G负荷快速变化而大幅度波动,血液在上下肢大量移动,静脉血管易发生塌陷,故应包含静脉塌陷模型。
在分析PPE特点的基础上,建立了一个将心脏、血管系统和反射机制相结合的闭环心血管系统模型。该模型包括左、右心室和心房4腔室,大中动、静脉血管各22段,中小动、静脉等外周血管12段。心血管系统各组分的生理参数值的初始值均来自人体解剖数据和文献[9],无相应数据的参数则通过参数估计及曲线拟合推出。建立的非线性、分布式心血管系统模型框图如图1所示。
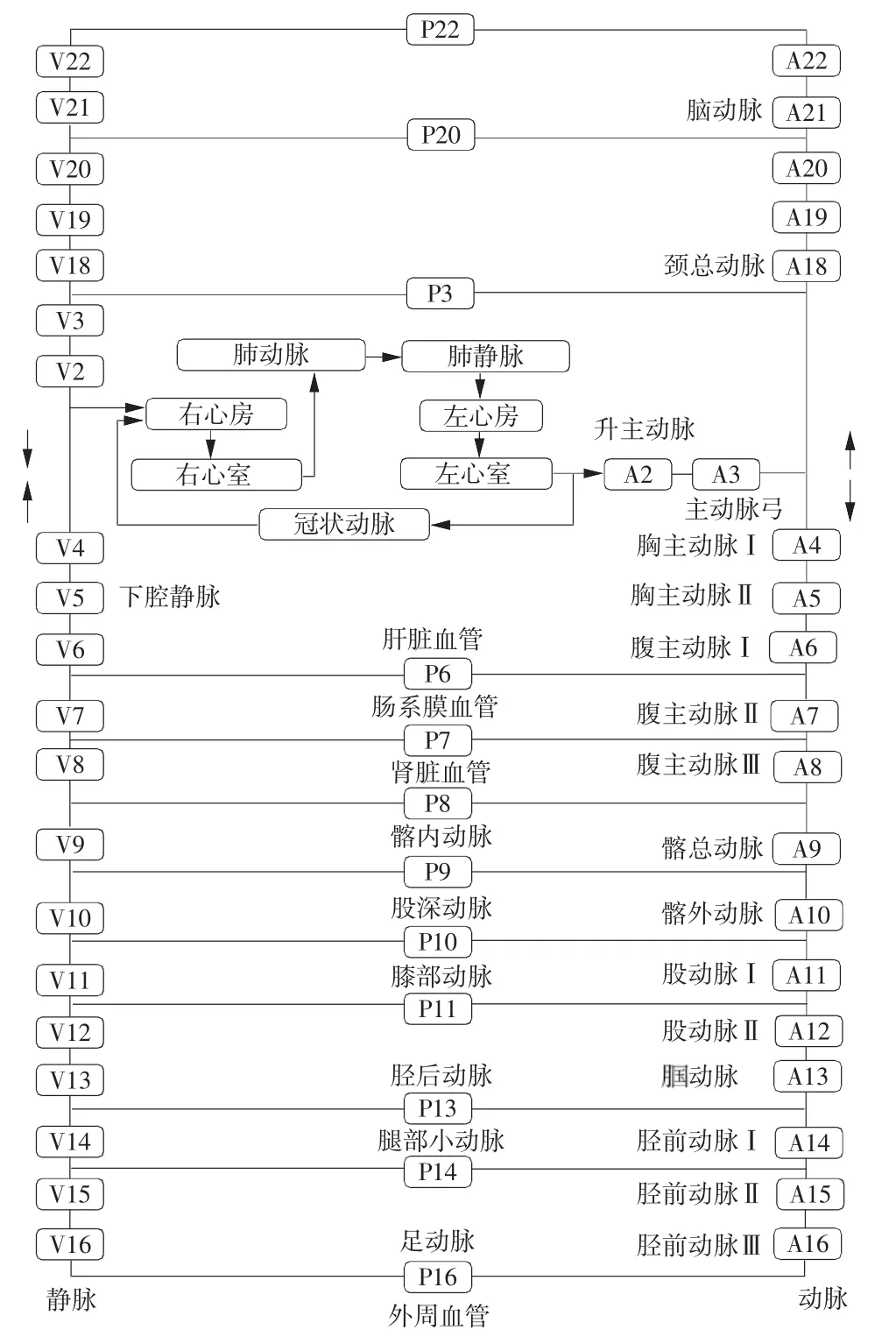
图1 非线性心血管系统模型框图
2 分布式心血管系统模型的建立
本研究所建立的模型,包括4腔室的心脏模型、血管模型、肺循环模型、颈动脉压力调节模型和静脉塌陷模型。
2.1 心脏模型
心脏是人体最重要的器官,是整个心血管系统的核心部分。人体的心脏分为左心和右心2个部分,分别驱动体循环和肺循环。由于左右心在结构和功能上是相似的,故在模型中,采用了结构相同但参数不同的2个等效网络。在本研究中,心室和心房均采用Suga和Sagawa提出的时变弹性模型[10]。以左心室为例,心室压力-容积随时间的变化关系可以用一个时变弹性系数Elv(t)来描述。心动周期中某时刻,左心室压力plv(t)可通过如下公式获得:
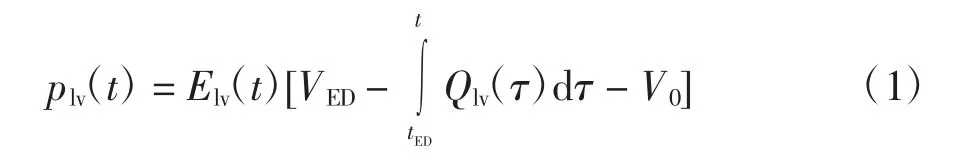
式中:Qlv(τ)为左心室血流;VED为心室舒张末期容积;tED为舒张末期对应时刻;V0为心室压力-容积曲线在收缩末期其最大斜率与容积轴的截距。
2.2 血管模型
模型中将人体血管系统分为有限个小段进行处理。为简化计算过程,假设:血液为不可压缩的牛顿液体;血管为薄壁直血管;除主动脉上升支和主动脉弓外,其余部位血管中的流动均为轴对称的层流,其流速呈抛物线分布;血压只考虑其轴向变化;忽略血管壁的运动,则由Navier-Strokes方程[11]得到各段血管压力p、流量Q的关系如下:
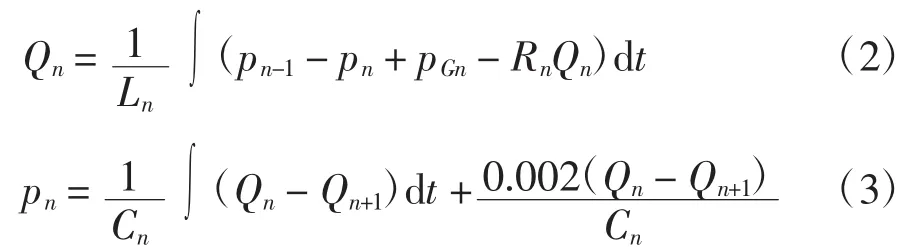
式中:Rn、Ln及Cn分别为第n段血管的等效流阻、等效流感及血管顺应性,各元件的值可由求出,其中,ρ为血流密度,rn为血管半径,ln为血管长度,hn为管壁厚度,u是黏滞系数,E是管壁的弹性模量,Vn为血管容积;pGn表示由重力引起的血流静力学压强,可通过pGn= ρGzlncos θn获得,其中Gzlncos θn表示整个加速度沿血管长度ln方向的分量。
2.3 肺循环模型
在本研究中,采用集总参数模型来模拟肺循环,采用的等效电路如图2所示。其中,二极管模拟起到单向阀作用的肺动脉瓣膜。
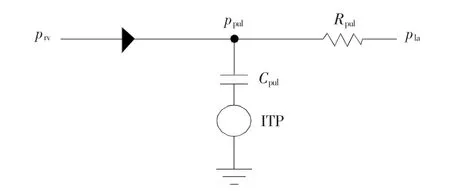
图2 肺循环子模型等效电路
2.4 压力反射调节子模型
压力反射调节是一种负反馈调节机制,其生理意义在于使血压保持稳定。当血压高于压力感受器的阈值,降压反射就将起到调节作用。在推拉效应中,颈动脉压力反射起到了重要的调节作用[12]。为了更好地模拟PPM对心血管系统的响应,基于Ursino[13]提出了颈动脉压力反射模型,建立压力反射调节子模型。
颈动脉窦感受压力牵张,压力牵张的绝对值和其变化快慢转换成电脉冲由传入神经传入位于脑干的神经中枢,再由神经中枢作出适当响应,由交感和迷走传出神经通路将调节信息传输到效应器。在本研究中,共模拟了HR、动脉阻力、心脏收缩性、静脉容积和血管紧张度5个效应器的作用。HR受到交感和迷走神经的调节,而其余4个只受到交感神经影响。其中,动脉阻力、心脏收缩性、静脉容积受交感神经调节,可用如下公式表示:
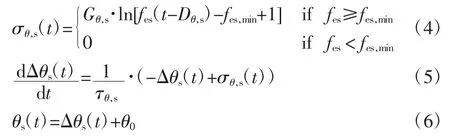
式中:θs代表交感神经调节的不同机制;σθ,s为静态特征方程的输出;τθ,s、Dθ,s为不同调节机制的时间常数和延迟时间;fes是传入交感神经的放电频率;fes,min为fes的最小值;Gθ,s为增益常量,对于外周阻力、心脏收缩性而言Gθ,s为正,而对于静脉容积Gθ,s为负。
HR的调节受到了交感和迷走神经的影响,心动周期T受迷走神经的影响可用如下公式表示:
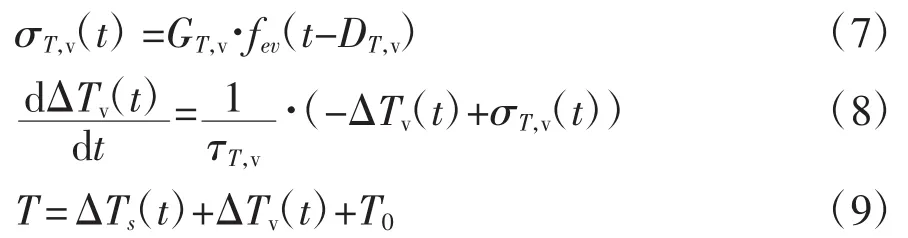
式中:ΔTs可通过式(4)和式(5)获得,式(7)和式(8)中的符号与式(4)和(5)相对应,v为迷走神经。在获得对心动周期T的调节后,HR可由1/T来获得。
在本研究中,血管紧张度的调节,采用Green和Miller提出的模型[14],模型可用如下公式表示:
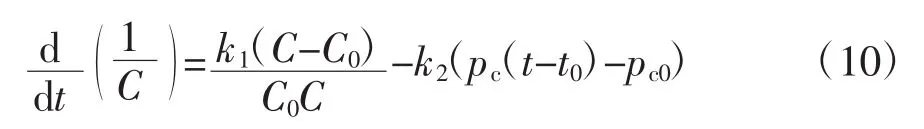
式中:C为血管紧张度;pc为颈动脉压;k1和k2为常数;t0为与HR相关的时间延迟。
2.5 静脉塌陷子模型
在PPM过程中,血压随+Gz负荷快速变化而大幅度波动,虽然大部分动脉可以保持形状不变,但由于静脉的血管壁较薄,且内部压力较低,容易发生塌陷。当静脉的内外压差小于0时发生血管塌陷。在模型中,发生形变的血管的横截面用恒定周长的椭圆来表示[15]。此时,该静脉血管段的压降Δp,可用如下公式表示:
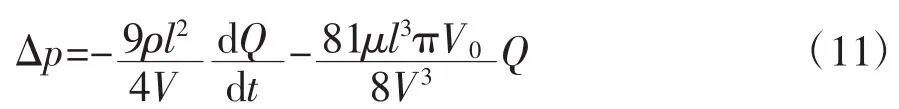
式中:V为血管的容积;V0为血管内外压差为0时的血管容积;Q为流量。
3 模型有效性验证
3.1 计算机仿真方法
模型模拟的虚拟人身高为1.8 m,静息状态下的心率为72次/min,心输出量为5.6 L/min,左心室收缩压为113.5 mmHg(1 mmHg=0.133 3 kPa)。眼部动脉收缩压为86.3 mmHg,心眼距离为37 cm。模型利用Pascal语言开发,计算的时间间隔设定为0.001 s。在每个时间间隔,由左心室开始,逐段血管地计算血压、血流和容积。随着静脉血回流至右心房,肺循环始于右心室。模型在开始运行4~5个心动周期后输出趋于稳定,2.8 GB CPU、1 GB内存的计算机,计算一个心动周期约需时12 ms。
在模型中,各血管段压力梯度的变化可反映重力的影响,+Gz负荷的影响由改变相应局部血管段沿血管方向的重力分量来模拟。为了模拟真实的飞行环境,虚拟人取坐姿,后仰座椅的倾斜角度为13°,大腿和水平的夹角为11°,小腿和水平的夹角为60°。离心机实验已经证明,当眼部血管的动脉压低于50mmHg,外周视觉开始丧失;而当血压在20mmHg时,视觉完全丧失[16]。所以,在模型中,选取眼部血管的动脉压为30 mmHg时为达到+Gz耐力的标准。
图3描述了PPM和正常的超重加速度曲线。在PPM加速度曲线中,包含了5个影响因素,包括初始基线值、push时相的G值变化率、push时相的G值幅度、push时相的持续时间和pull时相的G值变化率。每个影响因素都会引起+Gz耐力的变化。
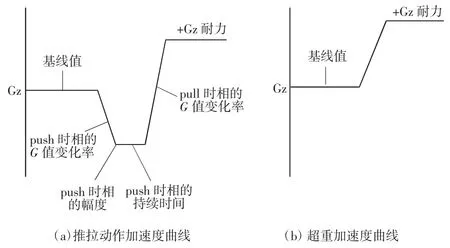
图3 加速度曲线
3.2 仿真内容
为了验证该模型在PPE研究方面的有效性,在相似的实验环境下,将+Gz耐力和其他生理变量的模型输出结果与Goodman[6]和Sheriff[4]的离心机及旋转床的人体实验结果进行比较。Goodman的实验利用多轴离心机,PPM和对照加速度曲线的基线值都为1.4 Gz,G值变化率设定为±2 Gz/s,push时相的G值幅度为-1 Gz,持续时间为5 s,并在push时相施颈动脉外部加压(neck pressure,NP)。Sheriff利用旋转床进行实验研究,被试者从平卧位旋转至-15°头低位倾斜,持续20 s,接着立即旋转至30°头高位倾斜,持续时间为30 s。在实验中,手动转变旋转床角度的时间小于2 s;在模型中,G值变化率(旋转角度的速率)为±2 Gz/s。
3.3 仿真结果
表1给出了在相似条件下仿真结果与Goodman实验结果[6]的比较。比较结果表明,仿真结果与实验结果基本吻合。同时,无论实验结果还是仿真结果都说明了颈动脉外部加压(NP)虽然可以提高+Gz耐力,但是提高的幅度很小。

表1 仿真结果与Goodman实验结果[6]的对比Gz
表2给出了在相似条件下仿真结果与Sheriff实验结果[4]的比较。由表中数据可知,实验结果与仿真结果都表明,在push时相,眼水平动脉压(eye-level arterial pressure,ELAP)增加,HR和心输出量(cardiac output,CO)都降低。而在pull时相,ELAP、HR和CO都向相反方向变化。比较结果表明:除HR的基线值略高于实验数据外,大部分仿真结果与实验结果基本吻合。

表2 仿真结果与Sheriff实验结果[4]的对比
4 讨论
本研究建立了适用于PPE研究的多元非线性人体心血管系统模型。鉴于人体心血管系统的构成及控制机理极为复杂,要想提出一个能全面反映其各种机理的模型几乎是不可能的。但是本研究所建立的模型,由于其模拟结果与实际获得的有限数据基本吻合,表明此模型可用于研究PPM对人体心血管系统的影响。由于模型研究可获得试验中很难或根本不可能得到的数据,故可预测PPE作用下人体循环各部分的血压、血流等变量的数值,因此可在一定程度上代替动物或人体实验,特别是作为人体实验前的预备研究工作,是经济而有效的。在下一步工作中,我们拟将模型仿真与人体实验进一步结合,在实验数据的基础上进一步完善模型,并利用模型进一步指导实验。
[1] Banks R D,Grissett J D,Turnipseed G T,et al.The"push-pull effect"[J].Aviat Space Environ Med,1994,65(8):699-704.
[2] ZHANG W X,ZHAN C L,GENG X C,et al.Decreased+Gz tolerance following lower body positive pressure:simulated push-pull effect[J].Aviat Space Environ Med,2001,72(11):1 045-1 047.
[3] Goodman L S,LeSage S.Impairment of cardiovascular and vasomotor responses during tilt table simulation of"push-pull"maneuvers[J]. Aviat Space Environ Med,2002,73(10):971-979.
[4] Sheriff D D,Nådland I H,Toska K.Hemodynamic consequence of rapid changes in posture in humans[J].J Appl Physiol,2007,103(2):452-458.
[5] Goodman L S,Banks R D,Grissett J D,et al.Heart rate and blood pressure responses to+Gz following varied-duration-Gz[J].Aviat Space Environ Med,2000,71(2):137-141.
[6] Goodman L S,Grosman-Rimon L,Mikuliszyn R.Carotid sinus pressure changes during push-pull maneuvers[J].Aviat Space Environ Med,2006,77(9):921-928.
[7] BanksRD,BrinkleyJW,AllnuttR,et al.Fundamentals of Aerospace Medicine[M].4th ed.Philadelphia:Lippincott Williams&Wil-kins,2008:93-97.
[8] LU H B,ZHANG L F,BAI J,et al.Mathematical modeling of high G protection afforded by various anti-G equipment and techniques[J]. Aviat Space Environ Med,2007,78(2):100-109.
[9] Sheng S,Sarwal S N,Watts K C,et al.Computational simulation of blood flow in human systemic circulation incorporating an external force field[J].Med&Biol Eng&Comput,1995,33(1):8-17.
[10]Suga H,Sagawa K.Instantaneous pressure-volume relationships and their ratio in the excised,supported canine left ventricle[J].Circ Res, 1974,35(1):117-126.
[11]白净.生理系统的仿真建模[M].北京:清华大学出版社,1994:85-115.
[12]LIU Y,ZHANG L F,ZHANG K L,et al.Role of carotid baroreflex and sympathetic responses in pushpull effect:a simulation study[J].Aviat Space Environ Med,2012,83(9):841-849.
[13]Ursino M.Interaction between carotid baroregulation and the pulsating heart:a mathematical model[J].Am J Physiol,1998,275(5 Pt 2):1 733-1 747.
[14]Green J F,Miller N C.A model describing the response of the circulatory system to acceleration stress[J].Ann Biomed Eng,1973,1(4):455-467.
[15]Synder M F,Rideout V C.Computer simulation studies of venous circulation[J].IEEE Trans Biomed Eng,1969,16(4):325-334.
[16]Shubrooks S J,Leverett S D.Effect of the valsalva maneuver on tolerance to+Gz acceleration[J].J Appl Physiol,1973,34(4):460-466.
(收稿:2015-01-05)
Modeling and simulation for cardiovascular effect induced by push-pull effect
LIU Yang1,FENG Na2,ZHANG Xi1,CHANG Xiao-hong1,LU Hong-bing1
(1.School of Biomedical Engineering,the Fourth Military Medical University,Xi'an 710032,China;2.Teaching and Research Section of Physiology,School of Basic Medicine,the Fourth Military Medical University,Xi'an 710032,China)
ObjectiveTo develop a nonlinear and distributed cardiovascular system model,which can simulate the cardiovascular effect induced by push-pull effect(PPE).MethodsThe model was designed based on the analysis of the effect of PPE on cardiovascular system.Programmed with Pascal language,the closed-loop model was combined with heart,vessels and baroreflex regulation.ResultsThe developed model consisted of left and right ventricles and atria,22 segments of arteries and veins,12 segments of peripheral vascular beds,carotid blood pressure regulation,and vein collapse model.The simulation results compared well with reported data from tilt-table and centrifuge experiment. ConclusionThe model can simulate the cardiovascular response to push-pull maneuver and may be an economical and practical method to investigating PPE.[Chinese Medical Equipment Journal,2015,36(4):12-15]
push-pull effect;cardiovascular system;modeling;simulation
R318;TP391.9
A
1003-8868(2015)04-0012-04
10.7687/J.ISSN1003-8868.2015.04.012
军队医学科技青年培育项目(13QNP126)
刘 洋(1981—),男,博士,主要从事生理信号仿真和医学图像处理方面的研究工作,E-mail:yliu@fmmu.edu.cn。
710032西安,第四军医大学生物医学工程学院(刘 洋,张 曦,常小红,卢虹冰),基础部生理学教研室(冯 娜)

