基于混合整数规划的仓库选址研究
杨 彪,周亦鹏 YANG Biao, ZHOU Yi-peng
(北京工商大学 计算机与信息工程学院,北京100048)
(School of Computer and Information Engineering, Beijing Technology and Business University, Beijing 100048, China)
0 引 言
仓库是物流网络上的节点,是物流网络规划的重要对象。仓库选址合理与否对物流供应成本的高低有重要影响。混合整数规划是一种同时包含离散变量和整数的数学规划方法,应用范围很广泛,在物流领域主要应用在运输、物流中心选址等方面。本文将应用混合整数规划方法进行纤维乙醇企业原料仓库的选址,并确定各仓库的吞吐能力,为相关产业的规划提供指导。
1 纤维乙醇产业与原料供应模式概述
燃料乙醇是生物液体燃料中的一种,而纤维乙醇又是目前燃料乙醇中研究和发展的重点。它是利用生物质(如秸秆) 中的纤维素经酶解、发酵等环节来生产乙醇,为与用粮食生产的第一代燃料乙醇相区别,被称作第二代燃料乙醇,相比于第一代燃料乙醇具有不与人争粮的优点[1]。在我国,将燃料乙醇按10%的比例添加在汽油中可以直接在汽车中使用[2]。但由于相关技术问题,目前纤维乙醇产业还处于技术研究和产业化试点示范阶段,生产规模很小,一般只能满足城市内部需求。
纤维乙醇的重要原料是农作物秸秆。秸秆的供应始于田地,结束于乙醇生产厂。这个供应过程包括田间收获、装卸搬运和预处理、储存、运输等环节。主要流程如下:(1) 田间收集秸秆;(2) 田间秸秆的预处理与运输,其中预处理包括压缩、打捆等;(3) 秸秆储存,储存点可以设定在田边、收储站、电厂料场或仓库;(4) 道路运输及装卸[3]。
一般而言,当生产厂规模较小时,企业可以直接从农户手中采购秸秆,或经经纪人或合作社采购秸秆。这种情况下,秸秆的收购范围、收购量都较小,所收购的秸秆或者先在临时收购站集中后运往生产厂,或者直接运往生产厂储存。当生产厂规模较大时,相对单一的秸秆产区难以满足生产厂的需要,其秸秆收购区域往往不只一个,且距离生产厂都比较远,直接运往生产厂势必会大量增加运输成本,这时就需要建设收购站或原料仓库收集和储存秸秆,再按需求供应生产厂。由此可知,当生产规模比较大时,秸秆原料的供应模式是三级供应链模式。三级供应链是最典型最基本的供应链形式,它在管理上存在的问题能很好反映供应网络上问题,在对三级供应链中物流中心进行选址时一般会将物流中心的建设规模作为决策量[4]。其供应模式可以用图1 表示。
由图中可知,有若干个秸秆产区、若干个原料仓库备选地和若干个乙醇生产厂,那么原料仓库选址的目的就是根据秸秆的需求量、产区的供应量、仓库的建设成本、原料的运输成本等数据,建立混合整数规划模型,计算求得原料仓库的位置和规模,使总供应成本最低。
2 利用混合整数规划模型进行原料仓库选址
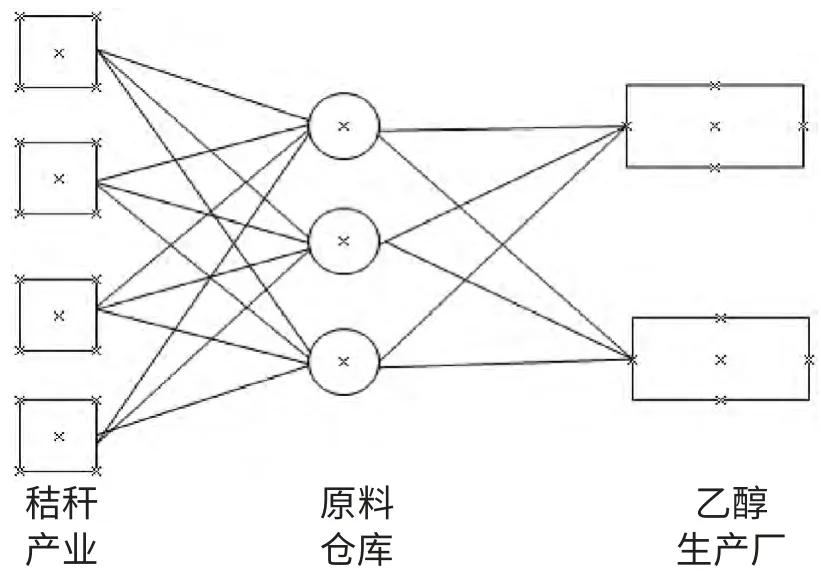
图1 秸秆供应链模型
2.1 数据整理
本文以山东省为例,研究纤维乙醇企业原料仓库的选址问题。通过查询山东省统计局网站,首先获得了山东省2012 年全省平均每天消耗的汽油吨数,进而估算出2012 年全省全年消耗汽油总量。同时还查询到了2012 年山东省各市的民用汽车保有量,计算得到各市民用汽车保有量占全省民用汽车保有量的百分比。并用此百分比分配2012 年山东全省的汽油消耗总量,求得2012 年山东省各市的汽油消耗总量。再按国内现行的乙醇汽油10%的燃料乙醇添加量求得2012 年山东省各市的燃料乙醇需求量。根据国内秸秆与纤维乙醇的平均转化比例6∶1,可求得满足各市乙醇需求量所需的秸秆总量。此外,还获得了2012 年山东省各市的小麦、玉米产量,这是计算2012 年小麦、玉米秸秆供应量的基础。为计算秸秆供应量还需要确定相应的草谷比系数和秸秆的可收集系数。表1 和表2 给出了这两个系数的确定依据。

表1 部分农作物秸秆草谷比系数[5]

表2 部分农作物秸秆可收集系数
农作物的草谷比系数受气候、地域、农作物品种、种植制度、收集方法、测量方法等多种因素的影响。所以文献中所用的草谷比系数有较大的差异,本文采用了几个较权威文献中的草谷比的平均值。而可收集系数采用了学者崔明等人的研究成果,他认为秸秆的可收集系数要根据不同收集方式的权重来确定。利用这两个系数便可以计算出山东省2012 年秸秆的可供应量。其公式如式(1) 所示:

其中,n表示农作物种类数;Qci表示某农作物的产量;ri表示某农作物的草谷比系数;ki表示某农作物的秸秆可收集系数。
2.2 模型建立
秸秆的供应成本主要包括购买成本、运输成本、装卸成本和仓库建设运行引起的成本,不包括储存成本。因为当生产厂产量固定时,秸秆的年需量一般为定值,且必须经过储存来降低水分,所以其购买成本为定值(不考虑市场供需、价格浮动),年储存成本为定值,这两部分成本不能通过优化得到降低。另一方面,由于秸秆的年总运输量(假设生产厂运行稳定后,每年的秸秆消耗量和运输量相等) 为定值,因此每年的秸秆装卸量也为定值,在不考虑运输车辆、装卸工具规格等的情况下,秸秆的装卸成本也为定值,无需优化。秸秆运输成本与仓库建设成本则随着仓库数量的变化而变化,是可优化的变量,也是本文研究的重点[7]。此外,模型以如下假设为前提:(1) 仓库是从几个备选地点中选择的;(2) 运费由运量和运距决定;(3) 各个原料供应区域以地级行政边界为边界;(4) 各市可用作纤维乙醇生产原料的秸秆占总量的10%。
本文以山东省西北部8 个市(济南、淄博、东营、泰安、莱芜、德州、聊城、滨州) 为研究区域,利用混合整数规划模型进行仓库选址,目标是秸秆原料的总供应成本最低。这8 个市既是秸秆的供应地,也是纤维乙醇的需求地。它们在2012 年对秸秆的需求和可供应情况如表3 所示。选定的备选仓库地址分别是:济南市盖家沟物流园、淄博市良乡物流园、聊城物流园、滨州市环渤海现代物流园和禹城市。选取禹城的原因是,本文的目标乙醇生产厂就在这里,他们有小规模的仓库基础。而选择另几个物流园的原因是,在物流园建仓库符合当地政府的规划,基础设施和政策上都有利于仓库的建设。此外,模型中包括的各点之间的运输距离是从百度地图中查得的,均为实际路程距离;秸秆的单位运输成本为0.5 元/t·km,从文献中获得。该模型可以用如下综合公式(2) 表示:

表3 2012 年山东8 个地级市秸秆的需求和可供应量情况 单位:万吨

其中,C是总成本;fi表示备选仓库i的建设成本;lsi表示供应地s到备选仓库i的单位运价;Wsi表示供应地s到备选仓库i的运输量;lij表示备选仓库i到生产厂j的单位运价;Wij表示备选仓库i到生产厂j的运输量;D表示供应链中对原料的总需求量,既为了供应8 个市所需的纤维乙醇,而对秸秆产生的需求总量;Yi是表示备选仓库i被选择与否的一个0-1 变量;Ri表示备选仓库i的年吞吐能力限制。
第一个约束表明备选仓库i的建设成本由它的年吞吐能力决定,当年吞吐能力低于85 万吨时,建设成本为1 200 万,高于85 万吨时,建设成本为1 500 万。第二个约束表明备选仓库i的年吞吐量等于所有供应地对它的供应量,等于它对所有生产厂的供应量,且不超过备选仓库i的年吞吐能力限制。第三个约束表明供应地s的总供应量不超过s地的原料可供应量。
2.3 模型求解
利用上述模型求解结果是:当只有现在的生产厂时,需要分别在禹城当地和济南物流园、聊城物流园建3 个原料仓库,禹城仓库的吞吐能力约为839 441 吨,秸秆全部来自德州范围,盖家沟仓库的吞吐能力约为850 000 吨,秸秆来自济南、泰安、莱芜及淄博的一部分,聊城仓库的吞吐能力约为133 135 吨,秸秆来自聊城的一部分。最后的总成本为129 417 944.5元。
3 结 论
在现有的纤维乙醇生产厂的基础上,为了满足山东省西北部8 个市的燃料乙醇需求,需要兴建3 个原料仓库来扩大秸秆收集范围。利用混合整数规划的方法求解出了这3 个仓库的位置和吞吐能力要求,并实现了原料总供应成本的最低。本文的研究方法和结果对逐渐兴起的纤维乙醇产业的规划和现有企业的扩建有重要的指导意义。但本文是以在现有生产厂的位置扩建规模满足8 个市的燃料乙醇需求的假设为前提,进行建模求解的,对于目标生产厂的数量为两个及以上的复杂情况还有待进一步的研究。
[1] 王闻,庄新姝,袁振宏,等. 纤维素燃料乙醇产业发展现状与展望[J]. 林产化学与工业,2014,34(4):144-150.
[2] 张扬健,向威达,周涛,等. 我国燃料乙醇发展现状和趋势分析[J]. 中国能源,2009,31(1):31-33.
[3] 鲍香台,张永,林哲建,等. 生物质能供应链收集运输方式的仿真优化研究[J]. 物流技术,2011,30(12):165-168.
[4] 王兴. 基于三级供应链的物流中心选址研究[D]. 北京: 北京交通大学(硕士学位论文),2013.
[5] 蔡亚庆,仇焕广,徐志刚. 中国各区域秸秆资源可能源化利用的潜力分析[J]. 自然资源学报,2011,26(10):1637-1646.
[6] 崔明,赵立欣,田宜水,等. 中国主要农作物秸秆资源能源化利用分析评价[J]. 农业工程学报,2008,24(12):291-295.
[7] 俞宏德. 生物质电厂燃料供应系统的模拟与优化[D]. 杭州:浙江大学(硕士学位论文),2011.

