基于送货时间窗的物流配送车辆路径问题研究

赵晓婷 （兰州交通大学 交通运输学院，甘肃 兰州730070）

ZHAO Xiao-ting (School of Traffic and Transportation, Lanzhou Jiaotong University, Lanzhou 730070, China)

0 引 言

物流配送管理的核心问题就是配送车辆路径问题，而带有时间窗的配送车辆路径问题是由此演化而来的。此类问题要求车辆必须在用户规定的时间窗内对客户进行服务，每个顾客仅被服务一次，如果不能在用户规定的时间窗内完成服务则引入适当的延误惩罚。问题具有极强的现实意义，如银行运钞车调度问题、接送学生校车问题、冷鲜蔬菜海鲜配送问题[1]等，已经在配送问题的研究领域引起了很大的关注度。郭建红[2]建立了带时间窗的动态车辆路径优化模型，提出了采用两阶段法求解策略和改进型遗传算法。张炯，郎茂祥[3]建立了该问题的基于直观描述的数学模型，通过设计新的解的表示方法构造了求解该问题的禁忌搜索算法。对于带有时间窗的配送车辆路径问题采用节约算法[4-5]进行求解，混合算法[8]进行求解，论文[6-7]对此问题采用改进的遗传算法求解。

为了解决带有送货时间窗的配送车辆路径问题，本文建立了该问题的整数规划模型，并用遗传算法对模型进行求解，对实例进行计算得到最优路径配送方案。

1 带有送货时间窗的物流配送车辆路径模型

1.1 问题的描述。在配送网络中，N代表配送中心所有的用户节点N=｛1,2,…,N｝，节点0 表示配送中心车场，V表示全部的节点集V=N∪｛0 ｝，（i,j）表示弧集i,j∈V,i≠j，K=｛1,2,…,M｝表示配送车辆的集合，M表示车辆数，Q表示每辆车的最大载重量，di表示用户i的需求量，Cij表示车辆访问弧（i,j）产生的配送成本，ai表示用户i允许最早开始的服务时间，bi表示客户i允许最晚开始的服务时间，[ai,bi]为用户i的时间窗，si表示车辆到达用户点i的时刻，fi表示车辆在用户点i的服务时间，tij表示用户点i到用户点j的行驶时间，C1表示车辆早到的单位成本，C2表示单位车辆迟到的单位成本，Ci（ti）表示车辆在t时刻到达用户i时所对应的惩罚成本，引入决策变量xijk，当xijk=1 时表示车辆k访问弧（i,j），否则xijk=0。

1.2 模型假设。（1） 物品流向为单向，即纯送货；（2） 配送中心只有一个，每条线路起始点都是配送中心，配送中心和客户点的位置坐标己知：（3） 车辆为同种车型，且容量已知，在配送过程中不得超过其额定载重量，车辆数量给定，且没有行驶距离限制；（4） 每个客户必须且只能被访问一次，该点货物只能由一辆汽本完成，每辆车从车场出发最后必须返回车场；（5） 每个客户都有一个规定的时间窗[ai,bi]，送货时刻最好在此时间范围内进行，时间窗约束考虑软时间窗，即配送车辆如无法在客户指定的时间范围内完成配送任务，则要惩罚。

目标函数为：

约束条件：

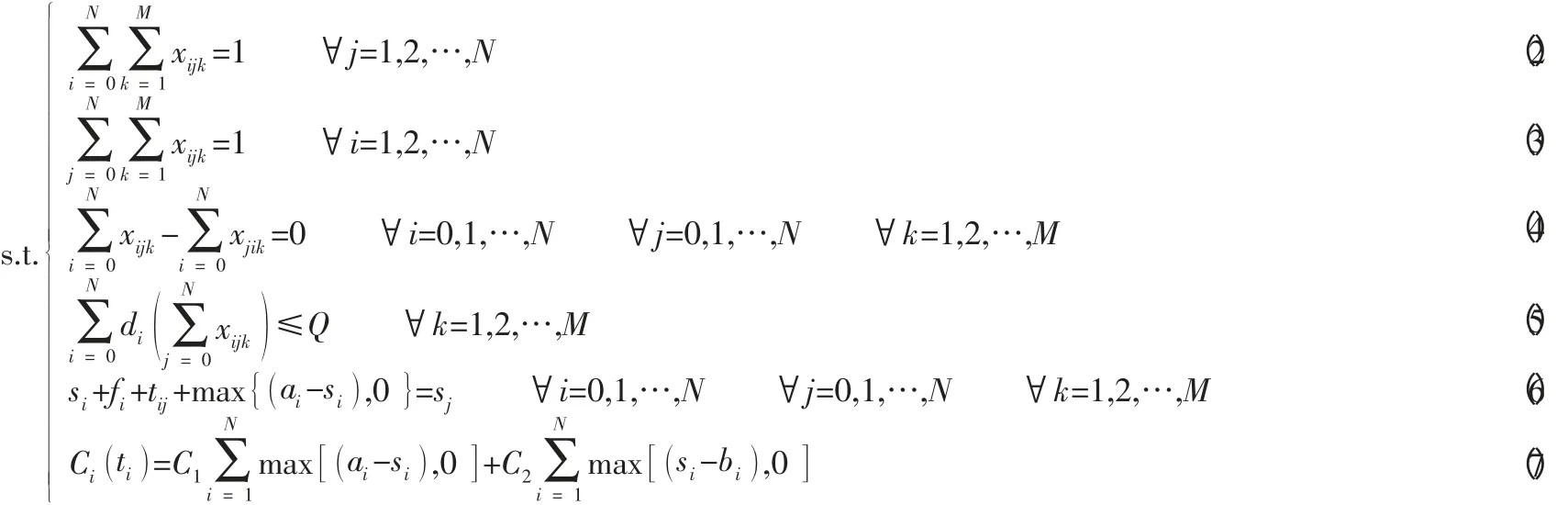
约束（2）、（3） 表示每个用户只被一辆车服务一次，约束（4） 表示车辆驶入用户i，必定会驶出用户i，约束（5） 表示载重量约束，分配给k车辆的载重量不能超过车辆载重量Q，约束（6） 为用户节点时间窗约束，约束（7） 为惩罚函数。

2 遗传算法对模型求解

遗传算法是模拟生物进化规律基于适者生存的一种自适应全局优化概率搜索算法。遗传算法构造一个适应度函数对种群进行不断的选择、交叉、变异等操作，最终获得最优解。利用该算法可以较好地解决VRP 问题。

2.1 编码。遗传算法的编码都是可理解为解的代码表现形式，VRPTW 问题的编码可以采用自然编码的方法，直接产生一组不重复的自然数的排列，该排列构成了问题的一个解，并且对应一种配送方案。根据约束可按顺序依次划分各辆车的配送路径。

2.2 适应度函数。适应度函数是评价每个染色体优劣的函数，是获得最优染色体的基本依据，一般与目标函数有密切的联系，一般目标函数为Z（x），设计的适应度函数为：

其中Cmax为一个适当相对较大的数。

2.3 遗传操作。评价函数是遗传过程中优胜劣汰的基本依据，选择优良的染色体以较大的概率进入种群，反之劣质的染色体被选入种群的概率较小。采用轮盘赌选择操作，评价函数越大，在轮盘中所占比例越大，该染色体选入种群的概率也越大。其具体选中概率为：

2.4 交叉规则。交叉是种群中的个体为父代，依照一定的规则互相交换特定位置的基因信息，从而产生继承父代大部分信息又不同于父代的子代染色体，这里具体采用双点交叉操作，在个体编码串中随机设置两个交叉点，然后再进行部分基因交换。

2.5 变异规则。采用倒位变异操作，是指随机选定连续排列中的一部分客户，将这部分客户的排列进行倒置。假设个体为123|4567|8，选中4567 部分，进行倒位操作，则通过倒位变异操作后个体就变成了123|7654|8。

3 实例应用

某物流中心分布在一个30km 的正方形区域内，有一个配送点和15 个用户，配送中心编号为0，配送中心的坐标为（20,12），用户编号依次为1,2,…,15，物流中心配有5 辆型号相同的货运车，时间窗采用24 小时制，每辆车的载重为8.5t 配送的单位距离成本为5 元/公里，货车的平均行驶速度为35 公里/小时，货车早到的惩罚成本C1为8 元/小时，迟到的惩罚成本C2为20 元/小时，计算机随机产生15 个用户坐标如表1 所示。

利用遗传算法对实例求解得到的初始优化配送方案如表2 所示。

初始优化配送方案路径如图1 所示。

各路径到达和离开用户的时间情况如表3 所示。间、出发时间以及早晚点情况。

4 结 论

针对带有送货时间窗的物流配送问题，采用遗传算法求解，建立了带有软时间窗的惩罚函数的配送整数规划模型。该模型更加贴合用户对于时间窗约束的要求，制定了结合不同实际的配送车辆路径问题的配送策略。方法原理适用性强，有一定的操作性，具有实际应用的价值，计算效率较高，可为实际的物流配送问题的解决提供参考。

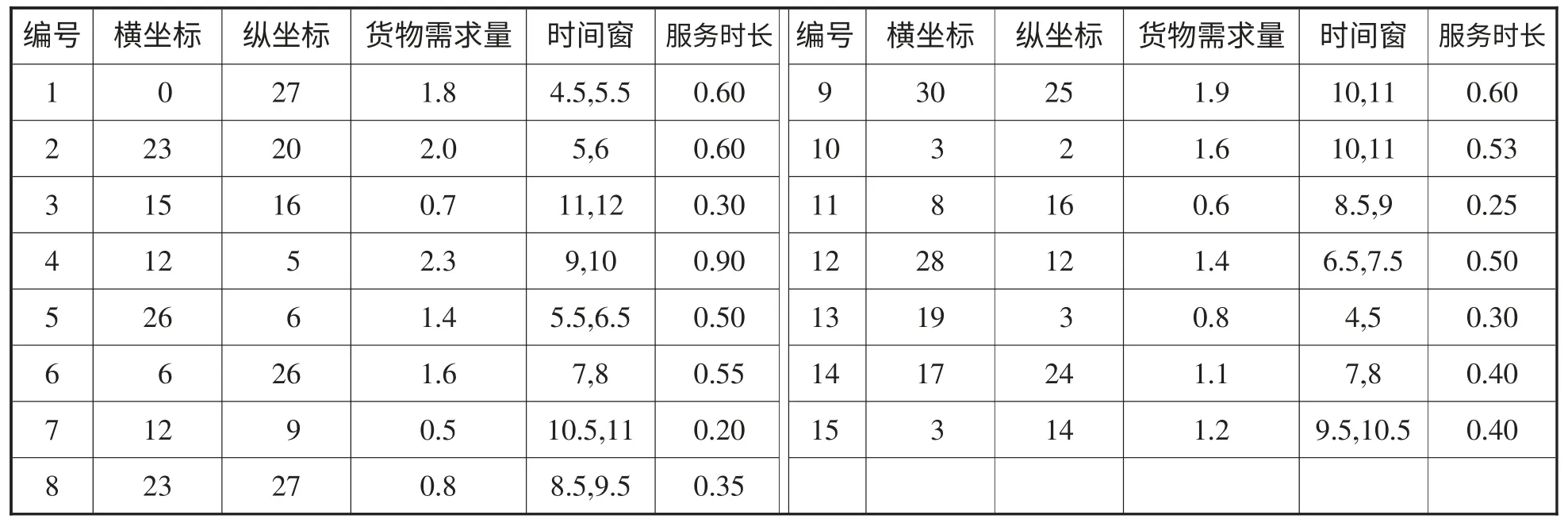
表1 客户初始信息表

表2 初始最优配送方案

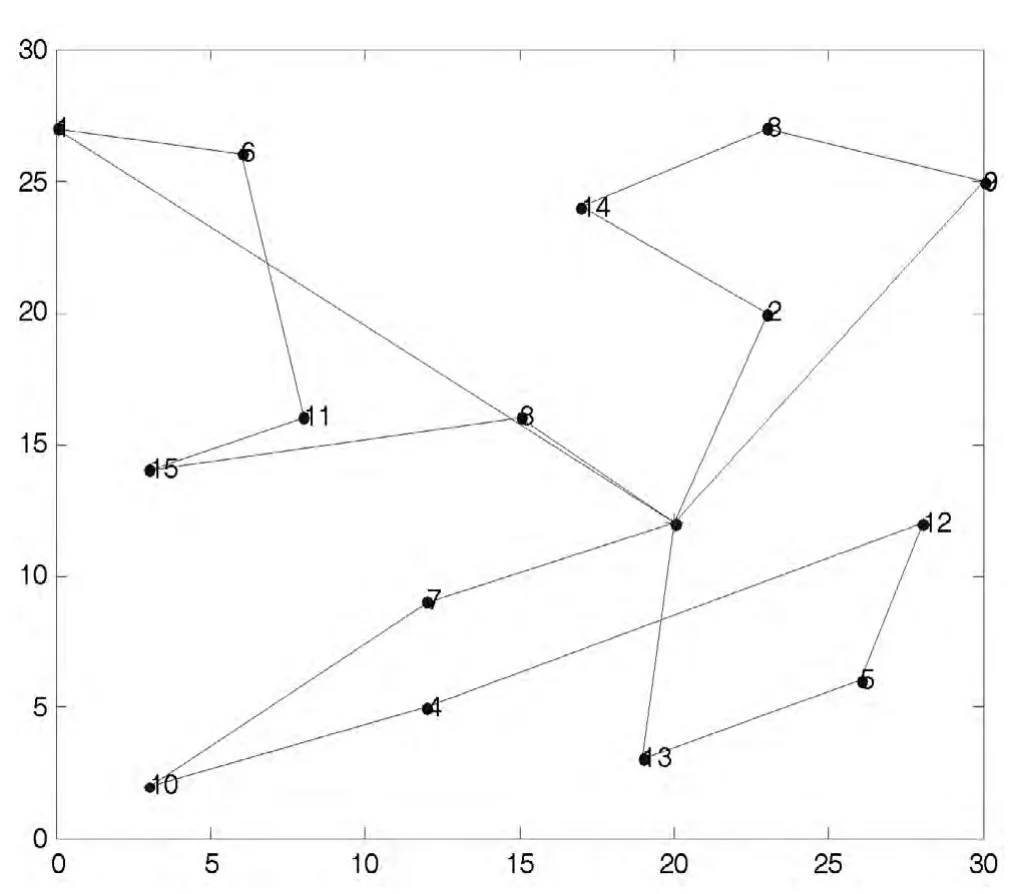
图1 初始配送方案配送路径图

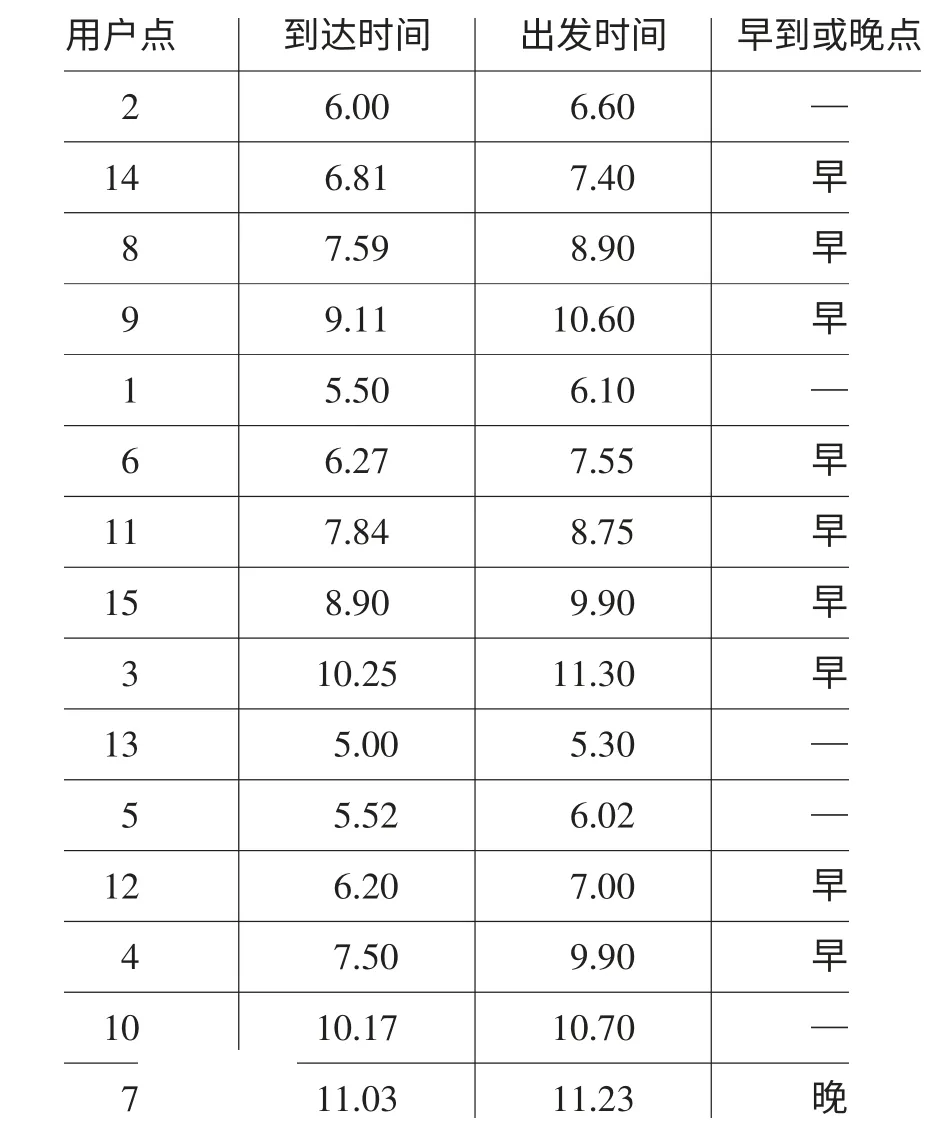
表3 子路径车辆达到和出发时间情况

[1] 潘立军. 带时间窗车辆路径问题及其算法研究[D]. 长沙：中南大学（博士学位论文），2012.

[2] 郭建红. 带时间窗的卷烟物流配送动态车辆路径优化方法研究[D]. 北京：北京交通大学（硕士学位论文），2013.

[3] 张炯，郎茂祥. 有时间窗配送车辆调度问题的禁忌搜索算法[J]. 北方交通大学学报，2004,28(2):103-106.

[4] 王海丽，王勇，曾永长. 带时间窗的易腐食品冷藏车辆配送问题[J]. 工业工程，2008,11(3):127-130.

[5] 董立娟. 带时间窗约束的冷鲜肉制品配送路径优化[D]. 长沙：中南大学（硕士学位论文），2011.

[6] 杨文超. 顾客时间窗变化的物流配送干扰管理模型及其算法[D]. 大连：大连理工大学（博士学位论文），2012.

[7] 吴红丽. 基于时间窗的家电行业物流配送路径优化问题研究[D]. 武汉：武汉科技大学（硕士学位论文），2013.

[8] 张瑞锋. 基于混合算法的带时间窗的车辆路径问题求解[J]. 计算机工程，2007(14):47-53.