考虑寻租行为的南水北调工程博弈分析

童仁义，孙绍荣 （上海理工大学 管理学院，上海200093）

TONG Ren-yi, SUN Shao-rong (Management School, University of Shanghai for Science and Technology, Shanghai 200093, China)

南水北调是中央政府早在20 世纪50 年代就提出的一项重大战略性工程。工程旨在为解决华北地区水资源缺乏、社会生产和经济发展受到重大影响等问题。通过各级泵站调度我国南方多余的水资源给一些北方地区来改变南北地区水资源量差异和由此带来的经济发展失衡的局面，从而带动并促进南北方经济生产、社会生活和人口资源环境等各方面的协调发展。工程具有难度大，涉及地域广泛、调水量大、利益相关者和中间管理部门众多等特点。南水北调工程在水资源调度和运行管理方面主要的问题有[1～2]：（1） 如何确保在调水期能够准确预测及提供受水区用水需求量合理的水和最合理的水价；（2） 工程各参与方利益的冲突对工程效率的影响问题；（3） 南水北调工程各节点的调水协调问题；（4） 水源区环境治理问题；（5） 供应链视角下，工程各调水节点的水资源库存协调控制问题等。若信息不透明和监管不到位，调水部门一旦与受水区和水源区合谋寻租，则会使上述问题更加严重，这就使得防止合谋和寻租行为的发生具有重要意义。南水北调作为一项重大的社会公共工程项目，与其他任何历史公共项目相比，既具有相似性又具有差异性。其相似性在于均是存在正的外部效应，然而由于南水北调工程的复杂性和管理多层次性导致了其管理难度比起众多其他公共项目要大很多，使得如部门之间的有效沟通和信息的有效传递等问题尤为突出，因为只有在保证各个环节的有效配合和协调，工程透明程度最大化的条件下工程才会发挥出应有的效率。而如果上述问题不能有效解决，则会滋生工程开展过程中管理部门和各工程参与方权利寻租、谋取私利以及不作为等更为严重的问题。权利寻租行为和合谋行为并不陌生，但一旦发生则会对被管理组织或项目主体的绩效等产生严重的负面影响，因为其结果是由于个体的理性导致了整体的不理性，那么应当使寻租和合谋行为在例如南水北调工程等大型公共项目中最小程度的发生或不发生，则需要相应的协调管理机制去实现这一目标，从而相应的奖惩机制设计则需要着重探讨。

1 文献综述

有关南水北调工程水资源调度和管理等问题，国内很多学者有不少研究。党志良等[3]采用博弈论的研究方法结合实证分析研究了南水北调中线某一受水区和水源区的利益冲突，证明了在合作时双方及整体利益均有增加，而在不合作时会损失同样的数值；方兰等[4]基于效率和公平从博弈角度对南水北调工程中受水地、水源地和供水单位进行了分析，并将信息成本视为中央政府补偿机制影响因子，以水资源价格为主要变量给出了在信息成本下想要达到期望的均衡结果所需的相关条件；范仓海[5]认为在市场机制情形以及由于各自利益存在矛盾，南水北调工程中的水源区与受水区之间关于补偿和投入的行为决策不存在约束双方的基本合约，只有通过第三方既中央政府的管制才会使博弈结果更加理性，使得双方采取相应环保投资或投资补偿；石智雷等[6]研究了南水北调工程利益相关者管理的利益结构，采用演化博弈方法得出了参与各方博弈均衡点，并且进化的初始条件和进化路径是重要的两个均衡影响参数，同时体现出了公共参与悖论；杨帆等[7]对南水北调工程代建制过程中的工程代理方寻租现象进行了博弈分析，最终给出一些政策建议；屈宇飞等[8]运用了演化博弈的方法，研究了南水北调工程沿线当地政府的有关策略选择，结果得出上级政府的奖惩力度不宜太高或太低；侯艳红等[9]研究了南水北调水资源供应链中的合同问题，其结论是在一定条件下共同节约合同效果好于通常的数量合同和联合投资契约，并且证明将共同节约合同和联合投资合同结合则作用最大；朱九龙等[10]对南水北调水资源供应链中水资源需求信息在各节点间不完全传递导致的牛鞭效应进行了研究，并进行了定量描述，建立了水资源供应链的动态库存模型，设计了一种牛鞭效应控制算法；王慧敏等[11]就南水北调工程中的东线工程水资源定价从供应链的角度进行了研究，建立了相应的模型并设计出基价和计量价格相结合的水价制下的动态定价约束模型，其研究表明了在联合定价模型下供应链可获得比几种传统定价方法更高的整体利益；朱九龙等[12]将供应链中VMI 库存管理方法应用于南水北调调水资源供应链的库存协调方法研究，最后通过仿真算例证明了该方法的有效性；李旭杰等[13]也从博弈论的角度，分类讨论了三种博弈情形下，水资源冲突的性质和特征并给出相应的解决措施。然而上述关于南水北调博弈问题的文献均未涉及到调水管理部门的合谋和寻租行为，本文基于南水北调工程中信息不对称下对调水部门与水源区和受水区的寻租行为从博弈论的角度进行分析，找出最优合谋概率，从而揭示寻租行为对于南水北调工程效率的影响。

2 各博弈参与方的行为策略和目标

2.1 水源区。水源区是南水北调水源头供水方。在中央政策的引导下不得不对工程进行投资和对一系列后续问题进行投入。然而由于南水北调工程会对水源区造成一系列的经济社会影响，从而水源区的目标是在保证供水的前提下最小化自己的损失和最大化自己的利益。由于调水部门的存在和信息的不确定性导致其可能和调水部门就调水价格进行合谋，故意哄抬水资源价格，并给予调水单位一定的佣金。

2.2 受水区。受水区是南水北调水资源的最终接受方。受水区的目的是能够充分利用水源区的水资源恢复和发展己方的社会生活和经济发展。那么在特定的调水期，由于信息的不对称，受水区可能与调水部门合谋虚报用水需求量并且给予调水管理部门一定的佣金。从而受水区能够最大化自己的利益。

2.3 调水部门。调水部门由于被授予一定的权利，从而可能在信息不对称的情况下分别和水源区和受水区进行合谋，造成权利寻租的发生。因为私利性的存在，调水部门的目标也是最大化自己的利益。

2.4 中央政府。中央政府是南水北调工程主要的投资方。中央政府的最大目标是确保工程的顺利建成，促进南北地区经济的均衡发展和获得最大化的社会福利。中央政府可以通过采取奖励和惩罚的方式来建立协调各方的管理机制，确保南水北调工程的有效运行。

3 博弈的前提假设

3.1 理性主体假设。假设受水区、水源区和调水部门都是理性的利益主体，其目标都是最大化自身的利益。由于私利性的存在，导致他们的行为均具有短期性和谋利性。他们的行为策略也都取决于其他两个参与方。而中央政府为了获得最大的社会福利和经济效益，其目标和行为都具有长远性和效率性。

3.2 信息的不对称性。由于南水北调工程涉及多个参与方，且工程复杂多变，从而受水区和水源区对于供给和需求的信息掌握均不完备，例如受水区对调水价格的不确定和水源区对受水区用水量的不确定。正是由于信息的不对称性才导致寻租和合谋行为的发生。

3.3 中央政府具有权威性。中央政府奖惩决策对于受水区和水源区的决策都有很大的影响。

4 博弈模型建立

4.1 调水部门的寻租行为与期望支付。为了谋取私利，调水部门会就调水价格和调水量分别与水源区和受水区进行合谋。当其与水源区合谋时，调水价格为P'，其边际调水成本为Cm，为方便讨论，假设固定调水成本为0。此时调水量为受水区的需求量V，并且调水部门会给予调水区一定的回扣S1。但由于寻租存在风险性，因为监督部门可能会披露价格和需求量等信息。因此假设被披露的风险系数为a，所付出的风险成本为Cr；当调水部门与受水区合谋时，调水价格为P（Cm＜P＜P'），边际调水成本不变。此时调水量为V'（＞V），并且受水区给予调水单位一定的佣金S2。此时，调水部门同样面临被披露风险系数a，所付出的风险成本也为Cr。由此，调水部门的期望支付如式（1） 所示。

4.2 受水区与调水部门的合谋行为与期望支付。同样是为了谋取私利，受水区会和调水部门就调水需求选择和调水部门合谋。此时，受水区有两个策略选择，即合谋和不合谋。若选择合谋，则会获得额外的水资源（V'-V），假设每单位水资源对于当地的经济和社会发展带来的现时或未来效益为（t为时间），同时得付给调水部门S2的佣金，此时调水价格为P；不合谋时不需要给予调水部门佣金。由此，受水区的期望支付如式（2） 所示。

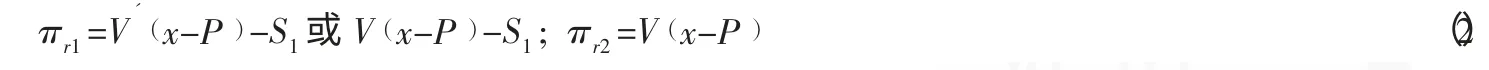
4.3 水源区与调水部门的合谋行为与期望支付。水源区为了避免因过多调水而己方利益受到损失且追求利益最大化会选择与调水部门合谋。此时水源区也有两个即合谋与不合谋。当合谋时由于价格被抬高从而会给予调水部门一定固定的回扣S1，此时按照受水区需求供水；当不合谋时，则调水部门不会给予其回扣，此时水源区正常供水，支付为0。由此，水源区的期望支付如式（3） 所示。

5 水源区、受水区和调水部门之间的博弈分析

5.1 水源区与调水部门的博弈分析。由前文分析可得水源区与调水部门博弈的博弈矩阵如表1 所示。

表1 水源区与调水部门博弈矩阵

由表1 可得当水源区合谋而调水部门不合谋和当水源区、调水部门均不合谋时双方的支付最小，为最差的策略组合。当风险系数即时，水源区必然与调水部门相互合谋，此时（合谋，合谋） 策略组合为最优纳什均衡策略组合[14]。然而，当水源区与调水部门合谋时，由于调水价格的人为上涨必然会导致受水区的利益受损，使得受水区付出高于市场价格的价格才能获得水资源。

5.2 受水区与调水部门的博弈分析。同样由前文的分析可以得出受水区与调水部门的博弈矩阵如表2 所示。

表2 水源区与调水部门博弈矩阵

5.3 水源区与受水区的博弈分析。水源区和受水区分别有两个策略选择，即与调水部门合谋和不与调水部门合谋，由上文分析可得二者的博弈矩阵如表3 所示。

表3 在无中央政府管制下水源区和受水区博弈矩阵

5.4 中央政府管制下的水源区和受水区博弈分析。由于水源区和受水区分别与供水管理部门合谋可能性的存在，使得南水北调的工程效率和社会效益由此减弱，这与中央政府作为工程主要的投资方和发起方的目标背道而驰。从而，中央政府必须通过一定的奖惩机制来终止水源区、受水区和调水部门的合谋行为。当合谋时中央政府可采取惩罚措施，对合谋一方采取惩罚，设惩罚力度为H；而对不合谋行为采取奖励，奖励力度也为H。此时由于中央政府的介入，设水源区与调水部门合谋的概率为α，则不合谋的概率为1-α。同时设受水区与调水部门合谋的概率为β，则不合谋的概率为1-β。由此，在中央政府介入下水源区与受水区的博弈矩阵如表4 所示。

中央政府通过建立奖惩制度的目的是为了促使水源区和受水区的博弈结果向（不合谋，不合谋） 转化，从而不会影响到南水北调工程的正常运作，能够保证水源区的水资源以市场价格向受水区按其正常需求供应。此时水源区的期望收益为：

表4 中央政府管制下水源区与受水区博弈矩阵

根据纳什均衡的定义和条件，要想使博弈的纳什均衡为（不合谋，不合谋），必须使在受水区的混合策略（β,1-）

β 下，水源区与调水部门合谋和不合谋的期望收益相等。要使πe1达到最大值，则要对式（1） 中α 进行求导并令导数等于0，可得：

α 下，受水区的期望收益为：

要使得πe2达到最大值，则要对（3） 中β 进行求导并令导数等于0，可得：

解式（4） 可得调水区与调水部门合谋的最优概率：

由此，在中央政府通过奖惩制度介入的情况下，水源区与受水区博弈的纳什均衡为：

由水源区和受水区博弈的纳什均衡可以得出：

（1） 当β＞β*时，则受水区会选择与调水部门合谋；当β＜β*时，则受水区不会选择与调水部门合谋；当β=β*时，则受水区会随机选择与调水部门合谋或不合谋。由于则的大小与调水区和调水部门合谋时获得的回扣S1成正比，与中央政府的惩罚力度H成反比，因而当S1越大，受水区与调水部门合谋的概率越大；当中央政府的奖惩力度H越大，受水区与调水部门合谋的概率越小。由此可见，在S1不变的情况下，中央政府可适当加大奖惩力度H，从而减小受水区与调水部门的合谋可能性。当H≥S1时，则合谋的概率为0，受水区则不会与调水部门合谋。

（2） 当α＞α*时，则水源区会选择与调水部门合谋；当α＜α*时，则水源区不会选择与调水部门合谋；当α=α*时，水源区会随机选择与调水部门合谋或不合谋。由于则α*的大小在其它条件不变时与受水区给予调水部门的佣金S2成正比。由此可见，S2越小，则合谋的概率越小，那么中央政府一方面可以通过统计和审查的措施使得水源区的调水量尽可能接近受水区用水需求量的真实值，使得S2尽可能减小，促使受水区与调水部门的合谋终止；同时，当中央政府可以通过调查等方式确定调水区对于用水量的虚报程度V'-V以及供水区与调水部门合谋时的水资源价格差P'-P，并且确定一个合理的水资源价格P和惩罚力度H，使得的值尽可能减小或者找到一个最小值，从而降低水源区和调水部门的合谋概率。

6 结 论

在信息不对称的情况下，南水北调工程的三个博弈参与方水源区、受水区和调水部门均存在机会主义倾向并且追求自身利益的最大化。此时三方可通过合谋的方式来达到目的。水源区通过与调水部门进行价格合谋来收取回扣，同时调水部门利用价格差来赚取额外的利润；受水区通过虚报水资源需求量与调水部门进行合谋，受水区因此获得更多的水资源，充分发展己方的社会经济，调水部门也因此得到受水区给予的一定数量的佣金。虽然表面上看来博弈三方的利益都达到了最大化，但水源区、受水区和调水部门的个体理性最终导致了集体的不理性，长期下去会对南水北调工程的初衷即协调南北两方的经济发展、最大化社会经济效益和南水北调工程的效率造成很大的负面影响。则问题迫切需要中央政府的介入，通过奖励和惩罚的方式来终止合谋和权利寻租行为，发挥出南水北调正常的效益。

那么，为什么合谋和寻租行为会存在？正是因为南水北调工程繁杂、涉及地域广泛、中间管理部门众多，导致水资源价格和需求量等信息存在不对称性，加之机会主义和私利性的存在，促使了合谋和寻租行为的发生。然而，虽然合谋和寻租面临着一定的风险，如前文中提到的风险系数a和被监督机构等披露后付出的风险成本Cr，但合谋和寻租是有利可图的，从而利益的驱使使得南水北调工程中的两个主要参与方水源区和供水区不会合作。因此，如果信息透明化并且寻租的风险很大且成本极高，则合谋和寻租的行为概率会大大降低。然而这需要进一步完善南水北调工程信息披露机制和监管机制，从源头上抑制合谋和寻租的发生，从而使南水北调的效率与公平能够得到保障。

[1] 河海大学技术经济研究所. 南水北调东线工程江苏段管理体制研究[Z]. 2005:56-78.

[2] 河海大学技术经济研究所. 南水北调一期工程水资源配置、调度关键技术研究[Z]. 2006:121-156.

[3] 党志良，孙建. 跨流域调水利益冲突的博弈研究——以南水北调中线陕西水源区和北京市为例[J]. 西北大学学报，2010(4):332-334.

[4] 方兰，杨伟. 南水北调工程各参与方利益补偿机制影响因素探析——公平与效率的观点[J]. 贵州财经学院学报，2012(5):60-66.

[5] 范仓海. 南水北调工程公共政策形成中的博弈分析[J]. 科技管理研究，2010(7):205-209.

[6] 石智雷，杨诚. 南水北调工程相关者管理演进与利益结构——基于进化博弈分析[J]. 科技进步与对策，2010(7):24-28.

[7] 杨帆，余建星，赵静. 南水北调工程项目代建模式下代建方寻租行为的博弈[J]. 水利水电技术，2006(1):95-97.

[8] 屈宇飞，王慧敏. 南水北调供水区污染治理策略选择的演化博弈分析[J]. 决策参考，2012(5):58-62.

[9] 侯艳红，王慧敏. 南水北调水资源供应链共同节约契约模型研究[J]. 科技进步与对策，2007(7):51-53.

[10] 朱九龙，王慧敏. 南水北调水资源供应链中牛鞭效应的随机控制[J]. 系统工程，2005(5):1-5.

[11] 王慧敏，张莉，杨玮. 南水北调东线水资源供应链定价模型[J]. 水利学报，2008(6):758-762.

[12] 朱九龙，陶晓燕，王世军. 基于VMI 理论的南水北调水资源供应链的库存协调[J]. 中国管理科学，2006(12):98-103.

[13] 李旭杰，虞玉诚. 基于博弈论的南水北调水资源调度算法研究[J]. 水利发展研究，2013(10):33-35.

[14] 王则柯. 博弈论教程[M]. 2 版. 北京：中国人民大学出版社，2010.