三种直角坐标牛顿潮流算法的收敛性比较

祁志远，肖仕武

(华北电力大学电气与电子工程学院，北京102206)

0 引言

潮流计算自出现以来在电力系统中被广泛应用。现在的潮流计算都以计算机的应用为前提，产生了很多算法［1－4］。这些算法按坐标系不同可分为直角坐标潮流算法和极坐标潮流算法两类。现阶段应用广泛的直角坐标潮流算法有常规牛顿算法、保留二阶项牛顿法和最优步距牛顿法［5－6］。文献［7－8］从理论上分析了保留二阶项牛顿法与传统牛顿算法的区别，认为保留二阶项是一种线性逼近算法，而传统牛顿算法是一种非线性的逼近算法;文献［9］认为最优步距算法将最优乘子引入到常规牛顿法当中，不仅可以改善潮流对初值的敏感性，而且可以解决病态潮流问题;文献［10］针对牛顿类潮流算法对初值敏感的问题，提出了牛顿类潮流计算的收敛定理。分析可知，很多文献都对直角坐标下不同牛顿算法的特点和性能进行过阐述［11－12］，但多限于理论分析和判断，缺乏翔实的算例。结果，导致相关认识缺乏深度和可信度。

本文首先推导了直角坐标系下传统牛顿法、保留二阶项牛顿法和最优步距牛顿法的统一数学模型，对比分析了它们的收敛特性和收敛判据。以IEEE－14、IEEE－30、IEEE－39 和IEEE－118节点等不同规模的常态系统和病态系统为对象，编写相应的MATLAB 程序，对三种直角坐标牛顿潮流算法的收敛性进行比较，得出了有意义的结论。

1 数学模型

1.1 潮流方程

直角坐标下潮流计算方程为

上述非线性方程组可表示为向量:

其中，状态量x =［e，f］T。

1.2 传统牛顿法的基本原理

将式(2)用泰勒级数展开，并略去二阶项及以上高阶项，得到迭代格式

此种方法为传统牛顿法。

1.3 保留二阶项牛顿法的基本原理

由式(1)知，潮流方程是以状态变量e 和f 来表示的一组二次代数方程式。对这组方程进行泰勒级数展开后，不存在二阶以上的高阶项。因此，在保留其二阶项后，就得到一组没有截断误差的精确表达式。

将潮流方程组f(x)，在x 附近利用泰勒级数进行展开，则有

式中H 为二阶项，故可得到迭代格式

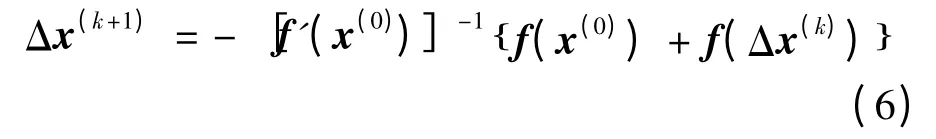
1.4 最优步距牛顿法的基本原理

以牛顿法所得的修正量为最优步距方向，即

为了调整步距，用μ 修正步长，于是式(5)将变为

记:

则式(8)可写作:

所求目标函数为

即

其中，

式(13)的解就是使F 有最小值的最优步距因子μ*。

于是可调整第k 次迭代的修正量Δx(k)得到最优的步距为

2 收敛判据比较

由于常规牛顿法、保留二阶项牛顿法和最优步距牛顿法在对初始估计值x(0)的处理上采用了不同的方式，以致这三种方法的Δx 含义也不完全相同。其差别可用图1 中的迭代过程说明。

从图1 可知，在传统牛顿法中，由于每次迭代后的估计值都在改变，即自x(0)→x(1)→… →x(k)，所以其Δx(k)是以新的估计值作为基准而得到的修正值;在保留二阶项牛顿法中，由于估计值x(0)保持不变，所以Δx(k)总是以初始估计值x(0)作为基准而得到的修正值;在最优步距牛顿法中，其迭代过程类似于常规牛顿法，只不过其修正值Δx(k)变为最优步距Δx*(k)。

图1 Δx 的比较Fig.1 Comparison of Δx

由于存在上述差别，三种直角坐标牛顿算法的收敛判据也是有区别的。

常规牛顿算法的收敛判据为

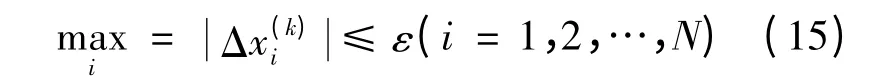
即每次迭代的误差小于某一数值停止迭代。

保留二阶项牛顿法的收敛判据为

即本次迭代与上次迭代的误差之差小于某一数值停止迭代。

最优步距牛顿算法的收敛判据为

即每次迭代的最优步距小于某一数值停止迭代。

由于常规牛顿法和最优步距牛顿法每次迭代都需更新雅可比矩阵，而保留二阶项牛顿法只需计算一次雅可比矩阵，故计算速度较快;最优步距牛顿法由于引入最优乘子，潮流总是收敛的。

3 常态系统潮流算法收敛性比较

本文以IEEE14、IEEE30、IEEE39 和IEEE118 系统进为测试对象，所选收敛精度为修正量最大值小于10-8(收敛精度是以100 MW 为基准功率的标幺值)。分别对三种潮流计算方法进行测试，收敛次数和计算时间的测试结果如表1所示，其中IEEE39节点的半对数坐标收敛曲线如图2所示。

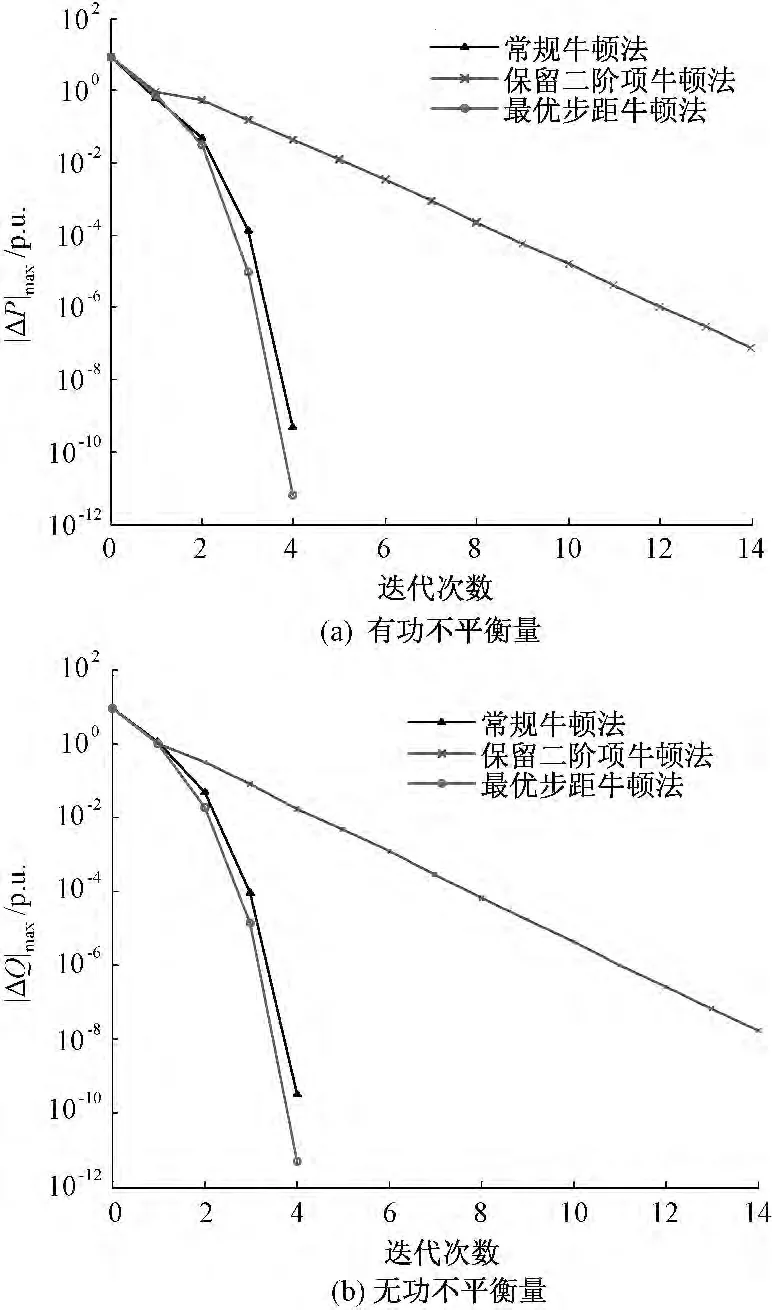
图2 常态系统不平衡量收敛曲线Fig.2 Convergence curves of deviation for normal system

由图2 可知，常规牛顿法和最优步距牛顿法的收敛速度接近，即按抛物线型收敛。由于最优步距因子的调整，最优步距牛顿法收敛性好于常规牛顿算法，同样为4 次收敛，最优步距牛顿法的最大有功功率不平衡量明显小于常规牛顿算法。而保留二阶项的牛顿法收敛速度较慢，收敛曲线基本为直线。

表1 常态系统的潮流收敛情况Tab.1 Convergence of power flow for the normal system

表1 的结果表明:对于相同的收敛精度，不同的测试系统，常规牛顿算法和最优步距牛顿法收敛次数比较稳定，几乎不随系统规模的增大而增加。但是保留二阶项牛顿法就不一样，随着系统规模的增加，迭代次数迅速增加。然而，保留二阶项牛顿法所需的计算时间最短，所以保留二阶项牛顿法的计算速度较传统牛顿法和最优步距牛顿法还是快得多。

为了测试不同收敛精度对收敛情况的影响，对IEEE39 节点系统选用不同的收敛精度，得到表2所示的计算结果。

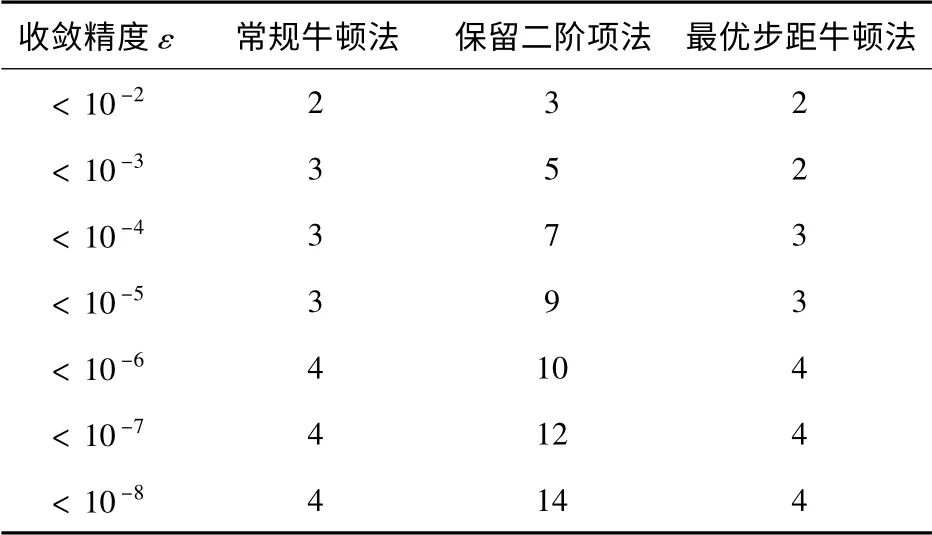
表2 IEEE39 节点系统的潮流收敛情况Tab.2 Convergence of power flow for IEEE－39 nodes system

表2 表明:随着收敛精度的提高，保留二阶项牛顿算法的迭代次数逐渐增加，而常规牛顿法和最优步距牛顿法的迭代次数几乎不随收敛精度变化。

4 病态系统潮流算法收敛性比较

以IEEE39 节点系统为算例，采用同步增加所有负荷节点有功和无功负荷的方法使其病态化，负荷从1.1 倍逐渐增加至1.5 倍的常态负荷，收敛精度取10-8，计算结果如表3所示。

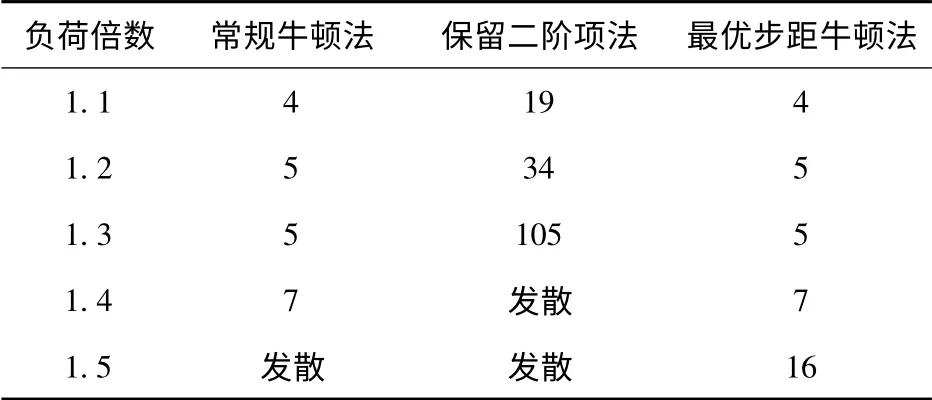
表3 不同负荷下的潮流收敛情况Tab.3 Convergence of power flow under different loads

由表3 知，常规牛顿法在负荷增加到1.5 倍常态负荷时开始不收敛，并呈现周期性振荡现象;在收敛的情况下，其迭代次数基本保持不变。保留二阶项牛顿法从1.2 倍常态负荷增加到1.3 倍时，收敛特性迅速变坏，迭代次数从24 次迅速上升为105 次，在负荷增加到1.4 倍的常态负荷时，开始不收敛。最优步距牛顿法始终收敛，在1.5倍常态负荷条件下，其迭代次数增加为16 次。另外该方法，在第5 次迭代后，最大功率偏差基本保持不变。可见最优步距牛顿法收敛特性最好，有较强的适应病态系统的能力;保留二阶项牛顿法适应病态系统的能力最差，对病态系统反应非常灵敏。图3 给出了1.5 倍常态负荷下三种算法的半对数坐标收敛曲线。

由图3 可知，在1.5 倍的常态负荷时，常规牛顿法振荡发散，保留二阶项牛顿法线性发散，最优步距牛顿法则收敛。

图3 病态系统不平衡量收敛曲线Fig.3 Convergence curves of deviation for illconditioned system

需要指出的是，最优步距牛顿法在1.5 倍常态负荷下，对IEEE39 节点系统，虽收敛，但收敛精度较差;对IEEE30 节点系统，加重30 节点的负荷使其病态化，收敛过程类似于IEEE39 节点系统，但收敛精度较好，最大功率偏差接近10-2。

5 结论

本文在推导了直角坐标系下传统牛顿法、保留二阶项牛顿法和最优步距牛顿法的统一数学模型的基础上，对三种潮流算法的收敛性进行对比测试。结果表明:对常态算例系统，三种算法均收敛，其中保留二阶项牛顿法迭代次数最多，但计算用时最短;对同样的迭代次数，最优步距牛顿法收敛精度最高。对重负荷病态算例系统，随着负荷的增加，保留二阶项牛顿法迭代次数急剧增加，最早丧失收敛性且以单调形式发散;常规牛顿法迭代次数增加不明显，收敛性丧失迟于前者、以振荡形式发散;最优步距牛顿法始终收敛于可行解且迭代次数基本不变，表现出了良好的收敛性。计算结果可为实际潮流算法的选取提供有益的参考。

［1］王祖佑.电力系统稳态运行计算机分析［M］.北京:水利电力出版社，1987.

［2］Chen Ying，Shen Chen.A Jacobian-free Newton-GMRES (m)method with adaptive preconditioner and its application for power flow calculations［J］.IEEE Transactions on Power Systems，2006，21 (3):1096－1103.

［3］智勇，拜润卿，梁福波，等.计及发电机励磁调差系数的潮流计算方法分析［J］.现代电力，2014，31 (5):32－36.

［4］刘宇，高山，杨胜春，等.电力系统概率潮流算法综述［J］.电力系统自动化，2014，38 (23):127－135.

［5］王守相，刘玉田.电力系统潮流计算研究现状［J］.山东电力技术，1996，(5):8－12.

［6］陈珩.电力系统稳态分析(第三版)［M］.北京:中国电力出版社，2007.

［7］王宪荣，柳焯，张伯明.非线性总项与保留非线性潮流算法的拓广［J］.哈尔滨工业大学学报，1990，(6):60－66.

［8］刘广一，胡锡龙，于尔铿，等.电力系统病态潮流计算新算法［J］.中国电机工程学报，1991，11(S1):27－36.

［9］王宪荣，包丽明，柳焯.极坐标系准最优乘子病态潮流解法研究［J］.中国电机工程学报，1994，14(1):40－45.

［10］孙秋野，陈会敏，杨家农，等.牛顿类潮流计算方法的收敛性分析［J］.中国电机工程学报，2014，34 (13):2196－2200.

［11］林济铿，吴鹏，袁龙，等.基于张量法的电力系统潮流计算［J］.中国电机工程学报，2011，31(34):113－119.

［12］李敏，陈金富，段献忠，等.潮流计算收敛性问题研究综述［J］.继电器，2006，34 (4):74－79.