参照群体对行人从众过街行为决策的影响*

吴文静 罗清玉 贾洪飞

(吉林大学 交通学院，吉林 长春130025)

“中国式过马路”是我国城市交通的一大顽症，并已成为困扰交通管理者的一大难题.过街行人往往成群出现，当他们在决定何时过街、以什么速度过街等问题时通常会参照他人的行为决策，由于受到他人行为的影响，个体往往会偏离自己原先的选择意愿而做出符合群体行为偏好的决策.行人的这一行为现象可以借用行为科学中的群体参照理论进行解释，此时的参照群体，为同处于交叉口环境下的将要过街的其他行人.由于参照效应的潜在作用，行人会从众过街，尤其是在有行人信号灯交叉口处，在红灯期间常出现群体违章过街行为，这些行为是交叉口处潜在的安全隐患.要改善行人交通安全需要从多方面入手，例如对行人合理过街行为的有效引导、教育，对行人过街设施的优化布置和设计.显然，在采取上述措施之前，必须清晰、完整地掌握行人的过街特性，以保证措施的有效性.

国内外研究学者就行人从众过街问题已有较多的文献出现，例如Zhou 等［1］分析了中国行人在与他人过街行为一致以及不一致两种情况下的行人的主观规范和行为控制，并提出了行为干预对策;Santor等［2］发现同龄人，尤其是青少年群体容易发生从众过街行为;McGhie 等［3］探究了团体认同性和从众水平之间的关系，结果表明当和朋友在一起并且当朋友要闯红灯过街时，行人自身违规过街的意图会明显增强;此外，交叉口处过街人群的密度、群体规模也会影响行人的从众过街行为［4-5］.而国内针对参照群体对行人过街行为影响的研究尚未见到公开发表的文献.从现有的研究资料来看，对于行人从众过街行为的研究多集中于观察阶段，从定量角度衡量参照效应的作用机理尚待研究.基于此，文中以路口行人从众过街行为为研究对象，对从众过街的行为诱因、行为特性等进行深入研究，提出科学合理的解决方案.

1 从众过街行为的影响因素

从众行为可分为两种形式:理性从众和非理性从众，非理性从众即为盲从;而理性从众表明在与他人面对相同的过街环境时，个体受到他人行为影响的同时，自身也会有行为判断过程.在此，假设过街行人为理性人，那么其过街行为影响因素可以划分为以下3 个方面.

1)个体特征.从个体自身角度出发，个体对交叉口的了解程度、性别年龄、过街速度、出行目的、行人过街等待时长等因素都会对其行为决策产生影响.

2)参照群体特征.群体对行人个体行为决策的影响是文中研究的重点，影响从众行为的群体特征因素主要有群体的凝聚力、一致性、规模、成员构成特征等.

3)交叉口的周围环境对行为过街决策也是重要的影响因素之一.例如有信号交叉口或无信号交叉口，行人过街行为决策不同.二次过街的交叉口、道路中央的安全岛设置情况、过街宽度、车流量的大小以及车辆对行人的避让情况等同样也是影响行人行为过街行为决策的重要因素.

2 参照群体对行人过街行为决策的影响途径

过街行人依据其行为可划分为3 种类型:违章者、遵章者和从众者，其中从众者最终会选择违章或遵章过街而与其他两类行人的行为决策相关，且这两类群体对个体的影响效果不同，作用强度也不同.在此运用博弈论的方法进行分析.

在行人过街行为博弈中，博弈的一方是行人，另一方是机动车辆.在行人到达交叉口时，并不知道车辆会避让或是不避让，所知道的是在不同的驾驶员行为决策下，行人采取通过或等待行为的得益，在此给出得益矩阵，如表1所示.其中，r 为由于冲突而产生的潜在风险损失，t 为由于等待而产生的时间延误，Px为行人通过的概率，Pp为驾驶员避让的概率.在此博弈下，选择通过的行人的期望得益为u1= r·(Pp-1)Px;选择等待的行人的期望得益为u2=- t·(1 -Px).因此，行人群体的平均期望得益为

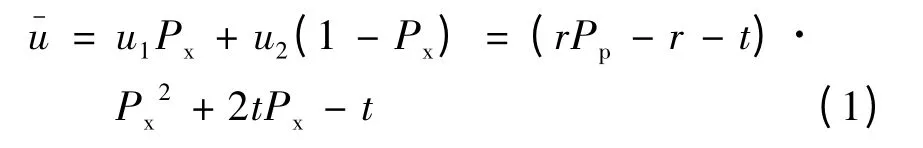
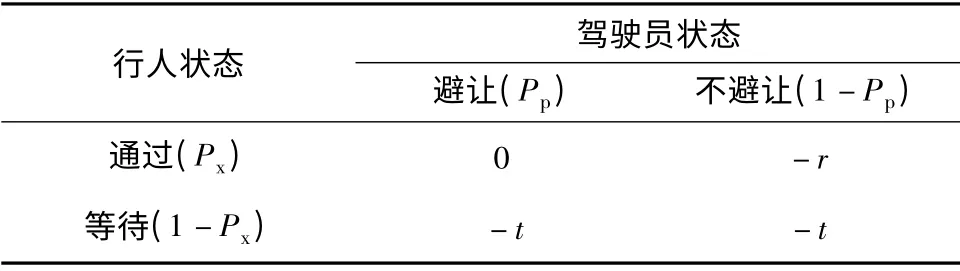
表1 得益矩阵Table1 Benefit matrix

将群体的平均期望得益作为群体对个体行为决策的影响力.在这个力作用下，个体过街行为决策会偏移其孤立状态下所做的行为决策，影响着个体的通过意愿或者等待意愿.根据博弈的动态均衡理论，行人群体通过多次动态博弈，最终到达稳定状态.当考虑到行人的通过概率Px随时间t'的动态变化Px(t')时，Erwin 采用复制动态方程形式来描述群体行为的演变过程.在此，直接考虑行人在交叉口处的通过收益与等待收益之间的差异，得到如下结果:

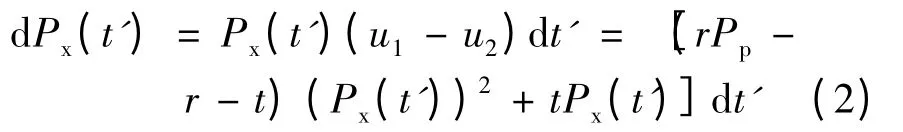
由式(2)可知，如果行人通过的期望收益大于等待的期望收益，那么随着时间的推移Px(t')会增加，反之减少.求解(2)的方程解，得到Px(t*)=0为方程的一个均衡解，表明所有的行人都在交叉口处等待，此时没有其他行为的行人干扰，系统是均衡的.另一个解为Px(t*)=t/(t +r -rPp)，由进化博弈理论可知，F(t)=dPx(t)/dt，不难得到F'(0)＞0，因此行人都等待并不是交叉口的稳定状态;而另一个解处的导数为，因此通过行人的比例为为该博弈的进化稳定策略.从这个比例值的结构可知，当机动车都避让时，即Pp=1 时，行人都通过;当机动车都不避让，即Pp=0 时，仍然会有的行人选择通过，此时行人通过的比例与该交叉口处通过的风险损失有关，当风险值远远大于过街等待所产生的效用时，通过的行人会大大降低.

3 参照群体影响下行人过街行为决策的阈值模型构建

3.1 行人从众过街决策过程分析

作为微观扩散模型之一，阈值模型用来描述个体受外界影响的累积效果具有很好的代表性.分析过街行人个体的行为效用，主要包括3 个部分:行人自身效用评价、群体效用拉动以及随机影响因素.文中，主要研究受他人行为影响后，做出通过决策的行人，即从众过街的行人.由于每个人通过的意愿不同，有些人即使没有他人行为影响，同样也会做出通过决策.有些人则是在他人行为影响下才有通过意愿，并且在群体效用拉力的作用下，个体通过的意愿会逐渐增强，并最终超过某一阈值而做出通过的决策.在此将行人自身效用u1、群体效用作用S2、过街阈值C 的关系列举如下，同时分析不同关系下行人的过街行为.

u1，t-1、u1，t分别表示在t -1 时刻、t 时刻的不受群体影响的行人自身的行为决策;S2，t-1、S2，t表示在t-1 时刻、t 时刻其他行人群体对个体行人行为决策的影响.

情况1 u1，t＞C，在t 时刻，不受群体影响，行人做出通过行为;

情况2 u1，t-1+S2，t-1＜C，u1，t+S2，t＞C，在t -1时刻，行人在自身及群体的影响下并没有产生通过意愿，随着群体拉力效应增强，在t 时刻行人做出通过行为;

情况3 u1，t-1+S2，t-1＜C，u1，t+S2，t＜C，表明群体对个体的作用并没有超出个体通过的阈值，个体仍然选择等待.

3.2 行人从众过街阈值模型结构

在从众阈值模型中，当个体的总效用评价值超过个体自身设定的某一判断阈值时，从众通过行为便可能产生.借鉴扩散传播理论，并结合行人决策过程分析，采用效用函数模型构建参照群体影响下的行人过街行为决策模型:

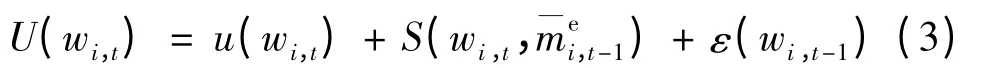
式中:wi，t为个体i 在时刻t 的过街行为决策，其为二元变量，通过时取1，等待取值为-1;U(wi，t)为第i个行人在t 个步长对过街行为的效用评价;u (wi，t)为行人不受他人影响下的自身的可观察的行为效用;为群体对个体行人的效用;为行人群体的期望收益;ε(wi，t-1)为个体i 在t -1个步长后所受到的随机影响.

由于个体的行人效用与群体的效用最终达到动态均衡，因此个体效用变化与群体平均效用的变化方向一致.即，因此可将群体效应的表达式描述为因此构建行人过街行为的二项logit 模型［6］:

式中，β 为非随机项的比重，vj，t为行人j 在t 时刻的过街行为决策.从此可见，当β 趋于∞时，随机项ε将忽略;当β 趋于0 时，行为完全随机产生，那么行人通过或等待的概率分别为1/2.此外，当J =0 时，行人过街模型演变为标准的二项Logit 模型，个体过街决策取决于其初始效用u(wi，t).

3.3 模型的解析

从式(4)中提出了行人过街行为决策的理论模型，分别由行人自身效用、他人效用、随机效用构成了行人的决策.其中由Logit 模型的效用函数结构可知，u(wi，t)可表达为常数项k 与函数项h 的线性模型.在此对此表达式进行转换，取u(1)=h+k，u(-1)= -h+k，因此h =1/2(u(1)-u(-1)).由此，当h ＞0 时，表明由自身效用评价来说，行人倾向于通过;h ＜0 则表明，行人更倾向于等待;当h =0 时，行人自身没有倾向，那么由式(4)可知，行人完全受群体偏好的影响.此外，根据扩散理论与第3 节中所描述系统进化稳定策略，当个体的期望收益与群体的期望收益一致时，个体的行为也将处于稳定状态.基于上述分析过程，首先推导个体的期望收益:

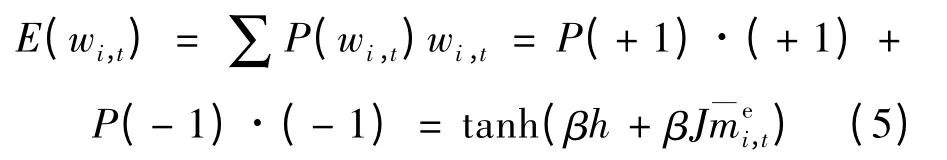
假定个体的主观期望与群体期望相一致，即E(wi，t)=，将此时个体的期望收益用m*表示，则方程(5)转变为

运用Matlab 解析上述方程，m*的取值与βJ、βh的取值有关，并且存在以下3 种情况.

1)βJ ＞1，且h =0，表明行人完全跟随他人行为.此时方程的解析如图1(a)所示.其中横轴表示个体主观期望为从众通过的人群比例，纵轴表示群体中接受通过的人群比例，其中45°分割线表示个体主观期望与群体期望完全相等.图1(a)中存在3个交点表示系统平衡的3 个解，P-＜Pm＜P+，P-表示系统中大部分行人是选择等待的，只有概率为P-的行人会选择从众通过;P+表明系统中大部分行人选择通过;Pm介于两者之间，但根据理论推导［7］，Pm这个解并不稳定，最终行人会在群体作用力的驱使下趋向于P-或P+.

2)当βJ ＞1，且h≠0，表明行人在受到他人行为的影响的同时也会评估自身的效用，行人在两者作用力的影响下做出行为决策.根据两者作用强度的不同，会出现以下两种情况.需要将βh 的取值与阈值x 相关的表达式进行比较.

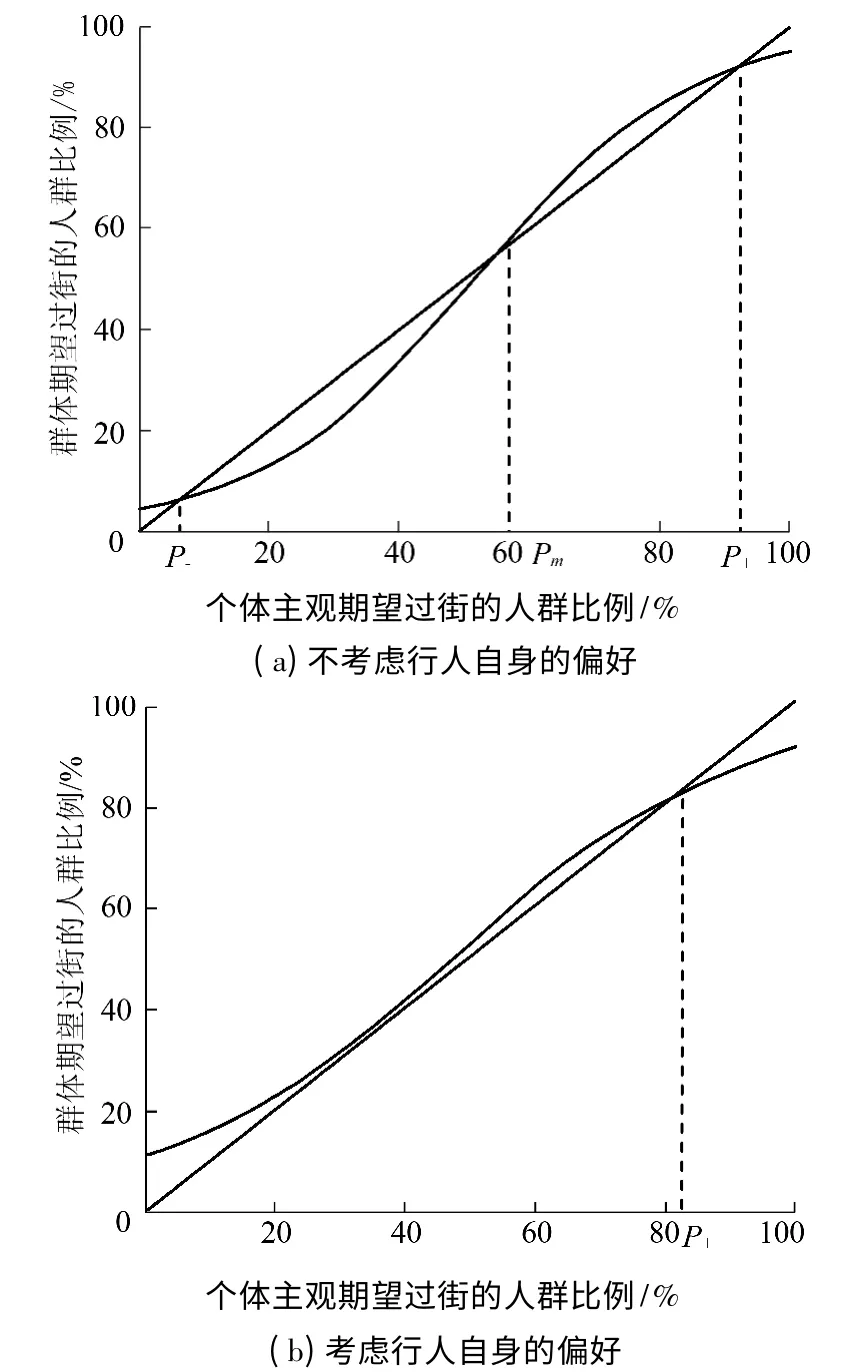
图1 行人过街行为的变化趋势Fig.1 Variation trend of the decisions of pedestrians crossing behavior

3.4 模型的应用

选取长春市自由大路与同志街交汇处的信号交叉口为研究对象，其人行横道长22m，宽7m，信号灯周期为180s，其中直左相位55s，直行相位74s，左转相位42 s.由于临近商业街，步行过街行人较多，且结伴人群多.通过视频观察，发现此路口闯灯过街现象严重，尤其是在高峰时段，若有一位行人闯灯，在紧接着的2 s 内一定会有跟随者，这对于交叉口的机动车通行存在着严重的干扰.为了能清晰地观察个体的行为决策过程，尤其是从众行为，在此选择了非高峰时间，在下午1:30 ～3:30 进行观察，对采集的视频数据进行时间导入及图像分析.

对行人从众闯灯过街行为进行观测，并选取个体过街行为决策的影响因素，包括个体的年龄x1、等待时长x2、是否有孩子x3、结伴人数x4，他人的行为影响定义为某一时刻，交叉口过街群体中，通过或等待的行人占群体人数的比例，这一比值随着行人群体行为的动态变化而变化.在此，将个体初始效用u(wi，t)的函数形式表达如下:

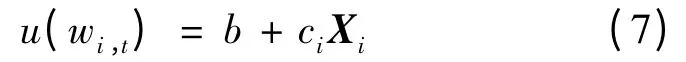
式中，b 为常数项，ci为变量的系数，Xi为变量向量.将式(7)代入式(4)，为了简化计算，在此取β =1，由此得到行人过街行为决策的二项Logit 模型，见式(8).对模型进行参数的极大似然估计，得到标定结果如表2所示.

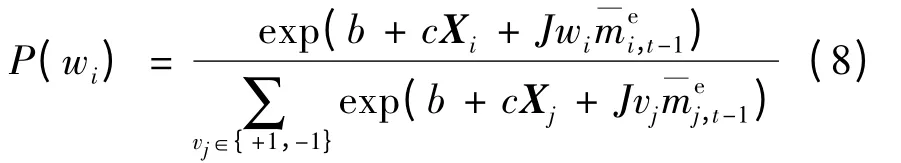
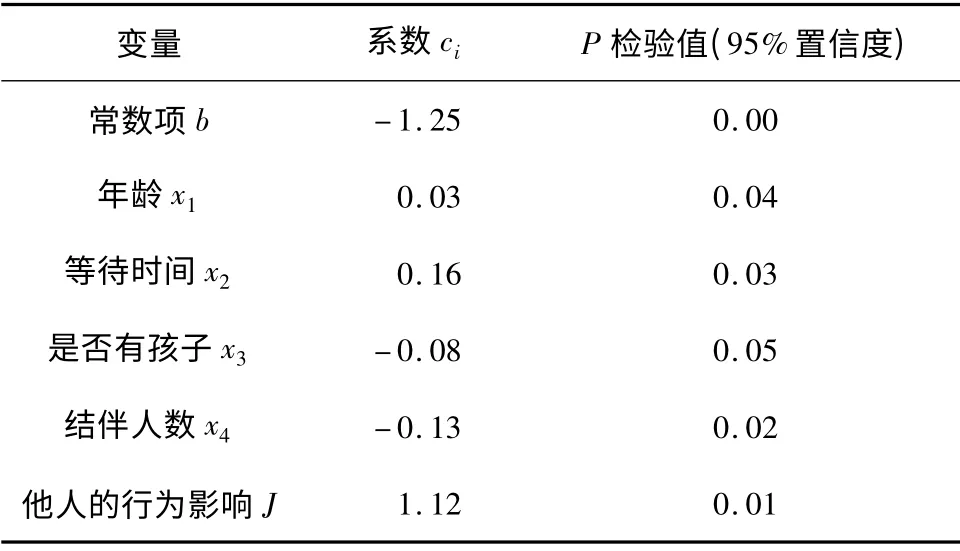
表2 行人过街的二项Logit 模型标定结果Table2 Estimated results of binary Logit model of pedestrians crossing

由标定结果可知，年龄越大，从众闯灯过街的倾向越大;如果是抱小孩的行人或者是有儿童同行，或者是行人与朋友或家人结伴而行，行人从众闯灯的行为也会降低;而随着等待时间的增加，行人从众闯灯过街的倾向增加.此外，通过检验，他人的行为决策对行人自身的过街行为决策影响显著.

对结果进行分析，选择某一特征行人群体为研究对象，假设其年龄为25 岁左右，在交叉口等候时间大约为3 min，没有领孩子，没有同伴，将此代入式(6)中，解析m*= tanh(-0.15 +1.12 m*)时的解，通过方程解析得到在此交叉口，在等候3 min 以后，交叉口的平衡态是25 岁左右的行人有22%选择闯灯通过，如图2所示.上述只是对某一类群体进行分析，通过对此交叉口的所有类别行人进行闯灯行为分析，就可得到以此交叉口过街行为群体为参照类的平衡态下行人闯灯过街的比例值.并且通过对比不同交叉口的闯灯比例值就能发现某些交叉口存在的潜在安全问题，并有针对性地对此交叉口的行人交通设施进行改进.

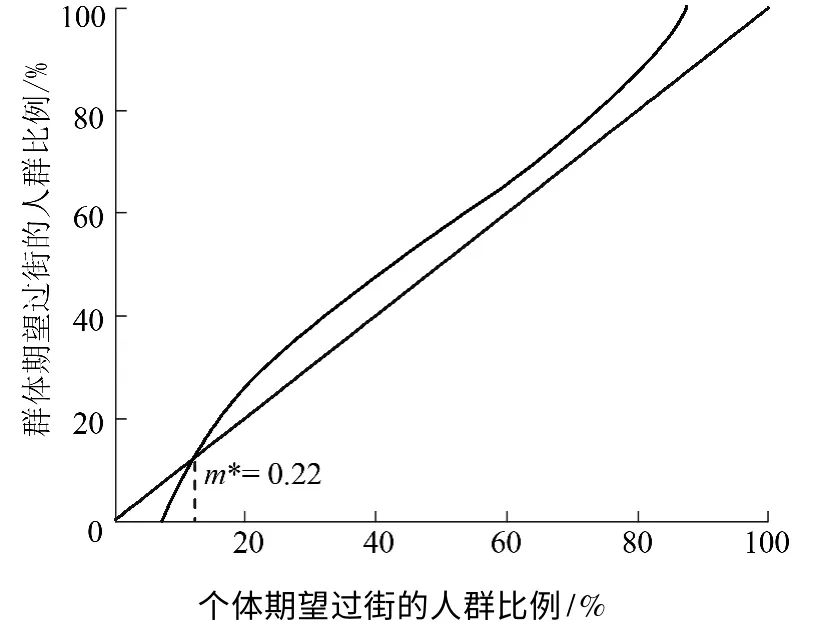
图2 某一类群体过街行为选择变化规律Fig.2 Variation trend of choice of one type of pedestrians crossing behavior

4 行人从众过街干预和引导策略分析

行人过街行为决策与政策、规划、设计、管理等众多因素有关，减少行人从众过街率是一个系统问题.需要政府部门关注行人过街问题，完善过街设施，同时加强对违章行为的处罚力度.

从过街设施角度考虑:①在过街需求大的路段设置过街设施，尽量靠近主要吸引点设置，必要时也可以考虑立体过街;②某些交通量较大的交叉口，行人二次过街的概率最大，因此合理的安全岛设置能够比较好地满足行人过街要求，减少从众过街的几率;③设计行人过街的可变信号配时方案，在早晚高峰时间，给行人尽可能多的通行权，而不要把所有的焦点都集中于机动车.

从对过街行人管理考虑:①在有需要的过街处，设置协管管理，或设置电子探头对违章行人进行监测，让行人自觉遵守交通行为规范;②在重要过街处或事故多发地，对违章行人进行严厉的处罚，特别是对于带头违章过街的行人，处罚力度加大，从而遏制行人挑战性的违章态度.

5 结论

参照群体广泛应用于社会学、消费者行为学等领域，将其应用于交通行为的研究并不多见，文中引用参照群体效用理论，分析交叉口处行人从众过街行为.

(1)在分析行人过街行为决策影响因素的基础上，应用动态博弈理论解析了参照群体对行人过街的作用途径;

(2)构建参照群体影响下行人过街行为决策的阈值模型，提出模型结构，分析模型可能出现的3 种情况，并探讨了在不同解下的行人过街行为.以长春市某一交叉口为例，应用模型分析了在此交叉口环境下行人从众过街行为.

(3)在交叉口的行人过街数据处理过程中，对行人从众判断的方法有待于改进.且由于交叉口处交通环境、过街设施设置等差异，行人过街行为也会随之变化，因此有必要选择多个有代表性的交叉口进行比较分析.

［1］Zhou R G，Horrey W J.Predicting adolescent pedestrians’behavioral intentions to follow the masses in risky crossing situations［J］.Transportation Research Part F，2010，13(4):153-163.

［2］Santor D A，Messervey D，Kusumakar V.Measuring peer pressure，popularity，and conformity in adolescent boys and girls:predicting school performance，sexual attitudes，and substance abuse［J］.Youth and Adolescence，2000，29(2):163-182.

［3］McGhie A，LewisI，Hyde M K.The influence of conformity and group identity on drink walking intentions:comparing intentions to drink walk across risky pedestrian crossing scenarios［J］.Accident Analysis and Prevention，2012，45(1):639-645.

［4］Rosenbloom T.Crossing at a red light:behaviour of individuals and groups［J］.Transportation Research，Part F，2009，55(4):389-394.

［5］Zhuang X，Wu C.Pedestrians’crossing behaviors and safety at unmarked roadway in China［J］.Accident Analysis and Prevention，2011，31(7):1927-1936.

［6］Daisuke Fukuda，Shigeru Morichi.Incorporating aggregate behavior in an individual’s discrete choice:an application to analyzing illegal bicycle parking behavior［J］.Transportation Research，Part A，2007，14(5):313-325.

［7］Brock W，Durlauf S.Discrete choice with social interactions［J］.Review of Economic Studies，2001，68(9):235-260.

［8］翁小雄，黄德剑，黎升福.公共建筑行人交通仿真性能分析［J］.华南理工大学学报:自然科学版，2012，40(2):45-49.Weng Xiao-xiong，Huang De-jian，Li Sheng-fu.Performance analysis of simulation of pedestrian traffic in public building［J］.Journal of South China University of Technology:Natural Science Edition，2012，40(2):45-49.

［9］王子甲，陈峰，施仲衡.基于Agent 的社会力模型实现及地铁通道行人仿真［J］.华南理工大学学报:自然科学版，2013，41(4):90-95.Wang Zi-jia，Cheng Feng，Shi Zhong-heng.Agent-based realization of social force model and simulation of pedestrians in subway passageway［J］.Journal of South China University of Technology:Natural Science Edition，2013，41(4):90-95.

［10］陈坚，晏启鹏，杨飞，等.出行方式选择行为的SEMLogit 整合模型［J］.华南理工大学学报:自然科学版，2013，41(2):51-65.Cheng Jian，Yan Qi-pong，Yang Fei，et al.SEM-Logit integration model of travel mode choice behaviors ［J］.Journal of South China University of Technology:Natural Science Edition，2013，41(2):51-65.

［11］俞礼军，王蕾云.MNP 模型参数估计实用方法及其在出行方式预测中的应用［J］.华南理工大学学报:自然科学版，2014，42(2):103-108.Yu Li-jun，Wang Lei-yun.Practical method of MNP model parameter estimation and its application to forecast of trip mode choice［J］.Journal of South China University of Technology:Natural Science Edition，2014，42(2):103-108.

［12］周家中，张殿业.多模式交通网络下的城市交通出行链行为模型［J］.华南理工大学学报:自然科学版，2014，42(2):125-131.Zhou Jia-zhong，Zhang Dian-ye.Behavior model of urban trip chains in multi-mode transportation network ［J］.Journal of South China University of Technology:Natural Science Edition，2014，42(2):125-131.