复杂机电产品线缆信息本体表达与存储分析

王发麟， 廖文和， 郭 宇， 鞠传海

（南京航空航天大学机电学院，江苏 南京 210016）

复杂机电产品线缆信息本体表达与存储分析

王发麟， 廖文和， 郭 宇， 鞠传海

（南京航空航天大学机电学院，江苏 南京 210016）

针对复杂机电产品中线缆工程语义信息统一表达难、线缆复杂拓扑结构难以表示和存储的问题，提出基于本体和无向图的复杂线缆信息表达与存储分析方法。首先建立了基于布线设计、装配工艺规划和仿真分析3个维度的线缆信息集成模型；然后利用本体技术对模型信息进行了本体建模，增强了线缆语义信息的表达；最后利用一种水平分割算法将线缆零件划分成一个无向图，在此基础上建立邻接表，实现了线缆零件无向图在计算机中的存储和表达。通过将该方法应用到某线缆零件的实际分析中，验证了文中方法的可行性。

线缆；本体；无向图；信息集成模型；复杂机电产品

线缆作为传输能量和信号的介质，被大量应用于航空、航天、汽车、船舶等各类复杂机电产品中，是连接电子设备与各分机模块的“纽带”，线缆的优化布局和装配质量已成为衡量产品整机性能和可靠性的一个重要指标[1-2]。在工程应用中，线缆具有复杂的拓扑结构，涵盖了大量的几何拓扑信息、工程语义信息和分散的布线信息。工程语义信息的不一致性、线缆拓扑结构的复杂性以及线缆在计算机中的难以存储表示，是制约线缆虚拟布线设计与装配过程仿真的主要因素。对上述信息建立一个统一的信息集成模型，并对模型信息采用适当的方法进行工程语义表达，解决线缆拓扑结构的表示和存储问题，是实现线缆三维布线设计、装配工艺规划和仿真分析的基础，也是建立复杂机电产品数字化样机的信息基础。

为此，国内外一些学者围绕线缆拓扑结构的表示及信息模型的建立作了相关的研究。如 Conru[3]将线缆的布局问题分解为线缆拓扑结构的生成和线缆敷设两部分，并提出了以无向图的形式来表达线缆的拓扑结构，但因受限于当时的技术条件而并未实现；Hergenröther和Dahne[4]建立了用于虚拟环境中交互式布线设计中的线缆定长模型，同时提出将线缆束分为简单的线缆段以表达其整体结构，但是该文献没有对线缆信息的语义进行表达；魏发远等[5]建立了一个面向虚拟布线的电缆信息模型，该模型由电气模型、拓扑模型和几何模型等3个部分组成，但文中没有对线缆拓扑结构的建立及存储过程进行论述；万毕乐等[6]对导线、线束和导线单元等元素进行了定义，并建立了基于离散控制点的线缆模型，实现了对线缆主干、分支结构和导线信息的表达，但该模型对线缆结构的表达因导线的定义不同而不同，且在通用性、信息可拓展性等方面也受到较多的限制；王金芳等[7]根据线缆在复杂机电产品中存在方式和面向对象的建模思想分别建立了基线缆信息模型和线缆分支信息模型，体现了线缆信息的层次性，但也只限于信息的层次分类上，对信息语义并未处理；尚炜等[8]提出了一种以拓扑结构信息为骨架的线缆数字化模型，该模型虽然通过线缆基本元素间的包含关系和连接关系无向图建立了线缆的拓扑结构信息，但对于线缆拓扑结构图的建立过程并没有进行详细阐述；刘佳顺等[9]在分析线缆设计与制造流程的基础上，提出了一种虚拟环境下复杂线缆的集成信息模型，对不同类型的线缆信息进行了梳理，而对信息语义存在的冲突性和不一致性没有进行分析。

上述研究成果分别从线缆建模的不同方面进行了研究，但在线缆工程语义信息的不一致性和线缆拓扑结构表示及存储的解决方面还有待进一步研究。本文在前人研究的基础上提出基于本体和无向图的复杂线缆信息表达与存储分析方法。该方法首先从布线设计、装配工艺规划和仿真分析 3个维度建立线缆信息集成模型(cable harness information integrated model, ChIIM)；为增加线缆在布局设计和装配过程仿真及分析中的语义信息，利用本体技术对线缆信息进行本体建模；最后利用一种水平分割算法将线缆零件划分为一个无向图，通过建立无向图的邻接表来实现线缆零件无向图在计算机中的存储和表达。该方法能较好地解决工程实际中线缆语义信息统一表达难和线缆的存储问题，从而满足在布线设计、工艺规划和仿真分析中对线缆信息有效检索的要求。

1 线缆信息集成模型

在复杂机电产品设计中，线缆因其具有柔性特性而包含大量的信息，线缆信息的完整性和良好的语义表达是开展基于产品数字样机的线缆虚拟布线设计、线缆装配工艺规划和线缆装配过程仿真及分析的重要前提条件。本文遵从“产品设计→工艺规划→产品加工”的实际产品研制流程，从布线设计、装配工艺规划和仿真分析3个坐标维度建立了ChIIM，如图1所示。

ChIIM主要描述了线缆各种属性的相关信息，如线缆几何信息、线缆拓扑信息、线缆物理属性信息、电气功能信息、线缆材料信息、辅助材料信息等，每一类信息又包含更多表征线缆实际工作状态的信息内容。在含有柔性线缆的复杂机电产品系统的装配仿真过程中，布线设计决定了装配工艺，装配工艺是进行装配过程模拟的依据，而ChIIM的建立则是上述工作开展的基础和前提条件，是每一阶段所需的数据来源。

为保证极其复杂的产品设计在最短的设计周期内尽量达到性能最优，应尽可能地在产品的系统设计阶段即引入仿真分析，以帮助设计人员及早发现问题。相较于传统的将与线缆相关的信息进行罗列而生成的模型，基于布线设计、工艺规划和仿真分析3个维度而建立的ChIIM不仅将线缆的相关信息进行了集成表达，实现在布线设计-工艺规划、工艺规划-仿真分析、布线设计-仿真分析这3个层面进行信息的多次、循环调用，而且更能体现出3个不同研制阶段（布线设计、工艺规划和仿真分析）的内在关联性。

需要指出的是，在复杂机电产品的设计过程中，除了线缆信息作为数据来源外，刚性组件装配信息和电气组件信息也是必不可少的数据来源。因此，在上述ChIIM中对这两类信息进行了扩展，如电气组件信息包括组件的CAD模型、组件统一ID号、组件名、电气接口等；刚性组件装配信息包括各机械零部件、电气元器件间的相对位置和方向定位关系以及各机械零部件、电气元器件参与装配的局部几何结构之间的配合关系等。

图1 线缆信息集成模型

2 线缆信息本体建模

本体是共享概念模型的明确形式化规范说明[10]，是目前广泛接受的语义 Web知识表示方法，具有很强的语义表达能力，能够描述概念与概念之间的继承(is-a)关系、部分与整体(part-of)关系、概念实例与概念(instance-of)关系以及概念的属性(attribute-of)关系。本体确定了该领域内共同认可的概念明确定义，通过概念之间的关系描述了概念的语义，其任务是对某种形式化描述的近似，以建立一套计算机可以识别并理解的“机器描述”，从而使得人与人之间、人与机器之间以及机器与机器之间不但可以基于语法上而且可以基于语义上的交互。在针对复杂机电产品开展并行设计过程中，需要多次用到线缆相关信息，这些信息有的是本领域的知识，有的是其他领域的知识；有的是本地数据库、本地信息模型里的知识，有的是异地数据库、异地信息模型里的知识。这些不同存储源、不同层次的线缆设计信息之间由于其差异性导致的语义冲突和不一致，会造成设计过程中数据共享和数据重用困难等问题。因此，对于线缆信息所涉及的数据多、模型乱和系统异构等问题，本体技术可以通过建立统一模型对与线缆相关的信息进行组织，解决线缆工程语义信息的不一致，以最大限度实现数据共享，大幅提高线缆设计信息的使用效率。

基于 ChIIM的线缆信息本体建模可以从线缆类型和线缆信息分类2个大方面进行分析。“线缆类型”本体类描述了工程实际中常用的线缆表现形式，主要包括单芯导线、多芯线缆、扁平线缆以及线束等4类子本体。“线缆信息分类”本体类按照 ChIIM 的分类表示法，主要由线缆几何信息、线缆拓扑信息、线缆物理属性信息、线缆管理信息、线缆辅助材料信息等组成。每一个子本体类可以再细划分为子子本体，如“线缆几何信息”本体类可以细划分为线缆分支空间路径、线缆分支情况、分支空间位姿、分支截面形状、分支截面大小等；“分支截面形状”本体类又可以细划分为圆形、扇形等。“物理属性信息”本体类可以细划分为线缆密度、抗弯特性、抗拉特性、最小折弯半径等。“线缆管理属性信息”本体类可以细划分为线缆名称、线缆代号、技术要求、设计版本等。基于 ChIIM的线缆信息本体模型如图2所示。

图2 线缆信息本体模型（部分）

图2中“线缆标识”类用来唯一标识该线缆信息（规格型号等）；“信息描述”类主要帮助设计人员对线缆信息的理解；圆形、扇形和瓦形以实例形式附属于“分支截面形状”本体类。例如，在一项复杂机电产品设计任务中，设计人员被要求设计一根型号为BVV的铜芯聚氯乙烯绝缘氯乙烯护套圆形线缆，要求包括线缆类型为多芯线缆，芯线数为3根，截面形状为圆形，最小折弯半径为0.5 mm，单根导线直径为2.5 mm，护线套为绝缘胶带。设计信息的本体表达如下。

＜线缆设计信息 rdf:ID="多芯线缆的设计"＞

＜线缆标识 rdf:datatype="http://www.w3.org/2001/XMLSchema#string"＞spool标识365＜/线缆标识＞

＜信息描述 rdf:datatype="http://www.w3.org/2001/XMLSchema#string"＞

设计一根型号为BVV的铜芯聚氯乙烯绝缘氯乙烯护套圆形线缆

＜/信息描述＞

＜规格＞

＜线缆类型设计 rdf:ID="多芯线缆设计"＞

＜类型 rdf:datatype="http://www.w3.org/2001/XMLSchema#string"＞多芯＜/类型＞

＜/线缆类型设计＞

＜/规格＞

＜规格＞

＜电气参数设计 rdf:ID="多芯线缆电气参数设计"＞

＜芯线数 rdf:datatype="http://www.w3.org/2001/XMLSchema#int"＞3＜/芯线数＞

＜截面形状 rdf:datatype="http://www.w3.org/2001/XMLSchema#string"＞圆形＜/截面形状＞

＜单根导线直径 rdf:datatype="http://www.w3.org/2001/XMLSchema#float"＞2.5＜/单根导线直径＞

＜物理属性＞

＜最小折弯半径 rdf:datatype="http://www.w3.org/2001/XMLSchema# float"＞ 0.5 ＜/最小折弯半径＞

＜/物理属性＞

＜/规格＞

＜辅助材料＞

＜护线套 rdf:datatype="http://www.w3.org/2001/XMLSchema#string"＞绝缘胶带＜/护线套＞

＜/辅助材料＞

＜/线缆设计信息＞

3 线缆拓扑结构表示及存储

3.1 线缆图像划分及无向图建立

线缆拓扑结构中包含线缆图像特征最有效的数字化信息。为了表达线缆的拓扑结构，建立一个信息完整的线缆数字化模型，文献[3,8,11-12]进行了相关的研究，虽然对线缆无向图的建立及存储方法有所提及，但只停留在方法的表述上，具体的无向图建立过程没有作详细介绍和分析。

本文以图3中某三维线缆零件作为划分对象，采用文献[13-14]提出的划分算法对线缆图像进行划分，并在线缆划分结果的基础上建立线缆的无向图，用图论的思想[15]来表达线缆零件的拓扑结构。因篇幅有限，具体的划分步骤在此省略。

图3 某三维线缆零件

按照上述划分算法将图 3划分成图 4(b)中CabS1,CabS2,…,CabS9共9个线缆段部分(这里只考虑图4(b)中Ⅰ区域所示线缆零件)。

图4 线缆零件划分图像及无向图的建立

用无向图的顶点来表示线缆段的端点及线缆段与线缆段之间的连接点，用无向图的边（或弧）来表示端点与连接点（或连接点与连接点）之间的关系。如果线缆段连接点间是上下紧密相连的，则端点或连接点所对应的顶点之间存在边，否则就不存在。令G表示无向图，V表示顶点集，E表示边（或弧）集， vi表示顶点， ei表示边。利用上述无向图建立方法，对图4(a)、(b)建立的线缆无向图如图4(c)所示。为方便下文线缆无向图的存储分析，将图4(c)单独表示成如图5所示。其中边ei(·)括号内的数值代表该段线缆展平后的长度。

图5 线缆零件无向图

根据上述分析，有：线缆无向图G=(V,E)；顶点集V(G)={v1,v2,…,v10}；边集E(G)={e1,e2,…,e9},或E(G)={(v1,v2,8),(v1,v3,10),(v1,v4,6),(v1,v5,16), (v5,v6,20),(v6,v7,18),(v7,v8,15),(v8,v9,7),(v8,v10,9)}。上述边的集合E(G)中，每个元素的第3个分量表示该边的权值(长度值)。

3.2 线缆无向图的存储

关于图的存储表示方法有很多种，常用的有3种：邻接矩阵(adjacency matrix)、邻接表(adjacency list)和邻接多重表(adjacency multilists)。对图5中的线缆零件无向图分析可得无向图G的邻接矩阵为：

对()AG求平方，得：

首先对A2(G)进行分析。由A2(G)的主对角线上元素非零可知，每个顶点vi(i=1,2,…,10)都有长度（此处“长度”表示边的数量）为2的回路，其中顶点 v1有4条，分别为：v1v2v1、 v1v3v1、 v1v4v1和v1v5v1；顶点 v5、v6和 v7各有2条，分别为：v5v1v5和v5v6v5、v6v5v6和v6v7v6、v7v6v7和v7v8v7；顶点 v8有3条，分别为：v8v7v8、v8v9v8和v8v10v8；顶点 v2、v3、v4、v9和 v10只有1条，分别为：v2v1v2、v3v1v3、v4v1v4、v9v8v9和v10v8v10。分析每个顶点的回路数，有助于对图G的连通性和不同顶点所属的连通分支进行判断，进而判断线缆段之间的连接和分支情况。

记无向图的边数为N(E)，顶点数为n，易知N(E)=9，n=10，邻接矩阵A(G)中的元素个数为n×n=100。由于N(E)＜＜n×n，边的数目相对于A(G)中的元素个数比较少，邻接矩阵里存储了较多的无用信息，使用邻接矩阵存储会浪费较多的存储空间，而用邻接表存储则可以节省较多的存储空间。因此，本文采用邻接表的形式来存储线缆零件无向图。

(1) 建立顶点数组。顶点数组用来记录线缆零件无向图中各个顶点的信息。数组元素下标从0开始计起。对于图5中的线缆零件无向图，顶点集为V(G)={v1,v2,…,v10}，数组元素下标为0,1,…,9。据此建立的顶点数组如图6所示。

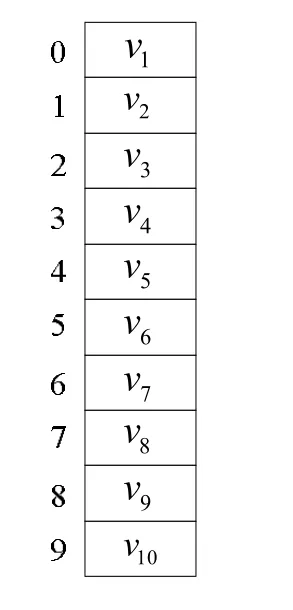
图6 线缆无向图的顶点数组

(2) 建立邻接表。在线缆无向图顶点数组的基础上，建立图5所示无向图对应的邻接表如图7所示。在邻接表的顶点数组中，每个元素有两个成员：一个成员用来存储顶点信息；另一个成员为该顶点的边链表的表头指针，指向该顶点的边链表。如果没有从某个顶点发出的边，则该顶点没有边链表，因此表头指针为空(用符号“∧”表示)。此外，为了在邻接表中将边的权值也进行存储，在边结点中增加了一个存储单元，如边结点中的中间数值“8”即代表边的权值。

(3) 线缆无向图最短路径搜索。最短路径问题要解决的就是求加权图G=(V,E,W)(W表示边ei上的权值)中两个给定顶点之间的最短路径。为实现对线缆拓扑结构中某些特定信息的查询，如任意两顶点间的最短路径搜索、通路搜索等，可利用Floyd-Warshall算法[16]求得。Floyd-Warshall算法用于求解任意两点间的最短距离，算法通过考虑最佳子路径来得到最佳路径，其时间复杂度为O(n3)(n为顶点数)。

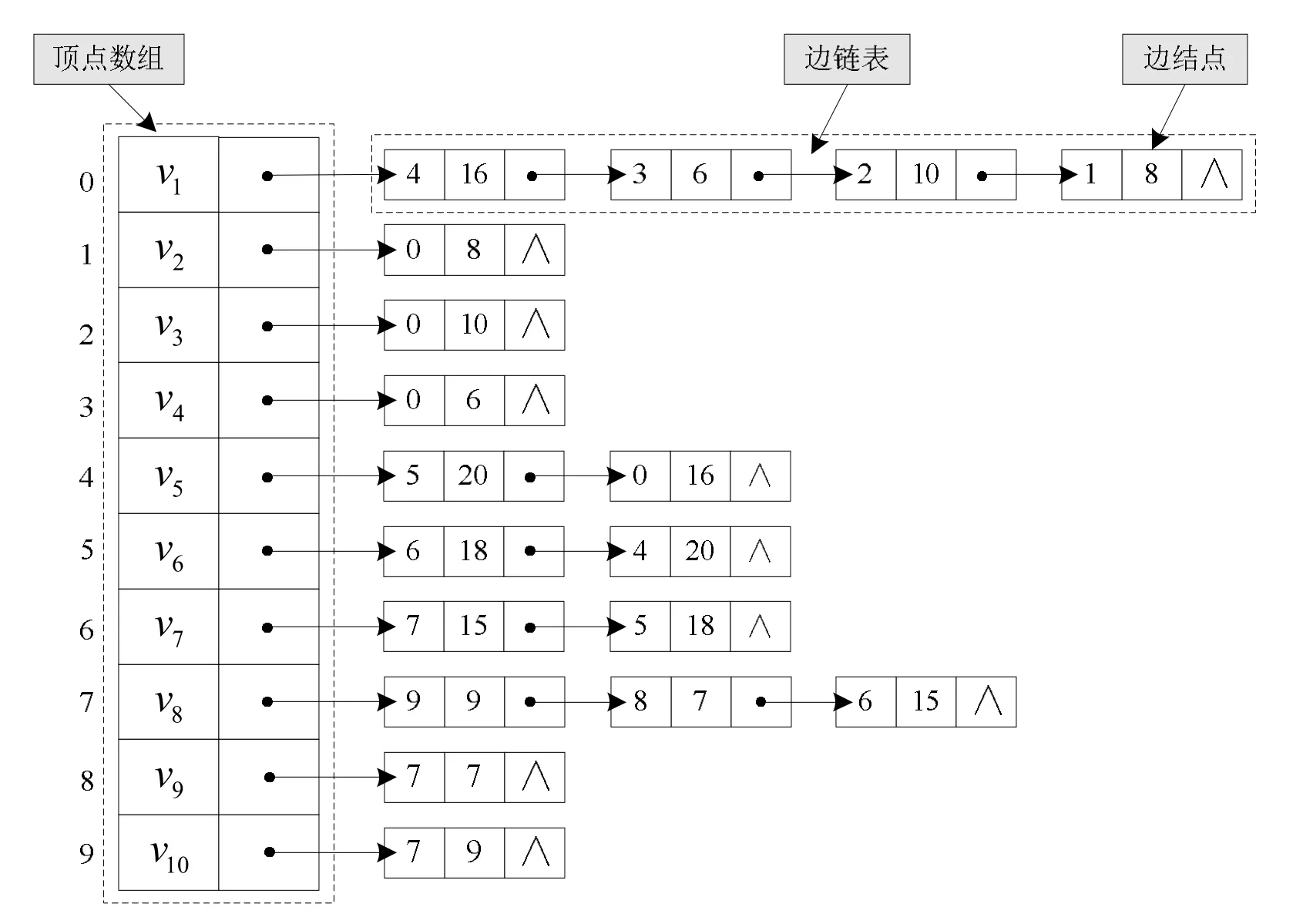
图7 线缆无向图的邻接表

4 方法验证

利用Visual C++6.0开发环境，在邻接表存储算法基础上，分别输入线缆零件无向图中的顶点数：10；边数：9；所有顶点下标：0，1，…，9；每条边所连接的顶点对：(0, 1)、(0, 2)、(0, 3)、(0, 4)、(4, 5)、(5, 6)、(6, 7)、(7, 8)、(7, 9)。运算结果如图8所示。通过比较图8的运算结果和本文所建立的线缆无向图的邻接表(图 7)可知，两者的结果一致，表明本文建立的无向图邻接表可以有效地对线缆无向图进行存储。需要说明的是，权值的存储在这里不作考虑。

图8 线缆无向图邻接表的存储实现

为求解线缆拓扑结构中任意两顶点间的最短路径值，由图5可得线缆无向图G的权值矩阵为：

其中，元素wij(1≤i,j≤10)表示边vivj上的权值。若顶点 vi与顶点vj无连边，则 wij=∞。据此利用Floyd-Warshall算法可求出某一固定顶点到各个顶点之间的最短距离值。本文中将顶点 v6设置为固定点，从而求得顶点v6到其他各个顶点(v1,v2,…,v10)之间的最短距离值分别为：36、44、46、42、20、0、18、33、40、42，其中值为“0”的数表示顶点 v6到自身的距离。同时求得各条路径所经过的顶点分别为：v6→v5→v1→v1（对应最短距离值36）、v6→v5→v1→v2（对应最短距离值44）、v6→v5→v1→v3（对应最短距离值46）、v6→v5→v1→v4（对应最短距离值42）、v6→v5→v5（对应最短距离值20）、 v6（对应最短距离值0）、v6→v7（对应最短距离值18）、v6→v7→v8（对应最短距离值33）、v6→v7→v8→v9（对应最短距离值40）、v6→v7→v8→v10（对应最短距离值 42）。重复的顶点视为一个顶点。

5 结 束 语

线缆因具有复杂的拓扑结构和几何形态、繁杂的工程语义信息而使得线缆的信息建模成为顺利开展布线设计、装配工艺规划和仿真分析的一个重要前提。本文提出了一种基于本体和无向图的复杂线缆信息表达与分析方法，该方法从布线设计、装配工艺规划和仿真分析 3个维度建立ChIIM，从本体建模技术的角度分析并建立了线缆的工程语义信息本体模型，通过建立邻接表来实现线缆零件无向图在计算机中的存储和表达。该方法能较好地解决工程实际中线缆语义信息统一表达难和线缆的存储问题。

[1] 宁汝新, 刘检华, 唐承统, 等. 虚拟装配技术及其应用[J]. 国防制造技术, 2009, 4(2): 22-29.

[2] 尚 炜, 宁汝新, 刘检华, 等. 复杂机电产品中的柔性线缆装配过程仿真技术[J]. 计算机辅助设计与图形学学报, 2012, 24(6): 822-831.

[3] Conru A B. A genetic approach to the cable harness routing problem [C]//Proceedings of the 1st IEEE Conference on Computational Intelligence. Washington, D. C., USA, 1994: 200-205.

[4] Hergenröther E, Dahne P. Real-time virtual cables based on kinematics simulation [C]//Proceedings of the WSCG 2000. Pilzěn, Czech Republic: University of West Bohemia, 2000: 402-409.

[5] 魏发远, 陈新发, 王峰军. 电缆虚拟布线及其逆运动学仿真[J]. 计算机辅助设计与图形学学报, 2006, 18(10): 1623-1627.

[6] 万毕乐, 宁汝新, 刘检华, 等. 虚拟环境中线缆建模及布线的研究与实现[J]. 中国机械工程, 2006, 17(20): 2135-2139.

[7] 王金芳, 闫 静, 武 凯, 等. 基于Pro/E的线缆装配工艺规划系统关键技术研究[J]. 中国机械工程, 2008, 19(13): 1565-1569.

[8] 尚 炜, 宁汝新, 刘检华, 等. 一种以拓扑结构信息为骨架的线缆数字化模型[J]. 计算机集成制造系统, 2012, 18(12): 2588-2594.

[9] 刘佳顺, 刘检华, 王志斌, 等. 虚拟环境下复杂线缆的集成信息模型[J]. 计算机集成制造系统, 2013, 19(5): 964-971.

[10] Studer R, Benjamins V R, Fensel D. Knowledge engineering: principles and methods [J]. Data & Knowledge Engineering, 1998, 25(1-2): 161-197.

[11] Parmantier J P, Junqua I, Bertuol S, et al. Simplification method for the assessment of the EM response of a complex cable harness [C]//Proceedings of the 20th Int. Zurich Symposium on EMC, Zurich, 2009: 161-164.

[12] Ridel M, Savi P, Alberti M, et al. Numerical simulation of aeronautic cable topology and experimental validation [C]//Proceedings of the 2011 International Conference on Electromagnetics in Advanced Applications (ICEAA), Torino, Italy, 2011: 1356-1359.

[13] 杨承磊, 孟祥旭. 一种新的快速细化算法的设计与实现[J]. 工程图学学报, 1998, 19(3): 87-93.

[14] 杨承磊, 孟祥旭, 李学庆, 等. 基于无向图的图像整体骨架表示模型及其算法[J]. 计算机学报, 2000, 23(3): 293-299.

[15] 蒋建国, 张 婕, 詹 曙, 等. 层次式图切分快速分割算法[J]. 图学学报, 2012, 33(1): 44-49.

[16] 王海英, 黄 强, 李传涛, 等. 图论算法及其MATLAB实现 [M]. 北京: 北京航空航天大学出版社, 2010: 154.

Stored Analysis and Ontology Expression of Cable Harness Information for Complex Mechatronic Products

Wang Falin, Liao Wenhe, Guo Yu, Ju Chuanhai

(College of Mechanical and Electrical Engineering, Nanjing University of Aeronautics and Astronautics, Nanjing Jiangsu 210016, China)

It was difficult to afford unified expression and storage for semantic information and complex topological structure of the cable harness in complex mechatronic products. Aiming at this problem, a method of expression and stored analysis on complex cable harness information based on ontology and undirected graph was proposed. A cable harness information integrated model based on three-dimensional degrees of wiring design, assembly process planning and simulation analysis was established firstly. Then the expression of cable harness semantic information was enhanced through the ontology modeling of the model information by using the ontology technology. Finally, divide the cable harness part into an undirected graph by using a horizontal split algorithm. On this basis, an adjacency list of undirected graph was built, and the storage and expression of the cable harness undirected graph in the computer were realized. A certain cable harness part was taken as the application case to verify the feasibility of this method.

cable harness; ontology; undirected graph; information integrated model; complex mechatronic products

TP 391

A

2095-302X(2015)03-0376-08

2014-09-14；定稿日期：2014-12-10

国防基础科研资助项目；江苏省研究生培养创新工程资助项目(KYLX_0311)；中央高校基本科研业务费专项资金资助项目

王发麟(1986-)，男，江西吉安人，博士研究生。主要研究方向为数字化制造技术、虚拟装配。E-mail：wj54nh@sina.com