结合广义重心坐标与Voronoi剖分的函数分片逼近

肖艳阳， 涂锦灿， 陈中贵

（1. 厦门大学福建省智慧城市感知与计算重点实验室，福建 厦门 361005；2. 厦门大学计算机科学系，福建 厦门 361005）

结合广义重心坐标与Voronoi剖分的函数分片逼近

肖艳阳1,2， 涂锦灿1,2， 陈中贵1,2

（1. 厦门大学福建省智慧城市感知与计算重点实验室，福建 厦门 361005；2. 厦门大学计算机科学系，福建 厦门 361005）

结合广义重心坐标理论，提出了一个新方法，以解决在平面区域上的函数逼近问题。该方法通过构建基于广义重心坐标的最优分片函数来逼近目标函数。采用Voronoi图来划分区域，并提出一个度量逼近误差的能量函数。推导出该函数的导数后，采用一种高效的Voronoi节点更新方法来获得区域的最优剖分，并通过最优剖分构建最优分片函数。由于该方法对不连续函数具有良好地逼近能力，因此将其应用在图像逼近问题中。分别在解析函数和彩色图像上对该方法进行实验，均获得了很好的逼近效果。

广义重心坐标；函数逼近；Voronoi图；图像逼近

函数逼近问题是指任意给定一个目标函数，在该函数的定义域上，构造一个新的函数，使得新函数与目标函数尽可能一致。两个函数之间不一致的程度可用逼近误差来度量，误差越小，两个函数越接近。如果在目标函数的定义域上只构建一个函数来逼近它，误差可能会较大。一般的想法总是在误差最大的区域上细分成多个区域。但是这会造成过多的子域，如何减少剖分的数量也是一类值得研究的问题[1]。这种将定义域划分成多个子域，再在每个子域上分别构建一个新函数来逼近目标函数的方法即分片的函数逼近，它是研究逼近问题的重要方法。

对于分片逼近来说，基于多项式的简易性和灵活性特点[2]，Chen等[3]提出了一种在Voronoi剖分上构建最优分片多项式的方法。分片多项式需要同时考虑多项式的阶次和对区域的剖分，一旦指定了阶次和剖分的数量，分片多项式的逼近问题就转化成如何划分区域。因为得到剖分之后，每个子域上的多项式就可以通过求解线性最小二乘问题得到。因此，对区域良好地剖分是分片逼近问题的关键。

受此启发，本文提出一种新的分片逼近方法，即结合广义重心坐标和Voronoi剖分，通过构造最优分片函数来逼近二维定义域上的目标函数，其中，逼近误差采用常用的 L2范数来衡量。因此本文方法只需要考虑如何获得区域的最优剖分。划分区域有许多方法，如三角剖分，本文采用Voronoi图，它是由Voronoi节点集合唯一决定的结构。在形成的剖分中，每一个Voronoi多边形都对应一个逼近函数，而由于节点集合唯一决定了Voronoi图的形成，因此逼近误差间接取决于节点集合的分布。把逼近误差极小化对应的剖分称为最优剖分，此时的点集分布为最优分布，该剖分对应的分片逼近函数称为最优分片函数。

在此基础上，本文提出了一个新的能量函数来衡量逼近误差，并推导出相应的梯度。然后采用一种高效的节点优化方法来更新节点位置，使得能量函数值极小化，从而获得最优剖分和最优分片函数。为了验证方法的有效性，分别在连续的和不连续的解析函数上应用该方法，均能获得很好地逼近效果。由于该方法对不连续函数有很强地逼近能力，而图像可以看作是不连续的函数，所以将该方法应用到图像逼近领域。实验结果表明，该方法对彩色图像也能产生较好的结果。

1 相关研究和背景

1.1 相关研究

分片函数逼近。Powell[2]详细介绍了函数逼近的概念和基本方法。分片逼近是该领域的一种重要方法，其中，分片多项式的方法已经有较多的研究成果[1-8]。大多数相关研究是针对单变量函数的逼近问题，而多变量的多项式逼近问题则更加复杂。如果多项式的基函数是正交的，Fedele和Ferrise[4]的方法可以用来处理最小二乘逼近问题。单变量的正交多项式可以使用 Gram-Schmidt过程来构建，而多变量的情况则面临诸多数学和算法上的困难。然而在一些特殊区域中已经可以构造二变量的正交多项式，如Dunkl[5]的正六边形区域和Farouki等[6]的三角形区域。在任意区域中构建多变量正交多项式的问题仍然值得研究。Lecot和 Lévy[7]则使用幂基多项式构建二变量的逼近函数，区域的剖分是根据底层函数值进行聚类得到的。Chen等[3]的方法中也使用了幂基多项式，但是采用了更为简单的Voronoi图作为区域的剖分结构，通过获取最优剖分得到最优逼近多项式。Nivoliers和Lévy[8]的方法在平面区域上即可看做Chen等[3]方法的特殊情况，即多项式取常数值。本文与Chen等[3]的方法类似，但是可使用几何意义更鲜明的重心坐标来构造分片函数，并获得了很好的效果，而且数值计算更加稳定。

图像逼近。该领域已经有很多研究成果和高效的算法被提出来[3,7-14]。许多方法是通过自动提取图像特征的几何信息实现的，如通过边缘检测算法提取图像的特征曲线，再根据特征线构建矢量曲线和像素簇。比较常见的用几何信息来表达图像的方法，如 数据 相关 的三 角化 (data-dependent triangulation, DDT)，通过构建图像的三角剖分，再线性插值出像素的颜色值。Dyn等[9]结合三角剖分的顶点位置分布和对应的值进行三角剖分的构建，同时讨论了不同的定义准则的优、缺点。Li和Adams[10]在此基础上提出了一种用来表达图像的三角网格生成框架，根据不同的规则，该方法不断地向网格中误差最大的三角片上添加顶点，从而逐渐细分网格。DDT方法的另一个方向是通过简化复杂网格并在达到最大误差时结束，如 Yin等[11]的方法中使用了网格简化。Su和Willis[12]则提出了像素级别的DDT方法，可将低分辨率的图像放大到更高分辨率。但是大多数方法都不能显式地表达出图像的不连续特点，为了捕捉到图像的特征线，DDT方法只能在特征线两边放置大量的点。Tu和Adams[13]的方法则根据图像不连续特征，提出了一种新的网格模型生成方法。首先提取图像的特征线，根据特征线定义约束的Delaunay边并产生初始网格，然后再不断地向网格误差大的片上添加顶点。Kreylos和Hamann[14]则应用模拟退火的方法优化网格顶点位置来获取最优三角剖分，继而得出拟合图像。Lecot和Lévy[7]将Cohen-Steiner等[15]的框架扩展到图像处理中，从而提出了一种新方法，可以将光栅图像矢量化。该方法将图像划分成多个不规则的子区域，每个区域的边界用矢量曲线来表达，内部由事先构造的三角像素组成，再根据能量函数的梯度更新子区域。Yin等[11]结合一种新的二次误差度量(quadric error metrics)，提出了将光栅图像参数化的新方法，并将其应用在图像重建中。Chen等[3]的方法则通过获取图像的最优剖分，再从该剖分中构建最优多项式的方法重建图像。类似地，将本文方法应用在图像逼近中则通过构建基于广义重心坐标的最优分片函数来拟合原图像，能获得很好的效果。李海洋等[16]应用 K-均值聚类的方法产生了类似于文献[7]中的图像分割效果，它们的剖分都是不规则的，本文方法应用在图像上的剖分在一定程度上也可看做一种分割结果。

1.2 背景知识

Voronoi图是计算几何中重要的基础概念，在计算机图形学、图像处理、地理信息系统和生命科学领域都有广泛地应用[17]。假设在二维紧致区域Ω⊆R2中，有N个位置互异的节点组成的集合则在欧式距离度量下，节点xi对应的Voronoi区域为：

本文方法基于广义重心坐标，其包括均值坐标(mean value coordinates, MVC)[18]、调和坐标(harmonic coordinates, HC)[19]、格林坐标(Green coordinates, GC)[20]和Wachspress坐标[21]。MVC将多边形内的任意点表达为多边形各个顶点的线性组合，因此在多边形内部具有良好的光滑性，在顶点处则是C0连续。假设在一个任意的平面多边形中，各个顶点表示为｛p1,p2,…,pmi｝，mi表示该多边形的顶点个数，则在多边形内的任意一点可以表示成：

其中，Ck≥0,k=1,…,mi，Ck（q）代表点q在该多边形中相对顶点pk的重心坐标值（权值）。

图 1是均值重心坐标的示例图。在该多边形中，内部的任意点相对多边形的每个顶点都有一个权值C。权值越大，代表顶点对其影响越大。以图1为例，该多边形有6个顶点，其中左上的子图代表多边形内部的点对于顶点1的权值分布，中上的子图代表多边形内部的点对于顶点 2的权值分布，以此类推。

Wachspress坐标[21]最先用于有限元计算，在平面中，它的计算可采用Meyer等[22]的方法，但是计算结果可能会产生极点，在非凸的多边形中会产生负值坐标。因此Wachspress坐标适用于单个凸多边形。而MVC由于在整个平面上具有良好地闭形式定义，因此适用于不自交的任意多边形以及多边形的嵌套[18]。与MVC不同，HC的定义并不是闭形式，但是在多边形内部它也是非负的，并且在整个平面没有极点，因此HC能够很好地保持以往重心坐标的性质[19]。Lipman等[20]结合格林第三定理提出了用于变形的GC，它在计算中考虑了多边形边界的法向量，因此变形过程可以保持细节特征。

图1 多边形内的点相对各个顶点的权值分布

2 基于广义重心坐标的分片函数逼近

2.1 能量函数的定义

设函数f（x）是定义在二维紧致区域Ω中的函数。在该区域上有Voronoi剖分取定函数空间Φ，基函数取为广义重心坐标基。根据广义重心坐标理论，在任意一个 Voronoi多边形区域内都可以构建一个定义在Φ中的函数其中λk,k=1,…,mi表示多边形的顶点pk在该函数中的取值，其余符号的意义同重心坐标部分。λk具有良好的几何意义，即在该平面多边形中，顶点pk的高度值，k=1,…,mi。

于是在每个子区域Ωi中，f（x）都可以用一个新函数Hi（x）来逼近。建立一个衡量逼近误差的函数，即每个子域上误差的累加和，表达为：

将该函数称为本文的能量函数。将目标转化成求解该函数的极小值，以获得逼近f（x）的最优分片函数。

对能量函数来说，最优的概念包含两部分：对区域Ω的剖分最优和在每个子域Ωi上对应的函数最优。当剖分确定时，子域Ωi上对应的最优函数满足下式：

在子域Ωi上的逼近误差：

分别对λk,k=1,…,mi求偏导，并令其为0，得：

整理得：

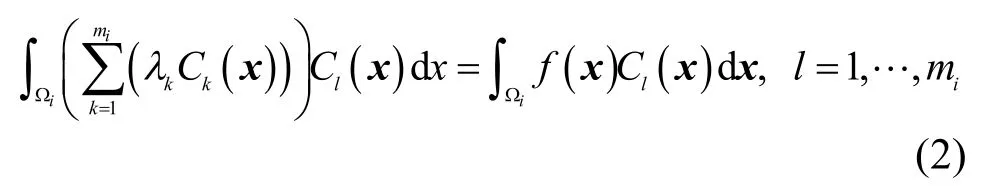
因此Ωi上的最优函数仅依赖于剖分。而唯一决定Voronoi剖分的就是节点的位置，所以可以将节点集合看做唯一变量，重写能量函数为：

下面探讨如何找到点集X的最优位置分布。现有的许多优化方法，如梯度下降法、共轭梯度法等，都是基于梯度信息。因此，先推导出能量函数的梯度。

2.2 E（X）梯度的计算

用 Ji表示与Ωi相邻的Voronoi多边形对应的节点的序号集合。为了推导E（X）对节点xi的导数，只需要考虑在E（X）中与xi相关的项。因此，能量函数对 xi求偏导：

注意到xi出现在被积函数和积分区域当中，需考虑积分区域中变量的不同情况。

首先，应用Leibniz规则[23]来简化这个公式。假设Dt是一个在时间t上光滑连续的二维区域，g（x,t）,x∈Dt是定义在Dt上的一个函数。将一个在区域边界∂Dt上的点的速度矢量表示为v=∂x∂t，用n代表该边界上指向外的单位法向量。一般的Leibniz规则[23]是：

其中，ds是在封闭的边界曲线tD∂上的弧长单元。因此，在式(4)中应用Leibniz规则，得到：

其中，Ωij=∂Ωi∩∂Ωj，是Ωi与Ωj的公共边。

式(5)右边的第一项，根据包络定理[24]可以得到：

则等式两边对xi求偏导，得到：

因此，得到：

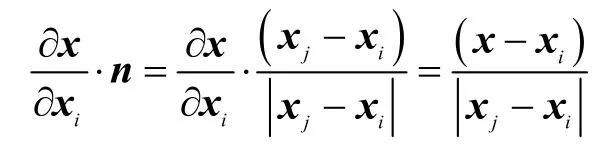
式(6)即为能量函数关于Voronoi节点的导数公式。计算得到函数的梯度之后，采用一种新颖的基于梯度信息的优化方法来优化点集X的分布。

2.3 优化算法

Nivoliers和Lévy[8]介绍了一种新的基于梯度的优化算法，Chen等[3]则从自适应的角度对迭代步长作了改进。这里引述文献[3]中的算法过程。从初始位置开始，节点的位置根据下式进行迭代更新，

i迭代时的步长。需要特别说明的是，在这个优化式子中，由于下降方向是通过将各自梯度分量除模得到的，所以不再是梯度的方向，该优化过程也不是梯度下降法。每一次迭代的步长由下式控制：

其中，maxJ是指定的最大迭代次数，是节点xi的初始步长。其中k是缩放参数，Ωi是节点 xi对应的Voronoi多边形区域。

这种方法比经典的优化算法，如传统的梯度下降法、共轭梯度法和L-BFGS法，更加高效，能够优化经典算法无法优化的情况。基于此，提出本文算法如下：

算法1. 基于重心坐标的分片函数逼近

输入. 函数f（x），初始点集X，最大迭代次数Jmax

输出. 点集X的最优Voronoi剖分和对应的最优函数集合

(1) 计算点集X的Voronoi剖分

(2) 计算点集的初始步长

(3)DO

计算当前点集X的Voronoi剖分和对应的最优分片函数

计算能量函数的梯度

根据优化方法更新点的位置，仍记为X

WHILE迭代次数小于Jmax

(4) 计算结果点集X的Voronoi剖分和对应的最优分片函数

由于本文中能量函数的连续性不高，特别是对于不连续的图像来说，更达不到 C2连续。梯度下降法、共轭梯度法和L-BFGS方法等传统的优化算法，无法彻底地优化能量函数。在实验中，传统的优化算法运行了几次迭代之后就停止了，Voronoi剖分并没有得到较好地优化。本文采用的优化算法将变量的梯度信息除模，为其指定了优化方向，但该方向已不再是梯度下降的方向。因此给定合适的步长之后，该算法可以强制更新Voronoi节点的位置，直到达到指定的迭代次数。

对于算法中的初始化，本文采用简单的随机算法。在产生随机节点时，抛弃重合的点，以保证剖分个数为指定的数量。

将该算法应用在图像逼近问题时，把图像作为底层函数，将像素颜色值正规化。先产生初始剖分，根据算法流程，在达到最大迭代次数时，得到最优剖分。据此，在每个分片上计算最优逼近函数。根据这个函数，对位于该分片内的像素重新计算颜色值。新的颜色值可能会越界（大于255或小于0），因此将其截断在0～255范围内，即大于255的值设为255，小于0的值设为0。再把计算得到的颜色值填充到该像素中。重复该过程即可得到拟合图像。拟合图像与原图像的相似程度可以用峰值信噪比(peak signal to noise ratio, PSNR)来衡量。理论上，PSNR值越高，两幅图相似程度越大。

3 实验结果

本文算法使用了C++编程语言。所有的实验都是在Intel I5 3.1 GHz CPU和4.0 GB内存的PC机进行的。其中，使用计算几何(computational geometry algorithms library, CGAL)算法库[25]来计算 Voronoi剖分。

采用文献[26]的程序来计算重心坐标。另外由于本文算法需要计算很多的积分，为了提高效率，对于一般的解析函数积分，使用 Dunavant积分规则[26]来简化计算。具体的做法是，对每个 Voronoi多边形，将其划分成三角形剖分，每个三角形由多边形中心与多边形每条边的两个顶点连接而成。然后在每个三角形中利用Dunavant规则[27]计算积分。而对于图像上的积分，不再使用普通的正方形像素，而是将每个多边形划分成三角像素的集合，每个三角像素的面积约为原像素面积的2倍。对于梯度的计算，边界积分使用经典的两点高斯积分规则（连续函数）和一点高斯积分规则（图像）。

图2和图3是本文算法对一般解析函数的剖分图。图2所示为算法对连续函数：

的剖分结果。该函数在x+y=0处是C0连续的，从图中可以看到，Voronoi剖分的分布具有规律性，虽然函数是连续的，但在x+y=0处函数值变化较大，剖分很敏锐地捕捉到了这一特点。其他地方基本上沿着函数的梯度方向分布。

图3所示则是算法对不连续函数：

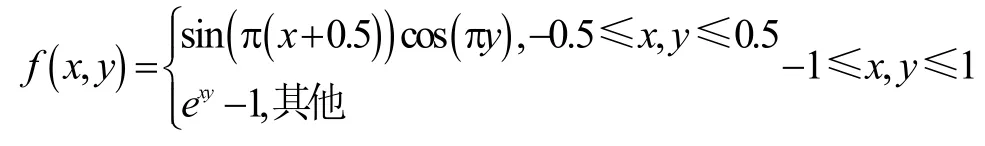
的剖分结果。分析结果可知，Voronoi剖分在函数的断层处可捕捉到函数的不连续特征。图中由Voronoi区域边界形成的近似正方形的内外区域分别对应函数的不同定义域的表达。

图2 本文算法逼近连续函数的结果

图3 本文算法逼近不连续函数的结果

在图像逼近中，普通的灰度图像可视为一个不连续的函数，由于本文方法具有很强地逼近不连续函数的能力（图3），所以将本文算法直接应用在灰度图像上是可行的，实验结果也证明了这一点。再做一些扩展，对于一幅RGB的彩色图像，将红、绿和蓝色通道分离出来，视为3个不连续的函数，r（x），g（x）和b（x）。为了在图像中同时逼近这 3个函数，把能量函数修改为：

其中，R*（x），G*（x）和B*（x）分别是对函数 r（x），g（x）和b（x）的最优函数。这个能量函数的导数推导过程与2.2节类似，算法1仍然可以执行。图4是本文算法的流程，图5～8是算法的结果，所有列出的PSNR值均为拟合图像与原图像的PSNR。

图4采用简单的随机算法初始化500个Voronoi节点，如图4(b)所示。通过不断地迭代更新节点位置，使得能量函数值逐渐减小，Voronoi剖分趋于最优。实验结果表明，绝大部分的Voronoi区域的边界都能够与图像的特征线重合，因此能够很好地拟合出原图像。图 4(b)～(d)的底层图像都是利用剖分对应的逼近函数重新拟合出来的。

本文方法可看做是文献[3]类型方法的扩充。一般的Voronoi多边形的顶点个数在5～7之间，以自由度来看，本文方法与文献[3]中的二次逼近（6个自由度）相近。图5是一个比较结果，从PSNR的角度看，本文方法与二次逼近方法得到的效果相近，而比线性逼近效果更好。而且，本文所使用的基函数具有更直观的几何意义，在数值计算方面也更加稳定。这主要体现在以下两方面：①本文算法和 Chen等[3]的算法，在求解最优逼近函数的过程中，都需要解一个线性方程组。Chen等[3]利用幂基多项式构建逼近函数，在求解该过程中的线性方程组时，有可能出现退化情况（即该方程组的秩小于方程的数量），如二次退化成线性的情况。而本文方法并不会出现这种退化情况。②Chen等[3]的算法中，多项式的阶次越高，求解最优多项式的线性方程组的系数矩阵越庞大，计算的复杂程度越大。而本文算法在该过程中的系数矩阵只跟Voronoi多边形的顶点个数相关。

本文方法还对算法内部的参数，即剖分数量和不同类型的重心坐标做了比较。图6分别是500、1 000和2 000个剖分执行算法后生成的拟合图，从图6(a)～(c)的PSNR值变化可知，逼近误差与剖分数量呈反比。但是过多的分片不利于算法效率，需平衡选择。图7所示为在相同的初始剖分下，分别使用均值坐标和Wachspress坐标执行算法的结果，对应的部分最优剖分分别显示在图像的下半部分。可以看到，使用不同的坐标产生的最优剖分虽然不同，但是均能产生良好地逼近效果。在实验中，由于多边形都是凸的，不需要考虑坐标值为负的情况，因此除了计算方式不一样外，算法的其他部分不需要做任何修改。算法的更多结果见图8。

图4 本文算法的流程图

图5 本文方法与文献[3]方法的比较

图6 不同剖分数量对结果的影响

图7 相同的初始化

图8 本文算法实验结果

表1是算法的运行时间统计。图像分辨率、剖分数量和计算梯度的精度都会影响算法中积分的计算，从而影响算法的效率。最大迭代次数也是影响算法运行时间的重要参数。将本文算法归结为以下四部分：构建三角像素、求解最优逼近函数、计算梯度和更新节点。分别对其进行时间统计，得到本文算法主要耗时在于构建三角像素和求解最优逼近函数。

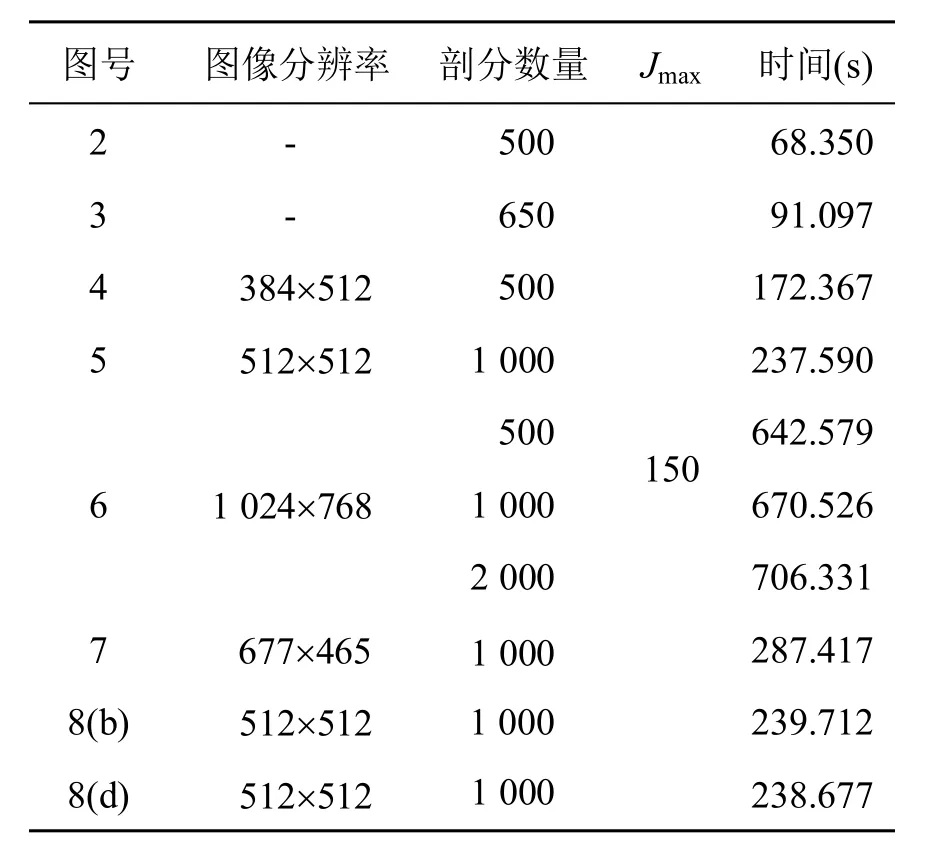
表1 运行时间统计

由于最优逼近函数求解出来之后，梯度的计算只涉及到线积分，而且相关参数也已经求解得到，因此计算量较小，耗时较少。重心坐标的计算贯穿于整个算法过程，在实验中，对于512×512的灰度图像，在多边形顶点个数均为6的情况下，本文算法对所有像素执行一次重心坐标的计算耗时为0.185 s。然而有些像素可能需要多次计算重心坐标，如某个像素同时出现在求解最优函数过程中和计算梯度过程中。另外需要注意的是，对于RGB图像来说，不同通道是分别计算的，重心坐标的计算量为灰度图像的3倍，因此算法运行时间更久。总体来说本文算法计算量较大，相比于Chen等[3]的算法，本文算法的运行速度也较慢。

4 结 束 语

本文提出了一种基于重心坐标的分片函数逼近方法。在广义重心坐标和Voronoi剖分的基础上，首先给出了衡量逼近质量的能量函数，该能量函数仅依赖于Voronoi节点的位置。 推导出该函数的导数后，采用文献[3]中改进的基于梯度的优化方法来优化节点位置，从而获取最优剖分和最优分片函数。实验结果表明，该方法对解析函数非常有效，并且能够应用在图像逼近问题上。关于与其他方法的比较，在相同自由度下，本文结果与其相近甚至更好，而且文献[3]中使用的基函数，其几何意义不明显，因此使用重心坐标更加合理。

不足之处在于，本文方法的逼近能力有限，当多项式阶次取更高时，Chen等[3]方法的逼近能力远远高于本文方法。而且，本文算法的运行时间相对更久（表1），对于某些应用可能是不可接受的。该算法与许多因素相关，主要耗时在于构建三角像素和梯度的计算。以后需考虑采用并行算法或图形处理器(graphic processing unit, GPU)执行来加速本算法。研究本文方法在不同基函数下的实现和内在联系，或者将其拓展到高维空间中，获取高维的最优剖分，或者应用在视频相关领域中，都是本文方法的后续工作。

[1] Prentice J S C. Range and domain partitioning in piecewise polynomial approximation [J]. Studies in Mathematical Sciences, 2011, 2(2): 67-77.

[2] Powell M J D. Approximation theory and methods [M]. Cambridge: Cambridge University Press, 1981: 25-30.

[3] Chen Zhonggui, Xiao Yanyang, Cao Juan.Approximation by piecewise polynomials on Voronoi tessellation [J]. Graphical Models, 2014, 76(5): 522-531.

[4] Fedele G, Ferrise A. Explicit solution of the finite time L2-norm polynomial approximation problem [J]. Applied Mathenatics and Computation, 2011, 217(21): 8354-8359.

[5] Dunkl C F. Orthogonal polynomials on the hexagon [J]. SIAM J. Applied Mathenatics, 1987, 47(2): 343-351.

[6] Farouki R T, Goodman T N T, Sauer T. Construction of orthogonal bases for polynomials in bernstein form on triangular and simplex domains [J]. Computer Aided Geometric Design, 2003, 20(4): 209-230.

[7] Lecot G, Lévy B. Ardeco: Automatic region detection and conversion [C]//Proceedings of the 17th Eurographics Conference on Rendering Techniques. Nicosia, Cyprus: Eurographics Association, 2006: 349-360.

[8] Nivoliers V, Lévy B. Approximating functions on a mesh with restricted Voronoi diagrams [J]. Computer Graphics Forum, 2013, 32(5): 83-92.

[9] Dyn N, Levin D, Rippa S. Data dependent triangulations for piecewise linear interpolation [J]. IMA Journal of Numerical Analysis, 1990, 10(1): 137-154.

[10] Li Ping, Adams M D. A tuned mesh-generation strategy for image representation using data-dependent triangulation [J]. IEEE Transactions on Image Processing, 2013, 22(5): 2004-2018.

[11] Yin Xuetao, Femiani J, Wongka P, et al. A new QEM for parametrization of raster images [J]. Computer Graphics Forum, 2011, 30(8): 2440-2451.

[12] Su Dan, Willis P. Image interpolation by pixel-level data-dependent triangulation [J]. Computer Graphics Forum, 2004, 23(3): 189-201.

[13] Tu Xi, Adams M D. Improved mesh models of images through the explicit representation of discontinuities [J]. IEEE Canadian Journal of Electrical and Computer Engineering, 2013, 36(2): 78-86.

[14] Kreylos O, Hamann B. On simulated annealing and the construction of linear spline approximations for scattered data [J]. IEEE Transactions on Visualization and Computer Graphics, 2001, 7(1): 17-31.

[15] Cohen-Steiner D, Alliez P, Desbrun M. Variational shape approximation [J]. ACM Transactions on Graphics (TOG), 2004, 23(3): 905-914.

[16] 李海洋, 文永革, 何红洲, 等. 基于随机权重粒子群和K-均值聚类的图像分割[J]. 图学学报, 2014, 35(5): 755-761.

[16] Okabe A, Boots B, Sugihara K. Spatial tessellations: concepts and applications of Voronoi diagrams [M]. New York: Wiley, 1992: 1-3.

[17] Hormann K, Floater M. Mean value coordinates for arbitrary planar polygons [J]. ACM Transactions on Graphics (TOG), 2006, 25(4): 1424-1441.

[18] DeRose T, Meyer M. Harmonic coordinates [M]. Pixar Animation Studios, Emeryville, CA, Pixar Technical Momo, 2006: 06-12.

[19] Lipman Y, Levin D, Cohen-Or D. Green coordinates [J]. ACM Transactions on Graphics (TOG), 2008, 27(3): 1-10.

[20] Wachspress E. A rational finite element basis [M]. New York: Academic Press, 1975: 49-51.

[21] Meyer M, Lee H, Barr A, et al. Generalized barycentric coordinates on irregular polygons [J]. Journal of Graphics Tools, 2002, 7(1): 13-22.

[22] Flanders H. Differentiation under the integral sign [J]. The American Mathematical Monthly, 1973, 80(6): 615-627.

[23] Silberberg E, Suen W. 经济学的结构——数量分析方法[M]. 3版. 张研, 译. 北京: 清华大学出版社, 2004: 125-140.

[24] Fabri A. CGAL-the computational geometry algorithm library [C]//Proceedings of 10th International Meshing Roundtable, Newport Beach, California, 2001: 137-142.

[25] Gleicher M. Generalized barycentric coordinates for mesh deformation [EB/OL]. (2011-05-11) [2014-03-10]. http://pages.cs.wisc.edu/～csverma/CS777/bary.html.

[26] Dunavant D A. High degree efficient symmetrical Gaussian quadrature rules for triangle [J]. International Journal for Numerical Methods in Engineering, 1985, 21(6): 1129-1148.

Approximation by Piecewise Function Based on Generalized Barycentric Coordinates and Voronoi Tessellation

Xiao Yanyang1,2, Tu Jincan1,2, Chen Zhonggui1,2

(1. Fujian Key Laboratory of Sensing and Computing for Smart City, Xiamen University, Xiamen Fujian 361005, China; 2. Department of Computer Science, Xiamen University, Xiamen Fujian 361005, China)

Under the generalized barycentric coordinates theory, we propose a new method to solve the problem of approximating a given function on the planar domain. To accomplishing this, an optimal piecewise function which based on the generalized barycentric coordinates is constructed. We use the Voronoi tessellation to create a partition of the domain, then an energy function that measures the approximation error is built. After deriving the gradient of the energy function, an efficient optimization method is adopted to update the tessellation. The optimal piecewise function will be constructed from the optimal tessellation. Due to its good ability of approximating discontinuous functions, our method can be applied to image approximation field. In order to demonstrate its efficacy, some experiments on analytic functions and color images are designed, which have produced good results.

generalized barycentric coordinates; function approximation; Voronoi tessellation; image approximation

TP 391

A

2095-302X(2015)03-0367-09

2014-10-08；定稿日期：2014-10-24

国家自然科学基金资助项目(61100107, 61472332)；中央高校基本科研业务费专项基金(厦门大学基础创新科研基金)资助项目(20720140520)

肖艳阳(1991-)，男，江西赣州人，硕士研究生。主要研究方向为计算机图形学。E-mail：jxndxyy@gmail.com

陈中贵(1982-)，男，浙江温州人，副教授，博士。主要研究方向为计算机图形学。E-mail：chenzhonggui@xmu.edu.cn