基于回归分析的航空器材消耗预测

刘臣宇 （海军航空工程学院，山东 青岛266041）

LIU Chen-yu (Naval Aeronautical Engineering Institute, Qingdao 266041, China)

0 引 言

影响航空器材消耗的因素多种多样，如：飞机的新旧、飞行任务类型、飞行时间、天气条件、机务人员维护飞机的水平等。飞机不同部位器材的消耗受到的影响因素也不同，如何正确确定器材的消耗规律，预测其消耗数量，关键在于找出影响器材消耗的主要因素和它们之间的关系。回归分析法是一种从因果关系出发进行预测的方法。它利用数理统计基本原理，在大量统计数据基础上，通过寻求数据变化规律来推测、判断和描述事物未来的发展趋势。

飞机起落架类器材在飞机起飞和降落时消耗比较严重，也就是说，起落架类器材的消耗数量与飞机的起落次数存在因果关系。如果能够建立飞机起落次数与器材消耗数量的回归模型，就能够根据未来飞机的起落次数预测器材的消耗数量。

1 模型建立

通过研究发现飞机起落架器材的消耗符合一元线性回归。一元线性回归模型的建立方法如下：假设变量X与Y有一定联系，二者通过观测或实验得到若干对数据：

如果这n个点的分布近似呈直线趋势，则方程：

称为这n个点的回归方程。这个方程的确定关键是找出系数a和b，其中b称为回归系数。

以下是求出a、b的过程：

在分布图上划一条直线，“使该直线最接近这n个点”，这条直线的斜率就是b，截距就是a，见图2。

图1 （X, Y ）的散点图

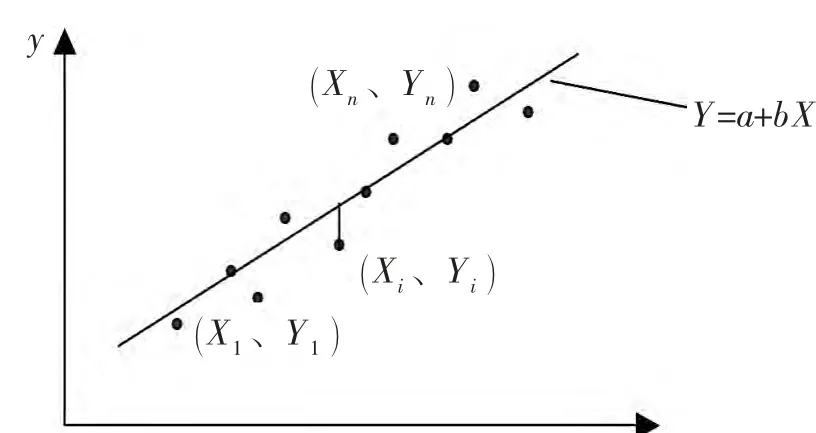
图2 X 与Y 的线性关系

为了使所画直线最接近这n个点，必须使线外的所有点到该直线的总偏差最小。

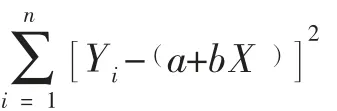
就是直线Y＝a+bX到这n个点的距离之和，该值是a、b的二元函数，记为Q（a、b）。即：

将Q（a、b）分别对a,b求一阶偏导数并令其为0，即可求出a、b。

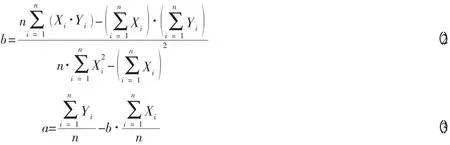
将a、b值代入（1） 式就建立了X,Y的线性回归模型[1]。

2 相关性检验

回归模型建立后，必须进行相关性检验，检验的方法是计算其相关系数。相关系数反映Y与X的相关程度。相关系数的计算公式为[2]：

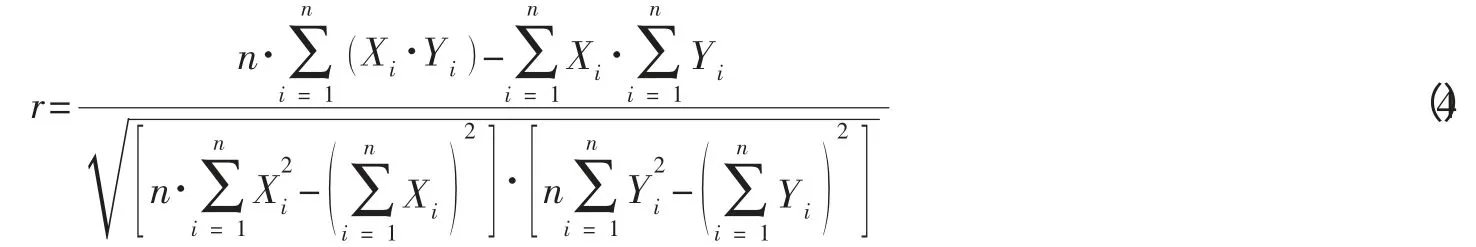
r一般介于0 和1 之间，即时，当接近1 时，表示Y与X的相关程度大，当接近0 时，表示Y与X的相关程度小。Y与X相关程度是否可以接受，可以通过与临界系数r0比较确定，r0可以通过样本数据的个数和显著性水平通过查表得到，当r大于r0时就认为Y与X相关。

3 置信区间

式中：Yi：第i个预测值；yi：第i个实际值。

由此得到修正的预测模型：Y=a+bX±2σ。

4 模型应用

某场站航材股通过对统计资料的分析发现，刹车片的供应量与飞行的起落次数之间存在因果关系，其统计资料如表1。试建立它们之间的回归模型[5]。

表1 刹车片供应数量与飞行起落次数的统计数据

图3 刹车片的消耗数与飞行起落次数的关系

为了能清楚地说明问题，以飞行的起落次数为横坐标，以刹车片的供应量为纵坐标，将表1 的六组数据画在坐标平面上，得到A、B、C、D、E、F 六个点（见图3），可见刹车片供应数量和飞行起落次数之间存在线性关系。

由此得到刹车片与飞行起落次数的回归模型为：

由式（4） 得到：r=99.7%，可以看出刹车片的消耗数量与飞行起落次数具有强烈的相关性。

应用式（6） 进行预测得到表2：

表2 刹车片供应数量的预测值

由表2 和式（5） 可以求出标准差：σ=2.5，置信区间为2σ。

因此，刹车片供应量和飞行起落次数之间的关系为：

结论：当确定了下年度的飞行起落次数时，就可以预测下年度刹车片的供应数量。

5 应用注意事项

（1） 回归分析法在应用时应选择样本较多的器材，即历史数据要多；

（2） 根据所选取变量的散点图，确定它们是否具有线性相关关系，只有近似呈线性关系的两个变量才能应用线性回归方法建立预测模型；

（3） 预测模型建立后必须进行相关分析，只有满足相关系数大于临界相关系数的模型才可靠，所求的误差（置信区间） 才较小，预测的结果准确。

[1] 唐纳德·沃特斯. 管理科学实务教程[M]. 北京：华夏出版社，2000.

[2] 浙江大学数学系. 概率与数理统计[M]. 北京：高等教育出版社，1979.

[3] 刘臣宇,等. 航材供应[M]. 北京：国防工业出版社，2009.

[4] 王攀，付光辉，戴琳. 偏最小二乘回归法在商品房销售价格分析中的应用[J]. 统计与决策，2014(7):84-86.

[5] 杨旸. 相依误差下线性回归模型最小二乘估计的相合性[J]. 统计与决策，2014(6):11-12.