泄量库容关系曲线法在某水库调洪演算中的应用

金美满

(温州市金秋建设工程咨询有限公司，浙江温州 325000)

1 引言

水库调洪演算计算方法有很多种，根据水量平衡原理而产生的计算方法有很多种，一般常用的有试算法、半图解法和简化三角形法等方法。

试算法可用于有闸门控制时的复杂泄流情况以及时段Δt内有变化时的情况，其缺点是计算繁琐、工作量大，较之笔算更适用于计算机程序计算。

半图解法也称单辅助曲线法、计算量较试算法小，但为提高辅助曲线的精度，Δt不能过大，并只适用于自由泄流及时段Δt固定的情况。

简化三角形法在复核小水库的防洪能力时较方便，但由于其前提是假定溢洪道无闸门控制，汛前水位与堰顶平齐，下泄流量过程呈直线变化，入库流量过程为曲线型或概化为三角型，易降低计算结果的精确度，也不适用于有闸门控制的溢洪道，同时在由入库流量过程线与下泄流量过程线间的面积查q～v关系曲线得q'm时，若q'm≠qm，则需另设qm重新计算，其工作量较大。这些方法由于或是计算繁琐、计算量大，或是有一定的适用范围，或是影响精度。鉴此，笔者在黄坡水库设计中应用泄量库容关系曲线法进行了尝试。

2 调洪演算的任务、目的及基本原理

水库调洪演算一般都是在水工建筑物的防洪标准或下游防护对象的防洪标准一定的情况下，针对拟定的泄洪建筑物类型和尺寸方案进行的。通过各种方案所求得的最高洪水位和最大下泄流量，进行防洪效益和投资的计算分析，选择最优方案，从而确定调洪库容、坝高和泄洪建筑物类型、尺寸。其直接目的则是推求一定防洪设计标准的洪水下，水库最高洪水位与最大下泄流量之间的关系，或调洪库容与最大下泄流量之间的关系。

水库调洪计算的基本原理是在时段Δt内，进入水库的水量与流出水库的水量之差，应等于该时段内水库蓄水量的变化值，即水量平衡原理。用水量平衡方程表示为:

式中:Q1、Q2:时段始未的入库流量(m3/s);

q1、q2:时段始未的下泄流量(m3/s);

V1、V2:时段始未的水库蓄水量(m3);

Δt:计算时段(s);

ΔV:时段内水库蓄水变量(m3)。

3 泄量库容关系曲线法在调洪演算中的具体应用

在某水库溢洪道第二方案的设计中，为简化计算，减少调洪演算工作量，考虑到其特殊的泄流方式，同时也为尝试一下新的计算方法，决定采用泄量库容关系曲线法做顺时序调洪演算。

该水库其泄流方式拟采用控制泄流与自由泄流相结合的方式来调洪，在已计算设计洪水位H1=79.375m和校核洪水位H2=80.933m之后，对控制段溢流堰型式、堰顶高程及宽度进行了选择，拟定堰顶高程73.00m，净宽30m，采用无底坎宽顶堰型。

根据前期的宽顶堰水力计算列出水位、库容和下泄流量关系表(见表1)。

表1 某水库水位、库容和下泄流量关系表

表1中:h=H－h堰

式中:h:堰顶水头(m);

H:水库水位(m);

h堰:堰顶高程(m)。

式中:Q:下泄流量(m3/s);

σs:淹没系数;

B:溢洪道净宽(m);

Ho:考虑行进流速水头的堰顶水头(m);

m:流量系数。

根据大(2)型水库防洪标准，其设计频率和校核频率分别按0.5%和0.05%计算，由表1中的库容和下泄流量绘Q～V曲线，用泄量库容关系曲线法作顺时序调洪演算(见图1，图2)

图1 某水库调洪计算Q～V曲线

经调洪演算得最大设计泄洪流量qm=767.50m3/s，最大校核泄洪流量qm=1052m3/s。

图2 某水库调洪计算(泄量库容关系曲线法)

由宽顶堰计算公式:Q=σsmB

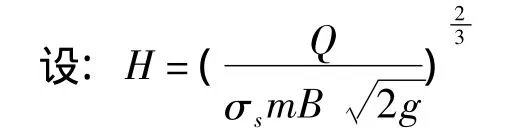
则:设计水位时堰顶水头h1=6.376(m)

故:H1＇=h堰+h1=73.00+6.376=79.376m≈设计水位H1

校核水位时堰顶水头h2=7.868m

H2＇=h堰+h2=73.00+7.868=80.868m≈校核水位H2

该方法经与试算法比较，其最大设计泄洪流量和最大校核泄洪流量分别仅有0.56%、0.78%的差异，该工程设计通过上级主管部门技术审查，满足实际工程需要。

4 结语

在对泄量库容关系曲线法的应用中，经与试算法、半图解法、简化三角形法相比，有如下特点。

首先，泄量库容关系曲线法既可用于有闸门控制时复杂泄流情况，也可用于无闸门控制的自由泄流情况。同时，对时段变化也无限制。

其次，该方法计算量小，不需试算，也不需作辅助线用图解演算，在整个计算过程中，只需作一条Q～V曲线，即可在已知洪水过程和时段未泄量时，求得初始泄量q。和相应的汛前库水位即进行逆时序调洪演算;也可在已知汛前库水位及相应的初始泄量q。和洪水入流过程Q～t时，求得最大泄量qm，即进行顺时序调洪演算，使该方法在计算速度及计算精度上均能满足要求并有广泛的适用性。

通过对该方法的实际运用及与其它计算方法的比较，笔者认为在大中型水库尤其是采用控制泄流或控制泄流与自由泄流相结合的方式来调洪并有时段变化的水库规划设计及编制水库控制运用方案中，采用泄量库容关系曲线法进行调洪演算是目前较为理想的一种计算方法。