我国城市房价波动的溢出效应研究
——基于DCC-MVGARCH模型的视角
张 谦 王章名 王成璋
(西南交通大学经济管理学院 四川成都 610031)
我国城市房价波动的溢出效应研究
——基于DCC-MVGARCH模型的视角
张 谦 王章名 王成璋
(西南交通大学经济管理学院 四川成都 610031)
运用动态因子分析方法对我国35个大中城市的房地产发展水平进行综合评价。在此基础上,选取发展水平较高的10个城市,利用其2007年7月~2014年9月新建商品住宅销售价格指数的月度数据,构建DCC-MVGARCH模型,研究这段时期内我国城市房价波动之间的溢出效应。结果发现,绝大多数城市房价波动间有着显著的正相关性,并且调控政策的出台在一定程度上降低了它们之间的动态相关系数。进一步的研究表明,我国城市房价波动之间存在一定的溢出效应,房价波动主要由房地产发展水平较高的地区传递至发展水平较低的地区。
房价;溢出效应;动态因子分析;DCC-MVGARCH模型
一、引言
房地产业价格水平的高低不但决定着房地产行业自身能否健康发展,同时对关联行业的发展、经济发展、居民生活质量、国家金融安全等方面产生影响,特别是对社会公平与稳定将产生巨大影响。
自1998年房地产业市场化改革以来,我国住房价格总体上一直处于上升的阶段,尤其是北京、上海、广州等东部地区的房价已经远远高于中西部地区。进入2014年,不少城市的房价增长减慢甚至出现了下降,再次激发了人们对房地产市场是否进入拐点的热议。这些城市房价变化是否会影响到其他地区的房价波动,不同地区的房价波动间是否存在内在联系,以及是否受到一定机制的影响,是值得我们探究的问题。
二、文献综述
Holmans AE(1990)通过对20世纪60年代至90年代的英国区域房价的分析计算,发现以伦敦为主的南部地区的房价首先变化,并逐渐由南至北影响整个英国房价的波动,并将其定义为房价的“波纹效应”(rippl effect)。它表示某些区域的住房价格波动由中心城市/核心地区带动而对其他城市/区域的住房价格的波动产生传导效应的长期关系。在其他学者关于房价的研究当中,相似的现象被称作扩散效应、空间效应或者连锁效应。本文将这种现象称为“住房价格波动的溢出效应”,即一个地区住房市场的价格波动会对另一个地区的房价波动产生影响。
近些年来,国内外学者在研究房地产价格波动溢出效应方面,采用不同的方法进行了一定的研究和探索。Hui(2010)运用协整检验和格兰杰因果检验方法,发现马来西亚三个城市房价变动之间存在相互影响;Holly和Pesarana(2010)运用空间计量方法对美国49个州29年的房价数据进行分析,在控制了实际收入等其他影响的条件下,发现空间因素依然对房价波动有重要影响;Bandt、Barhoumi和Bruneau(2010)将这类研究扩展到经合组织的成员国,研究表明美国实际房价直接或者间接地影响了其他国家的房价;Lee和Chien(2011)运用最新的单位根检验方法分析台湾地区1993-2009年各区域房价,结果显示除了台北以外其他地区的房价都具有显著的扩散效应,同时认为它是由公共住房较小和住房预售制度造成的;Simo-Kengne、Bitten⁃court和Gupta(2012)考察了南非9省房价对经济发展的影响,建立的空间SUR模型,显示空间效应是非常重要的影响房价因素;Lean和Smyth(2013)运用单因素和面板LM单位根检验方法考察了马来西亚14个区域5种不同房屋类型的价格指数之间的关系,发现在马来西亚的区域房价是从最发达地区传递到欠发达的地区;Ferrari和Rae(2013)的研究认为是人口迁徙,尤其是选择性迁徙,影响了英国住房价格空间上的分化;Liu和Roberts(2013)从逆城市化的角度运用向量误差模型考察香港各区域房价之间的相互依赖关系,结果显示香港地区的房价从中心城区向农村地区扩散效果大于逆城市化过程;Zhu等学者(2013)研究1995-2009年美国19个区域住房市场上收益率的非系统风险和波动率的空间联系,结果表明整个市场的联动不仅影响空间上相邻的地区,同时还影响到经济水平相近的地区,此外由于次贷危机的蔓延,使整个住房市场的空间影响更为强烈。
国内学者对住房价格波动溢出的研究还处于探索阶段,主要集中在验证我国的区域房价波动溢出效应是否存在,仅有少部分学者进一步研究房价空间扩散的路径。梁云芳和高铁梅(2007)以区域差异为视角,其研究显示房价波动在区域具有差异性,同时通过实证分析发现各区域间价格波动差异主要是由于货币政策效应以及房价的预期差异所造成的;洪涛等(2007)在面板数据模型的基础上,运用CSD检验进一步分析其残差得出,不同城市间房地产价格存在联动性;李永友(2014)通过IVQ R和空间计量分析指出,我国城市房价出现全域性的上涨,主要源于价格变化的自身惯性、需求驱动以及房价变化的“波纹效应”,同时通胀的影响会导致波纹效应的减弱;王锦阳和刘锡良(2014)运用脉冲响应函数对北京、上海、天津和重庆的房价数据泡沫分析发现,四城市房价泡沫间存在广泛的溢出效应,但影响方向和强度具有显著的差异;梁云芳和行成生(2012)利用动态因子模型对26个大中城市的房价波动进行因素分析,表明代表区域特征的区域因子对于区域内的城市房价波动影响较大,同时我国城市房价的波动存在由东部发达地区向中、西部地区蔓延的“波纹效应”。
从以上国内外研究来看,国外学者的研究比较丰富,他们通过多种方法证明了房价波动溢出效应广泛存在于各个国家和地区,同时部分学者进一步发现房价波动大多是由经济或房地产发展迅速的发达地区传递至欠发达地区。而国内的相关文献相对较少,现有的研究焦点主要侧重于利用统计检验和空间计量方法验证我国区域房价波动是否存在溢出效应,而对于房价波动溢出的具体传导路径的研究分析在国内几乎没有。基于上述原因,本文对已有研究做了进一步拓展,通过运用DCCMVGARCH模型研究我国不同城市房价波动间的动态相关性,同时探究我国城市间房价波动溢出的传导关系。
三、理论分析
关于溢出效应的相关研究,主要集中在区域经济学和金融学的相关领域。借鉴这些研究成果,结合住房商品的基本特征,本文将“住房价格波动的溢出效应”定义为:不同区域住房市场的价格波动之间可能存在某种传导或扩散机制,从而导致一个地区住房市场的价格波动会对另一个地区的房价波动产生影响,它反映的是在空间和时间两个维度上,两个或多个不同地区住房市场的价格波动之间的相互关系。同时学者们对于房价波动溢出效应的形成机理还未达成共识,具有代表性的主要有以下四种观点:
(一)人口迁徙
这种观点认为,居民会更倾向于迁徙到住房价格相对较低的地区,从而导致房价较低地区的住房需求量上升,最终引发价格的上升。然而这种观点在省域和城市层面缺乏有力的经验证据支持。根据2010年第六次人口普查数据显示,2005-2010年期间人口迁入比率较大的省域分别是上海(22.7%)、北京(21.6%)和浙江(16.3%)等经济发达地区,而这些普遍是房价较高的地区。这在一定程度上说明家庭在选择迁徙时不仅会考虑到房价的差异,同时可能更多受到就业机会等因素的影响。
(二)空间套利
这种观点认为,如果住房市场是有效的,那么套利行为将会消除地区间住房投资收益的差异;居民的住房投资需求比住房消费需求更容易产生空间套利行为,也就是说当拥有住房的居民有实力进行住房投资时,财富的转移引起了某种意义上的“人口迁徙”,从而将本地区的房价波动传递到另一个地区。
(三)影响房价因素的溢出效应
这种观点认为,即便是房价波动不存在空间联系,但是当决定房价的变动因素存在溢出效应,也会使得房价波动出现类似的表现。潘文卿(2012)认为我国区域经济增长存在空间溢出效应,同时经济基本面对房价有显著的影响,那么可能会导致观察到房价波动的溢出现象。此外,各类影响房地产市场的政策在不同区域的作用时间也会有差异,从而可能会表现出房价波动的溢出。
(四)信息传递
这种观点认为,地区间房价溢出效应的发生可能是由于房价波动之后,信息通过个体接触、新闻和网络媒介在空间逐渐传播,邻近地区间的价格关系可能会更强,因为信息可以传递得更快。这种传递不仅会作用于相邻的地区住房市场间,同时由于信息传递渠道的不断发展,在不相邻的城市间,信息的传递可能不再受地理区域的限制。一个或多个地区的住房市场作为信息源将信息传递到目标城市,但可能传递的发出时间或接受时间不同,速度不同或者完整性不同。国家统计局每月公布的《70个大中城市住宅销售价格指数》是反应我国各城市房地产发展的重要风向标,受到了社会的广泛关注。本地住房市场以及其他地区的房价变动情况,都会对消费者和房地产企业的预期产生重要的影响,而预期价格是影响房价变化的重要因素(况伟大(2010))。
四、房地产发展水平评价
本文主要研究的是我国大中型城市房价波动溢出效应。为了选取出更加具有代表性的样本,本文运用动态因子分析《中国房地产统计年鉴》中35个大中城市的房地产发展水平进行客观评价,通过分析结果,选取出适当的样本进行下一步研究。
(一)研究方法简介
动态因子分析的原理主要是将变量分解成两部分,截面部分利用主成分分析得到结果,另一部分通过线性回归得到分析结果,最后将两部分结果进行综合分析。假设数据X(I ,J,T)={Xijt},i=1…I,j=1…J,t=1…T,其中i代表主体,j代表变量,t代表时间。
首先通过计算可以得到其方差和协方差矩阵S,再将S分解成相互独立的方差或协方差矩阵:
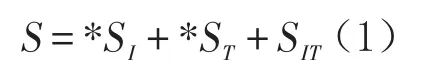
其中*SI代表各主体跨期的平均方差或协方差矩阵,它体现了各主体在不考虑时间维度变化影响的静态相对结构差异。*ST是各时期的平均方差或协方差矩阵,代表了不考虑个体因素影响的在时间维度上总体的动态差异。SIT是个体和时间交叉作用的方差或协方差矩阵,体现了主体总体平均水平变化和单体变化在时间维度上所导致的动态差异。
进而将式(1)变化为两部分

表1 动态因子分析中公因子的相关计算结果
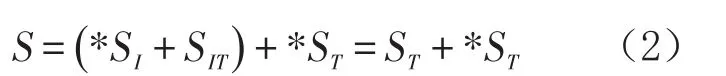
其中,ST可同过主成分分析得出各时期平均离差矩阵,*ST可以利用线性回归模型得出不同时期的变化。
(二)数据来源
这部分数据主要来源于2006-2013年的《中国房地产统计年鉴》和《中国统计年鉴》。主要选取的指标如下:代表房地产企业投入状况的本年完成投资(万元)和房地产企业从业人数(人),反应产出情况的房屋竣工面积(平方米),表示产业规模的房地产企业个数(个),反应市场状况的商品房销售额(万元)、商品房销售价格(元/平方米)和商品房销售面积(平方米)。
(三)计算结果与结果分析
运用stata软件,可以测算出各公因子的方差贡献率、累计方差贡献率和特征值。具体结果见表1。
由表1的计算结果可以看出第一、二个公因子的特征值分别为59.275和8.345,均大于1。同时它们的累计方差贡献率达到0.899,两者的值共同反映出各变量综合信息的程度大于85%。说明第一公因子和第二公因子可以体现指标中的主要信息。因此提取第一公因子和第二公因子作为城市房地产发展水平的计算因子,进而对35个大中城市的房地产行业发展水平进行计算和评价。
进一步通过第一、二公因子计算出各城市房地产行业发展水平的静态得分和动态得分,并根据平均综合得分对其进行排序,结果见表2。
根据结果可以发现城市房地产业发展位列前十的城市分别是北京、上海、重庆、成都、广州、天津、杭州、沈阳、深圳和武汉,它们的平均得分和静态得分都大于0,同时这些城市多位于在全国或者所在区域中经济较发达的地区。其他城市都处于平均水平之下,后十名分别是青岛、石家庄、南昌、太原、乌鲁木齐、银川、兰州、呼和浩特、海口和西宁,这些城市大多位于中西部欠发达地区,说明动态因子分析所得到的结果具有较高的可信度。
五、房价波动溢出效应分析
通过上一节动态因子分析的研究结果,本文选取了房地产发展水平相对较高的北京、上海、重庆、成都、广州、天津、杭州、沈阳、深圳以及武汉为研究对象,进一步运用DCC-MVGARCH模型考察不同城市间房价波动的动态相关性和房价波动的溢出路径。
(一)方法简介
Engle(2002)提出的DCC-MVGARCH,为研究房价波动溢出效应提出了新的思路。此外Hansen和Lunde(2005)比较了多种类型的GARCH模型的解释能力后认为,在大量研究中广泛运用的GARCH (1,1)形式更加简约,同时没有明确的证据表明更复杂的GARCH模型在样本内解释或者预测能力上优于GARCH(1,1)的形式。

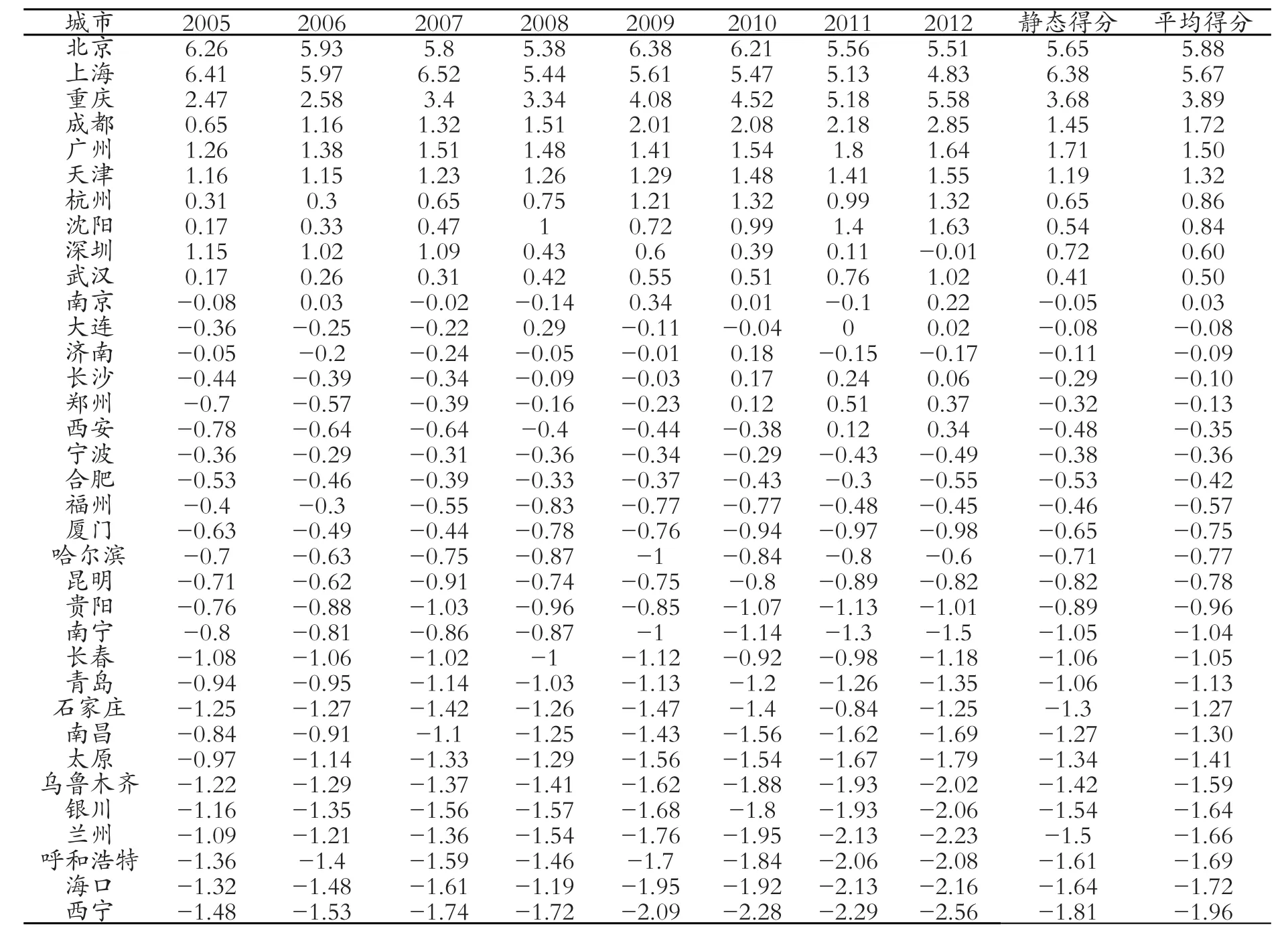
表2 35个大中城市房地产发展水平得分
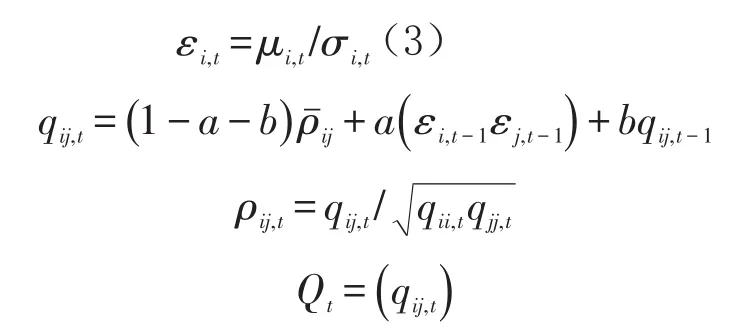

其中rt=(r1,t,r2,t,…,rn,t)T为t时刻n个城市房价波动率向量。i,j=1,2,…,n分别对应于不同的城市。mt为波动率向量r的条件期望。μ=(μ ,μ,…,μ)T
tt1,t2,tn,t是误差向量。Ωt-1为至t-1期所有能获得的信息集。σi2
,t为 μi,t的方差,其服从GARCH(1,1)模型。
diag(σ1,t,σ2,t,…,σn,t)是以σi,t为对角线上元素的对角矩阵。 ρˉij为εi,t和εj,t之间的无条件相关系数。qij,t为t时刻i与j地区房价波动率之间的条件协方差,且当i=j时qii,t表示t时期时i地区房价波动率的条件方差。Rt为所求的动态条件相关系数矩阵;a、b为待估计的参数,且当qij,t-1中i=j时qjj,t-1前面的参数b可以认为是度量所有地区房价波动率滞后一期对该地区i房价波动率的影响。模型通过两步骤进行估计,首先估计单地区房价波动率的GARCH过程,然后利用计算出的标准化残差,运用极大使然估计DCC模型中的参数a、b,最后计算出动态相关性矩阵Rt。
(二)数据选取
本文选取的研究对象是我国房地产发展水平较高的北京、天津、沈阳、上海、杭州、武汉、广州、深圳、重庆以及成都的房价波动率。样本范围从2005年7月至2014年9月,共111组房价变动月度数据。数据来源于中国统计局每月公布的70个大中城市房价数据中的新建商品住宅销售价格指数(上月=100),并通过简单的计算转换为各城市房价月度的变化率。此外通过ADF检验和PP检验结果(见表3)可以看出,十个城市的房价波动率都是平稳的,分析结果不会出现伪回归现象,可以进行下一步DCC-MVGARCH模型的分析。
(三)结果分析
根据Engle和Sheppard(2001)提出的两步估计方法,分析十个城市房价波动率的DCC-MVGARCH (1,1)模型。表4显示出了十个城市房价波动率之间的动态条件相关性的估计结果,可以发现我国发展水平较高的十个城市房间波动之间存在较强的正相关性。其中北京与其他绝大多数的城市在房价波动上具有显著的正相关性,上海、广州和深圳的房价波动率与大多数城市具有正相关关系,特别有趣的现象是成都与大部分城市的房价波动也存在显著的正相关性。
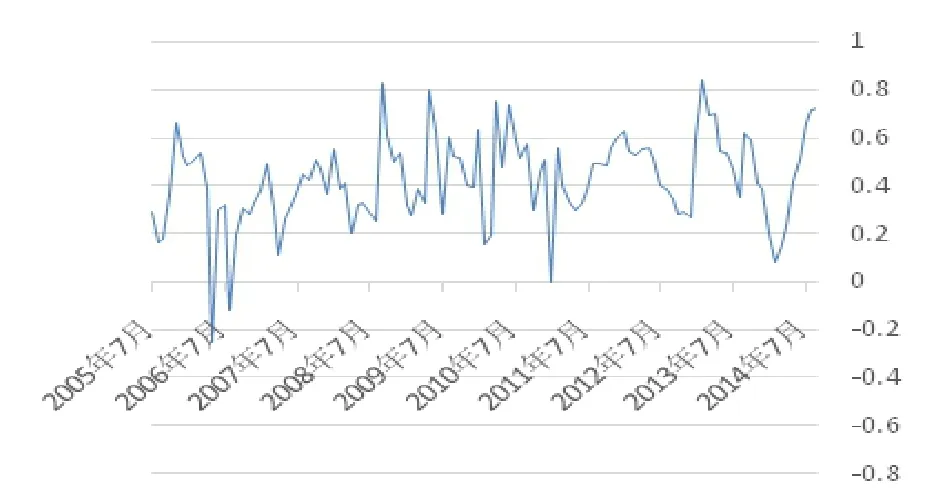
图1 北京与上海间动态条件相关系数

图2 广州和深圳间动态条件相关系数

表3 稳健性检验结果
为了更加准确地捕捉城市房价波动间相关系数的动态变化,本文描绘了北京与上海、广州与深圳两组动态相关系数图。从图1和图2中可以看出在次贷危机前中央政府出台一系列政策控制房价增长时,两组房价波动的动态相关系数波动大多围绕着零值波动,甚至出现较大的负值。但在次贷金融危机发生后,相关系数有比较明显的变化,自2007年之后两组城市房价波动剧烈的振动,但一直保持着显著的正相关性。同时可以发现一个有趣的现象,在2007-2013年间每当中央政府出台稳定房价增长的调控政策后,房价波动的相关系数在短时间内都会出现一个比较明显的下降,但一段时间后城市间的相关性又会逐步回升到较高的水平。例如2010年4月份中央出台的“国十条”和2011年1月公布的新“国八条”之后,两组相关系数都有着较大幅度的下降,而后又逐渐上升。这可能是由于地方政府和房地产市场对于中央政府调控政策的反应有差别,从而导致不同城市间的房价变化有差异。此外2014年以后全国的房地产市场都处于一个调整时期,大部分地区的房价有所回落,使得房价波动的相关系数又有了明显的增加。

表4 DCC-MVGARCH模型估计结果
前文已经考察了城市间房价波动的动态相关性变化,但是结果不能反映房价波动溢出效应的传导关系。因此为了进一步考察不同城市间房价波动的传导方向,根据对式(3)中参数b的估计和检验,图3绘出了十个城市房价波动的传导关系图,它反映的是房价波动的长期影响关系。

图3 各城市间房价波动溢出效应的传导关系图
从结果中可以看出,在5%的显著水平下,上海市的房价波动对于其他九个城市的房价波动都有显著的正向影响。北京房价波动对于天津、杭州和广州的房价波动产生了直接的传导影响。天津的房地产市场在价格波动上对于深圳和杭州有着单向的溢出效应。广州与沈阳、武汉之间存在着显著的房价双向波动溢出关系。沈阳的房价波动还影响着深圳和重庆。武汉对天津也有明显的房价波动溢出现象。深圳的房价变化影响着重庆的房价变化。有趣的是,除了上海之外,重庆的房价波动对其他城市都有显著的传导影响,这可能与近几年重庆房地产市场的快速发展有着密不可分的关系。从表1中可以看出2005~2012年重庆的房地产发展水平增长迅速,在2012年的房地产发展水平得分为5.58,已经超越北京和上海排名第一。可能正是因为重庆房地产市场的快速发展,从而使得重庆市在房地产价格波动上对其他城市产生重要的影响。总体而言,我国房价波动溢出效应更多的是由房地产发展水平较高的地区传导至发展水平较低的地区,同时后者对前者有一定反馈作用,这一结论与国外学者的研究结论一致。
六、结论与对策建议
本文在用动态因子分析方法对我国35个大中城市的房地产发展水平综合评价,并选取排名前10的城市为研究对象的基础上,以2005年7月到2014年9月其新建商品住宅月度销售价格指数为样本数据,运用DCC-MVGARCH模型,分析我国城市房价波动溢出效应。研究表明:我国绝大多数城市房价波动间有着显著的正相关性,房价波动动态相关系数图显示,在次贷危机以后,中央调控房地产市场的相关政策出台对城市间房价波动的相关性有着较强的负面影响,但经过一段时间调整后,它们之间的相关系数又会恢复到一个较高的水平。我国城市之间的房价波动存在较强的溢出效应,这种房价溢出效应大多数是由房地产发展较发达的上海、重庆、北京等地区传递至欠发达地区,同时欠发达地区的房价波动对发达地区也存在一定的程度上的反馈。
为了保持我国房地产行业的持续稳定和健康发展,中央在出台相关调控政策时,需要充分考虑到房价波动溢出效应的存在,不仅要适时制定出适宜的调控政策,更需要加强对地方政府执行调控政策的监督管理。首先,根据地方房地产市场发展的实际情况,强化对调控政策地方细则的指导和审核,既要因地制宜避免“一刀切”的情况发生,又要防止地方政府对调控政策的变相抵制。其次,通过改革地方政府绩效考评制度、引入惩罚机制等方法,强化房地产调控政策执行的约束监督制度。最后,尤其需要重视房地产市场发展水平较高地区的房价变动情况,通过更加合理的方式方法,避免或减弱由这些地区房价剧烈波动所带来的全国范围内的影响。
[1]Beatrice D.Simo-Kengne,ManoelBittencourt,Rangan⁃Gupta.House Prices and Economic Growth in South Africa: Evidence From Provincial-Level Data[J].Journal of Real Es⁃tate Literature,2012,20(1):97-117.
[2]Bing Zhu,Roland Füss and Nico B.Rottke.Spatial Link⁃ages in Returns and Volatilities among U.S.Regional Hous⁃ing Markets[J].Real Estate Economics,2013,41(1):29-64.
[3]Chien-Chiang Lee,Mei-Se Chien.Empirical Modelling of Regional House Prices and the Ripple Effect[J].Urban Studies, 2011,48(10):2029-2047.
[4]De Bandt O,Barhoumi K,Bruneau C.The international transmission of house price shocks[M].Housing Markets in Eu⁃rope.Springer Berlin Heidelberg,2010:129-158.
[5]Ed Ferrari,Alasdair Rae.The spatiality of housing market volatility and selective migration[J].Town Planning Review, 2013,84(1):107-125.
[6]Engle R.Dynamic conditional correlation:A simple class of multivariate generalized autoregressive conditional heteroske⁃dasticitymodels[J].Journal of Business&Economic Statistics, 2002,20(3):339-350.
[7]Hansen P R,Lunde A.A forecast comparison of volatility models:does anything beat a GARCH(1,1)[J].Journal of ap⁃plied econometrics,2005,20(7):873-889.
[8]Holmans A E.House prices:changes through time at na⁃tional and sub-national level[M].London:Department of the Environment,1990.
[9]Hon-Chung Hui.House price diffusions across three ur⁃ban areas in Malaysia[J].International Journal of Housing Mar⁃ kets and Analysis,2010,3(4):369-379.
[10]HooiHooi Lean and Russell Smyth.Regional House Pric⁃es and the Ripple Effect in Malaysia[J].Urban Studies,2013,50 (5):895-922.
[11]Nan Liu,Deborah Roberts.Counter-urbanisation,plan⁃ning and house prices:an analysis of the Aberdeen Housing Market Area,1984-2010[J].Town Planning Review,2013,84 (1):81-105.
[12]Sean Holly,M.Hashem Pesarana,Takashi Yamagata.As⁃patio-temporal model of house prices in the USA[J].Journal of Econometrics,2010,158(1):160-173.
[13]Sheppard K,Engle R F.Theoretical and Empirical prop⁃ertiesofDynamic ConditionalCorrelation Multivariate GARCH[J].Social Science Electronic Publishing,2001.
[14]洪涛,西宝,高波.房地产价格区域间联动与泡沫的空间扩散——基于2000-2005年中国35个大中城市面板数据的实证检验[J].统计研究,2007,24(8):64-67.
[15]况伟大.预期、投机与中国城市房价波动[J].经济研究, 2010,(9):67-78.
[16]李永友.房价上涨的需求驱动和涟漪效应[J].经济学(季刊),2014,13(2).
[17]梁云芳,高铁梅.中国房地产价格波动区域差异的实证分析[J].经济研究,2007,8(1):33-142.
[18]梁云芳,行成生.动态因子模型在房价波动因素分解中的应用——基于中国26个城市房价波动的分析[J].数学的实践与认识,2012,24(6):7-16.
[19]潘文卿.中国的区域关联与经济增长的空间溢出效应[J].经济研究,2012(1):54-65.
[20]王锦阳,刘锡良.住宅基本价值,泡沫成分与区域溢出效应[J].经济学(季刊),2014(4):2.
On Spillover Effect of Chinese Cities'House Price Fluctuation -based on DCC-MVGARCH model
Zhang Qian Wang Xun-zhang Wang Cheng-zhang
(School of Economics and Management,Southwest Jiaotong University,Chengdu,Sichuan 610031)
After having done the comprehensive evaluation of the real estate developing levels of 35 large and me⁃dium-sized cities in China by means of dynamic factor analysis,10 cities with the higher levels are selected to study the spillover effect of these cities'house price fluctuation by referring to the monthly data of new commodi⁃ty house price index from July 2007 to September 2014 and building a DCC-MVGARCH model.The results show that it has a significant positive correlation between the most of the cities'house price fluctuations,and reg⁃ulation policies could reduce the dynamic correlation coefficients of them to a certain extent.Further studies show that there is some spillover effect existed between house price fluctuations of the cities of China,and the fluctuations pass on mainly from the areas with high levels of development of the real estate to less developed ar⁃eas.
house prices;spillover effect;dynamic factor analysis;DCC-MVGARCH model
10.16249/j.cnki.1005-5738.2015.04.029
F293.35
A
1005-5738(2015)04-187-008
[责任编辑:蔡秀清]
2015-09-10
2012年度国家自然科学基金面上项目“我国城市住房的消费和投资需求的微观计量分析与测度的应用”阶段性成果,项目号:71171169
张谦,男,汉族,四川成都人,西南交通大学经济管理学院博士研究生,主要研究方向为房地产经济学。

