在水利水电工程中如何解决UTM投影变形问题的探讨

杨贵崇 曹家印

在水利水电工程中
如何解决UTM投影变形问题的探讨

杨贵崇 曹家印

水电工程跨国任务与日俱增，涉及的区域比较广泛，由于其采用的参考椭球、地图投影方式、分带原则等与我们国内区别较大，在国内水电工程测量中大多采用高斯投影，采用克拉索夫斯基椭球，高斯投影3°分带，而国外这些地区普遍采用UTM投影，一般为6°分带。由于投影方式的不同，导致变形也不一样，一般投影变形涉及2个方面：一是地面水平距离投影到椭球面的长度变形；二是椭球面距离投影到投影平面的长度变形，在工程上“控制点坐标反算的距离应与实地量测的距离相等”，即设计距离与实测距离相等为原则。水利水电规范中要求，长度投影变形值不应大于5 cm/km，那么如何应对国际工程项目中测量的变形问题，具有重要的现实意义。

UTM投影 长度变形 工程投影面 工程投影带 投影计算

1 理论基础

1.1 UTM投影

UTM投影通称为“通用横轴墨卡托投影”，投影方法为：椭圆柱割地球于南纬80°，北纬84°两条等高圈，投影后2条相割的经线上没有变形，而中央经线上长度比m= 0.999 6，2条割线距离中央经线为180 km，此2处m=1没有变形。而高斯投影中央经线处m=1，距离中央经线越远变形越大，如图1所示UTM投影示意图。

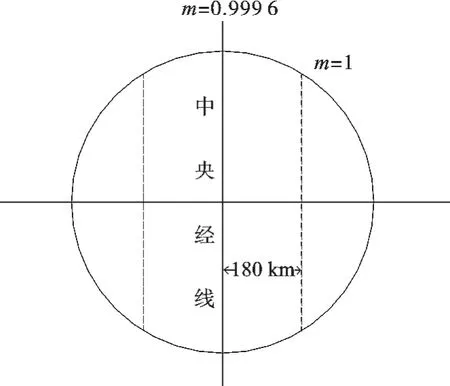
图1 UTM投影示意图

1.2 UTM投影变形

由高斯投影与UTM投影关系推导UTM的长度比。若高斯坐标分别用x高斯、y高斯表示，高斯投影长度比为m高斯，椭球半径为Rm，在高斯投影下长度m高斯=1+y2高斯/2R2m，而UTM投影的长度比mutm=0.999 6m高斯，yutm=0.999 6y高斯，由mutm=1+y2utm/2R2m推导出：

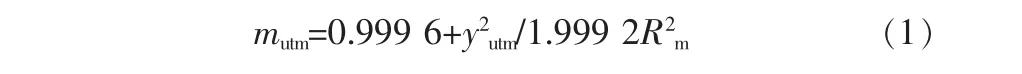
1.3 UTM投影长度变形量

投影变形实际上是投影长度比与1的差值，即参考椭球面至UTM投影面的长度变形值：

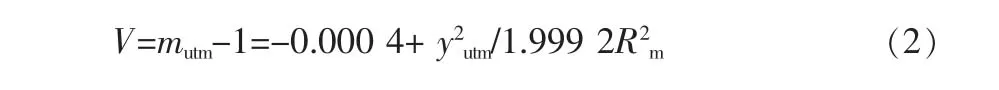
1.4 实量边长归算到参考椭球面上的变形影响

图2为地面边长投影至参考椭球面变形示意图。

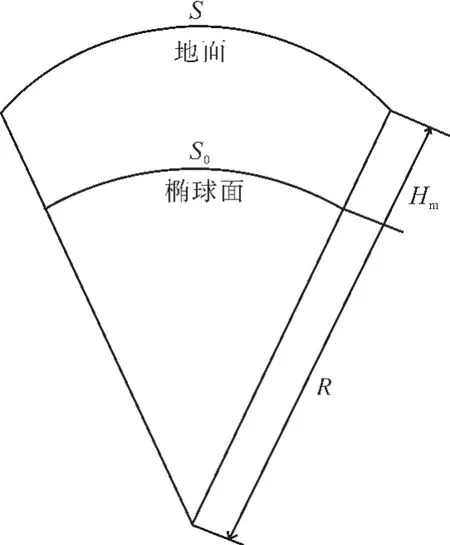
图2 地面边长投影至参考椭球面变形示意图

实量边长归算到参考椭球体面上的变形影响，由图2可知：

S/S0=（R+Hm）/R，推出S0=R×S/(R+Hm)，则变形量ΔS= S0-S=-Hm×S/(R+Hm)，由于R远远大于Hm，则R+Hm≈R，即

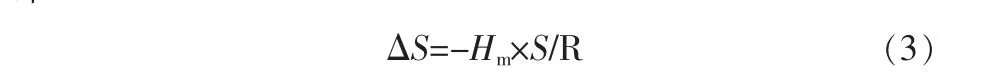
式中Hm——归算边高出参考椭球面的平均高程；

S——归算边的长度；

S0——参考椭球面上的长度；

R——归算边方向参考椭球法截弧的曲率半径。

由公式可以看出：ΔS的值总为负，即地面实量长度归算至参考椭球体面上，总是缩短的；ΔS值与Hm成正比，随Hm增大而增大。

1.5 地面边长投影至UTM投影面

此部分实际上由两部分影响，一是地面水平距离投影到椭球面的长度变形，二是椭球面距离投影到UTM投影平面的长度变形，即总的变形值Δ=ΔS+V=-Hm×S/Rutm-0.000 4+y2utm/1.999 2R2utm，当满足Δ≤5 cm/km时，为使测量结果一测多用，应采用国家统一的UTM投影坐标系，将观测结果归算至参考椭球面上。

当Δ＞5 cm/km时，则为保证测量结果的直接利用和计算的方便，可采用任意带的独立平面直角坐标系，归算测量结果的参考面可自己选定。

2 应用

2.1 工程概况

刚果（金）某水电站为低坝引水式水电站，主要由枢纽区、引水隧洞、厂房区等部分区域组成，整个测区南北长3 km，东西长5 km，测区平均高程为400 m，yutm=12 km，测区给定的坐标系统采用UTM投影，中央子午线为15°，R取6 356 816 m，经计算投影变形达到了-10.3 cm/km，超过了规范±5 cm/km的要求，无法满足施工精度要求。

2.2 工程投影面及投影带的选择

式（3）ΔS=-Hm×S/R为地面边长投影到椭球面边长变形量，若投影到某一高程面H0上，则其变形值为ΔS1=-（Hm-H0）×S/R，由于测区变形值超过了规范要求，为使Δ= -(Hm-H0)×S/Rutm-0.000 4+y2utm/1.999 2R2utm最小，设Δ=0，可以选择以下3种方式：第一种方式只改变H0；第二种方式只改变yutm；第三种方式既改变H0又改变yutm，在刚果（金）某水电站项目中采用了第三种方式，选取工程投影面为测区平均高程面400 m，则-(Hm-H0)×S/Rutm=0，要使-0.000 4+y2utm/1.999 2R2utm=0，经计算yutm=±179.8 km。测区中央子午线坐标（x=9 471 049.005 0，y=500 000）y坐标平移至179.8 km，则有（x=9 471 049.005 0，y=679 800）或（x=9 471 049.005 0，y=320 200）2种情况，按Clark1880椭球，计算出2处中央子午线经度分别为13°23'和16°37'。至此本项目采用了中央子午线经度为13°23'，投影至400 m高程面，作为工程坐标系。

2.3 GPS控制网的解算及其换带、投影计算

2.3.1 控制网点解算

整个工程区域共布设了18座GPS点，包括已知点3座，按三等精度施测，采用LGO1.6进行基线解算，天测GPSNET软件进行平差计算，整个控制网解算精度满足规范要求。

2.3.2 坐标换带、投影计算

由于GPS平差解算是在国家坐标下进行解算的，如变为工程坐标系下的坐标，需进行坐标换带及投影。由国家坐标系中央子午线为15°的坐标转换为13°23'的工程坐标，然后由换带后的坐标投影至400 m工程面。换带工作比较简单，在此不再赘述，坐标投影至投影面较为复杂。

坐标投影计算思路：坐标都可以表达为x=x0+D×cos α，y=y0+D×sin α，x0，y0为投影原点的坐标，D为投影原点到某点的距离，α为投影原点到某点的方位角。只要能求出D和α，则投影后的坐标即可计算出来。

2.4 投影关系的验证

为验证投影带及高程面的选择是否正确，利用全站仪进行GPS边长的检核，检核结果见表1。

表1 GPS控制点间反算距离与全站仪实测距离比较

从表1中可以看出，全站仪检测边长与GPS边长吻合较好，说明投影带及投影面的选择合理，边长变形问题得到了很好的解决。

P22

B

1007-6980（2015）03-0015-02

2015-05-29）

杨贵崇 男 工程师 中水北方勘测设计研究有限责任公司 天津 300222

曹家印 男 高级工程师 中水北方勘测设计研究有限责任公司 天津 300222