河流径流量分形方法在水库汛期分期中的应用
魏 炜李程程陈超基莫品疆
(1.广西交通职业技术学院,广西 南宁 530023;2.广西理工职业技术学校,广西 南宁 530031)
河流径流量分形方法在水库汛期分期中的应用
魏 炜1李程程2陈超基1莫品疆1
(1.广西交通职业技术学院,广西 南宁 530023;2.广西理工职业技术学校,广西 南宁 530031)
针对水库汛期分期常见方法主观性大,分期模糊的缺点,文章探讨基于分形方法以河流径流量为指标因子对广西澄碧河水库汛期进行分期。分期结果为:前汛期是4月13日至6月11日、主汛期是6月12日至8月30日、后汛期是8月31日至10月31日。分期结果与澄碧河水库1963~2011年49年间出现大洪水的时间分布相符。文章以水库上游的河流径流量为指标因子进行汛期分期,为缺乏实测入库洪水资料的水库进行汛期划分提供了参考。
汛期分期;分形方法;河流径流量;应用研究
1 引言
截止2012年,我国已建成各类水库9.7万座,水库供水总量占全国供水总量的32.3%[1],作为重要供水水源的水库,其运行调度在缓解水资源供需矛盾中具有举足轻重的作用[2]。目前,已有众多学者根据流域暴雨和洪水规律对流域汛期进行分期,针对汛期不同时期的洪水特性制定分期设计洪水,使水库以超汛限水位运行,实现洪水资源的安全利用[3,4]。在确保水库大坝及下游防洪安全的前提下,如何科学合理地制定汛期分期,实现洪水资源安全、有效利用已成为当下发挥水库兴利效益,缓解防洪兴利矛盾的研究热点。汛期分期的方法很多,其中常用的聚类分期方法有模糊集合分析法[5]、系统聚类法[6]、变点分析法[7]等,但都有着主观性大、分期模糊性大的缺点,因此,寻找一种简便且客观的汛期分期方法尤为重要。
曼德尔勃罗特(Benoit BMandelbrot)教授于1975年提出了分形的概念,其揭示了非线性系统中有序与无序的统一以及确定性与非确定性的统一[8]。根据分形理论的知识,受到确定性因素的影响而表现出一定时段的周期变化的水文过程,可认为其具有自相似性[9,10],故分形的定量化方法即分维。对于水库汛期中季节性和定时性径流量的变化可认为具有相似机制,因此,本文尝试以分形理论为基础,以入库河流径流量为指标因子对其汛期进行分期研究。
2 汛期分期中的分形方法
本文用容量维数对河流径流量的分形特征进行描述。分期的具体步骤如下[11]:
(1)取汛期内的样本点据系列X1,X2,…,Xn;
(2)根据样本时段的起始长度和步长跨度,确定某时段长T,单位为d;
(3)在时段T内选定能反映其样本的汛期分割水平Y的径流量,单位为m³/s;
(4)分别取时间尺度ε={1d,2d,…,10d},并统计样本Xi超过分割水平Y的时段数N(ε);
(5)根据该时段长T和不同时间尺度ε,按公式①计算与ε对应的相对时间尺度NT(ε);

(6)按公式②计算相对量度值NN(ε);
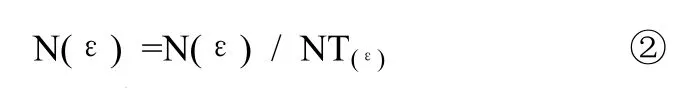
(7)计算与各时间尺度ε相对应的lnNN(ε)、lnε,并作lnε~lnNN(ε)相关图;
(8)在lnε~lnNN(ε)相关图上,选择无标度区间直线段并求出其斜率b,由公式③可求得容量维数Db;

(9)如果增大和减小时段长度T,重复(2)~(8)步骤所得容量维数Db基本相等,则T为同一个分期;
(10)重复上述(1)~(9)步,可确定汛期的分期。
3 实例分析
澄碧河水库位于广西壮族自治区百色市辖区,属于珠江水系,建库时间为1961年。水库总库容11.5亿m3,属大(1)型水库Ⅰ等工程,是一座以发电为主综合利用的大型水利工程。由于缺乏水库实测入库流量资料,所以无法对水库坝址洪水进行时序规律分析,但其上游有平塘水文站,距坝址39.6km,控制面积为1326km²,占坝址以上流域面积的67%,该站洪水资料较齐全,且历时较长,且水库流域同处一个气候区,洪水的成因是一致的,能代表该流域洪水的时序规律。故本文以平塘水文站实测的1963~2011年49年系列日均径流量为基础数据,用分形理论对其进行汛期分期。
3.1 汛期与非汛期的划定
笔者曾对澄碧河水库汛期与非汛期的划定进行了研究,在文献[12]中通过统计流域各旬暴雨次数的方法,将澄碧河水库的汛期划定在4月13日~10月31日,共202天。本文采用这一研究成果,作为澄碧河水库的汛期。
3.2 汛期分期研究
为了获得具备代表性的日均径流量数据,根据澄碧河水库 49年逐日长系列日均径流量数据,由式④可推求汛期 49年的平均日均径流量。

式中,
qij—系列中汛期某天的日均径流量,m³/s;
a —系列的起始年份,本文计算中为1963;
b —系列的结束年份,本文计算中为2011;
I —系列中的年份,本文计算中i={1963,1964,…,2011};
J —汛期中的某天,本文计算中j={4月13日,4月14日,…,10月31日}。
3.2.1 分维计算过程
考虑到汛期变化规律的季节性以及其成因的特点,分期不宜太短,一般以不短于30天为宜[13],因此本文起始计算时间段长T=30d。切割水平Y参照部份学者的计算经验,取该分期时段样本平均值的1.1倍时,此时所求的lnε~lnNN(ε)线性关系较好[11]。在计算过程中,本文先以 10d为步长进行维数计算,当容量维数值发生突变时,再缩短到5d为步长对该突变时间段进行加密计算,因此本文的计算精度为 5天。各分期计算过程如表1,各分期的lnε~lnNN(ε)相关线性图分别见图1、图2、图3。
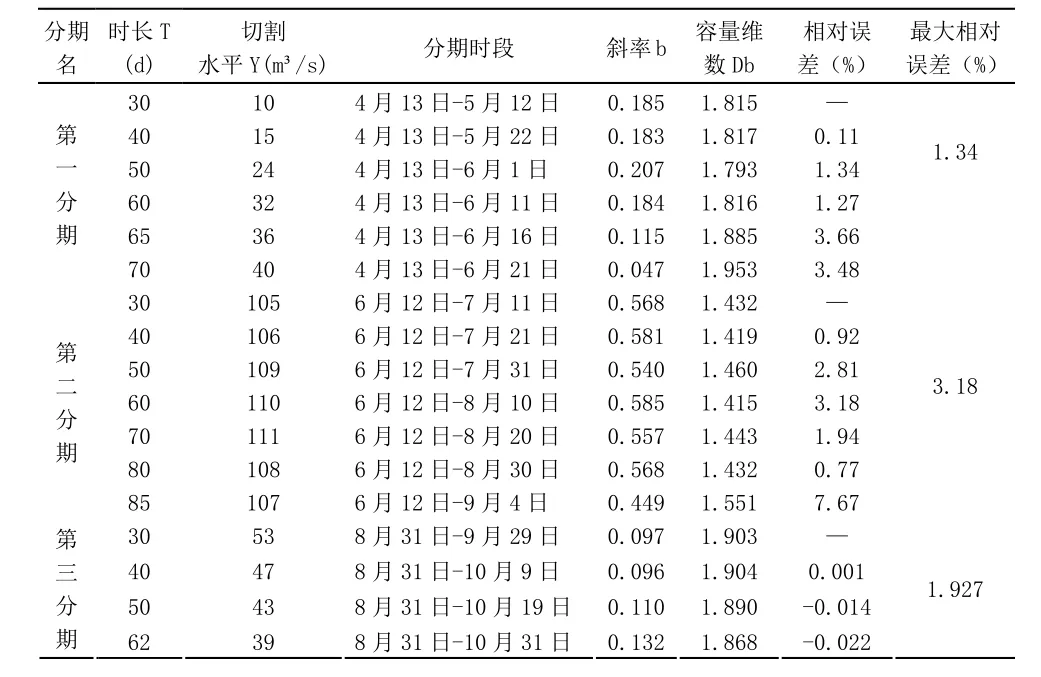
表1 澄碧河水库多年日均径流量分形方法分期过程表
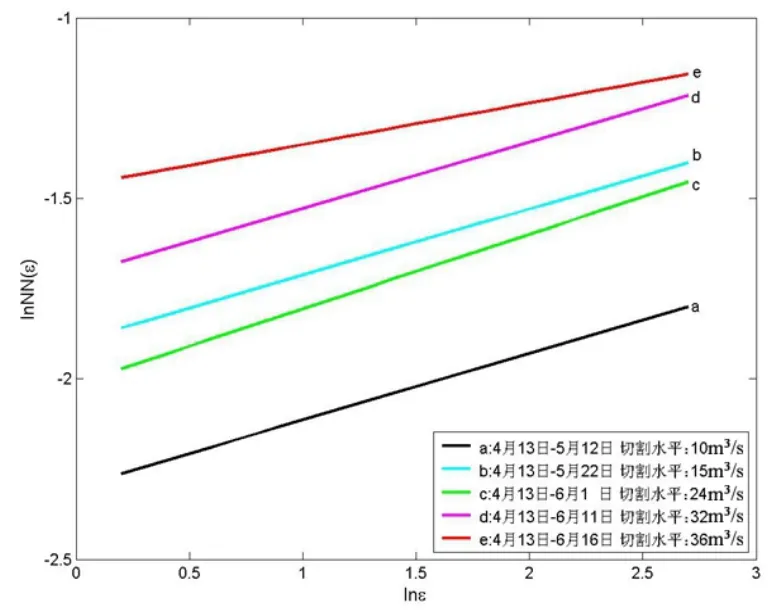
图1 第一分期lnε~lnNN(ε)线性相关图
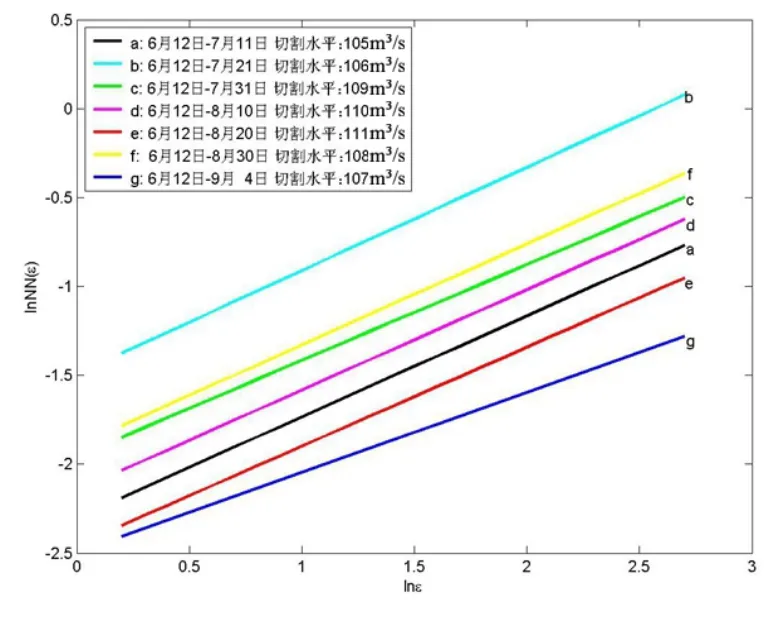
图2 第二分期lnε~lnNN(ε)线性相关图
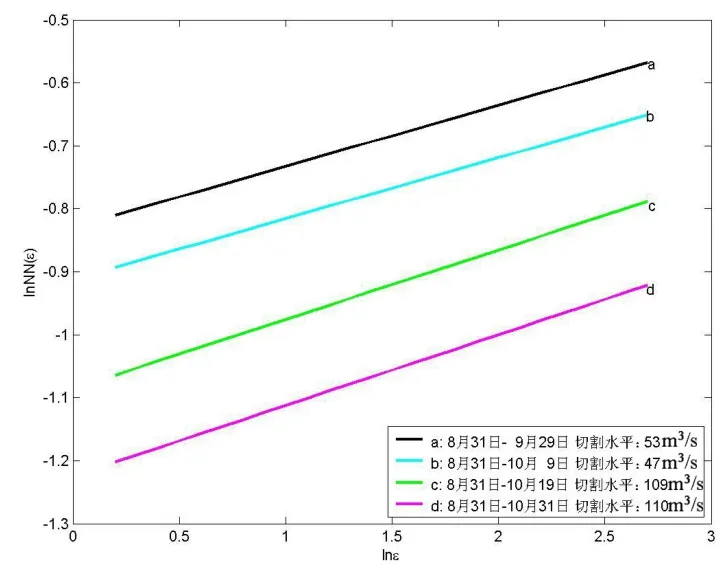
图3 第三分期lnε~lnNN(ε)线性相关图
从表1可以看出,在第一分期计算过程中,当T=30d、40d、50d和60d时,容量维数最大偏差值为0.024,最大偏差值与其中最小容量维数比值仅为1.34%,远小于5%,可以认为前面时段的容量维数基本相等,处于同一分期;当 T=70d时,容量维数值与前面各时段容量维数值相比发生了突变,最大偏差为0.16,最大偏差值与最小容量维数值比值为8.9%,超过5%,从图1也可看出,该时间段lnε~lnNN(ε)线性相关的斜率也有明显的突变,因此认为与前面时段不在同一分期。缩小步长,进一步计算,当T=65d时,容量维数值最大偏差为0.092,最大偏差值与最小容量维数值比值为5.13%,超过5%,图1也显示该时间段的lnε~lnNN(ε)线性相关的斜率与前面时间段斜率有较大变化,故认为与前面时段不在同一分期。由此,可确定汛期第一分期时间段为4月13日~6月11日。
同理从表1和图2可以看出,lnε~lnNN(ε)线性相关的斜率b在时段T=85时发生突变,前面各时段容量维数最大偏差值为0.045,最大偏差值与其中最小容量维数值比值为3.18%,斜率值也基本相等,可视为同一分期。相应地,汛期第二分期时间段为6月12日~8月30日。
同理从表1和图3可以看出,8月30日到汛期结束(10月 31日),各时段的容量维数值基本相等,最大偏差值为0.036,与最小容量维数值比值为1.92%,小于5%,lnε~lnNN(ε)线性相关的斜率也没有较大的变化,故可视为同一分期,故第三分期时间段为8月31日~10月31日。
因此,把汛期分为三期,以多年平均日均径流量为指标因子分期计算结果为:前汛期为4月13日~6月11日,主汛期为6月12日~8月30日,后汛期为8月31日~10月31日。
3.2.2 分期结果合理性分析
笔者根据1963~2011年澄碧河水库上游平塘站每年发生最大洪峰量及其出现的时间进行统计,其成果如表2。
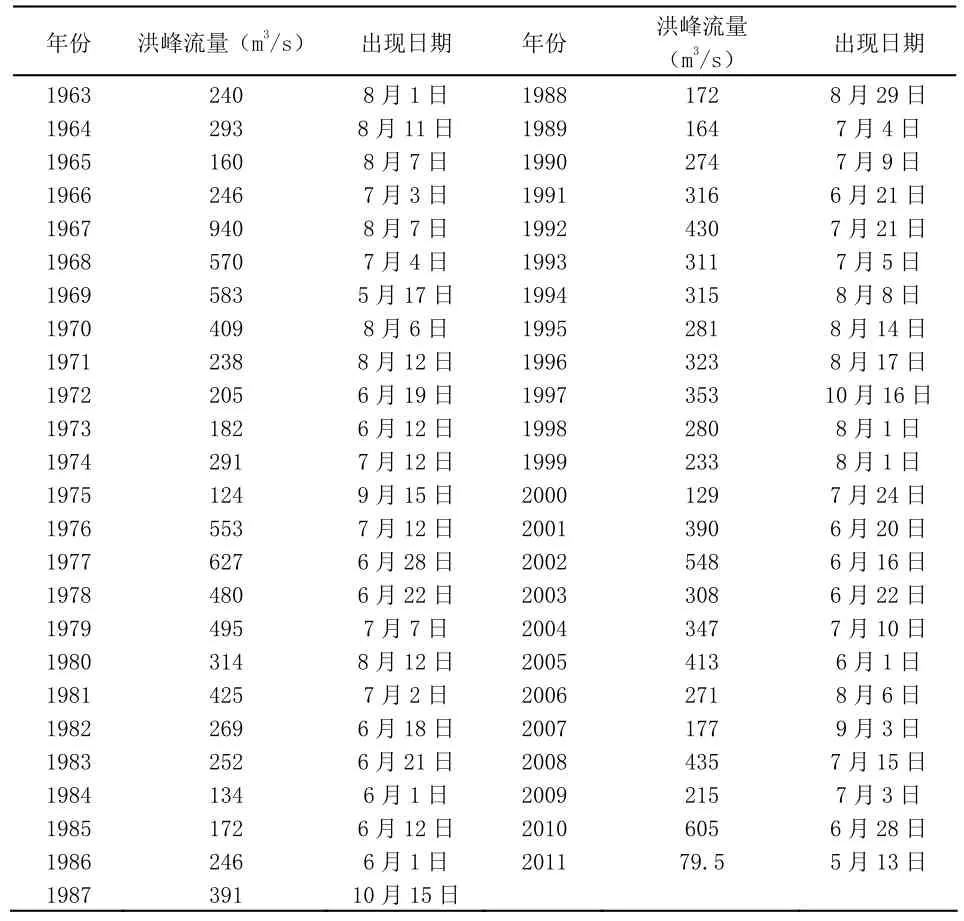
表2 1963~2011年澄碧河水库上游平塘站洪水信息统计表
根据本文分期结果,从表2可计算得到,在49年中澄碧河水库最大洪峰流量发生在主汛期内的为40个年份,占总年份的81.63%;发生在前汛期的为5个年份,占总年份的10.2%;发生在后汛期的为4个年份,占总年份的8.16%。由此可以看出,最大洪峰流量绝大部分出现本文划定的主汛期内。
对发生最大洪峰流量的量级进一步分析,49年中有14个年份的最大洪峰流量大于 400 m3/s,其中出现在主汛期内有12个年份,占85.71%。前汛期有2个年份的最大洪峰流量发生了大于400 m3/s,占14.29%。后汛期发生的年最大洪峰流量都小于400 m3/s,表明后汛期发生较大洪水的可能性较低。由此可知,大量级的洪水主要发生在本文划定的主汛期内。
综上分析说明本文对澄碧河水库汛期分期划定的结果是比较符合实际的。
4 结语
本文为分形理论在水库汛期分期中应用系列文章的一部分,主要研究了河流径流量为指标因子对澄碧河水库进行了汛期分期,依据澄碧河水库49年实测的每年最大洪峰流量出现的时间的分布,验证了成果的合理性。本文以水库上游的河流径流量为指标因子进行汛期分期,为缺乏实测入库洪水资料的水库进行汛期划分提供了参考。同时,分形方法的应用,减少了水库划分的主观性,提高了精确性。但是由于水文现象十分复杂,影响因素众多,因此相关的分期方法和理论需要进一步深入研究,以检验水库汛期分期的科学性。
[1] 中华人民共和国水利部.2011年中国水资源公报[M].北京:中国水利水电出版社,2012:3-15.
[2] 王国安.关于我国水库的防洪标准问题[J].水利学报,2002, (12):22-25.
[3] 贾函,周建中,杨俊杰,等.凤滩水库分期分级洪水的防洪调度研究[J].水力发电,2006,(1):19-22.
[4] 张秀菊,董增川,李秀平.基于洪水资源利用的汛期分期研究[J].水力发电,2008,(12):36-39.
[5] 陈守煜.从研究汛期描述论水文系统模糊集分析的方法论[J].水科学进展,1995,(2):133-138.
[6] 高波,刘克琳,王银堂,等.系统聚类法在水库汛期分期中的应用[J].水利水电技术,2005,(6):1-5.
[7] 刘攀,郭生练,王才君,等.三峡水库汛期分期的变点分析方法研究[J].水文,2005,(1):18-23.
[8] 张济忠.分形[M].北京:清华大学出版社,1995.
[9] 李长兴.论流域水文尺度化和相似性[J].水利学报,1995, (1):40-46.
[10] 丁晶,王文圣,金菊良.论水文学中的尺度分析[J].四川大学学报(工程科学版),2003,35(3):9-13.
[11] 方崇惠,雒文生.分形理论在洪水分期研究中的应用[J].水利水电科技进展,2005,25(6):9-13.
[12] 魏炜,莫崇勋,刘俐,等.流域降雨量分形方法在水库汛期分期中的应用[J].人民黄河,2014,36(10):39-41.
[13] 长江水利委员会.水利水电工程设计洪水计算规范SL44-93[M].北京:水利电力出版社,1993.
The application of fractal method of river runoff in flood season staging
In view of the disadvantages of the subjectivity and treservoir flood season staging in the common method,this paper explores the method of fractal theory for Chengbi river reservoir flood season installments,which is based on river runoff as the index factor.The results indicate that the pre-flood season is from April 13th to June 11th, the main flood season is from August 30th to June 12th, the after-flood season is from August 31st to October 31st. The results of the stage are consistent with the time distribution of the great flood in 49 years of 1963~2011.In this paper, the river runoff in the upper reaches is used as the index factor for flood season staging,which provides.reference for the flood data of reservoir flood data.
Flood season division;fractal theory;river runoff;applied research
TV697.1+1.
A....
1008-1151(2015)08-0020-03
2015-07-10
广西高校科学技术研究项目(KY2015YB417)。
魏炜(1988-),男,广西灌阳人,广西交通职业技术学院专任教师,硕士,研究方向为水文水资源及水工建筑物;陈超基(1990-),男,广西玉林人,广西交通职业技术学院教师,助教;莫品疆(1969-),男,广西上林人,广西交通职业技术学院教师,副教授。
李程程(1989-),女,湖南绍东人,广西理工职业技术学校专任教师,助理工程师。

