2013年四川芦山MS7.0地震自动速报震级偏差分析及方法改进

梁建宏 孙 丽 徐志国 刘 杰

1）中国北京100045中国地震台网中心

2）中国北京100081国家海洋环境预报中心

3）中国合肥230026中国科学技术大学地球和空间科学学院

引言

由计算机软件自动测定地震参数并完成发布已经成为全球地震台网的普遍做法.根据目的不同，发布地震参数的时间有长有短.例如地震早期预警在震后数秒至数十秒发布地震参数，海啸预警震后数分钟发布地震参数.相对于我国传统人工测定地震参数并在震后数十分钟完成发布的人工速报，本文所说的自动速报是指由计算机软件自动测定地震参数，通常在震后1—3分钟发布地震信息的过程.

大地震震级的自动测定无论是对地震早期预警、海啸预警等紧急地震警报的发布，还是对地震灾害的评估和判定都具有重要的应用价值.一系列快速测定震级的方法被提出，例如，用于地震早期预警的由初至P波数秒波形资料确定震级的方法（Wu，Teng，2002；Allen，Kanamori，2003；Wu et al，2006，2007；Yamada，Ide，2008；Yamada，Mori，2009；Allen，Ziv，2011），用于海啸预警的由P波或S波数十秒波形资料确定震级的方法（Tsuboi et al，1995，1999；Kanjo et al，2006；Zollo et al，2006；Hara，2007；Lomax et al，2007；Lomax，Michelini，2009；Katsumata et al，2013），以及用于一般为快速发布地震参数而使用的方法（Saul，Bormann，2007；Delouis et al，2009；Earthworm，2011；Vallée et al，2011；SeisComp3，2013）.然而，与经过人工仔细分析测定的震级大小相比，由计算机软件自动测定的震级或多或少存在偏差，特别是对于大地震震级，其偏差有时较大.分析导致这些偏差的原因，进而改进自动测定震级的方法，向政府和社会公众发布比较准确的地震参数具有重要的现实意义.

中国地震局于2013年4月开始正式向社会提供地震自动速报信息服务.自动速报信息通过多种手段实时向政府、媒体和社会公众发布，在政府应急响应和救灾决策以及引导社会公众知灾避灾中发挥了重要作用，产生了良好的社会效益.两年多的运行表明，地震自动速报信息服务能够在2分钟内发布国内地震参数，对于中小地震发布的参数比较准确，而对于强震发布的震级则往往偏小.

2013年4月20日四川芦山MS7.0地震是中国地震局正式向社会提供地震自动速报信息服务后遇到的第一个有社会影响的地震，震后57s发布了此次地震的震中和震级，发布的标准震级为M5.9；震后12分钟中国地震台网中心正式测定了此次地震参数，标准震级为M7.0.芦山地震自动速报发布的震级偏小较多，引起了一些社会公众和专业人士对地震自动速报服务能力的质疑.如何改进自动速报震级测定方法，提升自动测定地震参数的精准度是我们必须面对的问题.

1 芦山地震参数速报

目前对地震参数的发布采用先自动、后人工的两个阶段模式.首先由计算机软件系统发布自动测定的地震参数，然后人工发布正式测定结果.根据中国地震局颁布的《地震速报技术管理规定》，地震速报发布的震级为标准震级M，标准震级M由地震面波测定（国家质量技术监督局，1999）.实践中，若有面波震级，标准震级M 的大小就等于面波震级大小；若无面波震级，则将其它类型的震级用经验统计关系转换为标准震级.本文涉及的震级如未标明具体类型，均为标准震级M.

目前中国地震局共开发3套自动测定地震参数的软件系统，组成提供自动地震速报信息服务的支撑软件系统，部署在我国5个片区和2个地震台网中心，分别为东北、华北、西北、东南、西南5个片区的“区域自动速报软件系统”以及广东地震台网中心的“国家地震速报备份软件系统”和国家测震台网中心的“中国及全球地震自动速报软件系统”.

对于一次地震的自动测定，目前规定如果有两套以上的软件系统测定地震参数，国家测震台网中心的综合触发系统就会对外发布一个合成的结果.目前运行的3套自动测定地震参数的软件系统在测定区域地震震级时，普遍采用近震震级ML，并根据郭履灿①郭履灿.1971.华北地区的地方性震级ML和面波震级MS经验关系（全国地震工作会议资料）.于1971年由邢台地震余震资料得出的经验关系M＝1.13 ML－1.08，将ML转换为标准震级M.

2013年4月20日8时2分46秒，四川芦山发生MS7.0强烈地震.部署在不同片区和地震台网中心的3套软件系统以及国家测震台网中心的值班人员分别在不同时间速报了此次地震的参数，于震后57s对外发布了自动速报结果；震后12分钟，发布了人工正式速报结果.按照地震参数产出时序，给出了具体速报过程，如表1所示.

表1 芦山地震速报过程Table 1 The rapid information report history for the Lushan earthquake

由上述速报过程可见，与人工正式测定结果相比，各自动测定地震参数的软件系统产出的参数中震中经纬度误差较小，震级在不同的时间偏差不同，且用时越少，震级偏差越大.1分钟内产出的震级M＜6.0，2分钟左右产出的震级为M6.8，4分钟内产出的震级达到M6.9.可见，2分钟以后产出的震级接近人工正式速报震级.

作为自动速报信息服务三大支撑软件系统之一，中国及全球地震自动速报软件系统（以下简称自动速报系统）于震后56s发布了芦山地震震级为M5.8，这直接导致综合触发系统对外发布的震级为M5.9.本文以自动速报系统发布用时和中国地震台网连续波形记录为基础，大致还原了芦山地震自动速报系统的震级测定过程，分析了震级偏差较大的原因，并在此基础上提出了改进措施.

2 自动速报系统测定震级的偏差分析及方法改进

2.1 现行自动测定震级的方法

芦山地震发生前，自动速报系统在测定区域地震的震级时，采用近震震级ML.对于近震震级ML的计算，1959年李善邦将里克特采用的伍德－安德森测量ML的公式过渡到适用于中国台网短周期地震仪测算的ML震级中（国家地震局震害防御司，1992），其表达式为

式中，A＝（AE＋AN）／2为东西、南北两水平向位移记录最大值的平均值，R（Δ）李为量规函数.

按照ML震级定义及《地震及前兆数字观测技术规范》的要求（中国地震局，2001），若使用目前中国地震台网普遍部署的宽频带地震仪产出的记录计算ML，则需将宽频带记录仿真为短周期位移记录.传统的仿真方法主要为频域法，须在事件记录结束后才可以进行，不适用于近实时快速确定震级.金星等（2004）提出了在时域中将宽频带速度或加速度记录实时仿真为位移记录的方法.该方法可简化实时计算近震震级ML的步骤，提高了计算速度和效率.金星等（2004）提出的由地面速度时程计算位移时程的公式为

其中，

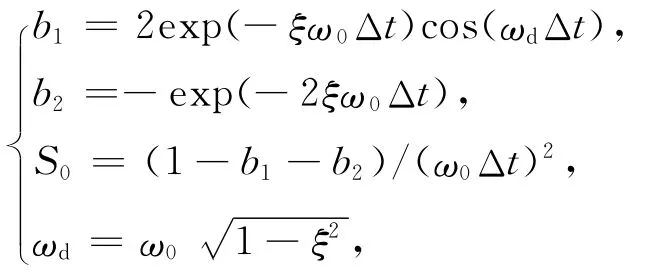
式中：xk为k点的位移；vk为k点的速度；Δt为采样间隔；δ为与Δt／T0有关的参数，取值为0.091 3；ω0＝2π／T0，T0为单自由度系统的自振周期；ξ为阻尼比.

将宽频带速度或加速度记录实时仿真为位移记录的方法具有速度快、精度高的特点，可广泛用于地震动参数的实时计算中.为了简单并易于实时计算，自动速报系统在测定震级时，将垂直向宽频带速度记录逐点实时仿真为短周期位移记录.随着时间的推移，不断获取和更新垂直向仿真短周期位移记录的最大值和最小值，将最大值与最小值的绝对值的和作为最大峰－峰值，代替式（1）中的A，并由式（1）计算近震震级ML.虽然这里A的取值与式（1）中A的规定取值有所不同，但实践证明该计算得出的ML与严格按照式（1）中A的定义计算出的ML差别很小.

同样在自动测定震级过程中，为了使数据处理得简单并把时效发挥到最大，对于每一个台站，即使S波（或Lg波）的最大振幅还未到达，也使用该台站的P波计算震级.对多个台站的ML取其平均值，这样，ML震级实时更新，直到事件结束，得到最终的ML震级.

2.2 芦山地震自动速报系统测定震级偏差的原因分析

中国地震局对外发布芦山地震自动速报结果是震后57s，考虑到数据包长度、信息流转和完成发布所需时间，产出此结果时可利用的波形数据大约到震后50s.根据地震走时表可知，从震中出发的P波传播50s时可到达的最远震中距约为3.1°（345km）.根据拾取到时需初至P波到达台站后持续一小段时间，以及从实时数据包到计算出震级中间处理过程所需时间计算，可用台站的最远震中距大约为320km.

芦山地震震中距380km范围内的台站分布如图1所示.各台站装配的均为宽频带地震仪.可以看出：在震中距320km范围内的可用台站共有40个，分布在图1中蓝色圆圈内，其中限幅台站23个，未限幅台站17个；靠近震中的绝大多数台站记录限幅.图2为震中距320km范围内部分台站的速度记录.

在震中距320km范围内，最近的MDS台记录限幅，其原始宽频带记录、仿真短周期位移记录、仿真短周期位移最大峰－峰值及ML随时间的变化如图3所示.可以看出在震后28s（实际为震后可用数据时间长度达到28s，后叙震后具体时间如无特别说明，含义与此相同），ML达到最大，其值仅为5.4.作为对比，较远的RTA台记录未限幅，其原始宽频带记录、仿真短周期位移记录、仿真短周期位移最大峰－峰值及ML随时间的变化如图4所示.可以看出在震后97s，S波最大振幅到达，ML为6.7.显然记录限幅的MDS台严重低估了震级的大小.

自动速报系统测定地震参数所使用的是靠近震中台站的波形数据，在测定芦山地震时对震级的量算方法和发布策略尚不完善，未考虑限幅记录的影响，因此将记录限幅的台站也参与到本次地震震级的计算中.图5给出了震中距320km范围内所有40个台站参与芦山地震震级测定时，平均ML随时间的变化.可以看出，震后0—60s为震级快速上升段，60—100s为震级平稳上升段.在震后50s时，平均ML为6.1，转换到标准震级为M5.8，该值与中国地震局对外发布的标准震级M5.9比较一致.由于在震后50s时，震级还处于快速上升段，因此此时计算的ML无疑会偏小.

通过上述对芦山地震自动测定震级过程的还原可知，此次地震自动速报震级偏小的原因有两个：一是自动速报系统在计算震级时使用了占较大比例的限幅记录，由限幅记录计算的过小震级（如MDS台的震级为M5.4）的贡献导致平均震级偏小；二是在发布此次地震自动速报参数的时间点上（此时可用波形截至震后50s），部分较远台站（如图4中的RTA台）的S波（或Lg波）未到达或未完全到达，其震级主要通过P波得到，故所得震级明显偏小，造成平均震级也偏小.

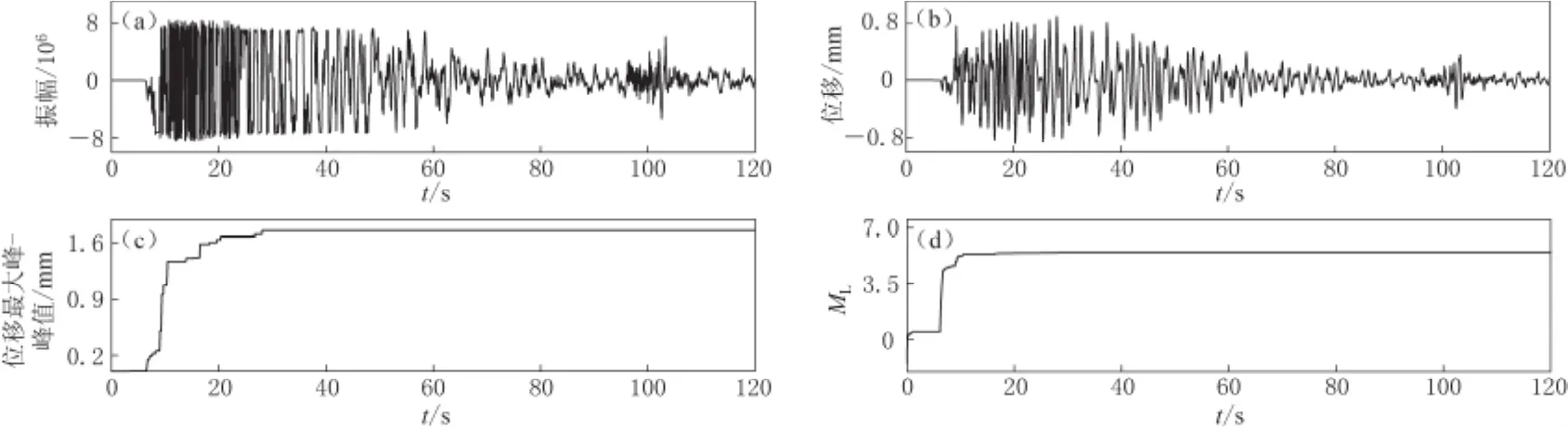
图3 MDS台由原始宽频带记录到得出ML的处理过程（a）原始宽频带记录；（b）仿真短周期位移记录；（c）仿真短周期位移最大峰－峰值；（d）ML随时间的变化Fig.3 The process from raw broadband seismogram to MLdetermination for the station MDS（a）The raw broadband seismogram；（b）The seismogram of simulated short period displacement；（c）The maximum peak-to-peak value of simulated short period displacement；（d）MLvariation with time

图4 RTA台由原始宽频带记录到得出ML的处理过程（a）原始宽频带记录；（b）仿真短周期位移记录；（c）仿真短周期位移最大峰－峰值；（d）ML随时间的变化Fig.4 The process from raw broadband seismogram to MLdetermination for the station RTA（a）The raw broadband seismogram；（b）The seismogram of simulated short period displacement；（c）The maximum peak-to-peak value of simulated short period displacement；（d）MLvariation with time

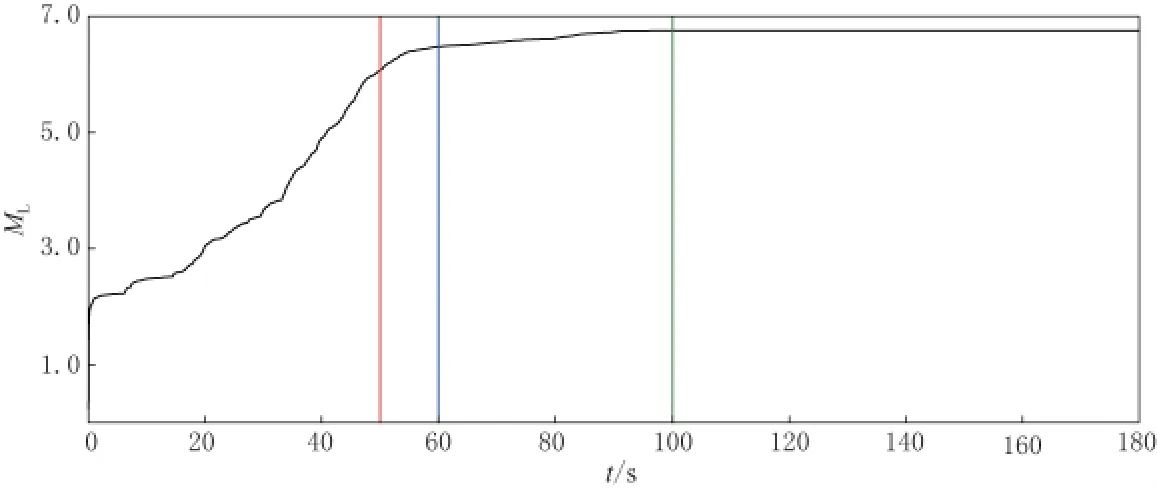
图5 由震中距320km范围内全部40个台站测得的平均ML随时间的变化红色、蓝色和绿色竖线分别表示震后50s，60s和100s的时间点Fig.5 Variation of mean MLdetermined by all 40stations within the epicentral distance of 320km with time The red，blue and green lines represent the time 50s，60sand 100sfrom origin time，respectively

需要指出的是，虽然自动速报系统在芦山地震定位和量算震级时实际使用的台站与本文使用的40个台站有些出入，但使用该40个台站计算震级的过程大致还原了自动速报系统当时测定震级的实际情形，因此由本文分析得到的自动速报震级偏小的原因符合实际情况.

2.3 对自动测定震级方法的改进措施

由于无法预知限幅的影响有多大，因此使用近台限幅记录参与震级计算显然不确定性较大.如果在某一震中距范围外，所有记录都不限幅，则如此计算的ML能够较真实地反映地震震级的大小.然而等待某一震中距范围外所有记录都不限幅需要付出时间成本，而自动速报的优势恰恰体现在时效上，因此需要在准确性和时效性之间折中.为此，我们设定两个震中距Δ1和Δ2，Δ1＜Δ2，Δ2－Δ1＝100km.在Δ1和Δ2范围内，如果可用地震台站数量大于等于20，且未限幅台站数与台站总数的比值大于0.75（即3／4以上的台站未限幅），我们就使用该震中距范围内未限幅记录计算ML，各台ML取其平均值，代表此次地震真实的ML震级.

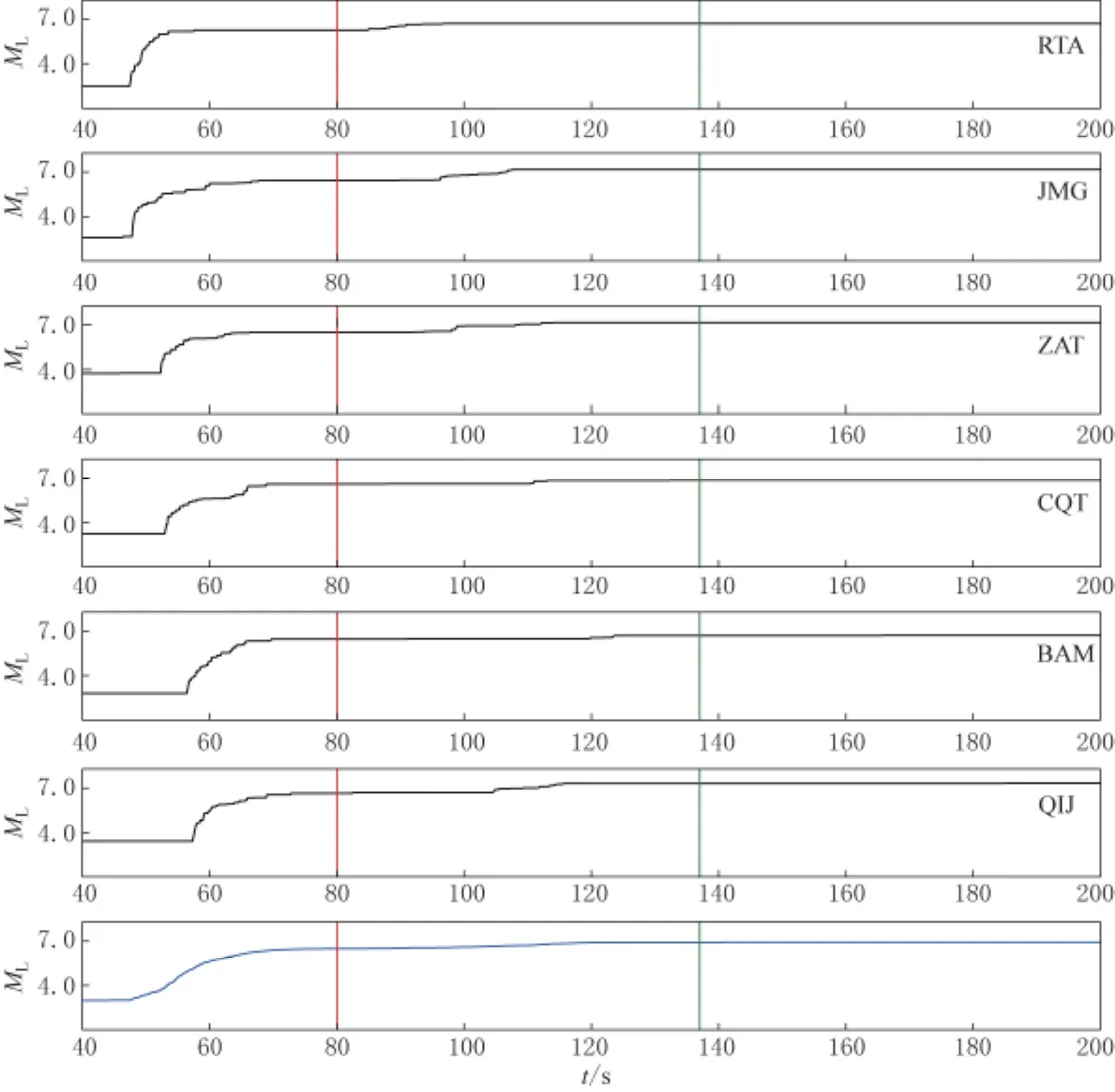
图6 由震中距280—380km范围内部分未限幅台站测得的ML及全部未限幅台站测得的平均ML随时间的变化黑色曲线和蓝色曲线分别为各台ML和平均ML随时间的变化，红色竖线和绿色竖线分别表示震后80s和137s的时间点Fig.6 Variation of MLdetermined by some stations without clipped records and mean MLdetermined by all stations without clipped records with time with the epicentral distances from 280km to 380km The black and blue curves represent the MLand the mean ML，the red and green lines represent the time 80sand 137sfrom origin time

对于芦山地震，从Δ1＝0km开始，按步长10km逐渐增大，直到280km时，满足在Δ1与Δ2范围内台站数量大于等于20，且3／4以上台站未限幅的条件.震中距为280—380km之间的台站位于图1中两个同心红色圆之间的环状地带，其中有17个未限幅台站，5个限幅台站.使用17个未限幅台站计算芦山地震的震级，部分台站ML随时间变化及全部台站平均ML随时间的变化如图6所示.可以看出：从初至P波到达至震后约80s（红色竖线标示位置），各台站P波最大振幅相继到达，震级急速变化；从震后80s到约137s（绿色竖线标示位置），各台站S波（或Lg波）最大振幅陆续到达，震级逐渐变大，但变化趋缓.因此，若在震后137s之前发布此次地震参数，尽管可以获取更好的时效，但却牺牲了震级的精准度，导致震级偏小.只有等到震后137s，即各台站S波（或Lg波）最大振幅到达后发布震级，此时ML达到最大值6.9，转换为标准震级为M6.8，远大于50s时所发布的标准震级M5.8，也更加接近人工正式测定的结果.

综合上述使用不同震中距范围内的台站，在不同时间点测得具有不同精准度震级的研究，以及现阶段自动速报的目的，本文认为现行的自动测定震级方法是可行的，但需要调整台站选取原则和震级发布的时间策略.对于M＜7.0的地震，需在未限幅台站占绝对优势的震中距范围内，使用未限幅记录量取ML，并作适当延时，延时到该范围最远台站的S波（或Lg波）最大振幅达到后，震级在一定时间间隔内不再变化时，再确定地震事件的震级.如此确定的震级稳定可靠，同时也在一定程度上兼顾了对时效的要求.

另外需指出的是，由于ML在7.0左右时震级会饱和，因此原则上不能使用ML测定ML≥7.0的地震.对于ML≥7.0地震震级的测定，需要使用新的震级测定方法，如下文所讨论的MWP震级测定方法.

3 MWP震级及其在芦山地震中的应用

Tsuboi等（1995，1999）发展了一种快速测定矩震级MW的方法，该方法利用宽频带地震仪记录的P波初始部分来计算标量地震矩和矩震级，能够快速得到大地震的矩震级.该方法的原理为，在均匀球状介质中，考虑在xs处的双偶极子点源激发的地震波，在xr处接收到的远场P波位移的垂直分量为

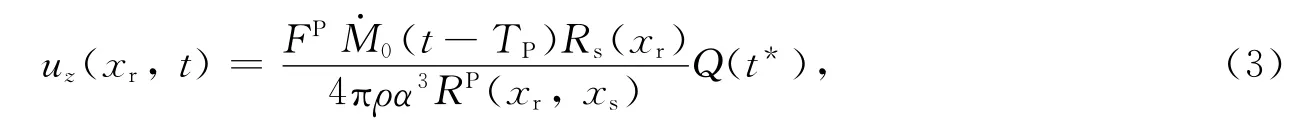
式中，FP为双偶极子震源机制确定的辐射图型，M0（t）为地震矩随时间的变化率（矩率），TP为P波走时，Rs（xr）为自由表面放大因子，RP为几何扩散因子，Q（t＊）为地震波衰减项，ρ和α分别为P波传播路径上介质的平均密度和P波平均速度.将式（3）积分得到地震矩为

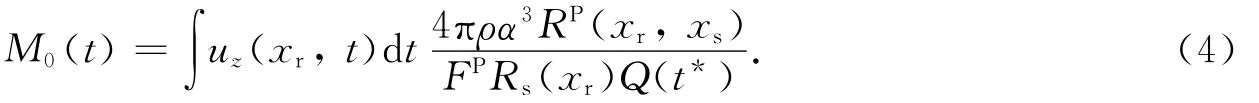
假设式（4）中M0（t）的最大值代表地震事件的地震矩，则由此可得矩震级MW.为了从实际记录的地震图中得到M0，对一些参数作了近似.取RP≈1.2r（r为震中距），Rs＝1.5，Q（t＊）≈0.8，因此从式（4）得到地震矩为

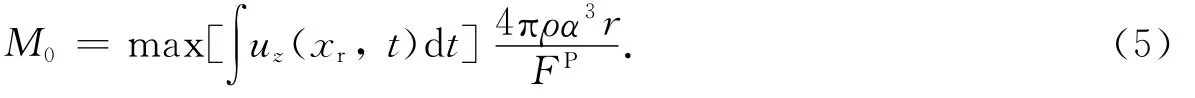
根据Tsuboi等（1995）的研究，对辐射图型进行校正，等价于平均矩震级加上0.2.为了快速得到矩震级，在计算单台矩震级时不作辐射图型校正，计算矩震级的近似值，其地震矩为

取M0为位移积分后的地震图上第一个峰值，使用标准矩震级计算公式（Kanamori，1977）

得到MW.而后将平均矩震级加上0.2，对辐射图型进行校正.该震级称为MWP（Tsuboi et al，1995），即宽频带P波矩震级.

Tsuboi等（1999）将该方法发展到可以处理深震和远震，其地震矩为

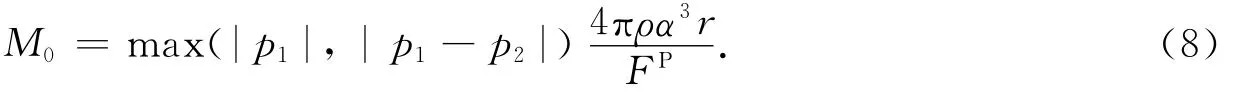
p1和p2分别为位移积分后的地震图上第一个峰值和第二个峰值.

MWP作为一种快速稳定的估计震级方法，得到了广泛应用，现已成为太平洋海啸预警中心（PTWC）、美国国家地震信息中心（NEIC）等地震自动处理系统估计震级的方法.Whitmore等（2002）研究发现，MWP与哈佛大学产出的矩震级MW有一个与震级大小有关的偏差，可通过 MWP＿cor＝（MWP＿ini－1.03）／0.843对 MWP进行校正.Kanjo等（2006）使用与震中距有关的P波速度α＝（0.16Δ＋7.9）km／s（Δ为震中距），代替计算MWP的原始公式中常数项P波速度α＝7.9km／s，提高了计算苏门答腊2004年12月26日MW9.0地震和2005年3月28日MW8.6地震的MWP准度.Tezel和Yanik（2013）使用土耳其区域台网数据计算了46次大中地震的MWP，在确定P波长度时使用了基于台站理论P波和S波到时的可变窗口.

本文在计算芦山地震MWP时，使用P波速度α＝（0.16Δ＋7.9）km／s代替P波速度α＝7.9km／s，使用［TP，TS－3］（TP和TS分别为初至P波和初至S波理论到时）作为P波时间窗，如图2中灰色框所示，并应用 MWP＿cor＝（MWP＿ini－1.03）／0.843对 MWP进行校正.在计算MWP时，在时间域从初至P波到达前10s开始到P波窗口结束，逐点计算MWP.直到初至P波到达后，才认为使用该台站计算的MWP有效.在计算全部有效MWP的算术平均值和标准差时，其误差超过标准差的值将被丢弃，重新计算剩余MWP的算术平均值，并将其作为事件最终MWP.

由于计算MWP时使用的是P波，不包括S波，因此S波或面波限幅的台站也可用于计算MWP.例如，JYA台原始记录限幅，但在所取的窗口内P波（灰色窗内的波形）不限幅（图7a）.所取的P波窗口内原始宽频带记录、位移记录、位移积分绝对值及MWP随时间的变化如图7b所示.图中红色竖线位置处取得位移积分绝对值的最大值和相应的MWP最大值，可得该台站震级MWP＝6.6.该时间即为P波时间窗结束时间，为震后27s.

对于芦山MS7.0地震，本文使用震中距320km范围内包括限幅台站在内的所有台站计算其MWP.根据Tsuboi等（1995）和Tezel和Yanik（2013）的研究认为，由于近场效应的影响，震中距太小容易导致MWP过大或过小，因此我们排除50km以内的MDS台和TQU台，用剩余的38个台计算此次地震的震级，再剔除与平均值相差1倍以上标准差的震级值，所得MWP的平均值随时间的变化关系如图8所示.可以看出：在77s之前（红色竖线标注位置，即最远台站GZI的P波时间窗截止时间），只有部分台站的波形数据满足P波时间窗，因此只有部分台站的震级是可靠的，而另外一些台站的波形数据只覆盖部分P波时间窗，位移积分绝对值可能还未达到最大，导致平均MWP较小；随着时间的推移，越来越多台站的波形数据满足P波时间窗要求，或者位移积分绝对值达到最大，平均MWP逐渐增大，直到震后77s，全部台站的位移积分绝对值达到最大，平均MWP达到最大值6.8，至此不再更新.

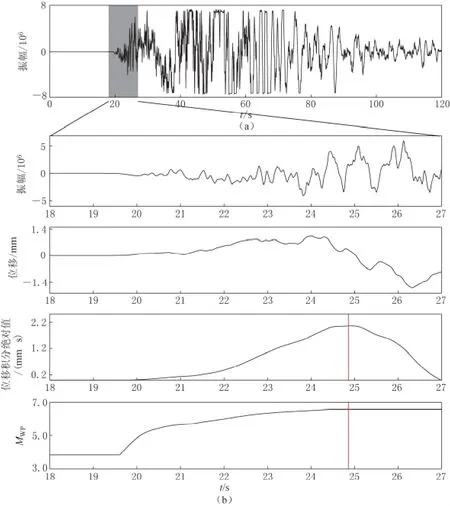
图7 JYA台由原始宽频带记录到得出MWP的处理过程（a）原始宽频带记录；（b）所取的P波窗口内原始宽频带记录、位移记录、位移积分绝对值及MWP随时间的变化Fig.7 The process from raw broadband seismogram to MWPdetermination for the station JYA（a）The raw broadband seismogram；（b）The raw broadband seismogram，displacement，the integral absolute value of displacement and MWPvariation with time within the required window of P wave

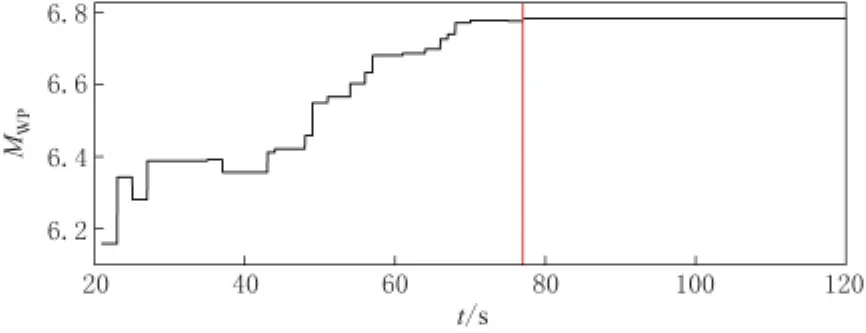
图8 平均MWP随时间的变化Fig.8 Variation of the mean MWPwith time

本文得到的震级为MWP6.8，与张勇等（2013）和王卫民等（2013）采用全球地震台网的远震地震波形数据反演得到的矩震级MW6.8和MW6.7相当一致，与全球矩心矩张量得到的矩震级MW6.6也差别不大.此外，我们还计算了中国地震台网805个可用台站的MWP，排除与平均值相差1倍以上标准差的震级值，剩余678个台站的MWP的平均值为6.7，与使用震中距320km范围内台站计算的震级相差无几，进一步说明了用区域台站资料测定MWP是可行的.

4 讨论与结论

本文通过大致还原芦山MS7.0地震自动速报系统的震级测定过程，分析了自动速报震级偏差较大的原因：一是使用了近台限幅记录，低估了震级；二是过于强调快而忽略了准.自动速报系统由于采用实时连续、不断更新的方式计算震级，不同震中距范围内台站的S波到达时间不同，如果发布地震参数过快，此时有些台站的S波（或Lg波）未到达或未完全到达，这时由于没有获取S波（或Lg波）的最大振幅，也会造成计算的震级偏小.

选取未限幅记录占绝对优势的震中距范围，使用该记录并延时到最远台站的S波（或Lg波）最大振幅到达后测定ML，既改进了测定震级的准度，同时也兼顾了对时效的要求.即使用改进的ML震级测定方法，测得ML的最大值，然而对于ML≥7.0地震还存在震级饱和问题.另外，现行的自动速报系统在发布震级时，是将测定的ML转换为标准震级M.对于标准震级M是否应该按照一个经验统计关系从ML转换得到仍存在争议，郭履灿①郭履灿.1971.华北地区的地方性震级ML和面波震级MS经验关系（全国地震工作会议资料）.得出的经验统计关系是否可用于不同地区也有待进一步研究.杨晶琼等（2013）利用云南地区地震资料，得到了该地区ML与MS之间的统计关系（MS＝1.13 ML－0.86）；汪素云等（2010）利用《中国地震年报》和《中国数字地震台网观测报告》资料，得到了中国地震台网所覆盖地区的经验统计关系（MS＝0.98 ML＋0.03）.四川芦山地区目前尚未建立ML与MS之间的统计关系，这可能也是芦山地震自动速报系统发布的震级与人工速报震级偏差较大的一个原因.

为克服ML震级饱和以及测定时不能使用近台限幅记录的制约，本文还使用了MWP震级测定方法.通过在芦山地震中的应用表明，尽管该方法是根据点源远场体波理论导出的，但仍可以应用该方法使用区域台网的波形数据在震后快速得到可靠的震级值.与ML震级测定方法相比，MWP震级测定方法有3个优点：① 由于只使用P波，因此该方法可使用S波限幅记录，大量近台资料可供使用；②当使用宽频带或甚宽频带仪器记录的波形并选取适当的P波时间窗时，震级不易饱和；③ 选取的时间窗位于S波之前，测定速度更快.另外，矩震级是目前国际主要地震监测机构优先使用的震级标度，矩震级的测定比传统震级的测定更有意义.MWP震级测定方法是对自动速报系统测定震级方法的重要补充和改进.

基于对自动测定ML震级偏差的分析与研究以及MWP震级测定方法的研究与应用，本文提出了改进目前自动速报系统测定震级的方法：①对于M＜7.0地震，用ML确定震级时，需在未限幅台站占绝对优势的震中距范围内，使用未限幅记录量取ML，并延时到最远台站的S波（或Lg波）最大振幅到达后测定ML；② 使用宽频带波形，应用MWP震级测定方法测定大地震的矩震级.

需要指出的是，尽管MWP震级测定方法以其快速稳定的优点体现出应用于自动测定震级的优势和潜力，但其也有局限性.对于大地震和特大地震，在使用MWP震级测定方法时，产出记录波形的地震仪的较窄频带和选取P波时过小的时间窗口都有可能造成对震级的低估.特别是对于M＞8.0的地震，需选择使用更宽频带（如甚宽频、超宽带）地震仪记录的波形和更远的台站.另外，对于包含多个子事件的大地震，MWP可能只代表其中一个子事件的震级，也可能导致其对震级的低估.因此，需要在未来进一步发展其它方法.

利用计算机软件自动快速测定地震参数时，误差在所难免，且自动测定与人工测定的震级类型不同，各种不同类型震级之间的转换远非一个统计关系那么简单.我们所能做的是总结经验，不断调整并改进自动测定地震参数的方法，在满足时效性要求的情况下，尽可能发布更准确的地震参数，提高中国地震局自动速报系统服务的质量和效益.

审稿专家对本文提出了宝贵意见，GMT（Wessel et al，2013）和matplotlib网站提供了软件包，作者在此一并表示感谢.

国家地震局震害防御司.1992.地震工作手册［M］.北京：地震出版社：79.

Department of Earthquake Disaster Prevention，State Seismological Bureau.1992.Earthquake Working Manual［M］.Beijing：Seismological Press：79（in Chinese）.

国家质量技术监督局.1999.地震震级的规定（GB 17740—1999）［S］.北京：中国标准出版社：1-2.

State Bureau of Quality and Technical Supervision.1999.General Ruler for Earthquake Magnitude （GB17740-1999）［S］.Beijing：China Standards Press：1-2（in Chinese）.

金星，马强，李山有.2004.利用数字化速度记录实时仿真位移与加速度时程［J］.地震工程与工程振动，24（6）：9-14.

Jin X，Ma Q，Li S Y.2004.Real-time simulation of ground displacement and acceleration using digital velocity record［J］.Earthquake Engineering and Engineering Vibration，24（6）：9-14（in Chinese）.

汪素云，王健，俞言祥，吴清，高阿甲，高孟潭.2010.基于中国地震台网观测报告的ML与MS经验关系［J］.中国地震，26（1）：14-22.

Wang S Y，Wang J，Yu Y X，Wu Q，Gao A J，Gao M T.2010.The empirical relation between MLand MSbased on bulletin of seismological observations of Chinese stations［J］.Earthquake Research in China，26（1）：14-22 （in Chinese）.

王卫民，郝金来，姚振兴.2013.2013年4月20日四川芦山地震震源破裂过程反演初步结果［J］.地球物理学报，56（4）：1412-1417.

Wang W M，Hao J L，Yao Z X.2013.Preliminary result for rupture process of Apr.20，2013，Lushan earthquake，Sichuan，China［J］.Chinese Journal of Geophysics，56（4）：1412-1417（in Chinese）.

杨晶琼，杨周胜，蔡明军，许亚吉，梁勇.2013.云南地区近震震级与面波震级转换关系研究［J］.中国地震，29（4）：513-521.

Yang J Q，Yang Z S，Cai M J，Xu Y J，Liang Y.2013.Study on the MLand MSof conversation in the Yunnan Regional Digital Networks［J］.Earthquake Research in China，29（4）：513-521（in Chinese）.

张勇，许力生，陈运泰.2013.芦山4.20地震破裂过程及其致灾特征初步分析［J］.地球物理学报，56（4）：1408-1411.

Zhang Y，Xu L S，Chen Y T.2013.Rupture process of the Lushan 4.20earthquake and preliminary analysis on the disaster-causing mechanism［J］.Chinese Journal of Geophysics，56（4）：1408-1411（in Chinese）.

中国地震局.2001.地震及前兆数字观测技术规范［M］.北京：地震出版社：64.

China Earthquake Administration.2001.Specification for Seismic and Precursor Digital Observation Techniques［M］.Beijing：Seismological Press：64（in Chinese）.

Allen R M，Kanamori H.2003.The potential for earthquake early warning in southern California［J］.Science，300（5620）：786-789.

Allen R M，Ziv A.2011.Application of real-time GPS to earthquake early warning［J］.Geophys Res Lett，38（16）：L16310.

Delouis B，Charléty J，Vallée M.2009.A method for rapid determination of moment magnitude MWfor moderate to large earthquakes from the near-field spectra of strong-motion records（MWSYNTH）［J］.Bull Seismol Soc Am，99（3）：1827-1840.

Earthworm.2011.Earthworm modules：Localmag overview［EB／OL］.［2013-05-15］.http：∥www.earthwormcentral.org／documentation2／ovr／localmag＿ovr.html.

Hara T.2007.Magnitude determination using duration of high frequency energy radiation and displacement amplitude：Application to tsunami earthquakes［J］.Earth Planets Space，59（6）：561-565.

Kanamori H.1977.The energy release in great earthquakes［J］.J Geophys Res，82（20）：2981-2987.

Kanjo K，Furudate T，Tsuboi S.2006.Application of MWPto the great December 26，2004Sumatra earthquake［J］.Earth Planets Space，58（2）：121-126.

Katsumata A，Ueno H，Aoki S，Yoshida Y，Barrientos S.2013.Rapid magnitude determination from peak amplitudes at local stations［J］.Earth Planets Space，65（8）：843-853.

Lomax A，Michelini A，Piatanesi A.2007.An energy-duration procedure for rapid determination of earthquake magnitude and tsunamigenic potential［J］.Geophys J Int，170（3）：1195-1209.

Lomax A，Michelini A.2009.MWPd：A duration-amplitude procedure for rapid determination of earthquake magnitude and tsunamigenic potential from P waveforms［J］.Geophys J Int，176（1）：200-214.

Saul J，Bormann P.2007.Rapid estimation of earthquake size using the broadband P-wave magnitude mB［EB／OL］.［2013-05-15］.ftp：∥ftp.gfz-potsdam.de／pub／home／st／saul／SaulBormannPosterAGU2007.pdf.

SeisComp3.2013.SeisComp3［EB／OL］.［2013-05-15］.http：∥www.seiscomp3.org／wiki／doc／applications／scmag.

Tezel T，Yanik K.2013.Improvement in MWPmagnitude determinations and applications to earthquakes in Turkey［J］.Seismol Res Lett，84（6）：991-996.

Tsuboi S，Abe K，Takano K，Yamanaka Y.1995.Rapid determination of MWfrom broadband P waveforms［J］.Bull Seismol Soc Am，85（2）：606-613.

Tsuboi S，Whitmore P M，Sokolowski T J.1999.Application of MWPto deep and teleseismic earthquakes［J］.Bull Seismol Soc Am，89（5）：1345-1351.

Vallée M，Charléty J，Ferreira A M G，Delouis B，Vergoz J.2011.SCARDEC：A new technique for the rapid determination of seismic moment magnitude，focal mechanism and source time functions for large earthquakes using bodywave deconvolution［J］.Geophys J Int，184（1）：338-358.

Wessel P，Smith W H F，Scharroo R，Luis J，Wobbe F.2013.Generic Mapping Tools：Improved version released［J］.EOS Trans AGU，94（45）：409-410.

Whitmore P M，Tsuboi S，Hirshorn B，Sokolowski T J.2002.Magnitude dependent correction for MWP［J］.Sci Tsunami Hazards，20（4）：187-192.

Wu Y M，Teng T L.2002.A virtual subnetwork approach to earthquake early warning［J］.Bull Seismol Soc Am，92（5）：2008-2018.

Wu Y M，Yen H Y，Zhao L，Huang B S，Liang W T.2006.Magnitude determination using initial P waves：A singlestation approach［J］.Geophys Res Lett，33（5）：L05306.

Wu Y M，Kanamori H，Allen R M，Hauksson E.2007.Determination of earthquake early warning parameters，τcand Pdfrom southern California［J］.Geophys J Int，170（2）：711-717.

Yamada T，Ide S.2008.Limitation of the predominant-period estimator for earthquake early warning and the initial rupture of earthquakes［J］.Bull Seismol Soc Am，98（6）：2739-2745.

Yamada M，Mori J.2009.Usingτcto estimate magnitude for earthquake early warning and effects of near-field terms［J］.J Geophys Res，114（B5）：B05301.

Zollo A，Lancieri M，Nielsen S.2006.Earthquake magnitude estimation from peak amplitudes of very early seismic signals on strong motion records［J］.Geophys Res Lett，33（23）：L23312.