*基于节理网络模拟和分形理论预测矿岩体块度
杨 啸,杨志强,2,高 谦,薛改利(.北京科技大学金属矿山高效开采与安全教育部重点实验室,北京00083;2.金川集团股份有限公司,甘肃金昌73700)
*基于节理网络模拟和分形理论预测矿岩体块度
杨 啸1,杨志强1,2,高 谦1,薛改利1
(1.北京科技大学金属矿山高效开采与安全教育部重点实验室,北京100083;2.金川集团股份有限公司,甘肃金昌737100)
摘 要:块度尺寸和分布特征是自然崩落法选择与设计的重要依据之一,块度预测的可靠性决定采矿方法设计的成败。以金川镍矿Ⅲ矿区贫矿自然崩落采矿法可行性研究为工程背景,开展了岩体块度预测研究;根据Ⅲ矿区开拓工程所揭示的工程岩体,进行了3个区域的岩体节理裂隙调查与统计分析,获得了节理裂隙统计结果及空间分布特征参数;采用蒙特卡罗随机模拟方法生成节理网络模型,并结合岩体分形理论,推导出矿岩体块度尺寸与分布的预测模型;基于所建立的预测模型进行矿岩体初始块度预测。结果表明,当特征尺寸确定为1.2m时,根据1 570m中段调查的4个区域的矿岩体大块率分别达到8.8%,20%,14.83%,6.51%,平均大块率为12.54%;虽然Ⅲ矿区矿岩体破碎,但矿石比岩石强度高,导致矿岩体初始块度的大块率较高,不利于自然崩落法的放矿控制和连续生产。本研究结果为金川矿山的采矿方法选择与决策提供了理论依据。
关键词:自然崩落采矿法;节理网络模拟;蒙特卡罗方法;岩体分形理论;初始块度预测
(E-mail)sendeyouxiang@163.com
通讯联系人:高谦,男,教授,博导,主要从事充填采矿和地压控制技术研究,(E-mail)gaoqian@ces.ustb.edu.cn
自然崩落法是一种大规模和低成本的采矿方法,自1895年在美国试验成功以来,迄今已有100多年的历史。因其生产能力大,开采成本低,安全性好,便于生产组织管理,是唯一能与露天开采经济效益相媲美的高效率地下采矿方法,备受各国采矿工作者青睐[1-2]。自然崩落法的选择与应用,矿石的可崩性、崩落矿石块度以及底部结构的稳定性是3个关键因素。在生产过程中,矿石崩落块度的分布决定了大块产出率及二次破碎方法和炸药消耗量、矿石流动性以及对放矿过程的控制[3]。如果块度不能满足设计放矿的要求,势必影响矿石出矿能力以及二次处理对底部结构稳定性影响,难以达到预期的生产能力和经济效益。因此,矿石块度的准确预测对自然崩落法应用的成功与否具有重要影响。
显然,矿石块度主要取决于矿岩体节理密度、产状以及节理条件。因此,人们开展了基于节理切割岩体形成块体来预测矿岩块度。Amitabha Mukherjee和Ashraf Mahtab引入节理持续性系数及有效间距的概念,建立二维模型对块度分布进行研究,由此揭示了节理的持续性、节理间距等因素对其影响;赖顺华和童光旭[4]运用编制的节理岩体计算单元生成程序,建立了块度预测的二维模型,进而研究了崩落矿石的块度及组成;王家臣[5-6]等运用蒙特卡罗随机模拟方法生成三维节理网络,并运用拓扑学中的单纯同调理论对矿石块度进行预测;王李管[7-9]等采用三维矿岩块度预测软件MAKE BLOCK,定量分析矿石块度影响因素,从而对矿石块度分布进行预测和分析;王利和高谦[10-11]根据岩石分形断裂切割岩块的块度形成机理,利用能量守恒关系,建立了损伤-能量-碎块尺寸理论关系式。
笔者以金川大型铜镍矿床Ⅲ矿区的贫矿开采为对象,开展自然崩落法应用于该矿的可行性与可靠性研究。首先根据现场节理裂隙调查结果,按照地质统计学统计其空间分布特征参数[12];然后,采用蒙特卡罗(Monte Carlo)随机模拟方法生成的节理网络模型和RQDt节理岩体预测原理,以及岩体分形理论推导出的块度预测模型,由此对Ⅲ矿区的矿岩体初始块度进行预测和分析,为该矿山贫矿开采的采矿方法选择提供理论依据。
1 节理网络模拟与块度预测
节理裂隙在空间上的相互切割,构成了岩体初始块度集合体。同时,大量理论与实践研究结果表明,在工程应力水平下,岩体尤其是坚硬矿体的破坏主要是沿原生节理面发展贯通,完整岩块很难破裂。因此,节理发育程度往往决定了矿岩体块度分布规律。所以,节理裂隙的调查与统计分析是进行矿岩体块度预测的基础。
为了获得Ⅲ矿区矿岩体的节理分布,在已经掘进的多条巷道,开展节理裂隙调查与节理裂隙统计分析。图1所示为该矿矿岩体节理极点分布图和极点等密图。利用Schmidt投影法对数据综合处理,最终将其划分成4个主要的节理组。

图1 Ⅲ矿区矿岩体极点分布图和极点等密图Fig.1 Pole distribution and iso-intensity diagram
1.1 蒙特卡罗随机模拟原理
节理网络模型预测是在现场节理调查和统计分析的基础上,建立节理面几何参数的概率统计模型,进而运用蒙特卡罗随机模拟原理和方法,求得表征节理面分布特征的节理网络图像。随机模拟程序原理如图2所示。
运用蒙特卡罗(Monte Carlo)随机模拟时,引用如下假设:
1)在给定的模拟区域内,节理中心的空间分布服从泊松分布;
2)将零散节理视为均匀分布,即在区域内出现的概率是相等的;
3)二维模型网络中的直线段代表节理迹线,其产状由方向角唯一确定,即自X轴逆时针旋转至迹线的角度;
4)节理面空间几何参数(倾角、倾向、间距及迹线持续长度等)服从均匀、正态和负指数分布规律中的一种[13];
5)节理条数由单位面积的节理中心数目定义,节理张开度(隙宽)服从对数正态分布。
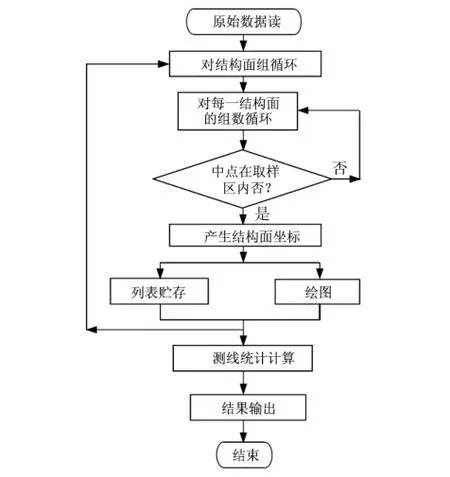
图2 程序原理框图Fig.2 Program principle flow chart
1.2 节理网络的生成
笔者仅对Ⅲ矿区南风井23点穿脉工程进行节理网络模拟与分析。首先,在用DIPS软件生成的节理等密度图和节理玫瑰图基础上,按倾角对节理进行分组;其次,对每组的倾角、迹长、段距、间距等节理参数进行统计分析,确定其概率分布形式和相应的数字特征,包括均值和方差(如表1所示)。

表1 节理参数统计表Table 1 Statistical parameters of joints
最后,根据蒙特卡罗法生成节理统计结果,将相应的参数输入计算机进行模拟,可以得到节理系统和空间某平面的交线段,平面内的这些线段组成该平面内的节理网络模拟图,如图3所示。
现场观测到的数据是真实的三维空间节理面与暴露面的交割线,无法反映空间节理面在矿体内的真实分布情况,所以,笔者采用比较简便和成熟的圆盘模型。在建立节理网络模型时,将线密度和面密度转化为体密度,从而得到由节理面在岩体中的交接和切割所构成的岩块大小和形状的分布组成。此外,不仅采用了优势节理组,而且考虑到了零散节理的分布,体现了节理网络模拟的优势。

图3 节理网络模拟图Fig.3 Joint network simulation diagram
1.3 基本预测原理
RQD是Deer于1964年提出的,用于评价岩体块度(完整性)的指标,表示长度在10cm(含10cm)以上的岩芯,累计长度占钻孔总长度的百分比。通过引进阈值提出广义的RQD,即对任一间距阈值t,沿某一测线方向大于t的间距之和与测线总长之比的百分数,用Z表示。其基本原理是,在计算机程序生成的节理网络模拟图窗口内布置测线,然后在测线上测量节理面的间距,进而计算Z值。
为了消除单方向布置测线所造成的误差,笔者采用全方位布置测线的方法,图4为测线布置图。其中,实线代表节理网络模拟的节理面,虚线代表布置的测线。在测线布置图中,只示意了在窗口的底边和窗口左侧边上某一个点布置的测线,在实际运作过程中窗口的4个边都可以布置很多的点,测点的密度可以根据需要确定,每一个测点可以一定的角度放射出测线,测线的角度可以根据需要予以控制,每一条测线都可以获取该测线上的Z值。
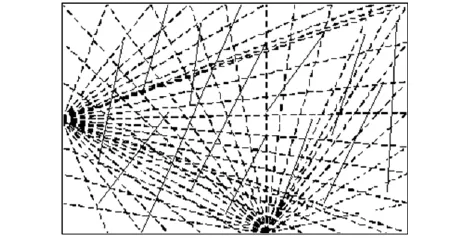
图4 测线布置图Fig.4 Survey lines layout diagram
设,窗口底边从左向右为X轴正向,窗口左侧边从下向上为Y轴正向。根据起始点坐标和测线角度,分别建立各个节理面和测线的解析方程。
测线的解析方程:
YS,K,α=α(XS,K,α-XS,K)+YS,K.(2)
式中:D为节理面;I为节理面的序数;S为测线;K为测线的序数;α为测线与X轴正向之间的夹角。1.4 预测结果分析
根据风井23点穿脉节理网络模拟图的生成过程,分别求得第三条穿脉上盘沿脉和下盘沿脉的节理网络模拟图;然后,根据公式(1)和(2),求解每一条测线与各节理面方程的交点,计算出各交点间的距离,即得到该测线上节理面的间距。当给出不同的阈值时,可以求取所对应的Z值及其分布图。表2为基于不同阈值t的Z块度预测结果,图5为风井23点穿脉Z值分布图。

表2 基于不同阈值t的Z块度预测结果Table 2 Results of Zfragmentation prediction based on different threshold

图5 风井23点穿脉Z值分布图Fig.5 Distribution of shaft 23point vein Z value
由表2可知,风井23点穿脉和下盘沿脉的Z值小于第三条穿脉和上盘沿脉的Z值,说明后者岩体质量相对较好。特别是风井23点穿脉和下盘沿脉区,虽然0.1m块径的Z值较高,但大块径的Z值很低,最小值仅0.065 1,矿区岩体质量较差。此外,如果大于某一特征尺寸的比例称为大块率,当特征尺寸定为1.2m时,在1 570m中段调查的4个区域初始块度均存在大块,其大块率分别为8.8%,20%,14.83%,6.51%,平均大块率12.54%。矿区节理间距较小,节理密度较大,且由Z分布图上可以看出,岩体各向异性明显,矿岩体的完整性较差。
2 基于岩体分形理论的块度预测
2.1 基本预测原理
用分形维数可以表示看似杂乱无章的块度分布,恰当地反应了岩石破碎程度的统计特征[14]。同时在一定的测度条件下,裂隙的分形几何维数与块度分布的分形维数相等。因此,可以根据裂隙的分形模型来推导矿岩体初始块度的预测模型。
矿岩体的块度分布函数有很多形式,地质学中广泛应用具有代表性的是R-R和G-G-S分布。其中G-G-S分布函数为:式中:Y为块度小于x的累积相对量;x为岩石块度(筛网孔径);n为分布参数;x0为平均大块尺寸。
用m(t)表示岩块的总质量,m(r)表示特征尺寸为r的筛下累积量,则式(3)转化为:筛上累积量为
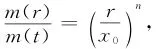

令,Db为块度分布的分形维数,则特征尺度大于或等于r的碎块数N:对公式(4)和(5)进行微分,可以得出:


设,节理密度为λ,x0=1/λ,对应块度x的筛网孔径用t表示。当取不同的界限值t时,x/x0=λt,将其与式(6)代入到式(3),则有岩体节理密度的分形维数与岩体块度累积量的关系:将一系列的λt和Y投影到log(λt)和logY的坐标图上,得到一系列的点,在图上找出无标度区,用最小二乘法可以获得如下的拟合曲线:通过改变不同块度尺寸t值,可以预测出矿块岩体的初始块度。


由于只考虑节理裂隙对矿岩体的切割作用,并未涉及采矿诱导应力导致岩体沿节理追踪破坏和发生碰撞导致的岩石破碎。因此,基于岩体分形理论获得的预测模型,仅限于预测初始块度分布。
2.2 预测结果分析
根据金川镍矿Ⅲ矿区有限的开拓工程所获得的节理裂隙调查结果,进行节理统计分析和分形维数(分形维数均属于合理范围[15]1.43~2.10)计算,由此获得苏喷调查的工程岩体节理参数和相应的岩体质量评价(见表3)。
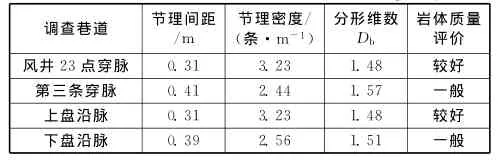
表3 岩体质量评价结果Table 3 Evaluation results of rock mass quality
在此基础上,利用岩体分形理论进行矿岩块度预测,由此获得了基于巷道节理调查的矿岩体的块度预测结果(见表4)。
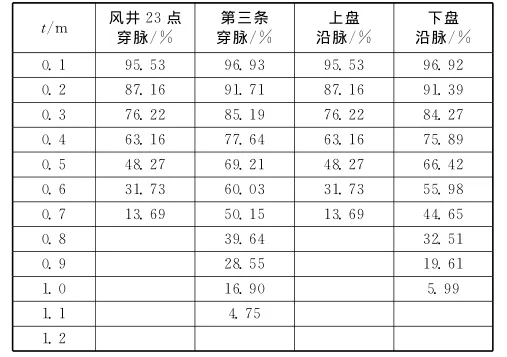
表4 矿岩块度预测结果Table 4 Results of rock fragmentation prediction
由表4可以看出,如果将特征尺寸定为1.2m时,调查的4个区域均没有大块的出现。显然,矿岩体初始块度的大块率较小,一般情况下不会存在大块问题。
3 结论
矿岩体块度的准确预测是自然崩落法设计的关键技术。基于节理网络模拟和岩体分形理论,对矿岩体初始块度进行预测研究,得出以下结论:
1)节理裂隙在空间上的相互交接和切割,构成了矿岩体初始块度的集合体;
2)基于蒙特卡罗方法生成的节理网络模型,采用了优势节理组以及零散节理分布进行预测,能够较真实地反应初始块度分布;
3)由Z分布图可以看出,矿岩体各向异性明显,且完整性较差;
4)基于岩体分形理论推导出的预测模型,只考虑节理裂隙对矿岩体的切割作用,因此仅能预测初始块度分布;
5)当矿块特征尺寸定为1.2m时,节理网络模拟结果表明,在1 570m中段调查的4个区域初始块度均存在大块,其大块率分别为8.8%,20%, 14.83%,6.51%,平均大块率为12.54%。因此,金川镍矿Ⅲ矿区的自然崩落法采矿设计,应考虑矿岩体初始大块率对自然崩落法采矿的影响。
参考文献:
[1] 陈清运,蔡嗣经,明世祥,等.国内自然崩落法可崩性研究与应用现状[J].矿业快报,2005,21(1):1-4.
[2] 沈南山,顾晓春,尹升华.国内外自然崩落采矿法技术现状[J].采矿技术,2009,9(4):1-4,15.
[3] 董卫军.矿石崩落块度的三维模型与块度预测[J].矿冶,2002,11(2):1-3,25.
[4] 赖森华,童光煦.节理岩体计算单元生成与崩落块度预测[J].有色金属:矿山部分,1988(3):17-22.
[5] 王家臣,陈忠辉,熊道慧,等.金川镍矿二矿区矿石自然崩落规律研究[J].中国矿业大学报,2000,29(6):596-600.
[6] 王家臣,熊道慧,方君实.矿石自然崩落块度的拓扑研究[J].岩石力学与工程学报,2001,20(4):443-447.
[7] 王李管,尚晓明,冯兴隆,等.基于Monte Carlo模拟的矿岩块度预测[J].煤炭学报,2008,33(6):635-639.
[8] 冯兴隆,王李管,毕林,等.矿石崩落块度的三维建模技术及块度预测[J].岩土力学,2009,30(6):1826-1830.
[9] 李响,贾明涛,王李管,等.基于蒙特卡罗随机模拟的矿岩崩落块度预测研究[J].岩土力学,2009,30(4):1186-1190.
[10] 王利,高谦.岩石块度的分形演化模型及其应用[J].煤炭学报,2007,32(11):1170-1174.
[11] 王利,高谦.基于损伤能量耗散的岩体块度分布预测[J].岩石力学与工程学报,2007,26(6):1202-1211.
[12] 侯景儒,郭光裕.矿床统计预测及地质统计学的理论与应用[M].北京:冶金工业出版社,1993.
[13] 赵文广.节理随机概率模型应用于块体理论的研究[D].沈阳:东北工学院,1991.
[14] 高峰,谢和平,赵鹏.岩石块度分布的分形性质及细观结构效应[J].岩石力学与工程学报,1994,13(3):240-246.
[15] 谢和平.分形-岩石力学导论[M].北京:科学出版社,1997:228-234.
(编辑:庞富祥)
Block Size Prediction of Rock Masses Based on Joint Network Simulation and Fractal Theory
YANG Xiao1,YANG Zhiqiang1,2,GAO Qian1,XUE Gaili1
(1.Key Laboratory of High Efficient Mining and Safety for Metal Mine of Ministry of Education,
University of Science and Technology Beijing,Beijing100083,China;2.Jinchuan Group Co.Ltd.,Jinchang737100,China)
Abstract:Integration of size and distribution characteristic of block is the important basis of selection and design with natural caving method,and reliability of block prediction is decisive for success of mining method design.On the background of feasibility research of natural caving mining method for lean ore of Jinchuan Nickel ore III District,rock block prediction research is conducted.First,according to engineering rock revealed by development engineering of III District,rock joint fissure survey and statistic analysis of three fields were conducted,thus,obtaining joint fissure statistical results and space distribution characteristics parameters;then,generating joint network model with Monte-Carlo random simulation method,and deducing prediction model of rock masses block size and distribution combining with rock fractal theory;last,conduct rock block initial prediction based on the prediction model developed.It turned out that,when the characteristic size is determined as 1.2m,rock masses boulder yield of four fields surveyed according to middle 1570mis 8.8%,20%,14.83%and 6.51%respectively,average at 12.54%,which shows that,although rock masses of III District is broken,ore and rock are of high intensity,and intensity of ore is higher than that of rock,resulting in high boulder yield of rock masses initial block,adverse to ore drawing control and process production with natural caving method.The research results provide theoretical basis for mining method selection and decision-making of Jinchuan mines.
Key words:natural caving mining method;joint network simulation;monte carlo method;rock fractal theory;initial block size prediction
作者简介:杨啸(1988-),男,河南郑州人,博士生,主要从事矿山岩石力学与采场地压控制技术研究,(Tel)13811115638,
基金项目:国家重点基础研究发展计划:重大工程地质灾害的预测理论及数值分析方法研究(2010CB731500)
收稿日期:*2014-11-05
文章编号:1007-9432(2015)03-0318-05
DOI:10.16355/j.cnki.issn1007-9432tyut.2015.03.014
文献标识码:A
中图分类号:TD852

