齿啮式卡箍连接件的接触分析

李春涛 王慧玲 周伟光

（中航黎明锦西化工机械（集团）有限责任公司 葫芦岛 125001）

齿啮式卡箍连接件的接触分析

李春涛 王慧玲 周伟光

（中航黎明锦西化工机械（集团）有限责任公司 葫芦岛 125001）

利用ANSYS软件进行接触分析解决特殊形式的齿啮式卡箍连接件的强度计算问题，重点讲述软件相关参数的设置，并对比相关参数变化对计算结果的影响，同时对各种接触算法进行比较。

齿啮式卡箍连接件 ANSYS 接触分析

齿啮式卡箍连接件是快开门式压力容器上的快速密封锁紧装置，通过相互嵌套的封头齿和卡箍齿的错开和啮合实现压力容器的快速开启。齿啮式卡箍连接件的计算方法，系参照JIS B8284《压力容器快速开闭装置的设计》而制定的[2]。该计算方法适用于两种典型的结构：非整体齿啮式卡箍连接件和整体齿啮式卡箍连接件，如图1和图2所示。

目前，许多行业所用的快开门压力容器在结构上不能完全符合文献[2]计算方法的要求，最常见的就是带凸形封头的齿啮式卡箍连接件，如图3所示。对于这类齿啮式卡箍连接件，使用有限元软件进行应力分析并按分析设计标准进行应力评定是目前最主要的设计方法。

图1 非整体式

图2 整体式

图3 带凸形封头的齿啮式卡箍连接件

1 齿啮式卡箍连接件的有限元分析

在对齿啮式卡箍连接件进行有限元分析时，最常用的方法是把封头、卡箍和下法兰分别单独建模并分析计算。球冠形封头和上法兰组成一个整体，在上法兰与卡箍的压紧面处施加轴向约束来模拟卡箍对上法兰在轴向方向的限制作用。卡箍和下法兰则分别在各自的压紧面根据轴向力平衡施加均布的等效力。

这种计算方法，把原本协同受力的元件分离成单个模型，认为元件之间的接触面是彼此完全贴合的，并且假设在压紧面上的等效力是均布的。法兰齿与卡箍齿之间的接触面不仅相互挤压，而且相对滑动，因此，齿间的接触摩擦问题也是需要考虑的因素[3]。综上所述，把各个部件单独建模并分析的方法，不能最大限度地真实反映出结构在实际承载时的受力情况。

随着国内有限元分析计算水平的提高，齿啮式卡箍连接件越来越多地采用有限元接触分析进行计算，文献[3]详细叙述了采用ANSYS软件的接触单元模拟齿间啮合的接触过程，建立了基于整体有限元应力分析和应力分类的接触分析计算方法。接触分析计算方法，在建模时把整个结构在一个模型中建出，利用ANSYS软件提供的接触单元，把法兰齿与卡箍齿之间的压紧面定义成一组接触对，并考虑齿间的摩擦，用非线性接触分析来模拟结构中各个元件之间的相互作用。这种计算方法，减少了近似的假设，考虑了齿间的摩擦滑动，而且，接触问题本身就是一个高度非线性的问题，采用非线性的接触分析计算方法显然更加合理。

2 齿啮式卡箍连接件的接触分析

采用接触分析，虽然更加合理和真实地模拟了结构的实际行为，但在接触分析过程中，涉及到接触单元的实常数和关键选项的设置，这些设置对计算结果的正确性、合理性起到至关重要的作用，同时也常常使工程技术人员感到困惑。因此本文将结合带凸形封头的齿啮式卡箍连接件，详细讲述在使用ANSYS软件进行接触分析时，一些主要实常数和关键选项的设置，并通过一些计算结果的对比来说明这些设置的物理意义及对于结果的影响。

有限元模型如图4所示。利用结构的周期对称性，建立结构的1/32（齿数16）模型。在模型完成实体单元划分后，将上法兰齿的压紧面指定为接触面，将卡箍齿的压紧面指定为目标面，并指定相同的实常数号，然后在上法兰和卡箍的压紧面上分别生成接触单元和目标单元。ANSYS程序将通过这一实常数号来识别接触对。

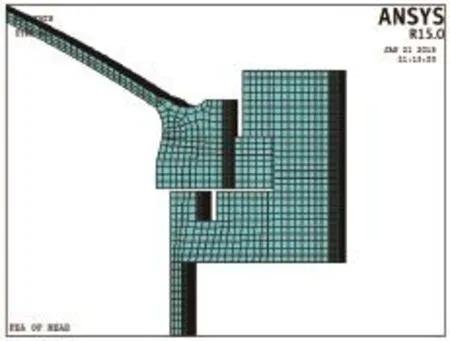
图4 有限元模型

由于上封头部分仅仅通过接触的出现来约束刚体运动，因此在建模时要保持上封头和卡箍的压紧面保持独立且无间隙。即使实体模型在初始时处于接触状态，在网格划分后由于数值舍入误差，两个面的单元网格之间也可能会产生小缝隙。在ANSYS程序中设置接触单元的关键选项KEYOPT（5）=3，使ANSYS能够自动提供实常数CNOF值到刚好闭合间隙，这样上封头就不会出现刚体运动（接触单元的实常数CNOF用于指定施加于接触面的正或负的偏移值）。

关于摩擦问题，首先要把接触面相对滑动的摩擦系数定义为一个材料的属性，并在创建接触对时指定为接触单元的材料。其次，ANSYS程序提供了一个人为指定最大等效剪应力的选项，不管接触压力值的大小，如果等效剪应力达到此值时，即发生滑动。为了指定接触截面上最大容许剪应力，设置实常数TAUMAX，一个合理的上限估值为σs/30.5（σs是材料的屈服强度）。

完成上述设置并加载之后，其他实常数及关键选项均采用ANSYS程序的默认值，即可得出计算结果。但对于这个计算结果，要分析结构的接触刚度和穿透值是否在一个相对合理的范围内。

3 接触刚度和允许穿透值对分析结果的影响

ANSYS程序默认使用增进拉格朗日乘子法，增进拉格朗日乘子法是为了找到精确的拉格朗日乘子（即接触力）而对罚函数进行一系列修正迭代。在迭代的开始，接触协调条件基于惩罚刚度决定，一旦达到平衡，就检查许可穿透量。这时，如果有必要，接触压力增大，继续进行迭代。

使用实常数FTOLN来指定允许的最大穿透。接触单元的实常数FTOLN是基于单元厚度的一个系数，用于计算允许的穿透。ANSYS程序根据接触单元的材料特性，来估计一个缺省的接触刚度。对面面接触单元CONTA174，可以用实常数FKN来为接触刚度指定一个比例因子或指定一个绝对值。比例因子一般在0.01和10之间。对于大变形问题，选1是比较好的；而对于弯曲为主的问题，通常为0.01~0.1。

接触刚度在接触力与接触面间的穿透值（接触位移）之间建立起力与位移的线性关系：接触刚度x接触位移=法向接触力。

在程序中通过分离的接触体上节点间的距离来计算穿透值。接触刚度越大，穿透值就越小，理论上在接触刚度为无穷大时，可以实现完全的接触状态，使穿透值等于零。但是显而易见，在程序计算中，接触刚度不可能为无穷大（否则病态），穿透也就不可能真实达到零，而只能是个接近于零的有限值。

综上所述，既能使计算收敛，而又能使穿透值达到可接受的最小值，这是我们调整接触单元相关实常数的基本原则。在这个原则的指导下，调整相关实常数进行多次试算，对计算结果进行对比和分析。当不断增大接触刚度时，每次计算结构中的最大应力最终应逐渐趋于一个稳定的数值。这样，就可以确定一个较好的接触刚度和较为合理的穿透值，计算结果也是能够接受的。

4 接触分析计算结果

为了确定接触刚度和允许穿透值对分析结果的影响，结合与图3所示结构相似的设计实例，设置不同的接触刚度比例因子和允许穿透比例因子并对相应计算结果进行对比和分析，计算软件使用ANSYS15.0。其中，设计参数见表1，软件参数设置（其他设置可参照文献[5]）见表2，计算结果见表3，表4。

表1 设计参数

表2 软件参数设置

4.1 计算结果

1）设置不同的接触刚度比例因子（0.1~10），实常数FTOLN=0.1（默认值）。

表3 计算结果

2）根据1）的计算结果中的穿透值，且考虑到FTOLN是基于单元厚度的一个系数（本例中单元厚度为5mm），调整实常数FTOLN=0.1E-03。

表4 计算结果

3）把上述计算结果绘制成曲线见图5。

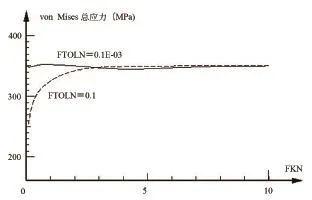
图5 根据计算结果绘制的曲线

4.2 结果分析

总体来说，当增加接触刚度比例因子时，使von Mises总应力不断增加并且趋于稳定值，穿透值单调减小。当改变允许穿透值时，即使在接触刚度比例因子较小时，von Mises总应力也与稳定值相差不到1%，且随着接触刚度比例因子的增大，总应力很快地逼近稳定值。

4.3 应力评定

在齿啮式卡箍连接件的上下法兰齿根部处设定路径进行线性化处理，薄膜应力及薄膜加弯曲应力随接触刚度比例因子和实常数FTOLN的变化很小，同时，高于单独建模并分析计算方法的计算结果。因此，后者的计算方法偏于不安全，应尽量避免使用。应力线性化和结果评定请读者参照文献[3]进行。

5 与其他接触算法的比较

对于CONTA174接触单元，目前版本的ANSYS除了本文第3章介绍的增进拉格朗日接触算法，还提供了另外4种接触算法：罚函数法、多点约束（MPC）法、法向拉格朗日乘子法+切向罚函数法、纯拉格朗日法。

增进拉格朗日乘子法中包含和应用了罚函数法，相比单纯的罚函数法，可能迭带次数会更多，但在接触问题的求解控制中可以有更多、更灵活的控制，可以更快地实现一个需要的穿透极限。

增进拉格朗日乘子法的穿透并不是零，但增进拉格朗日乘子法：较少病态，接触单元的接触刚度取值可能更合理；与单纯的拉格朗日法相比，没有刚度阵零对角元；在选择求解器上没有限制，PCG等迭代求解器都可以应用；用户可以自由控制允许的穿透值TOLN；可以避免法向拉格朗日乘子法+切向罚函数法所产生的震荡。

法向拉格朗日乘子法+切向罚函数法不是采用力与位移的关系来求接触力，而是把接触力作为一个独立自由度。因此这里不需要进行迭代，而是在方程里直接求出接触力（接触压力）来。从而，拉格朗日乘子法不需要定义人为的接触刚度去满足接触面间不可穿透的条件，可以直接实现穿透为零的真实接触条件，这是罚函数法所不可能实现的。一个可能发生的严重问题，就是在接触状态发生变化时，例如从接触到分离，从分离到接触，此时接触力有个突变，产生震荡 chattering（接触状态的振动式交替改变）。

多点约束（MPC）法使用内部生成的约束方程在接触面上保证协调，接触节点的自由度被取消，不需要法向和切向刚度，对小变形问题求解平衡方程时不需迭代，因此计算时间很短。

用MPC法计算本例，von Mises总应力为346.3MPa，与本文4.4 2）节中使用增进拉格朗日乘子法（FKN=10）时的计算结果非常接近，但运算时间缩短约2/3。

通过应力线性化，发现法兰齿根部的薄膜应力及薄膜加弯曲应力低于增进拉格朗日乘子法的计算结果很多。对比一下两种计算方法的应力云图，见图6~图7，MPC法使上下法兰齿压紧面始终接触，相当于增加了法兰齿的刚度，导致变形量偏小，因此不太适用本例的计算。

Contact-analysis of Tooth-locked Clamp Connecting Fittings

Li Chuntao Wang Huiling Zhou Weiguang
(AVIC Jinxi Chemical Machinery（Group）Co., Ltd. Huludao 125001)

Using ANSYS software to deal with the contact-analysis of tooth-locked clamp connecting fittings, the emphasis of this article is how to configure parameter of ANSYS software during contact-analysis, and the author have compared the effecting caused by parameter changing and various kinds contact algorithm within ANSYS software.

Tooth-Locked clamp connecting fittings ANSYS Contact-analysis

X933.4

B

1673-257X(2015)09-0066-04

10.3969/j.issn.1673-257X.2015.09.015

李春涛(1975～),男，本科，高级工程师，主要从事压力容器设计工作。

2015-03-31）